基于机器视觉几何特征参数的大蒜根部尺寸预测

郭 烽， 赵鹏飞， 王福明， 孙志青， 赵青杨， 赵重鹏， 吴江雪

(中北大学 机械工程学院， 山西 太原 030051)

0 引 言

中国大蒜出口国际市场的占有率接近80%， 但大多以初级商品为主， 加工程度低， 导致出口产品价格低廉[1]， 加大大蒜产品的深加工是大蒜产业发展的必然趋势. 切须工艺是出口大蒜产品的深加工工序中的关键步骤， 目的是在切除蒜须的同时， 尽可能减少大蒜果实部分的损失. 由于大蒜形态各异， 目前大蒜自动化加工无法完全切除蒜胡(蒜须的根部)， 依然需借助人工才能彻底去除大蒜的根须. 因此， 实现大蒜蒜胡形状尺寸的无损精确预测对自动化切须具有重要意义.

近年来， 机器学习广泛应用于农业中的分类识别和回归预测， 为工程应用提供更为准确的农业数据， 极大地提高了生产效率， 降低了劳动成本[2-3]. 宋彦等[4]提出了一种基于形状特征直方图结合支持向量机的茶叶等级识别方法， 通过提取叶片的6个形状特征， 建立SVM预测模型， 识别精度达到95.71%. Sun等[5]提出了一种凸点匹配方法来分离粘附的稻米粒， 并使用支持向量机计算垩白度的位置和程度， 从而确定水稻垩白度的类型. 郭澎涛等[6]利用高光谱技术结合BP神经网络模型对橡胶苗叶片磷含量进行预测， 测试集预测值与实测值之间的相关系数为0.967. 当前与机器视觉相关的大蒜自动化产线研究还尚未见报道， 虽然大蒜形态各异， 但从整体上看， 每头大蒜的不同特征属性表现出一定的相关性. 基于这一假设， 本文以机器视觉技术为手段， 构建大蒜的形状特征空间， 采用机器学习方法建立回归预测模型， 实现对待切须大蒜的蒜胡周长预测， 为自动化切须提供技术支持.

1 图像预处理与形状特征采集

为建立大蒜蒜胡尺寸信息的预测模型， 需要对大蒜果实部分进行识别， 建立基于大蒜几何特征的训练集. 本文利用视觉系统从两个角度采集大蒜图片， 如图 1 所示， 通过图像处理技术提取每头大蒜果实区域的12个几何特征： 宽度(X1)、 高度(X2)、 轮廓长度(X3)、 最小外接圆半径(X4)、 最大内接圆半径(X5)、 边界到中心的平均距离(X6)、 最大直径(X7)、 最小外接矩形半长(X8)、 最小外接矩形半宽(X9)、 面积(X10)、 两种不同计算方法的圆度(X11，X12)、 以及在切除蒜须后测得的大蒜蒜胡的周长， 如图 2(d)所示.

图 1 图像采集Fig.1 Image acquisition

欲实现大蒜果实目标的提取， 首先要将整个大蒜区域与背景分割开， 阈值法是一种快速的分割算法， 设图像中某一点像素的灰度值为f(x,y)， 根据式(1)将图像进行二值转换， 变换后的图像用g(x,y)表示.

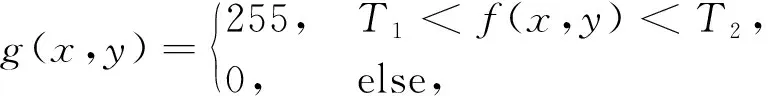
(1)

式中：T1和T2表示阈值， 将背景与目标区域分开， 确定阈值是关键. 本文在环形光源下进行图像采集， 亮度均匀， 且目标区域与背景的对比度较大， 直接采用Otsu法[7-8]进行分割， 得到整个大蒜区域的二值图像， 分割效果如图 2(b) 所示. 完成大蒜与背景的分割后， 还需将大蒜的蒜须分割开. 本文设计了基于形态学的循环分割算法， 过程如图 3 所示， 对图像进行多次分割， 直到得到目标区域. 通过上述处理， 实现果实的目标提取， 分割的目标轮廓效果如图 2(c) 所示.

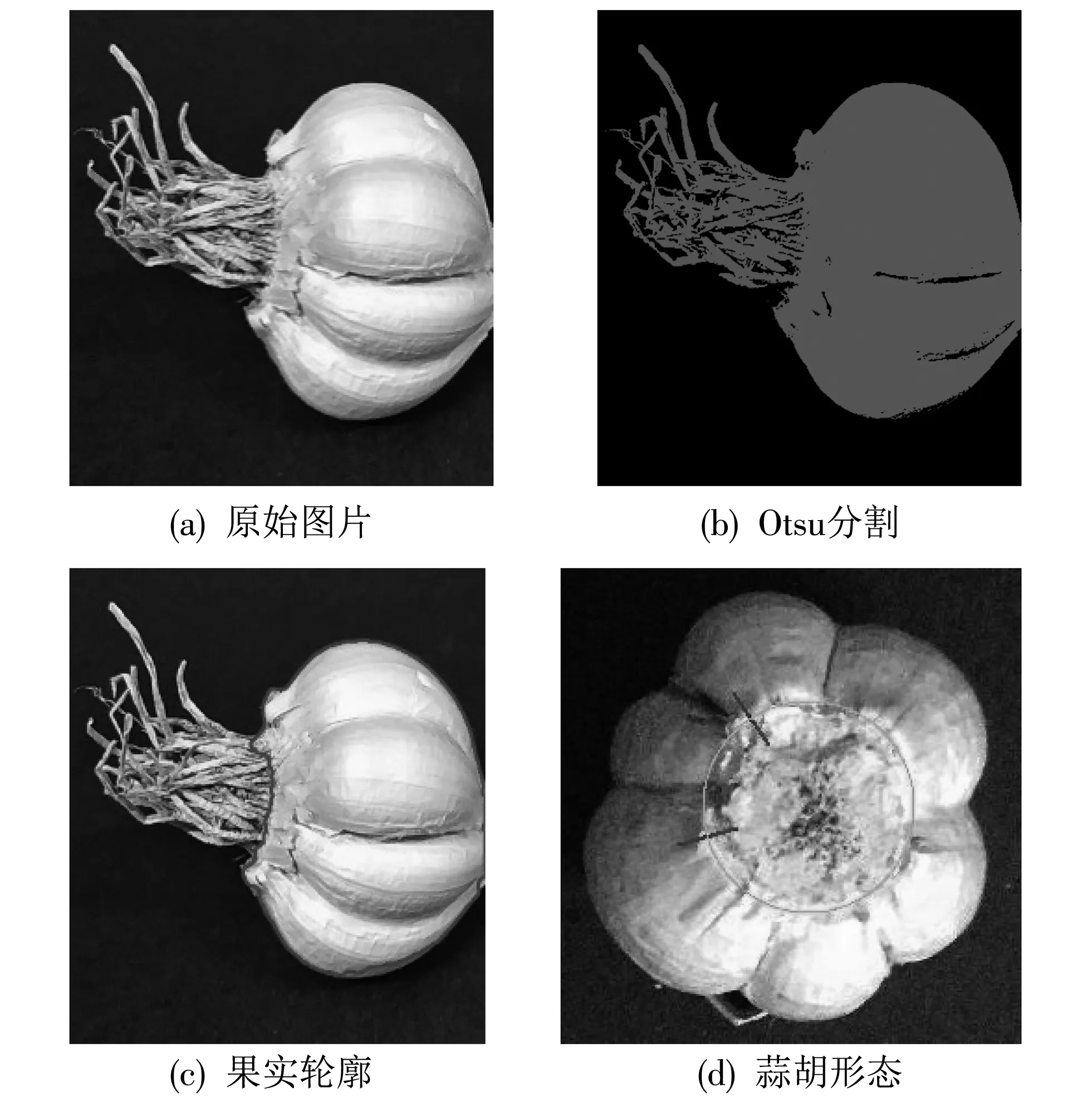
图 2 大蒜图像分割处理实例Fig.2 Garlic image segmentation processing example

本文随机选取200头大蒜做为研究对象， 利用机器视觉技术， 共获得200组数据， 每组数据包含大蒜的12个几何形状特征以及大蒜蒜胡的周长. 随机选取100组数据作为训练集样本建立预测大蒜蒜胡尺寸的预测模型， 另外100组数据作为测试集样本. 计算并统计目标区域的形状特征， 其中大蒜像素面积分布范围为 95 274～355 218 像素， 平均像素为198 292像素， 中位数为200 728像素， 大蒜的圆度分布范围X11为 0.797 9～0.961 3，X12为 0.563 3～0.700 4. 其他数据分布用箱形图绘制， 如图 4 所示， 箱形图能显示出一组数据的最大值、 最小值、 中位数及上下四分位数， 为使箱型图更加直观， 所有轮廓长度X3均缩小 10倍. 不同大蒜样本的某个特征属性的分布情况均表现出一定的差异性， 但从整体上看， 每头大蒜的不同特征属性又表现出一定的相关性. 所以采用大蒜的多个特征属性联合回归预测大蒜蒜胡的尺寸大小.

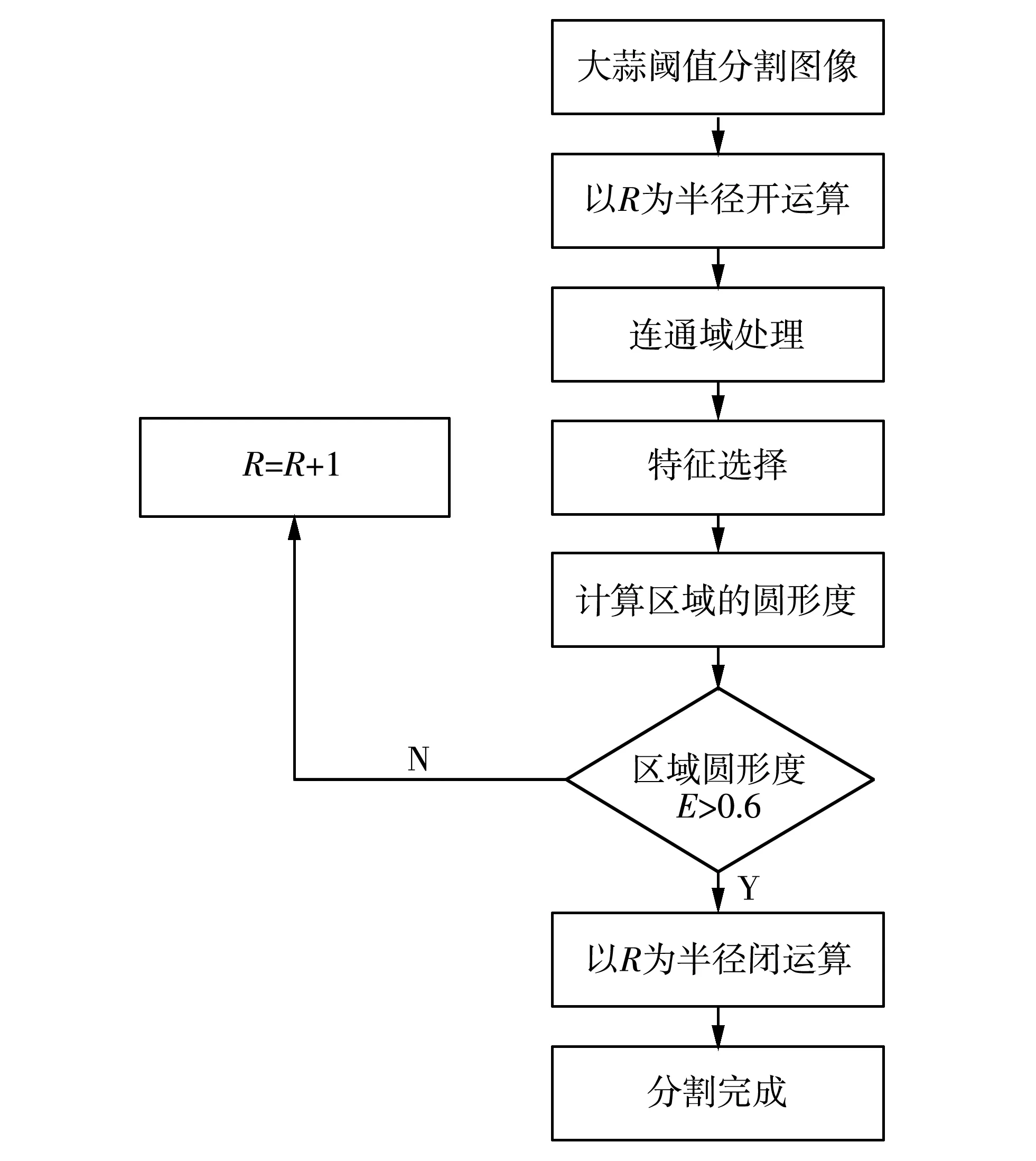
图 3 大蒜蒜须分割流程图Fig.3 Flow chart of garlic beard segmentation

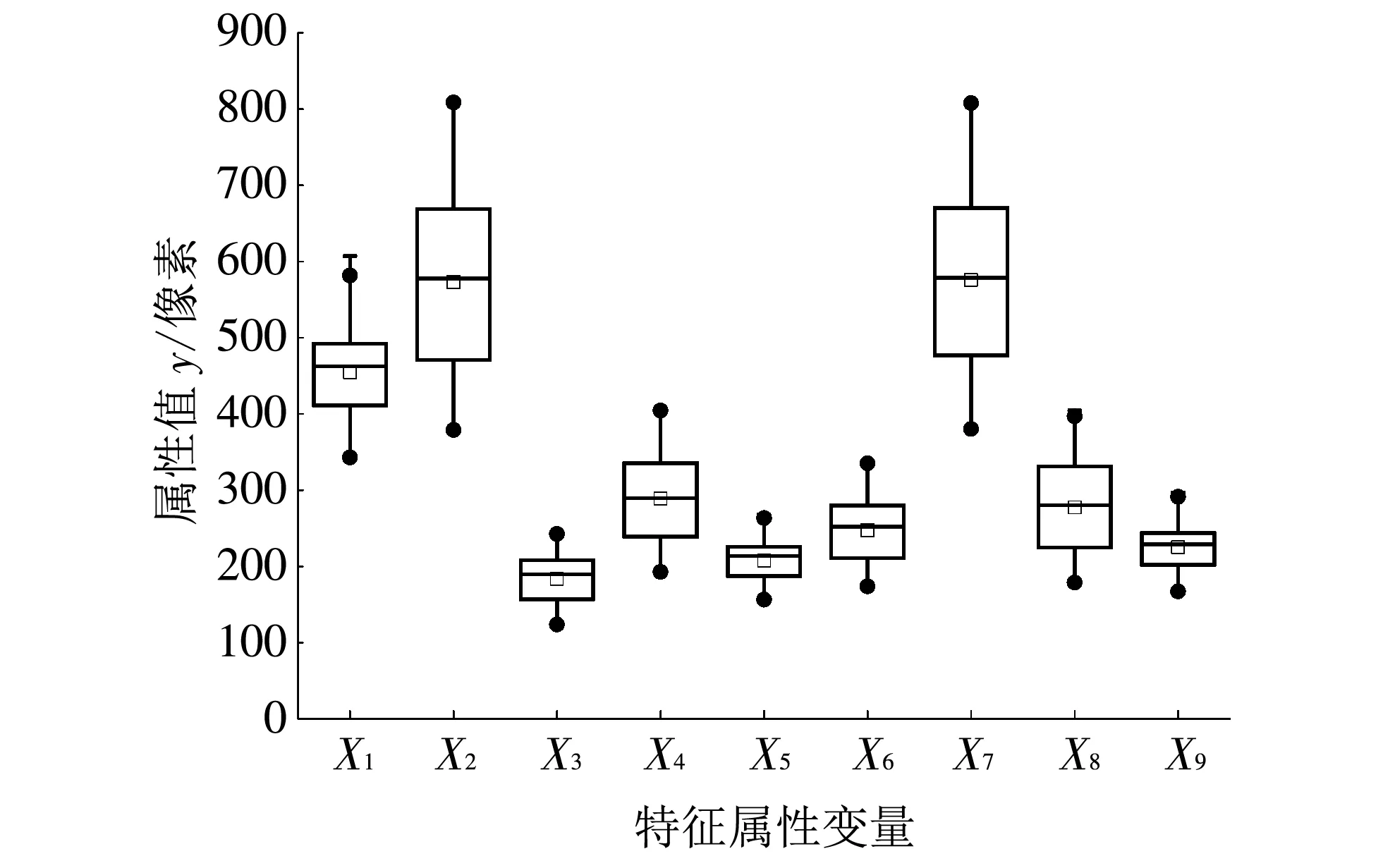
图 4 大蒜特征属性数据分布Fig.4 Garlic characteristic attribute data

2 回归预测模型的建立

本文设计了BP(Back Propagation)神经网络和基于核函数的支持向量回归机(SVR)模型， 对蒜胡周长进行预测.

2.1 基于BP神经网络的预测模型

BP神经网络是一种多层前馈神经网络， 该网络的主要特点是信号前向传递， 误差反向传播， 通过调整网络权值和阈值， 使误差沿梯度方向下降， 从而使BP神经网络预测输出不断逼近期望输出[9-10]. 基本数学描述如下：

假设输入层输入向量为X=(x1,…,xi,…,xn)T， 隐含层输出向量为Y=(y1,…,yj,…,ym)T， 输出层输出向量为O=(o1,…,ok,…,ol)T， 输出层期望输出向量为D=(d1,…,dk,…,dl)T. 当网络输出与期望输出不等时， 存在输出误差ε， 定义如下

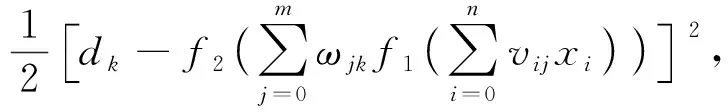
(2)

式中：vij和ωjk为BP神经网络权值；f1表示输入层到隐含层激励函数；f2表示隐含层到输出层激励函数.

工作信号的正向传播和误差信号的反向传播调节各层权值的过程是周而复始的， 每个权值的修正值为

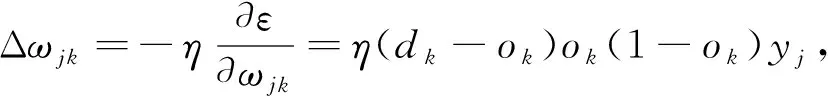
(3)

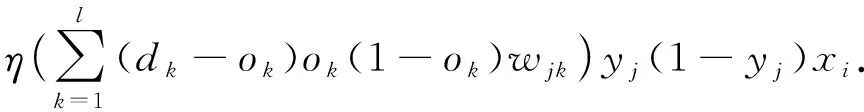
(4)

将大蒜的12个几何特征(X1～X12)作为神经网络的的输入参数， 确定输入层神经元个数为12， 最佳隐含层节点数为[11]

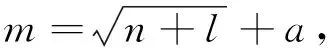
(5)

式中：m为隐含层节点数；n为输入神经元数；l为输出神经元数；a为0～10之间的经验值. 经计算， 本文中隐含层神经元数在4～13之间， 通过网络性能测试确定隐含层节点数为10， 输出层神经元个数为1， 即为大蒜蒜胡的周长. 所以BP神经网络的结构采用12-10-1三层结构.

2.2 SVR回归预测模型

SVR作为支持向量机(SVM)处理拟合回归问题的一类模型， 通过建立训练数据中的待预测向量与支持向量间的非线性关系， 对待预测向量进行预测. SVR的主要思想是建立一个高维的回归曲面， 让数据集内所有样本点到该平面距离最近[12-13]. 已知数据样本是12维向量， 训练集可表示为{(xi,yi),…,(xk,yk)}， 其中xi∈R12为输入变量， 即大蒜果实区域对应的12个几何特征，yi∈R为大蒜蒜胡周长. 此时构建回归超平面

f(x)=ω·x+b,

(6)

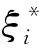
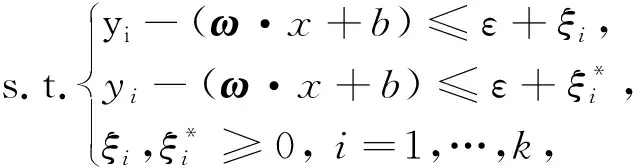
(7)

式中：ε为损失界限， 控制了模型对数据的误差宽度. 对上式的优化求解问题可以引入Lagrange乘子a、a*， 将凸二次优化问题转变为对偶问题

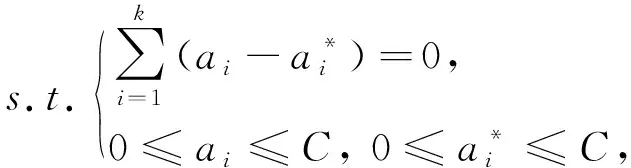
(8)

最终得到的回归函数为

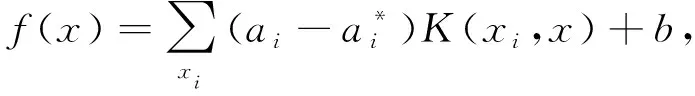
(9)

式中：K(xi,x)表示核函数. 构建一个高性能的支持向量机模型， 关键是选择恰当的核函数及参数. 关于SVM参数的优化选取， 国际上并没有公认统一的最好方法， 采用交叉验证(Cross Validation， CV)的思想可以在某种意义下得到最优的参数[14]， 本文在SVM相关参数的优化过程中使用K-CV方法.

3 结果与分析

3.1 基于BP神经网络的预测结果

本文利用MATLAB神经网络工具箱来完成网络拓扑结构设计、 权值初始化、 网络训练和结果输出. BP神经网络的初始化权值由[-1,1]的随机数产生， 并选用Newff函数初始化网络， 所训练的模型参数设定为： 最大训练次数为1 000， 网络性能目标误差为0.004， 学习率为0.1. 选用train函数训练BP神经网络， 用BP神经网络预测函数sim输出. 将所有样本数据(13×200)在[0,1] 内进行归一化， 并随机排序， 选择其中100组数据作为训练集， 其它作为测试集. 网络学习样本数据输入经过多次迭代， 在训练57次时网络训练误差值达到 0.003 997 5， 逼近设定的最大允许误差0.004， 说明神经网络是收敛的. 预测结果如图 5， 图 6 所示， 预测值与实测值的相对误差绝对值在0.04%～13.08%之间波动， 平均绝对百分比误差为3.59%， 具有很好的一致性.

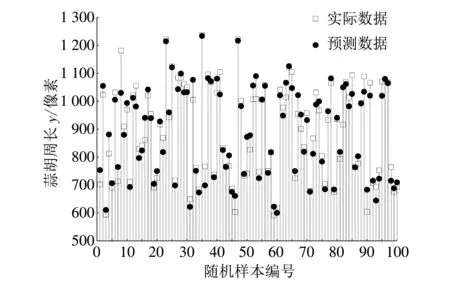
图 5 BP神经网络回归预测与实际数据对比Fig.5 Comparison of BP neural network regression prediction and actual data

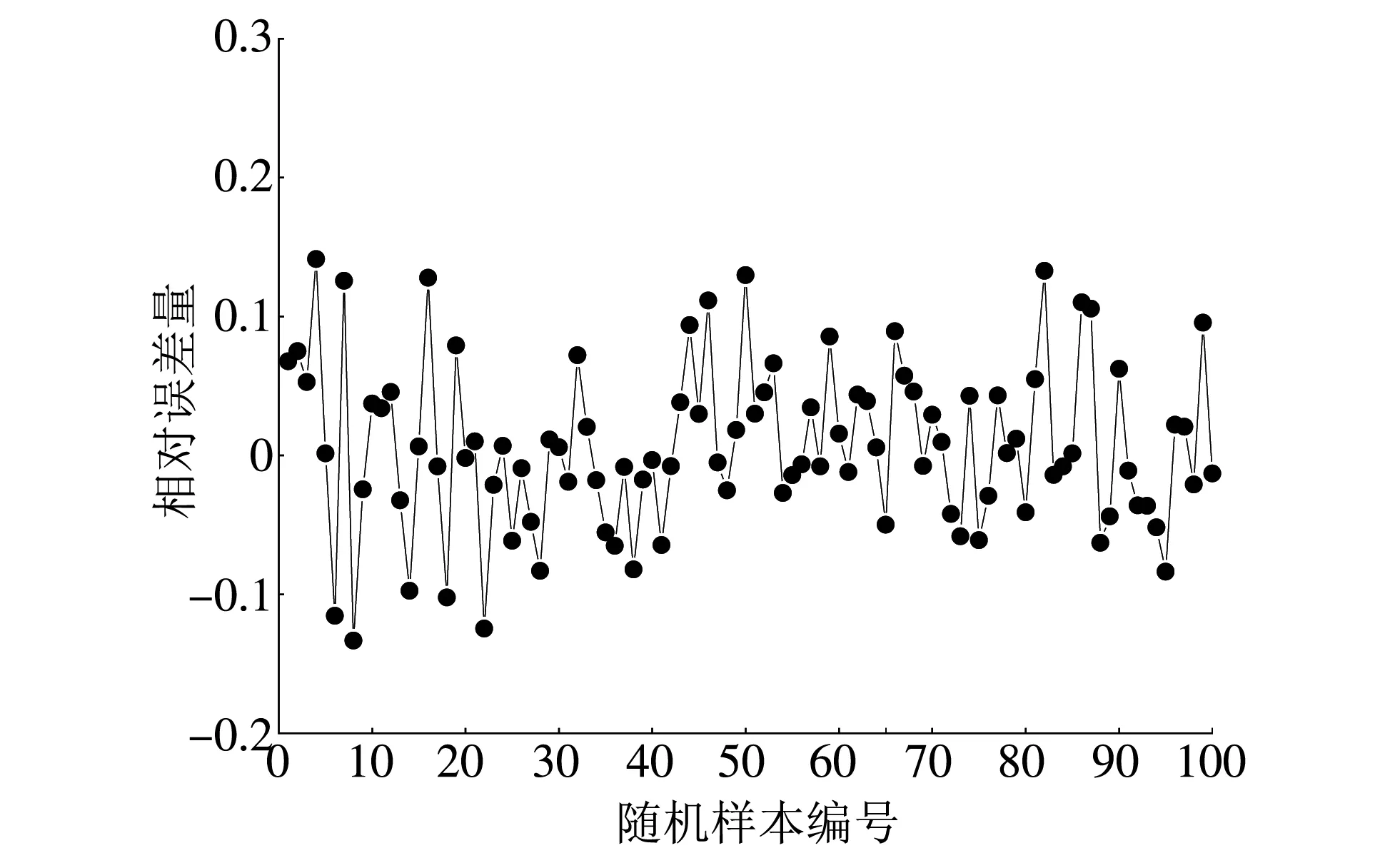
图 6 BP神经网络测试样本相对误差图Fig.6 BP neural network test sample relative error graph

3.2 基于SVR的预测结果

训练样本和测试样本与BP神经网络的训练集和测试集完全相同. 在MATLAB R2014b环境下， 利用支持向量机库libsvm-3.22进行训练和测试. 为得到最优的预测模型， 通过K-CV方法优化惩罚因子C和核函数参数g， 并将其应用到SVR模型中. 采用均方误差(MSE)对不同核函数的SVR预测结果进行分析， MSE值越大， 预测值与实测值的偏差就越大. 不同核函数的SVR预测结果如表 1 所示.

由表 1 可知， 选取线性核函数的预测值与实际值之间的MSE最小， SVR可实现较优的预测效果. 预测结果如图 7、 图 8 所示，预测值与实测值的相对误差绝对值在0.14%～14.14%之间波动， 平均绝对百分比误差为4.62%， 一致性较好.

表 1 不同预测模型结果评价

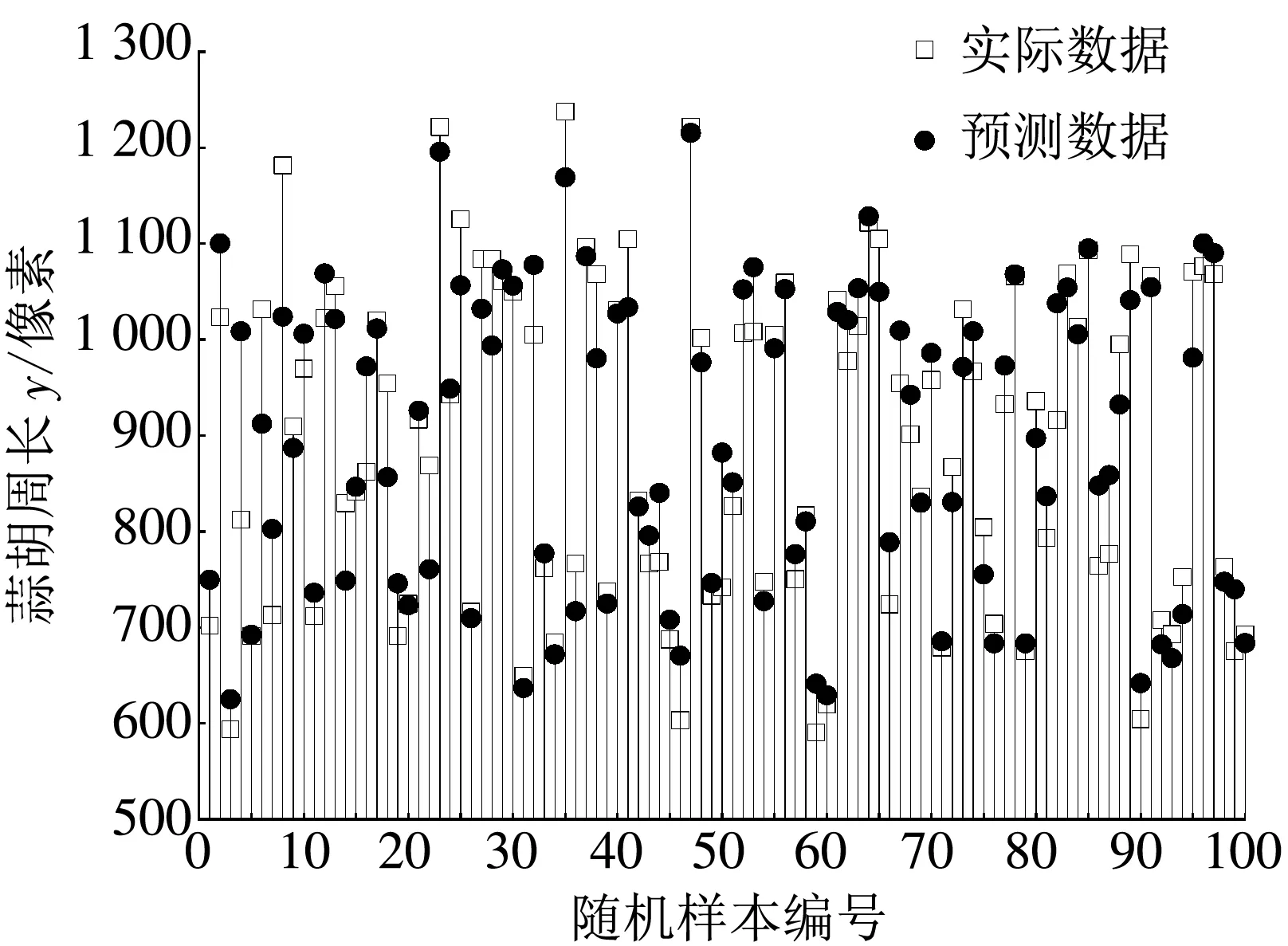
图 7 SVR回归预测与实际数据对比

Fig.7 Comparison of SVR regression prediction and actual data

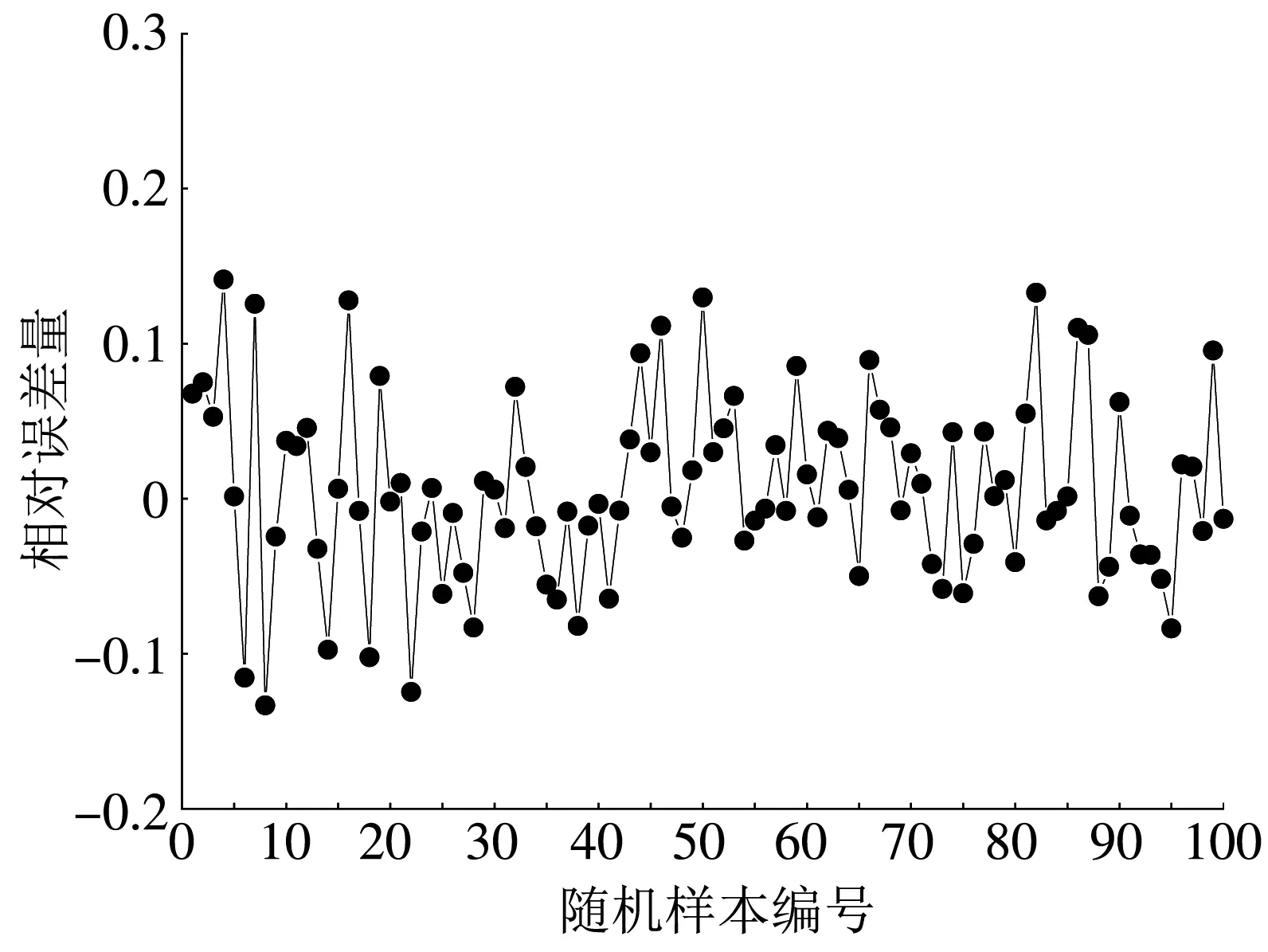
图 8 SVR测试样本相对误差图

Fig.8 SVR test sample relative error graph

3.3 预测结果分析

由图 5～图 8 可知， 依据大蒜的几何特征所建立的两种回归预测模型， 其蒜胡的形态尺寸的预测值与实测值的趋势基本吻合.

图 9， 图 10 分别为BP神经网络模型测试样本的网络输出值y与网络期望输出值x的回归直线， 以及基于线性核函数的SVR的回归直线. 由图 9， 图 10 可知， BP神经网络和SVR的回归直线与直线y=x偏差不大， 其中BP神经网络的回归直线的相关系数R=0.967 03， SVR的回归直线的相关系数R=0.924 88. 由上述结果可看出， 大蒜蒜胡周长的预测值与实际值具有较好的一致性， 以大蒜果实区域几何特征建立的预测模型可实现有效的回归预测.

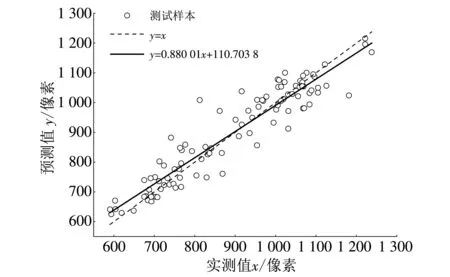
图 9 SVR测试样本输出回归曲线Fig.9 SVR test sample output regression curve

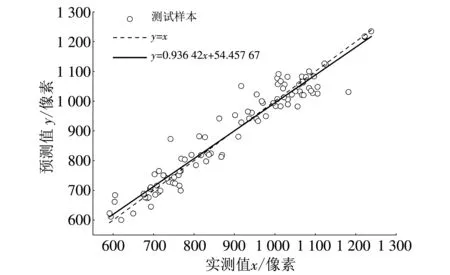
图 10 BP神经网络测试样本输出回归曲线Fig.10 BP neural network test sample output regression curve

4 结 论

本文针对大蒜蒜胡形态尺寸预测问题， 以机器视觉技术手段， 提出了基于几何形状特征的蒜胡尺寸预测方法. 通过提取大蒜果实部分的12个几何形状特征建立的预测模型预测的大蒜蒜胡周长与实际值的趋势基本一致， 表明这些特征作为预测变量的有效性. 机器视觉技术结合机器学习方法用于大蒜蒜胡尺寸的预测， 为大蒜机械化切须提供了一种新方法， 有望彻底解决大蒜除须难题， 成为提高劳动生产率的重要手段， 或将成为精准农业领域的研究热点.