动车组轮装制动盘螺栓安装工艺及其影响研究*
2020-07-13张化谦杨伟君焦标强吕宝佳曹建行
张化谦, 杨伟君, 焦标强, 吕宝佳, 曹建行
(1 中国铁道科学研究院 研究生部, 北京 100081;2 北京纵横机电科技有限公司, 北京 100094)
动车组轮装制动盘由紧固件(螺栓、螺母、螺栓套)连接安装。为保证其连接可靠,需保证安装后螺栓内部的预紧载荷处于规定范围。传统的人工扭矩法通过人工施加一定的扭矩,从而间接保证规定的预紧载荷,但在实际生产中受多种因素的影响,该方法很难保证预紧载荷的准确性与不同螺栓预紧载荷之间的一致性。
动车组长期处于高速度、高振动的运行工况下,轮装制动盘螺栓还要承受制动时的高热量,因此对连接的可靠性要求较高,相关文献也对其运用故障进行了分析[1],认为控制好螺栓紧固效果有助于避免自身及配合件的故障[2],研究方法主要包括试验测试与仿真计算[3]。不同行业的应用表明,为达到较好的紧固效果,应从研究安装工艺入手,既寻找现有工艺中可能引发故障的因素[4],也探究先进的螺栓拧紧技术[5],例如机器扭矩转角法,从而进一步提高连接质量、提高效率。机器扭矩转角法在航空航天、汽车领域已广泛应用,但在轨道交通行业的研究较少[6]。
拟开展使用机器扭矩转角法和人工扭矩法的研究工作,通过螺栓拧紧机控制扭矩、转速、角度等参数,保证螺栓内部预紧载荷的准确性与一致性,并提高效率,降低劳动强度,保证轮装制动盘生产、运用的安全可靠。
1 螺栓受载情况分析
轮装制动盘螺栓所受载荷可分为热载荷与机械载荷两部分,耦合作用主要表现为螺栓受热膨胀后影响其轴向载荷大小,所以分析轮装制动盘螺栓运用过程中的受载情况,应首先分析其受热情况。
轮装制动盘螺栓吸收外部热量的过程是典型的非稳态传热,即系统中各点的温度与位置、时间均有关系,可表示为T=T(x,y,z,t);且存在热传递(Heat Transfer)的3种基本方式,即:热传导(Heat Conduction)、热对流(Heat Convection)、热辐射(Heat Radiation)[7]。传递途径如图1所示。

图1 轮装制动盘装配体热传递示意
根据Fourier定律可知,热传导量ΦCond为:
(1)
正常情况下,螺栓不会直接接触到高温部位,而是通过图 1的红色路径,完成轮装制动盘与螺栓的间接热传导。式(1)中,ACond为受热接触面积,-λ·dt/dx为x方向导热的热流密度,其中λ为导热系数。虽然导热系数λ较大,但是受热接触面积ACond较小,且经过了螺栓套、螺母的衰减,故由热传导引起的螺栓温升较小、影响面积较小、效果较为滞后。
根据Newton冷却公式可知,热对流量ΦConv为:
ΦConv=AConvhΔt
(2)
式(2)中,AConv为受热对流面积,h为热对流系数,Δt为温度差。其中热对流系数h与材料无关,主要取决于流体流动状态、流体物理性质、壁面温度、壁面几何形状等。在较为密闭的螺栓孔腔内部,空气流动性差且比热容低,因此热对流几乎不会引起螺栓温升。
根据Stenfan-Boltzmann定律可知,热辐射量ΦRad为:
ΦRad=εARadσT4
(3)
式(3)中,ε为发射率,ARad为受热辐射面积,σ为黑体辐射常数,T为黑体绝对温度。根据Kirchhoff定律可知,处理工程问题时,通常将分析对象看做漫灰体,即其光谱发射率与波长无关,且其辐射吸收率恒等于同温度下的发射率ε[7]。因此在制动过程中,螺栓总是吸收来自高温处的辐射热。且热辐射的载体为电磁波,受媒介、距离的影响较小,故螺栓受热辐射面积ARad较大、温升较快。热辐射量ΦRad与黑体绝对温度T的四次方成正比,因此在轮装制动盘迅速升温的过程中,螺栓最主要的热量便来源于高温位置的热辐射。
在螺栓内部,热传导方向与温度梯度方向相反,因此受热传导与热辐射的影响,螺栓两端的温升较为明显,内部传热路径为由外圈向内圈、由两端向中部,从而导致螺栓出现轴向热膨胀[8]。
在安装阶段,施加安装扭矩可提高螺栓连接的可靠性、防松能力与疲劳强度,此时产生的初始轴向载荷即为预紧载荷。在制动阶段,相较于螺栓吸收的热量,轮装制动盘吸收的热量较多、速度较快,因此轮装制动盘率先膨胀变形,造成对螺栓的轴向拉伸,使得螺栓在初始预紧载荷的基础上,其轴向载荷增加至最大值,而螺栓受热膨胀滞后,螺栓伸长量会逐渐大于轮装制动盘变形量,使得螺栓轴向载荷较最大值有所降低。在冷却阶段,轮装制动盘与螺栓的热量逐渐散失、热弹性变形逐渐恢复,螺栓轴向载荷随冷却时间的延长而恢复到初始状态。
在运用过程中,轮装制动盘螺栓在初始预紧载荷的基础上承受振动冲击载荷和热载荷,其轴向载荷总是先增大再减小,一旦超过螺栓材料的屈服极限,便会引起塑性屈服失效,载荷过大会产生断裂。在列车反复制动时,可认为螺栓总是承受单向交变载荷的作用,当交变载荷有较多的冲击过载或随机载荷时,工作应力在某些时刻会越过疲劳极限。因此在长期运用过程中,轴向载荷的变化会导致应力幅差别,进而导致疲劳寿命的差别,所以应着重考察螺栓的预紧载荷与螺栓载荷在运用过程中的变化情况。
2 安装试验对比
为准确对比人工扭矩法、机器扭矩转角法两种安装工艺的效果与效率,现针对某型号轮装制动盘设计了对比试验。该型号轮装制动盘由12组紧固件连接,安装时以固定的扭矩与顺序依次拧紧并校核。螺栓只承受静载荷工况时,预紧载荷F0经验公式、对应安装扭矩T经验公式分别为[9]:
F0=(0.6 ~ 0.7)σs·As
(4)
T=K·F0·d
(5)
其中,σs为螺栓的屈服强度;As为螺栓在螺纹处的有效截面面积;K为螺栓连接副中安装扭矩与预紧载荷的关系系数;F0为预紧载荷;d为公称直径。该型号轮装制动盘的螺栓预紧载荷F0控制在50 kN,范围在40~70 kN之间,对应的安装扭矩T控制在160 N·m,范围在130~200 N·m之间(上述数值的确定不在文中研究范围内)。
由式(4)~式(5)可知,螺栓安装效果的评估指标主要为预紧载荷与安装扭矩,安装拧紧时应将螺栓变形控制在弹性段内,因此前者可通过如图 2(a)所示的超声波接收片、图2(b)所示的超声波测距仪,测量螺栓安装前后的弹性变形量,并结合标定结果计算得出。后者则在安装时由人工读取扭矩扳手数值、机器记录实际扭矩数值得出。其中安装扭矩是对安装过程中的最终扭矩进行监控,以确保得到准确的螺栓预紧载荷,因此应重点关注预紧载荷的准确性与一致性。

图2 测试及安装设备
使用两种工艺分别安装2套轮装制动盘,分别记录完整安装一套轮装制动盘的时间、两种安装工艺下各螺栓的预紧载荷与安装扭矩,从而得到两者在安装效率、预紧载荷准确性与一致性方面的差别。安装试验前对螺栓完成拉伸标定、粘贴头部超声波接收片、测量初始长度等工作。两种安装工艺均由两人配合完成,人工扭矩法安装需扭矩扳手及辅助工具若干,机器扭矩转角法安装则仅需借助如图2(c)所示的螺栓拧紧机,便可完成安装、校核、记录等步骤。
经过记录可知,安装一套轮装制动盘,人工扭矩法耗时为25 min,机器扭矩转角法耗时为20 min。考虑到随着工作时间的延长、工人体能的下降,人工扭矩法的安装耗时会有所增加,所以改用新安装工艺能在一定程度上提高生产效率。
人工扭矩法安装的数据记录如表1所示,分析结果可知,有3颗螺栓的预紧载荷接近65 kN,较标准值增大了近30%,5颗螺栓的预紧载荷接近40 kN,较标准值减小了近20%;在相邻两颗螺栓中,1号轮装制动盘的5、6号螺栓预紧载荷差值达到13.7 kN,接近控制范围的50%;所有螺栓的安装扭矩均为160.0 N·m,符合要求。由此说明,人工扭矩法安装时,安装人员通过设置扭矩扳手上限值,及时读取扭矩数值并反馈调整力度,虽然易于得到准确的安装扭矩,但该工艺得到预紧载荷的离散程度较大,存在超出控制范围的风险。

表1 人工扭矩法安装数据记录
机器扭矩转角法安装的数据记录如表2所示,分析结果可知,所有螺栓的预紧载荷在49.3~57.6 kN之间,安装扭矩在150.0~173.4 N·m之间,均符合要求,且距控制的极限值有一定裕度。由此说明,机器扭矩转角法安装时,螺栓拧紧机通过数据监督和报警、适当调整拧紧参数,虽然得到的安装扭矩的离散程度较大,但是预紧载荷得到了较好地控制。

表2 机器扭矩转角法安装数据记录
为更加直观、准确地进行对比分析,将螺栓预紧载荷、安装扭矩分别绘制柱状图,结果如图3、图4所示;对两种安装工艺数据进行方差分析,结果如表3所示。经分析可知,虽然两种安装工艺得到的螺栓预紧载荷平均值都接近于50 kN,但是人工扭矩法安装得到的方差较大,各颗螺栓受力不均。而机器扭矩转角法安装得到的方差仅为人工扭矩法的10.66%,说明使用该工艺得到的预紧载荷一致性较好。

图3 两种安装工艺的螺栓预紧载荷

图4 两种安装工艺的螺栓安装扭矩

表3 安装工艺数据方差分析
因此机器扭矩转角法的安装效果、效率较优,为进一步证明改进安装工艺的可行性,应对产品的运用状态进行分析,验证较大预紧载荷、较小预紧载荷、相邻螺栓间较大预紧载荷差值对产品运用的影响。
3 产品运用状态模拟分析
结合受力分析与安装试验可知,人工扭矩法安装轮装制动盘螺栓容易引起预紧载荷离散度较高、易超出控制范围的问题,且该问题会进一步导致螺栓与轮装制动盘受载情况与运用状态的差别。为准确量化并对比该差别,可借助有限元模拟技术,建立轮装制动盘装配体的热力耦合模型,通过调整模型设置,即可模拟不同安装工艺下的轮装制动盘螺栓预紧状态。
3.1 有限元模型的建立
轮装制动盘与车轮均是60°的中心循环对称结构,因此取实际产品的1/6扇形区域,建立轮装制动盘装配体的热力耦合模型即可。设置相应的热力耦合分析步,与同时具有温度、位移自由度的网格,使模型可计算输出温度、位移与受力。假设模拟工况为时速350 km纯空气紧急制动,所受载荷包括螺栓的预紧载荷、闸片压力、盘面热流密度,并在车轮内圈设置位移约束、扇形切分面设置对称约束、整体设置热传递条件与环境温度约束。通过设置紧固件间的接触或绑定,可表示螺栓的连接作用,进而模拟不同的状态。
如图 5所示,模型中包括1个1/6的车轮、2个1/6的轮装制动盘、1个定位销、2套相邻的紧固件。在上述模型设置的基础上,假设各组模拟中螺栓1的预紧载荷均为标准值50 kN,仅改变螺栓2预紧载荷的施加,即可模拟对比得到不同安装工艺下的螺栓预紧状态。根据安装试验可知,人工扭矩法安装时预紧载荷较大会接近70 kN,预紧载荷较小会接近40 kN,机器扭矩转角法安装时预紧载荷正常为50 kN,具体设置如表 4所示,对模型进行相应修改并提交计算即可。

图5 三维装配模型

表4 各组模拟的预紧载荷设置
3.2 计算模拟结果并分析
为反映螺栓的运用状态,提取各组模拟中2颗螺栓的轴向载荷随制动时间的变化结果,分别取其载荷差值的绝对值,并绘制曲线,结果如图 6所示。分析可知,螺栓安装时造成的初始预紧载荷差值会伴随制动、冷却过程,且载荷差值大小始终与初始差值相近,在制动后会有所降低,说明预紧载荷较小的螺栓,其轴向载荷变化幅度要大于预紧载荷较大的螺栓,即应力幅较大。因此在一定范围内,施加较大的预紧载荷可以降低螺栓的轴向应力幅,提高其疲劳寿命。
但A组中模拟人工扭矩法安装、预紧载荷为70 kN的螺栓,在制动50~70 s之间,其轴向载荷已达到螺栓材料的屈服极限,表现为保持在110 kN左右不变,因此承受较大预紧载荷的螺栓发生屈服或拉断的风险较大。而B组中模拟人工扭矩法安装、预紧载荷为40 kN的螺栓,在完成制动、开始冷却之后,其轴向载荷下降幅度较大、数值较低,因此承受较小预紧载荷的螺栓在长时间受到振动冲击载荷时不利于保持预紧状态。对比A、B、C组可知,相邻螺栓2的预紧载荷变化对螺栓1的轴向载荷影响不大,无论是数值大小还是变化趋势都较为类似,因此相邻螺栓的预紧载荷差值并不是影响螺栓运用状态差别的主要因素。

图6 各组模拟的螺栓轴向载荷
为反映轮装制动盘的运用状态,提取各组模拟中螺栓轴向载荷最大的时刻,即制动70 s左右的轮装制动盘轴向变形云图。由于实际情况中的变形较小,因此将3组结果中轮装制动盘与螺栓的轴向变形量放大50倍,得到结果如图 7所示。从中可知,A组轴向变形云图中显示橙色的面积最小,略大于C组,B组最小,且主要差别在螺栓2附近,说明预紧载荷越大,对轮装制动盘轴向变形的约束越大,但影响范围仅限于螺栓周围。

图7 各组模拟的轴向变形云图
如图8所示,选取外侧轮装制动盘盘面在螺栓孔处的一周节点,计算得出这些节点的轴向变形量随时间的变化关系,并绘制其平均值的变化曲线,以反映螺栓对附近轮装制动盘在安装、制动、冷却过程中的限制作用。对各组模拟的螺栓1、螺栓2分别进行此操作,并各自取轴向变形量最大点绘制曲线,结果如图 9所示。从中可进一步看出,各组中2个螺栓孔附近的平均变形量之差很小,远小于同最大变形的差值,所以改变预紧载荷无法有效限制轮装制动盘的轴向最大变形,进而也无法消除轮装制动盘最大轴向变形处的不均匀磨耗。随着运用时间的延长,轮装制动盘的磨耗量增大,螺栓孔附近变形差别的影响才会逐渐显现,从而引起局部的提前磨耗到限。

图8 选取节点示意
综上所述,轮装制动盘螺栓的不同预紧状态在短期内引发的问题较少,而随着运用时间的延长,轮装制动盘螺栓的不同预紧状态引起的产品运用状态差别越发突出,包括螺栓疲劳寿命的差别、轮装制动盘磨耗到限的差别,不利于产品的统一检修或更换。因此,通过改进安装工艺,提高螺栓预紧载荷的准确性与一致性,能有效避免上述问题的发生。
4 结 论
(1)安装试验表明:机器扭矩转角法能保证螺栓预紧载荷的准确性与一致性,提高安装效率,减少劳动强度,而人工扭矩法得到的预紧载荷离散度较高,存在超出螺栓预紧载荷限值的风险。
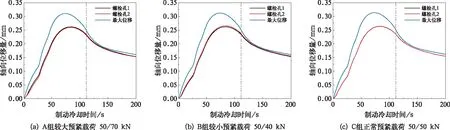
图9 各组模拟的轴向变形量
(2)通过仿真分析可知,提高螺栓预紧载荷的准确性,有助于避免螺栓出现屈服失效、连接松动等潜在故障;提高螺栓预紧载荷的一致性,有助于降低轮装制动盘的磨耗差别,避免产品提前更换。
综上所述,相对人工扭矩法而言,使用机器扭矩转角法安装轮装制动盘螺栓,既能保证良好的安装效果、在一定程度上提高生产效率,又能减少运用中潜在故障的发生。
