基于偏微分方程的GAC水平集图像分割模型

刘 晨，李丙春，王文龙，张宗虎

(喀什大学 计算机科学与技术学院,新疆 喀什 844006)

图像分割[1]是计算机视觉的基础，是图像目标识别、检测和分析等后续处理的第一步，同时也是图像处理中的难题.基于曲线演化理论和水平集方法的几何活动轮廓(geometric active contour，简称GAC)模型[2-5]广泛应用于边缘检、图像分割等领域.在平面图像分割中，其将2维演化曲线表达为高一维的3维连续函数的零水平集，水平集函数定义为演化曲线的符号距离函数，能够较好地处理曲线拓扑结构的变化.但传统的GAC模型在曲线演化迭代过程中需要重新初始化，难以检测出弱边缘轮廓，容易受到噪声的干扰.

GAC模型有基于变分水平集方法的演化方程和以偏微分方程(partial differential equation,简称PDE)驱动的水平集方法的演化方程[6-7]，论文所研究模型属于后者.近年来，出现了较多基于PDE的GAC水平集方法的改进方法.文献[8]提出利用气球力和梯度向量场混合作用改进GAC模型，并且利用半隐式方案加性算子分裂算法对新模型进行加速运算.文献[9]定义一种新的符号压力函数，利用具有图像增强能力的局部区域信息，从而取代GAC模型的边界停止函数，并且使用选择性二进制和高斯滤波水平集方法，取代水平集函数的重新初始化.文献[10]采用基于区域信息的水平集方法，结合GAC模型和Chan-Vese模型提出一种新的活动轮廓模型，提高图像分割的精确性.

传统的GAC水平集方法的图像分割，水平集函数必须周期性地重新初始化使水平集函数保持为一个符号距离函数.论文在原先能量泛函模型中引入一个约束能量，解决了水平集函数在演化过程中需重新初始化的问题.但引入的约束能量是基于变分水平集方法的，直接应用于基于偏微分方程驱动的水平集方法，会出现错误的分割结果，论文在此基础上在引入反应扩散方程，将水平集方程的求解划分为两部分来解决上述问题.传统的GAC模型水平集方程中停止函数直接基于图像梯度信息，论文提出一种新的边缘检测算子，应用到边缘停止函数中，对边缘停止函数给予重新定义.

1 GAC模型

设零水平集函数φ(x,t)，其中x表示平面位置，t为时间参数.定义封闭曲线C(t)，C(t)={x|φ(C(t),t)=0}，因为φ(C(t),t)=0，两边对时间t进行求导得到方程

(1)

初始水平集函数为φ0(x)=φ(x,t=0)， 则GAC模型的水平集函数演化方程为

(2)

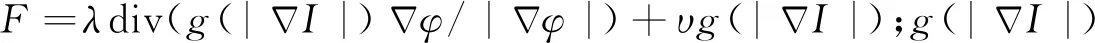
2 论文模型

2.1 无需重新初始化GAC模型

在传统的水平集方法中，为了确保活动轮廓模型的稳定性，防止水平集函数在靠近边缘时候过于平坦或者过于陡峭，初始水平集函数通常将曲线生成符号距离函数，并且在曲线演化迭代过程中必须周期性地重新初始化，使得水平集函数重新变成带符号的距离函数，如果水平集函数发生退化，将导致数值计算的迭代过程趋向不稳定，从而导致错误的分割结果.重新初始化的计算量大，分割速度慢.重新初始化工作[11-12]可以求解PDE方程得

(3)

文献[13]提出一种符号距离惩罚能量函数为

(4)

此能量泛函只与水平集函数φ有关，使得在演化过程水平集分割模型中的约束水平集函数保持为一个符号距离函数，从而曲线在演化过程中不用反复对水平集函数进行重新初始化.其梯度下降流为

(5)

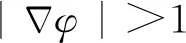
论文将符号距离惩罚能量函数结合GAC模型，得到相应的梯度下降流为

(6)

这种符号距离惩罚能量函数是基于变分水平集方法提出来的，直接应用于基于偏微分方程驱动的水平集方法中，不能有效地正确分割图像.将公式(6)改写成

(7)

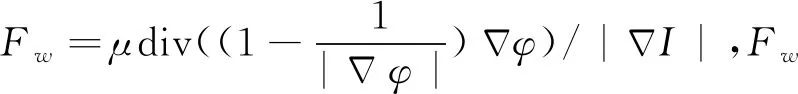
可以用图1中左边所示的图来说明这个问题.图中红色箭头表示水平集方程中的推力函数F，蓝色箭头表示规则化推力函数Fw.在零水平集到达目标边缘时，水平集推力函数F接近于0，当Fw等于0时，水平集曲线停留在目标边缘.而有些时候，当水平集推力函数F等于0、Fw不一定等于0时，零水平集会继续演化，从而导致错误的分割.

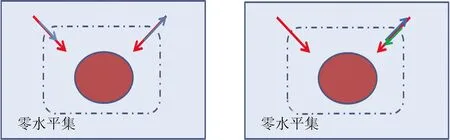
图1 水平集方程演化推力函数

为了解决上述问题，将反应扩散方程理论应用到公式中，得到新的水平集演化方程为

φt=εΔφ+ε-1L(φ),

(8)

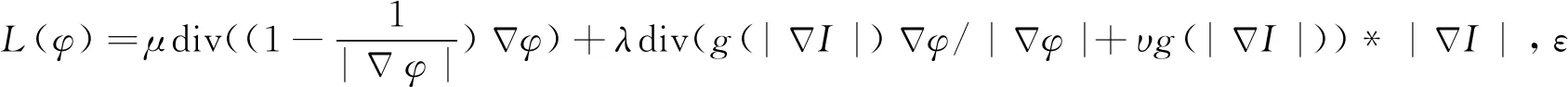
从而将水平集方程的求解划分为扩散部分εΔφ和反应部分ε-1L(φ).根据反应扩散理论研究可知，第一步求解反应方程部分φn+1/2=φn+t1L(φn)，第二步求解扩散方程部分φn+1=φn+1/2+t2φn+1/2.这里忽略ε这一小的正常数，因为在具体的求解过程中可以将参数ε整合进时间参数t1和t2，在具体数值计算中t1和t2都很小，从而得到t1ε-1→t1，t2ε→t2.

可以通过图1右图来说明这个问题.图中红色箭头、蓝色箭头分别表示水平集方程推力函数F和规则化推力函数Fw.论文将反应扩散方程应用到上述无需重新初始化的GAC模型中.新的模型分为两步：第一步求解反应方程部分，但是其惩罚函数是基于变分方程理论提出的，直接应用于偏微分方程并不完全适合；第二步求解扩散方程，修正规则化推力Fw与推力函数F的方向不一致问题，如图中绿色箭头所示.从而新的水平集演化方程为

(9)

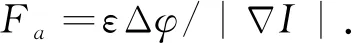
2.2 新的边缘停止函数

GAC水平集模型其边缘停止函数是基于图像梯度信息的，难以分割图像不同区域间模糊的弱边缘和灰度渐进图像目标，并且易受到噪声的影响，抗噪声能力弱.根据文献[14]可知，二阶导数能够有效地区别边缘和渐变区域.定义

并且提出了一种差分曲率的边缘检测算子，表示为D=||uηη|-|uξξ||，其中|*|表示绝对值运算.经过试验，提出一种新的边缘检测算子，应用到边缘停止函数g中.参考uηη和uξξ定义

(10)

省略原先定义形式的归一化操作，定义

(11)

从而提出一种新的边缘检测算子为

(12)

从图2(a1)～(a3)可以看出，在无噪声情况下，3种算子都能有效地检测出渐变图像的边缘，相较于梯度算子和差分算子，论文定义的算子能很好地检测出边缘所在，不受图像其他区域信号影响.如图2(b1)～(b3)所示，在图像受到较为轻微的噪声影响下，论文定义算子几乎不受噪声影响，和无噪声情况下的边缘检测效果一致，而梯度算子和差分算子只有在人工目视情况下可见，受到较为严重的噪声影响.在图像受到较为严重噪声影响下各种边缘加测算子比较如图2(c1)～(c3)所示.论文定义算子依然可以检测出图像边缘，而此时的梯度算子和差分算子在人工目视情况下图像边缘都已不可见.通过上述实验，可知论文提出的边缘检测算子，能有效地检测出图像的边缘，特别是在图像受到噪声的影响下，相较于传统的边缘检测算子具有更好的鲁棒性.论文将提出的边缘检测算子应用到水平集模型中的停止函数，重新定义边缘停止函数，表示为

(13)

图2 无噪图像和噪声图像及边缘检测比较

3 实验结果

通过实验验证论文所提出模型的有效性.论文对比方法有:在原先基于偏微分方程驱动的GAC模型中直接加上基于变分水平集模型的惩罚能量,得到方法1;文献[15]所提出的方法2.在第一个试验中还将添加重新初始化的方法.论文模型参数选取为μ=0.01，υ=0.5，λ=0.8，t1=0.1，t2=0.001.方法1中的参数与论文模型中的参数选取一致,方法2中的参数取其默认参数，可参考文献[15].

实验1针对含有较多复杂边缘的多目标图像进行试验，如图3(a)所示.图3(a)中的红色方框表示初始水平集函数的零水平集,图3 (b)～(e)分别对应重新初始化方法、方法1,2和论文方法的分割结果.从分割结果来看，重新初始化方法分割结果错误，并且耗时.在后面的实验比较中，将不再参与方法的比较.方法1最终的零水平集位置离图像真正边缘还有一定距离，并且在两处边缘中间位置产生了额外的假边缘，如图3(c)所示，说明方法1的分割效果不理想.方法2和论文提出的模型都可以较好地得到分割结果.

图3 原始图像及不同方法下的分割比较

实验2针对弱边缘图像及其受到噪声影响的情况.图4(1)为无噪声图像，图4(2)是添加低噪声水平(噪声标准差为8的高斯噪声)的噪声图像，图4(3)是添加高噪声水平(噪声标准差为16的高斯噪声)的噪声图像.图4(a)～(c)是对无噪声图像图4(1)的分割比较.从图中可以看出：方法1出现了错误的零水平集，也就是错误的边缘，如图4(a)所示；方法2能较好地得到分割结果，但是在弱边缘处分割结果有点瑕疵，如图4(b)右边细胞上方弱边缘处；而论文方法能得到比较好的分割结果，如图4(c)所示；在低噪声和高噪声影响下，方法1都出现了错误的分割结果，如图4(a)，(d)，(g)所示；方法2随着噪声水平的增加，分割结果错误率越来越大，不能有效地分割弱边缘目标，如图4(b)，(e)，(h)所示；而论文方法，不仅在无噪声情况下正确得到弱边缘目标的分割结果，在低噪声和高噪声水平的影响下，也能得到较为正确的分割结果，几乎不受噪声的影响，如图4(c)，(f)，(i)所示.

图4 原始图像、噪声图像及不同方法下的分割结果

论文采用Jaccard相似系数(Jaccard coefficient,简称JC)和骰子相似系数(dice similarity coefficient,简称DSC)[16]对分割结果进行评价，分别定义为

(14)

其中：N(R)表示区域R内像素点的个数;R1,R2分别表示基准目标区域和分割得到的目标区域;JC，DSC的取值范围为[0,1]，取值越大说明该分割方法的分割结果越精确.

实验3是针对不同模型下图3(a)、图4(1)～(3)无噪声和不同强度高斯噪声污染图像的分割精度做定量分析，结果如表1,2所示.从JC和DSC两个量化指标结果可以看出，在无噪声环境下，论文模型分割结果高于重新初始化方法、方法1，2.在不同强度高斯噪声环境下，论文模型和无噪声环境下分割结果数据大致相同，而方法1，2随着噪声水平的增加分割精度随之下降.从量化指标的数据结果分析可以得出论文模型的有效性和适应性.

表1 图3(a)不同模型实验结果的JC与DSC比较

表2 图4(a)，(b)，(c)不同模型实验结果的JC与DSC比较

4 结束语

论文针对基于偏微分方程驱动的GAC模型，提出一种新的水平集图像分割方法.引入一个约束能量，解决了水平集函数在演化过程中需重新初始化的问题.但引入的约束能量是基于变分水平集方法的，直接应用于基于偏微分方程驱动的水平集方法，会出现错误的分割结果.论文在此基础上引入反应扩散方程，将水平集方程的求解划分为两部分，解决了此问题.并且提出一种新的边缘检测算子，重新定义边缘停止函数.实验结果表明，论文提出方法对弱边缘及其受噪声影响图像分割更具鲁棒性，得到较好的分割结果.