有界线性算子L在g-Besselian框架的应用

黄喜娇,肖祥春

(1.安阳学院 数理学院，河南 安阳 455000；2.厦门理工学院 应用数学学院，福建 厦门 361024)

1952年,Duffin等[1]在研究非调和 Fourier级数时提出了Hilbert空间中的框架概念，并对框架的性质做了初步研究.目前，框架理论已被广泛应用于信号处理[2]、数据量化[3]、图像处理[4]等领域.2006年，Sun[5]提出了g-框架的概念，并对g-框架的性质进行了研究，得到许多重要结论.随后，g-框架、无冗g-框架、g-Riesz框架、g-框架序列、g-Besselian框架等逐步被许多学者研究，并且取得了重要的研究成果[5-12].

论文在文献[10]的基础上，运用有界线性算子L的不同性质进一步刻画了g-Besselian框架，且根据文中的结果可以证明其他文献中的定理.

设U和V是两个复Hilbert空间，其内积为〈·， ·〉，范数为‖·‖，{Vj}j∈J是V的闭子空间序列，其中J是整数集Z的子集，L(U,Vj)表示从U到Vj的所有有界线性算子的集合，L(U)表示从U到U的有界线性算子的全体.线性空间l2({Vj}j∈J)定义如下

其内积为

则l2({Vj}j∈J)为一个复Hilbert空间.

1 定义与引理

定义1[5]设Λj∈L(U,Vj),j∈J，则称序列{Λj}j∈J为U关于{Vj}j∈J的g-框架，如果存在正数A,B>0，使得

满足上述不等式的A,B分别称为g-框架的下界和上界.如果只有右边的不等式成立，则称序列{Λj}j∈J为U关于{Vj}j∈J的g-Bessel序列.

引理1[13]设{Λj}j∈J∈L(U,Vj)，且对任意j∈J,dimVj<+∞，{ejk}k∈Kj是Vj的标准正交基，则下列两个叙述等价：

(1){Λj}j∈J为U关于{Vj}j∈J的g-Besselian框架.

(2){Λj}j∈J为U关于{Vj}j∈J的g-框架，且dimkerQ<+∞，其中线性算子

引理2[14]设U，V为Hilbert空间，有界线性算子T:U→V具有闭值域T(U)，则存在唯一的有界线性算子T+:V→U，满足

NT+=T(U)⊥，T+(V)=NT⊥，TT+f=f，∀f∈T(U).

引理3[15]设Λj∈L(U,Vj),j∈J, 则序列{Λj}j∈J为U关于{Vj}j∈J的g-Bessel序列且界为B,当且仅当可定义线性算子Q：l2({Vj}j∈J)→U为

引理4[15]设Λj∈L(U,Vj),j∈J,则序列{Λj}j∈J为U关于{Vj}j∈J的g-框架当且仅当可定义线性算子Q：l2({Vj}j∈J)→U为

且Q为有界满的，框架界为‖Q+‖-2和‖Q‖2，这里Q+为Q的伪逆算子.

引理5[16]设X,Y为Banach空间，T:X→Y，U:Y→X均为有界线性算子，若T和U满足TU=I并且dimkerT<+∞，其中I是Y中的恒等算子，则

X=kerT⊕U(Y)，

dimkerT=dimkerU*.

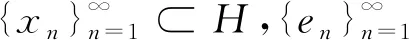
引理7[9]设序列{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架，框架界为A,B,且{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-Bessel序列，若线性算子L[9]是满的，则{Γj:j∈J}是U关于{Vj:j∈J}的g-框架.

2 主要结果及证明

文献[10]中通过举例说明，当{Λj}j∈J∈L(U,Vj)为U关于{Vj}j∈J的g-Besselian框架，且{Γj}j∈J是U关于{Vj}j∈J的g-Bessel序列时，线性算子L是满的，则不能推出{Γj}j∈J是U关于{Vj}j∈J的g-Besselian框架.但是，如果L是可逆的有界线性算子，则上述结论成立，即得定理1.

定理1设{Λj}j∈J∈L(U,Vj)，且对任意的j∈J，dimVj<+∞.假设序列{Λj}j∈J是U关于{Vj}j∈J的g-Besselian框架，序列{Γj}j∈J是U关于{Vj}j∈J的g-Bessel序列，若线性算子L是可逆的，则{Γj}j∈J是U关于{Vj}j∈J的g-Besselian框架.

证明由于序列{Λj}j∈J是U关于{Vj}j∈J的g-Besselian框架，根据g-Besselian框架的定义知{Λj}j∈J为U关于{Vj}j∈J的g-框架，根据引理4可定义有界线性算子为

且由引理1知dimKerP<+∞，再根据引理7知{Γj}j∈J为U关于{Vj}j∈J的g-框架.

要证{Γj}j∈J是U关于{Vj}j∈J的g-Besselian框架，根据引理1，下面只需证明dimKerQ<+∞.

设任意的f∈U，经计算知P的共轭线性算子

P*:U→l2({Vj}j∈J)，P*f={Λjf}j∈J∈l2({Vj}j∈J)，

又序列{Γj}j∈J是U关于{Vj}j∈J的g-Bessel序列，根据引理3可定义有界线性算子

所以，对任意f∈U，有

即L=QP*.因为L是可逆的有界线性算子，所以由L=QP*，可得I=L-1QP*.由于

(L-1QP*)*=P(L-1Q)*，

所以

P(L-1Q)*=I*=I.

根据引理5，得dimkerP=dimker(L-1Q)，因为L是可逆的有界线性算子，所以dimkerQ=dimkerP<+∞.又因为{Γj}j∈J是U关于{Vj}j∈J的g框架，再根据引理1知{Γj}j∈J是U关于{Vj}j∈J的g-Besselian框架.

注1令Λjf=〈f,fj〉，Vj=C,j∈J，由文献[11]中的定理2.1和定理2.2可知，{Λj}j∈J为U关于{Vj}j∈J的g-Besselian框架当且仅当{fj}j∈J为U的Besselian框架，再根据引理6可得文献[15]中的定理4.3.

推论设序列{Λj∈L(U,Vj):j∈J}为U关于{Vj:j∈J}的g-Besselian框架，{Γj∈L(U,Vj):j∈J}为U关于{Vj:j∈J}的g-Bessel序列，若{Γj:j∈J}为{Λj:j∈J}的交错对偶框架，则L=I.

证明由交错对偶框架的定义及文献[8]中有界线性算子L的定义，知L=I.

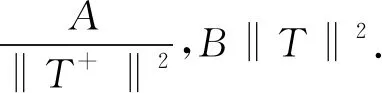
证明设序列{Λj}j∈J是U关于{Vj}j∈J的g-Besselian框架，由g-Besselian框架的定义知，{Λj}j∈J是U关于{Vj}j∈J的g-框架且dimkerP<+∞，其中有界线性算子

P：l2({Vj}j∈J)→U，

且

根据g-框架的定义可以得到，对任意f∈U,有

故有

即框架上界为B‖T‖2.

另一方面，因为T∈L(U)是一个满的算子，根据引理2，则对任意f∈U,有TT+f=f，所以，有

‖T+‖-1‖f‖≤‖Tf‖，

所以，{ΛjT}j∈J是U关于{Vj}j∈J的g-框架，根据引理4可定义有界线性算子为

因为

所以,有

Q({gj}j∈J)=T*P({gj}j∈J)，

即Q=T*P.

若a∈kerQ，则Q(a)=0，即T*P(a)=0，因为T是满的，所以T*是单的，故P(a)=0，即a∈kerP，kerQ⊂kerP.

若a∈kerP，则P(a)=0，T*P(a)=0，即Q(a)=0，a∈kerQ，所以kerP⊂kerQ，kerQ=kerP.

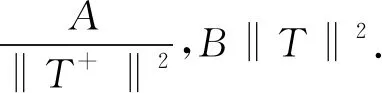
注2令Λjf=〈f,fj〉，Vj=C,j∈J.由文献[11]中的定理2.1和定理2.2可知，{Λj}j∈J为U关于{Vj}j∈J的g-Besselian框架当且仅当{fj}j∈J为U的Besselian框架.由引理6知，在Hilbert空间中，{fj}j∈J为U的Besselian框架与{fj}j∈J为U的拟Riesz基二者是等价的，所以由{Λj}j∈J为U关于{Vj}j∈J的g-Besselian，可以推出{fj}j∈J为U的拟Riesz基.故由定理1可以得到文献[16]中的定理1.