应用G′/(G′+G+A)展开法求解两类非线性薛定谔方程

洪宝剑,陈 威,卢殿臣

(1.南京工程学院 数理部，江苏 南京 211167； 2.南京工程学院 电力工程学院，江苏 南京 211167； 3.江苏大学 理学院，江苏 镇江 212013)

随着现代科技的迅猛发展，人们认识到自然界中的许多问题本质上是非线性的，如光学、电磁学、流体力学和生物科学等.因此，非线性问题的求解对于揭示许多非线性现象具有重要意义[1].同时,人们发现分数阶偏微分方程在描述一些物理性质时比整数阶方程更有效,如描述材料的电性质、电磁波的边界效应、分形动力学和神经细胞中离子的反常过程等.作为描述非线性波重要偏微分方程——非线性薛定谔方程,被广泛应用于几乎所有的物理分支和其他自然科学领域.然而，其精确解的构造却是一项十分困难的工作.迄今为止，国内外学者提出了许多求解非线性微分方程的方法，如齐次平衡法[2]、达布变换法[3-4]、分步傅里叶变换法[5]、贝克隆变换法[6]、Jacobi椭圆函数法[7-8]等.在这些求精确解的方法中，文献[9]首先提出了G′/G-展开法，文献[10-13]扩展了这种展开法的应用，文献[14]将G′/G-展开法应用于分数阶系统，文献[15]首先提出了G′/(G′+G)-展开法.论文主要用广义G′/(G′+G+A)-展开法讨论广义非线性薛定谔方程[16-19]和一类时空分数(1+1)维耦合非线性薛定谔方程[20-21]，获得了其新形式的精确解，这些解为研究某些非线性现象提供了新的依据.

1 推广的G′/(G′+G+A) 展开法基本思想

对于给定的非线性偏微分方程

F(u,ut,ux,uxx,uxt,utt,…)=0，

(1)

其中：u=u(x,t) 是未知函数;F是一个由u=u(x,t) 和其各阶偏导数构成的多项式，包括高阶偏导数项和非线性项.

G′/(G′+G+A)展开法求解步骤如下：

步骤1对方程(1)作行波变换

u(x,t)=u(ξ)，

(2)

其中：ξ=p(x-ct)，p,c为待定常数.

将式(2)代入式(1)，得到只含变量ξ的常微分方程

H(u,u′,u″,u‴,…)=0，

(3)

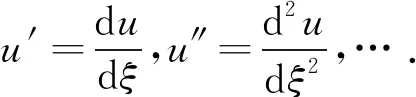
步骤2假设式(3)的解可表示为

(4)

且G=G(ξ) 满足二阶偏微分方程

G″+BG′+CG+AC=0，

(5)

其中：ai,A,B,C为待定常数；正整数m通过齐次平衡法确定.

步骤3将式(4)代入方程(3)，得到关于G′/(G′+G+A)的多项式.令G′/(G′+G+A)的不同次幂系数为零，得到关于a-m,a-m+1,…,a0,…,am-1,am,p,c和A,B,C的代数方程组.利用Mathematica软件求解代数方程组，得到的解再代入式(2)，则可以获得非线性偏微分方程的下列精确解:

情形1Δ=B2-4C>0,有

(6)

则P(ξ)=G′/(G′+G+A)，且

(7)

情形2Δ=B2-4C<0,有

(8)

则

(9)

满足

P′(ξ)=(B-C-1)P(ξ)2+(2C-B)P(ξ)-A,

(10)

其中:C1,C2为任意非零常数.

2 应用G′/(G′+G+A) 展开法求解广义薛定谔方程

考虑下列广义非线性薛定谔方程[16-19]

(11)

其中:α0,γ1,γ2,γ3为任意常数.该方程主要描述光孤子在单模光纤中的传输.

作行波变换

(12)

将式(12)代入方程(11)后，设虚部和实部分别为0，有

(13.1)

p2(1-3γ1κ)φ″+(ω-κ2+γ1κ3)φ+(α0-γ2κ)φ3=0.

(13.2)

将方程(13.1)积分一次，并令积分常数为0，有

(14)

根据相容条件，方程(14)系数应满足

(15)

则方程(14)可以简化为

αφ″-ηφ+βφ3=0,

(16)

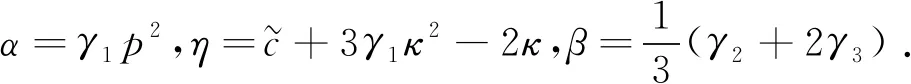
应用齐次平衡法可得m=1，有

(17)

将(17)式代入方程(16)，得到关于G′/(G′+G+A)的多项式，合并相同幂次，并令系数为0，得到

(18)

运用Mathematica软件求解(15),(18)，得

解组1

(19)

解组2

(20)

分别将式(12)，(19)，(20)代入(17)，得到方程(11)的两组解：

情形1当B2-4C>0时，得到方程(11)的孤立波解为

当C1=C2,B=2,u1,2退化为奇异波

情形2当B2-4C<0时，得到方程(11)的三角函数周期波解为

u7,8(x,t)=

当C1=C2,B=2时，u1,2(x,t)退化为文献[15]解组中的式(19)，u1,2(x,t)～u7,8(x,t)是新解.方程(11) 部分解的结构在图1～4中给出.

图2 |u1|在参数t=0时的平面图

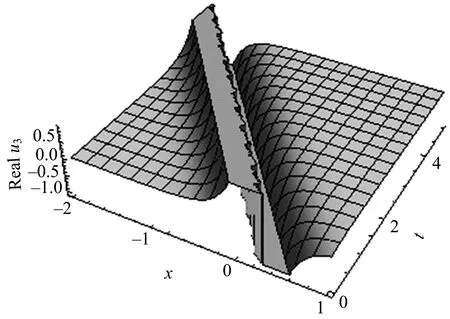
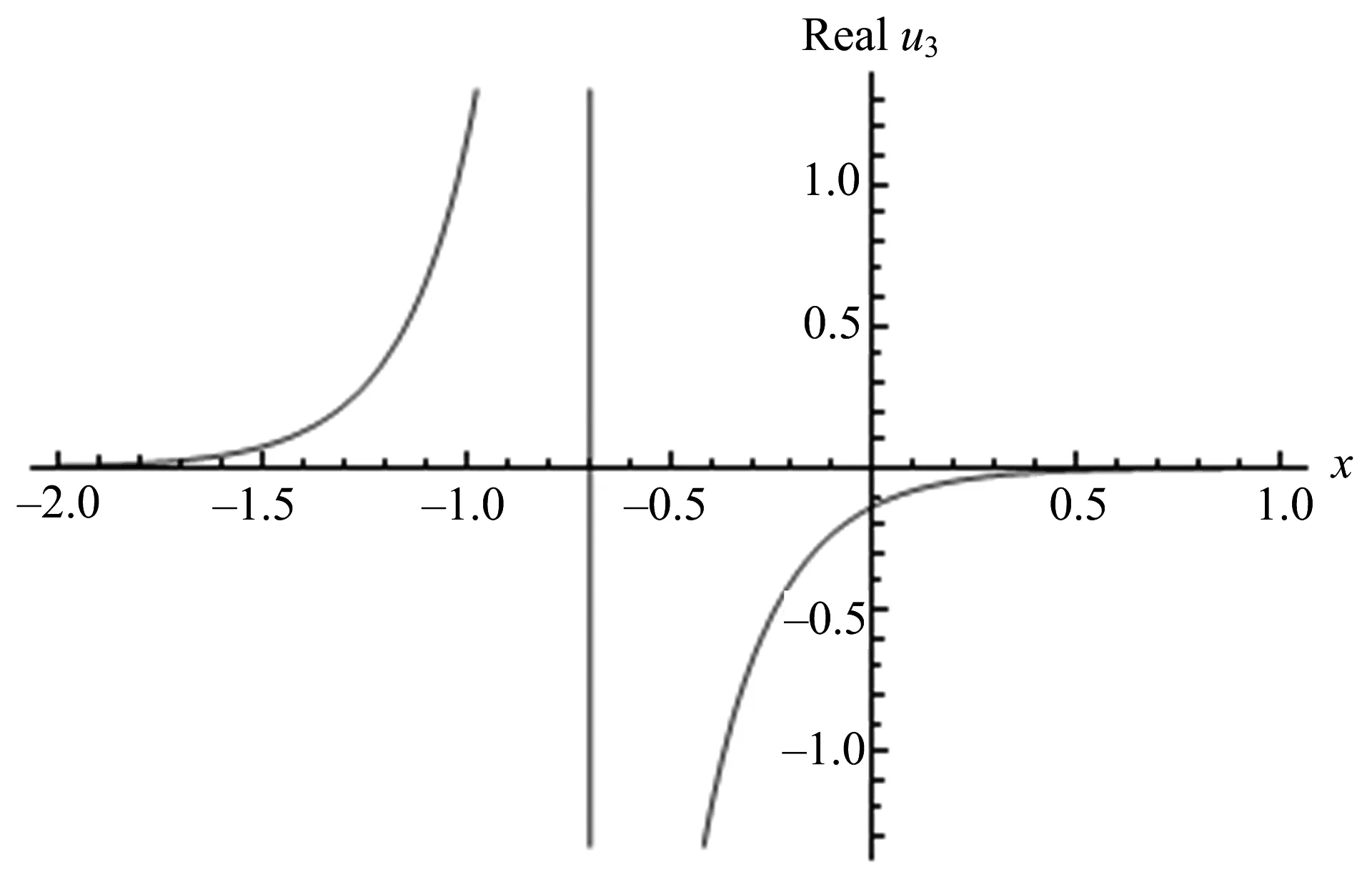
图4u3实部在t=0时的平面图

3 分数阶耦合薛定谔方程的精确解

3.1 分数阶导数的定义和性质

众所周知，分数阶导数定义有很多，较为经典的是Riemann-Liouvile(R-L)型分数阶导数和 Caputo分数阶导数的定义[22]，部分情况下，Riemann-Liouville分数阶导数可以转换为Caputo分数阶导数[22-23].

论文主要采用 Caputo导数定义[22-24]

(21)

其中:α>0,n∈N,x>0.

Caputo导数具有下列性质

(22)

3.2 用G′/(G′+G+A) 展开法求分数阶耦合薛定谔方程

研究一类时空分数阶(1+1)维耦合薛定谔方程[20-21]

(23)

分数阶复变换[25-26]为

(24)

将式(24)代入(23)后，令实部和虚部都等于0，有

(25)

由方程(25)得到

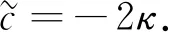
(26)

根据齐次平衡法，假设方程组(25)的解为

(27)

将式(27)代入方程组(25)中，得到关于G′/(G′+G+A)的多项式，合并相同幂次，并令系数为0，得到两个方程组

(28)

(29)

借助Mathematica软件求解 (28),(29)，有

解组1

(30)

解组2

b1=-a1,b-1=-a-1,ω=-κ2-8(C-1)μ2,B=2C.

(31)

将 (26)，(30)，(31)代入方程(27),可以得到方程(23) 的下列解:

情形1当B2-4C>0, 方程(23) 有下列孤立波解

q1,2(x,t)=

u1,2(x,t)=-q1,2(x,t).

u3,4(x,t)=-q3,4(x,t).

特别地，当C1=C2,B=2时,u3,4退化为奇异波解

u′1,2(x,t)=-q′1,2(x,t).

情形2当B2-4C<0, 方程(23) 有下列三角函数解

u5,6(x,t)=-q5,6(x,t).

u7,8(x,t)=-q7,8(x,t).

方程(23) 部分解的结构如图5～8所示.

图6q5虚部在t=0时的平面图

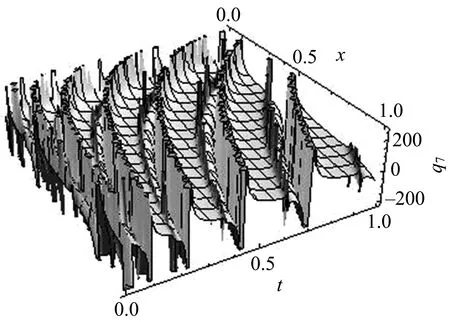
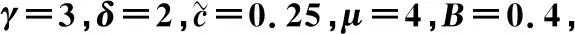
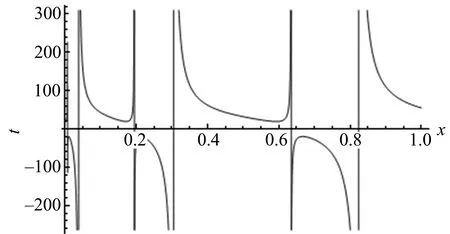
图8q7虚部在t=0时的平面图

4 结束语

应用推广的G′/(G′+G+A) 展开法分别讨论广义非线性薛定谔方程和一类时空分数阶(1+1)维耦合薛定谔方程组，获得了方程(组)的孤立波解、奇异波解和三角函数解，这些解对解释某些物理现象提供了一些帮助，但方程(组)的其他类形式的解依然有待进一步研究.