星地认知网络能效谱效联合博弈功率控制算法
2020-07-13陈威龙郭子桢
陈威龙, 梁 俊, 肖 楠, 刘 明, 丁 然, 郭子桢
(1.空军工程大学信息与导航学院, 西安,710077;2.94303部队, 山东淮坊,261000)
卫星网络因能覆盖到复杂山区、戈壁等边远区域,近年来逐渐受到各国的重视并大力发展。但是由于5G技术的快速发展,地面5G频段与卫星频段冲突日益严重。基于认知无线电的认知抗干扰技术近年来受到许多关注,而功率控制是认知无线电资源分配的重要手段之一[1],功率控制算法通过调整各个认知用户的发射功率,对于合理配置网络资源,提高网络容量有着重要的作用。博弈论的提出对于解决各用户之间的功率竞争问题带来了新思路,近年来已被广泛运用到认知网络的功率控制研究中[2]。
文献[3]设计的PRA算法避免了主用户的干扰同时又考虑了网络能效,但网络容量较小。文献[4]提出了一种鲁棒功率控制方法以此来减小能量损耗,却忽略了各节点的能量剩余情况。文献[5]提出的功率控制算法使功率资源更加公平地分配给各个用户,但是没有考虑能量问题。文献[6]提出的算法综合考虑吞吐量与用户之间公平性,但对于不同用户的需求差异性没有体现。文献[7]提出的NETMA算法提前为各用户分配信道,然后再进行功率控制,但是需要预先规划,不能动态调整。
综上所述,目前的功率控制算法有的没有考虑能效;有的仅仅单一考虑了能效,却没有考虑不同用户的需求;有的预先分配信道,却不能根据主用户的变化而动态调整,并且已有的大部分研究建立的模型采用的是自由空间传播模型,均未将卫星用户采用的是定向天线考虑进去,并且都是将卫星用户统一为一类用户,而没有考虑到不同用户的特点。在星地网络中,移动用户以能效为优先目标而对于地球站用户是以提高通信质量为首要目标。因此,本文联合用户能效与谱效,考虑不同用户的需求,以满足不同需求的最大化为目标,建立能效与谱效联合博弈功率控制模型,提出了一种星地认知网络能效谱效联合博弈算法,最后给出并分析了仿真结果。
1 系统模型
1.1 基本模型
本文考虑的是星地网络多用户共存的功率控制问题,星地认知网络模型如图1所示,N个卫星用户为认知用户,其中包括移动用户和地面站用户,M个地面用户为授权用户。地面用户与基站通信,卫星用户即认知用户采用定向天线与卫星进行通信,卫星传输链路采用Rayleigh模型,卫星用户采用underlay模式选择某地面用户的频段与其共享[11],即本模型共有可用信道M个。
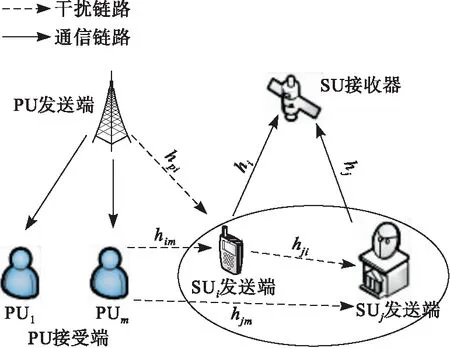
图1 星地认知网络模型
考虑上行链路,卫星用户与地面用户共享统一信道时会相互干扰。第i个卫星用户到卫星的通信链路增益为hi,第m个地面用户到卫星用户的链路增益为hpi,第j个卫星用户到第i个卫星用户的路径增益hji则卫星用户的信干比为[12]:
(1)

(2)
用户i的归一化容量C表示为:
C=
(3)
由式(3)可知,增大卫星用户i的功率或选择干扰小的信道均能提高信道容量。因此,卫星用户的功率大小和信道选择会对通信质量产生影响。
1.2 传输能耗模型
用户之间进行数据传输时,会带来能量的消耗。参考文献[9],本文假设卫星用户向卫星发送lbit数据,且距离为d。则卫星用户i的能耗为:
Ec(i)=Eell+εαld4
(4)
式中:εαld4为信号传输的能耗;Eel为信号发射电路发送1 bit数据的能耗。卫星传输链路采用Rayleigh模型,则可得[13]:
(5)
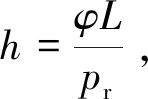
(6)
随着发射功率的增大,卫星用户进行数据传输的能耗随之增大,而对于采用蓄电池供电的认知移动用户应进行有效的信道选择与功率控制,选择干扰较少的信道并尽可能减少发射功率而减少损耗。
1.3 能效因子与谱效因子
在卫星认知网络中,每个用户选择的最优功率和最佳信道应该由能量效率与频谱效率来体现,下面给出能效因子与频谱因子的定义。
现有的大部分研究中将能效定义为速率与速率之比,而对于频谱效率,目前国内外功率控制研究中关于谱效的定义较少,由于本文在能耗模型中以传输数据量为界定,定义了能效因子,并且考虑每个用户选择信道的容量,给出谱效因子的定义,最后将两者相加作为联合因子的定义。
定义1能效因子e为网络中传输单位数据所需的功率大小,即:
(7)
从式(7)可以看出,e越大,单位功耗内传输的数据量越大,同样的功耗传输了更多的数据,能量效率也就越高。
定义2谱效因子f为网络中用户的信道容量的和,即:
(8)
对于式(8),f越大信道容量越大,通信性能越好,频谱效率也就越高。
定义3联合因子c为能效因子e与谱效因子f之和,即:
c=e+f
(9)
通过式(9)可以看出,能效和谱效因子越大,联合因子越大,若其中一个减小,则联合因子也会减小。因此,可以通过式(7)和(8)来比较各算法能效与谱效的优化性能,并且可以通过式(9)来体现算法的联合优化性能。
1.4 博弈论模型
每个认知用户在博弈中都是自私的,他们都想使自身收益最大。本文的博弈模型可表示为G={I,pk,u},其中[14]:
1)博弈参与者I:表示为I={1,2,…,n},n为参与博弈用户即卫星用户个数。

3)效益:博弈者一般用函数来表示自身收益。在本文的模型中,每个卫星用户为了提高自身通信性能都会自私地增大发射功率,但是随着链路功率增大会带来能效的下降并对其共享频谱的用户产生干扰从而带来谱效因子的下降。因此,为联合考虑能效与谱效,并考虑对地面用户的干扰,设计效益函数如式(10)所示:
ui=
(10)
式中:γ*为信干比门限且是常数;α为量级因子,λ为惩罚因子。函数各部分解释如下:
log(1+Υi)是卫星用户的容量,网络容量对通信效率有直接的影响,这部分表明选择干扰小的信道和增大功率均能提高其容量。当用户i的容量越大,效益函数也越大;
log(2+Υ*)引入了信干比门限,如果链路信干比λ<λ*,效益函数值为负,无法进行数据传输。因此为了正常传输,必须使卫星用户的信干比高于最低信干比门限。
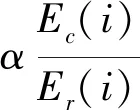

综上,如果卫星用户i的功率不断增加,容量和能耗都会增加而使得能效因子减小;同时,选取干扰小的信道会增加效益函数值而使得谱效因子增加。因此,卫星用户i要选取合适的功率和信道来使自身效益值以及联合因子达到最大。
1.5 最优解的存在性证明
证明:首先通过效益函数ui对pi一阶求导得:
(11)
再将式(11)对pi求二阶导数得:
(12)
式(12)显然小于0,可知博弈模型中每个卫星用户均存在最优解。令∂ui/∂pi=0,求得用户i的最优解为:
(13)
2)在本文模型中,由于网络中地面用户数是整数且可知的,任意卫星用户i总能选择一条收益最佳的信道,因此网络中每个用户均存在干扰最小的可接入信道。
综上所述,网络中每个用户均存在最优功率和最佳信道。
2 能效与谱效联合博弈算法
基于上述模型,本文采用最佳响应策略,提出了一种能效与谱效联合博弈算法COAES[17]。
定义4最佳响应策略:第k轮博弈中每一个卫星用户可根据上一轮博弈中其他卫星用户的策略结果来评估并在策略空间中选择使自己利益最大的策略。
即:
(14)
COAES算法流程图见图2。

图2 COAES算法流程图
根据上述算法,任意用户i在当前轮会根据其他用户的选择更新自身参数,不断地使自身效益值达到最大值,即ui(k)≥ui(k-1)⟹∑j∈N,j≠iuj(k)≥∑j∈N,j≠iuj(k-1)恒成立。同时,所有用户的效益值在相互博弈过程中都是单调非减的,当所有效益值不变达到稳定状态时一定是每个用户最优的选择即纳什均衡状态[18]。
3 仿真与分析
3.1 参数设置
本文通过MATLAB软件对COAES算法进行仿真与分析,设星地认知网络中有5个地面用户,卫星用户数固定时数量为5,其中3个地面站用户,2个移动用户。仿真参数设置见表1。

表1 仿真参数设置
本节选取PRA算法[3]和NETMA算法[7]作为COAES算法的对比算法,通过不同条件设置来比较3种算法。
图3为3种算法在卫星用户数为2~7时的平均发射功率。

图3 卫星用户平均功率随卫星用户数的变化
从图3可知,NETMA算法高于其他2个算法。这是因为NETMA算法是先为用户随机分配信道再进行功率控制,PRA算法是选择对主用户干扰最小的信道,而COAES算法在对卫星用户进行功率控制的同时对接入的信道进行博弈选择。因此,COAES算法的平均功率比其他2种算法小进而产生能量消耗也比较小。
图4为3种算法随着卫星用户数提升时每个卫星用户的平均干扰。从图4可以看出,COAES算法与PRA算法相较于NETMA算法受到的干扰明显降低,因为这2种算法在用户博弈过程中进行功率博弈的同时对信道的选择也进行了博弈,各用户都选择到了自身受干扰最小的信道,并且COAES算法的各卫星用户的通信质量相较于其他2种算法是最好的,即频谱效率最高。

图4 卫星用户平均干扰随卫星用户数的变化
图5为3种算法在用户剩余能量为100%~10%时的平均发射功率。从图5可以看出,随着网络剩余能量的减少,COAES算法和PRA算法均能通过功率控制与信道选择对网络中的发射功率进行调整,而NETMA算法没有考虑能量问题因此功率不变,因为COAES算法和PRA算法均考虑了用户传输的能量消耗,对发射功率进行动态调整,网络的能耗进一步降低。

图5 卫星用户平均功率随网络剩余能量的变化
图6为卫星用户数为5时,随着移动用户剩余能量的减少,移动用户与地面站用户的平均发射功率发生的变化。从图6可以看出,地面站用户无需考虑能量问题,因此功率基本不变,而移动用户随着自身能量的减少发射功率逐渐降低,但由于在卫星用户间的博弈过程中选择干扰较小的信道,因此可以满足最低信噪比的通信需求。
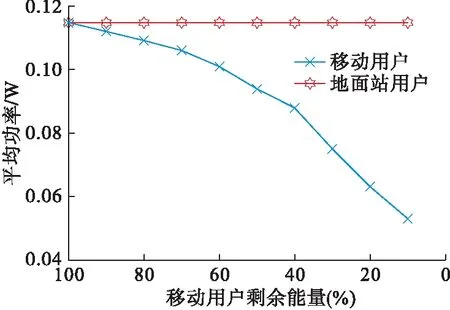
图6 星地网络不同用户随剩余能量的变化
为了更好地比较3种算法,假设某一地面用户的功率逐渐增加,通过前文定义的能效因子、谱效因子以及联合因子来比较3种算法。
从图7可以看出,频谱效率COAES算法与NETMA算法接近,PRA算法最差。因为NETMA算法不考虑能量效率,为了提高通信质量,在不超过地面用户正常通信的规定阈值下会不断地提高卫星用户发射功率,使谱效因子不下降;而PRA算法会由于防止对主用户的干扰而降低发射功率,造成谱效因子的降低。从图8可以看出,能量效率COAES算法最高,PRA算法次之,NETMA算法最低。因为NETMA算法没有考虑能量问题,PRA算法随着地面用户功率提高为了考虑能效而使某些卫星用户信干比达不到通信阈值,无法进行通信造成能效因子的降低。从图9可以看出,联合因子COAES算法相比PRA与NETMA算法分别提升了35%和50%,并且随着功率增加联合优化因子基本保持不变。这是因为PRA算法只考虑了能量效率,NETMA算法只考虑了频谱效率而COAES算法则联合考虑了能量效率与频谱效率,达到了能效与谱效的联合最优。
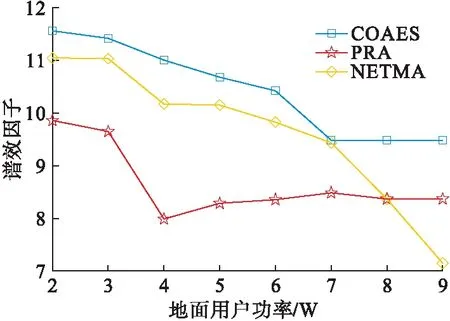
图7 3种算法谱效因子随某一地面用户功率的变化

图8 3种算法能效因子随某一地面用户功率的变化
4 结语
本文研究了卫星认知网络分享地面网络资源功率控制问题,针对卫星网络用户之间的不同,考虑了地面站的用户通信可靠性与移动用户能效性的要求,建立了卫星网络多用户能效谱效联合博弈模型。随后,基于该模型设计了一种能效谱效联合优化算法COAES,并能使每个用户达到最优状态即纳什均衡状态。最后,将COAES算法与PRA算法和NETMA算法进行性能比较。仿真结果表明,COAES算法能够使得卫星认知用户受到干扰降低,并能满足移动用户的能效需求,对能效与谱效联合优化,从而达到网络效率的最大化。
