认知传感器网络中基于新型感知帧结构的吞吐量优化
2020-07-13张宏伟达新宇薛凤凤高维廷
胡 航, 张宏伟, 达新宇, 薛凤凤, 高维廷, 倪 磊, 潘 钰
(1.空军工程大学信息与导航学院,西安,710077;2.空军工程大学研究生院,西安,710051;3.阳光学院人工智能学院,福州,350015)
物联网时代,无线传感器网络(Wireless Sensor Network,WSN)为其数据采集和事件监控提供了一种潜在的解决方案。随着无线设备和业务的爆炸式增长,工作于ISM(Industrial,Science,Medical)频段的WSN将会受到严重且不可控制的干扰[1]。由于可利用的频谱拥挤且有限,因此将认知无线电技术应用于WSN,认知传感器网络(Cognitive Sensor Network, CSN)有望解决频谱短缺引起的干扰问题,并为数据采集提供高谱效的解决方案[2-3]。
认知传感器网络可以协助实现有效的战场态势感知,满足作战力量“知己知彼”的要求。认知无线电是智能的无线通信系统,能够通过学习来感知周围的环境,并依据环境的改变调整自身的系统参数,以实现动态频谱接入[4]。高效、有效的频谱感知是保障主用户和次级用户服务质量(Quality of Service, QoS)的关键[5-6]。为了减小阴影和衰落效应的影响,研究者们提出了多传感器协作频谱感知方案[7-8]。文献[9]中的作者在保证检测概率的前提下优化感知时间、检测门限和符号序列长度使得能量效率最大。文献[10]考虑绿色供能认知传感器网络,通过优化CSN的感知参数和参与协作的传感器节点数量,使得CSN的平均吞吐量最大。
在传统的协作频谱感知帧结构中,认知节点在感知时隙须中断数据传输[11]。因此,传输时延可能会很长,对于时延敏感的应用其QoS不能得到保障。为了实现持续的频谱感知,可以将主用户频带分为几个子频带,不同的子频带有不同的检测任务[12]。本文提出的新型感知帧结构,将主用户带宽分为2个部分,一部分用来频谱感知和感知结果报告,当主用户不存在时另一部分用来为认知节点传输数据。通过这种方法,认知节点的感知时隙不需要中断数据传输,其QoS可以得到保障。
本文研究基于新型感知帧结构的CSN吞吐量优化问题,如果感知带宽越大,感知性能将更好,认知节点将有更多的传输机会,但随着数据传输带宽的减小CSN的吞吐量也将受到影响。为此,需要研究最佳的带宽分配以提升CSN的吞吐量。分析吞吐量关于感知带宽的单峰特性,通过快速高效的算法得到最优的感知带宽值。实际工作中考虑认知节点的QoS需求,需研究时延QoS约束条件下的CSN的吞吐量优化。分析认知节点传输时延特性,设定时延约束门限,在保障认知节点时延QoS的条件下联合优化感知带宽和汇聚节点判决门限以最大化CSN的吞吐量,提出高效的迭代算法解决了相应的优化问题。
1 系统模型与问题描述
在认知传感器网络中有K个认知节点和一个汇聚节点,假定认知节点知道主用户的传输带宽B。与文献[13]中的协作频谱感知帧结构不同,本文提出新型感知帧结构,如图1所示。主用户的带宽B分为2个部分,分别为Bs和Bt(Bs+Bt=B),其中Bs用来频谱感知和感知结果报告,若检测结果为主用户不存在,认知节点将利用Bt传输数据。如果感知结果为主用户存在,认知节点不传输数据。假定一帧时间为τ,单个节点的报告时间为tr。

图1 新型感知帧结构
在本地感知阶段,认知节点使用能量检测技术判断主用户的状态。根据文献[14],可得到单个认知节点的虚警概率pf和检测概率pd分别为:
(1)
(2)
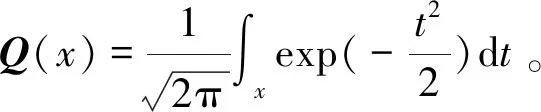
(3)
汇聚节点接收到来自认知节点的感知信息后使用“n-out-of-K”准则进行最终判决,因此协作感知最终的虚警概率Qf和检测概率Qd为[15]:
(4)
(5)

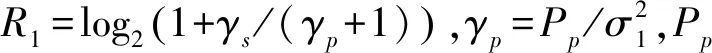
(6)
(7)

(8)
(9)
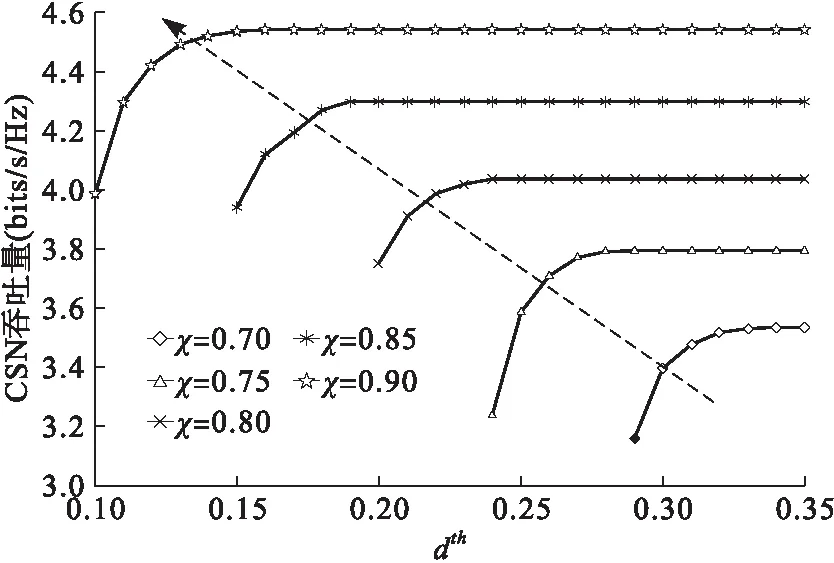
0 (10) 1≤n≤K (11) (12) 其中: (13) (14) T对Bs的一阶偏导数为: (15) 其中: (16) K(pf)n-1(1-pf)K-n(B-Bs)· (17) (18) f(Bs)= (19) 如果函数f(Bs)和g(Bs)在Bs∈(0,B)范围内只相交一次,那么∂T/∂Bs=0的根就是唯一的。下面研究f(Bs)和g(Bs)的性质,求函数f(Bs)关于Bs的一阶导数,可以得到: (20) 其中: (21) (22) (23) 由于u1>0,u2>0,u3>0,所以df(Bs)/dBs>0,f(Bs)是Bs的单调递增函数。下面求g(Bs)关于Bs的一阶导数,能够得到: (24) 依据式(18)和(20),有: (25) (26) 式中:u1、u2、u3和θ在第2节中已给出相关定义。明显可以得到: (27) (28) 由于∂T/∂Bs=0的根存在,所以函数f(Bs)和g(Bs)必定相交。2种可能的情形如下: 1)情形1:f(Bs)和g(Bs)在Bs∈(0,κ]上有交点,由于在区间Bs∈(0,κ]上f(Bs)的增长速度比g(Bs)快,且在Bs∈(κ,B)区间上f(Bs)>g(Bs),所以f(Bs)和g(Bs)有唯一的交点,如图2(a)所示。 2)情形2:f(Bs)和g(Bs)在Bs∈(0,κ]上没有交点,那么他们在Bs∈(κ,B)上必有交点,由于在区间Bs∈(κ,B)上f(Bs)是Bs的单调增函数,g(Bs)是Bs的单调减函数,所以f(Bs)和g(Bs)有唯一的交点,如图2(b)所示。 图2 f(Bs)和g(Bs)的曲线示意图 综上分析,方程∂T/∂Bs=0有唯一的根。因此,在区间Bs∈(0,B)上T是Bs的单峰函数,可使用Bisection算法求得最优的Bs值。对于条件(11),由于n是整数,很难求得最优的n值的解析表达式,但从1搜索到K也并不复杂,所以最优的n值可通过搜索得到。 实际中会考虑认知节点的QoS需求,本小节研究时延QoS约束下的CSN的吞吐量优化。针对图1所示的帧结构,当发生虚警时,认知节点不传输数据,此时传输时延为χQfτ;当成功检测到主用户存在时,认知节点也不传输数据,此时传输时延为(1-χ)Qdτ。因此,归一化的传输时延为: (29) 为了保障认知节点的时延QoS,假定d≤dth,其中dth是时延约束门限。此时,优化问题变为在条件(9)、(10)、(11)和d≤dth条件下最大化吞吐量T。传输时延d对Bs的一阶偏导数为: (30) 图3 不同时延约束情况下CSN的吞吐量 提出时延QoS约束下的吞吐量优化算法如下: 3)比较不同的n值得到的吞吐量Tn,确定最优的Bs值和n值。 为了评估所提算法性能,本节给出了相应的仿真结果。仿真参数设置如下:帧长为τ=20 ms;参与协作的认知节点数量为K=9;主用户的传输带宽为B=2.5×104Hz;次级链路信噪比为γs=20 dB;认知节点接收到主用户信号的信噪比为γ=-10 dB,除非另有声明;主用户不存在的概率为χ=0.8,除非另有声明。 图4 不同目标检测概率不同感知带 图5 不同汇聚节点门限下CSN吞吐量 在不同的χ值下CSN吞吐量随传输时延约束门限的变化曲线如图6所示,该仿真中感知带宽Bs和汇聚节点门限n已联合优化。从该图中也能够观察到:当dth增大到一定值时(dth>d*),CSN的吞吐量达到峰值并保持不变。χ取值越大,CSN吞吐量越高,这是由于认知节点有更多的频谱接入机会可以再利用。不同的χ值将对应不同的d*值,当χ变大时,d*有所减小。 图6 不同χ值下CSN吞吐量和时延约束门限的关系 本文针对认知传感器网络研究了新型协作感知帧结构,构建了吞吐量优化问题,通过对感知带宽的优化分配以最大化CSN的吞吐量。分析了认知节点传输时延约束对吞吐量的影响,联合优化感知带宽和汇聚节点判决门限,在满足时延QoS需求的前提下提升了CSN的吞吐量。提出高效的迭代算法得到了优化问题的解,并在不同情况下仿真分析了所提方案的吞吐量性能。仿真结果表明:所提联合优化方法能够较大程度地提升CSN的吞吐量,改变时延QoS约束条件需要不同的最优感知带宽。

2 CSN吞吐量优化
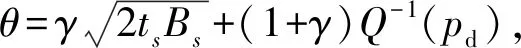
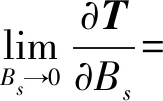








3 时延QoS约束下的吞吐量优化




4 仿真分析




5 结语
