面向智能博弈游戏的卷积神经网络估值方法

唐 杰 许华虎 谈广云

1(上海大学计算机工程与科学学院 上海 200444)2(杭州浮云科技网络有限公司 浙江 杭州 310000)

0 引 言

人工智能研究界中，机器博弈是一个广受关注的领域。机器博弈具有一组有限的定义良好的规则，研究它们可以方便地测试新的方法，从而准确地衡量新方法的好坏程度。测试是通过比较许多与基于其他方法的程序博弈或与人类选手博弈的结果来完成的，这意味着机器博弈拥有一个定义良好的用于测量其发展进程的度量标准[1]，进而可以更精确地判断该解决方案是否是解决给定问题的最佳解决方案。此外，机器博弈具有娱乐性，并且对娱乐行业的重要性日益增加，这一事实促进了人们对该领域的进一步研究。

机器博弈研究已经取得了许多显著的成果，比如著名的深蓝计算机，这是第一台击败人类象棋冠军的计算机[2]。然而，对于非完备信息博弈，尚未取得这样的成功。因为这类博弈的状态并不完全可见，意味着存在隐藏的变量/特征。因此，在这类博弈中做出决策更加困难，必须对缺失数据做出预测，这使得获得最佳解决方案几乎不可能。

扑克是一款具有这种性质的非常受欢迎的博弈游戏，因为玩家不知道对手的手牌。计算机扑克的研究在过去几年一直很活跃。人们开发了一些扑克智能程序，但它们都没有达到类似于专业人类玩家的水平。为了克服在先前开发智能程序过程中出现的问题，本文提出了一个新的思路。该方法试图利用现在很火的卷积神经网络来学习人类专家经验进而让程序接近或者达到专业人类玩家的水平。

1 背 景

扑克是数百款具有相似规则游戏的通用名称。计算机扑克研究的重点就是扑克的一种变体——德州扑克，它可能是当今最受欢迎的扑克游戏。德州扑克具有使新开发的方法能够以较少的成本便能运用在其他种类扑克上的特性。

这个游戏是基于玩家打赌他们现在的手牌比对手的手牌要强的想法。整个游戏中的所有赌注都放在彩池里，游戏结束时，手牌排名最高的玩家获胜。或者，也可以通过强迫对手下注他们不愿意比赛来赢得比赛。因此，由于对手的牌是隐藏的，用一只得分较低的手牌赢得比赛是有可能的，这是通过虚张声势——说服对手自己的手牌是排名最高的一只。

1.1 手牌得分等级

德州扑克中，玩家的手牌指的是由定义玩家得分的5张扑克牌组成的牌组。在游戏的任何阶段，手牌等级都是由2张底牌和5张公共牌的组合可能得到的最高得分给出的。可能的手牌等级排行是(从强到弱)：同花顺(同一花色，顺序的牌)，四条(四张同一点数的牌)，满堂红(三张同一点数的牌，加一对其他点数的牌)，同花(五张同一花色的牌)，顺子(五张顺连的牌)，三条(三张点相同的牌)，两对(两张点数相同的牌，加另外两张点数相同的牌)，一对(两张点数相同的牌)，高牌(不属于上面任何一种牌型的牌，由不连续不同花的牌组成，以点数决定大小)。

1.2 德州扑克的规则

德州扑克采用52张扑克牌(除去两张王牌),游戏玩家人数限制在2～9人。在牌局开始时,荷官会给每个玩家发2张“底牌”(只有个人看到),桌面上会分三次陆续发出3张、1张、1张(共5张)的公共牌,在经过四轮的“加注”、“跟注”和“弃牌”等押注圈操作后,若牌局存在至少两名玩家仍然没有弃牌的情况下,进入“摊牌”阶段,在自己的2张底牌和5张公共牌中挑选5张卡牌形成牌组,按照牌型大小规则分出胜负,赢家拿下“彩池”中全部筹码。

1.3 卷积神经网络

卷积神经网络(CNN)代表由卷积层、最大池层和完全连接层的各种组合组成的前馈神经网络，并通过在相邻层神经元之间实施局部连接模式来利用空间局部相关性。卷积层与最大聚集层交替，模拟哺乳动物视觉皮层中复杂和简单细胞的性质[3]。CNN由一对或多对卷积和最大池层组成，最终以完全连接的神经网络结束。典型的卷积网络结构如图1所示[4]。

图1 卷积神经网络结构

在普通的深度神经网络(Deep Neural Network，DNN)中，一个神经元与下一层的所有神经元相连。CNN不同于普通神经网络，因为卷积层的神经元仅根据相对位置稀疏地与下一层的神经元相连。在完全连接的DNN中，每个隐藏节点的输入都是通过将整个输入乘以该层中的权重来计算的。然而，在CNN中，每个隐藏层节点的输入都是通过将部分的局部输入与权重相乘来计算的。然后在整个输入空间中共享权重，如图1所示。属于同一层的神经元具有相同的权重。权重分配是CNN中的一个关键原则，因为它有助于减少训练参数的总数，并产生更有效的训练和模型。卷积层之后通常是池化层。

池的作用是使特征在位置上保持不变，并通过池函数概括出卷积层中多个神经元的输出。典型的池函数是max pooling。max pooling将输入数据划分为一组不重叠的窗口，并为每个子区域输出最大值，降低上层的计算复杂性，并提供一种形式的转换不变性。为了用于分类，CNN的计算链以一个完全连接的网络结束，该网络集成了下面层所有特征图中所有位置的信息。

2 相关工作

构建计算机扑克程序的第一种方法是基于规则的方法，它涉及到为给定的游戏状态指定应该采取的操作[1]。以下方法基于模拟技术[1，5，7]，即生成随机实例以获得统计平均值并决定操作。这些方法指导产生了能够击败弱小的人类对手的智能程序。

1951年Johanson[8]在其《非均衡博弈》博士论文中提出纳什均衡理论。自此，计算机扑克研究开始有重大突破，基于纳什均衡的方法出现了：最佳响应[10]、受限纳什响应[1，11]和数据偏向响应[12]。目前，最好的计算机扑克程序Polaris[12]使用这些方法的混合。

其他最近的方法是基于模式匹配[13-14]和蒙特卡洛树搜索算法[14-15]。

与本文方法密切相关的成功工作是文献[16]。它为另一个扑克牌变种——斗地主提供了深度学习方法。这种方法是从地主的角度出发使用卷积神经网络从一定数量的历史卡片信息的基础上，提取出地主的主要特征，并对农民的手牌做出合理的预测。还有Clark等[17]针对围棋问题提出的一种方法。

尽管取得了所有的突破，但目前还没有一种已知的方法能使智能程序在与人类玩家博弈时取得很好的成绩。

3 基于卷积神经网络的估值算法

纵观近几年关于博弈问题的研究，发现多数的研究者使用浅层人工神经网络来预测对手在博弈中的决策行为以此来建立对手模型，从而规避非完备信息博弈问题中搜索空间过大以及部分信息不可获取的难题。本文提出的方法是利用现在流行的卷积神经网络，学习博弈专家的博弈策略，使得估值算法模型得到的估值更加精确和可信。

3.1 网络输入的建模方法

如何对德州扑克棋局状态建模使之能够作为卷积神经网络的输入是一大挑战。与处理图像问题不同，图像本身就是一个三维的矩阵，可以直接作为神经网络的输入，但是德州扑克的棋局状态则不同。因此，我们必须对其进行建模，转换成可以直接输入的形式。

每副扑克牌不包括大小王共有52张牌，分为4种不同花色，分别是黑桃(Spade)、红桃(Heart)、方块(Diamond)、梅(Club)，每种花色有13张牌，分别是2、3、4、5、6、7、8、9、10、J、Q、K、A，可以用一个4×13的矩阵来表示每一张牌。但在实际工程中，为了方便卷积层做卷积，我们将这个矩阵用0填充扩充成一个17×17的矩阵。

如图2所示，在一个三维矩阵的[1,1,8]和[2,1,7]位置填充1，其他位置均为0，这代表牌局开始时，玩家拿到的手牌是黑桃8和黑桃9。

图2 玩家底牌矩阵模型

阿尔伯塔大学的迈克尔·鲍林教授和他的团队曾经对影响扑克决策的因素展开过研究。研究发现，自己手牌的牌值大小、当前场上的公共牌、对手的动作序列(比如是跟注和加注等行为)、当前的博弈阶段、自己对对手手牌的牌值估计、下注金额等因素都会对博弈的决策产生或多或少的影响。本文综合考虑了上述的情况，最终得到一个16×17×17的三维矩阵作为CNN网络的输入。

表1显示了二人德州扑克局面信息建模所得的矩阵的具体信息。

表1 二人德州扑克局面信息矩阵建模详情

3.2 估值算法

博弈是一个状态不断变化的过程。实际的博弈过程中，第i层博弈局面的估值应该是基于第i-1层博弈局面的估值，因此它们的估值应该是相差不大的。基于以上的假设可以推出以下结论：

设S1,S2,S3,…,Sn是博弈初始状态到终局状态的状态序列，其中S1代表博弈开始的时候的状态，Sn代表博弈结束时刻的状态。E(x)为博弈局面的估值函数，即t时刻的估值就是E(St)。在实际的博弈过程中，博弈体很难做到对所有的中间局面进行准确的估值，但可以轻松地确定终局时刻的博弈局面估值。例如可以设博弈终局时刻的估值为：

E(Sn)=1 代表获胜

(1)

E(Sn)=0 代表失败

(2)

第i层博弈局面的估值应该是基于第i-1的。因此，在距离终局的前一时刻的Sn-1的估值可以由下式求出：

E(Sn-1)=γ·E(Sn)

(3)

虽然相邻两个状态的估值相差不大，但也并非是完全相同，因此可以在式中加入一个参数γ满足γ∈(0,1)，用来调整不同的博弈局面的估值。将该公式进行推广，可以得到：

E(St-1)=γ·E(St)t=2,3,4,…,n

(4)

对于人工神经网络来说，在博弈终局时刻的期望输出可以用式(1)或式(2)来表示，在前面的各个时刻，则可以通过式(3)计算出来。

本文认为学习二维模式(花色和牌值)来代表扑克是很有用的。图像识别的成功方法建议使用卷积滤波器识别二维图像中的对象。在文献[18-20]的启发下，本文搭建了一个CNN模型，称为Poker-CNN。文献[20]采用的深度学习模型中所使用的估值网络完全没有做任何局部死活/对杀分析，纯粹是用暴力训练法训练出一个相当不错的估值网络(需要三千万局自我对局)，而本文提出的估值算法模型考虑了局面因素，能很好地降低网络训练所需时间。

3.1节中已经说明了影响扑克决策的种种因素，并对这些因素进行建模最终得到一个16×17×17的三维矩阵作为输入。网络的输出层则应该包含3个节点，分别对应博弈过程中玩家可以做出的3种选择：弃牌、跟牌和加注。

网络中设置三个卷积层：第一个隐层设有32个5×5的卷积核，步长为2；第二个隐层设有64个3×3的卷积核，步长为2；第三个隐层设有64个2×2的卷积核，步长为1。与围棋类似，矩阵中1的位置精确地代表手牌牌值的大小，因此我们必须要保留位置信息，所以本文也舍弃了传统CNN模型中的pooling层。其后再接一个大小为256×1的全连接层，网络的最后一层有三个节点。最后将加权输出输入到Softmax激活函数再归一化，以输出弃牌、跟牌和加注三种行为的概率。网络的最终结构如图3所示。

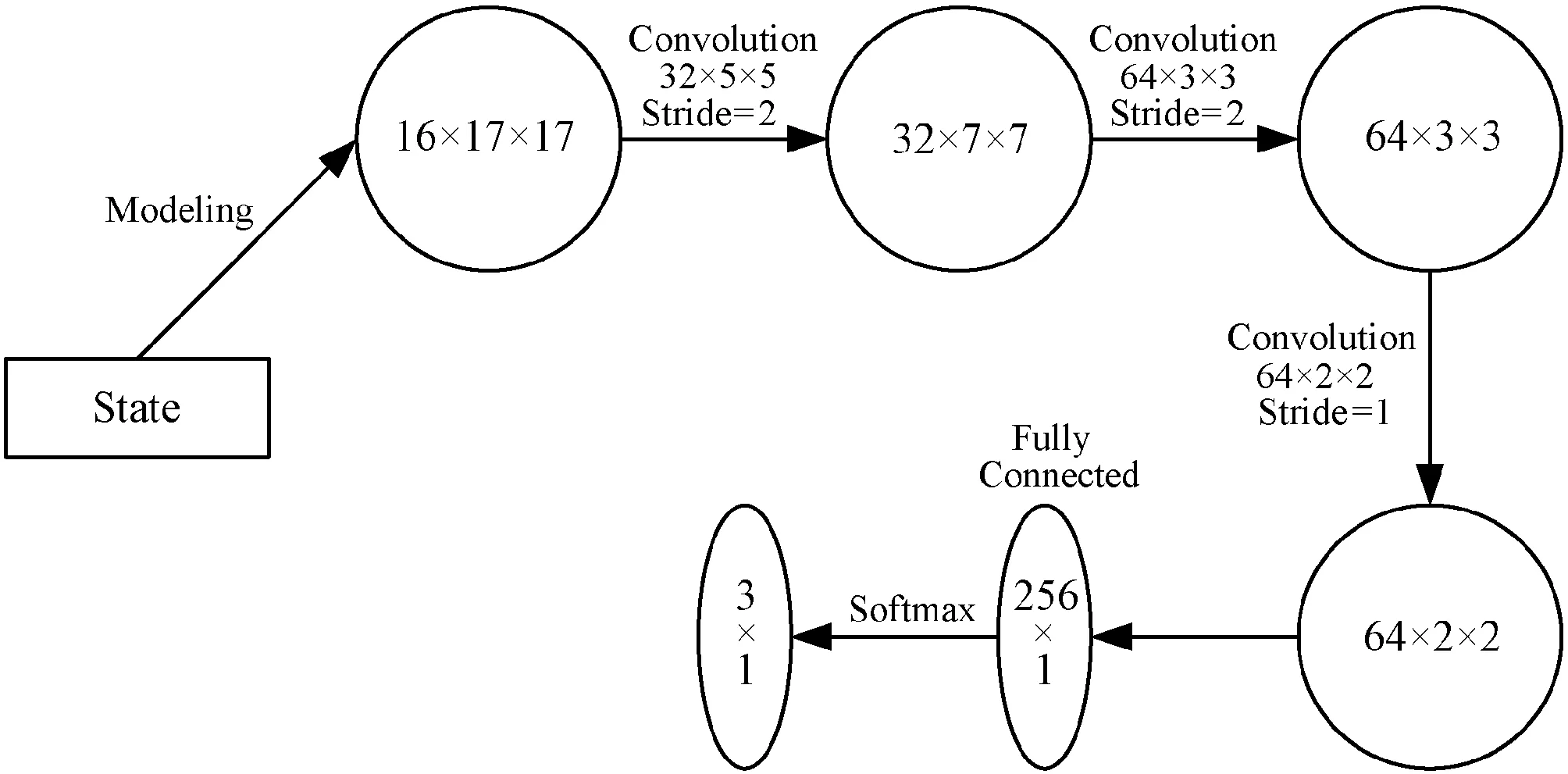
图3 Poker-CNN模型

本文使用ReLU(Rectified Linear Unit)作为卷积层的激活函数。函数形式如下：

(5)

因为网络的输入矩阵是非常稀疏的，所以本文选用在稀疏矩阵中应用较多的Adagrad梯度下降算法。

设定评价函数为E(Si)=max(Y1,Y2,Y3)，它的涵义是取Y1、Y2、Y3三个输出值中的最大值。针对德州扑克，不同的值可以用来代表玩家跟注、加注和弃牌这三个不同动作。神经网络模型采用的是MSRA初始化方法，因为MSRA可以加快网络的收敛。

假设终局局面的状态为Sn，首先根据Sn调整一次网络的误差，然后再根据终局前一时刻Sn-1的估值，计算误差来调整网络权值，逐步反向向前计算，直到学习过程结束。可见，由于要获得终局时刻实际的网络输出，估值算法训练需要在一次完整的比赛记录之上进行。

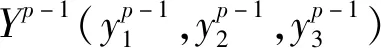
(6)

可以通过的卷积神经网络的不断学习(即修改期望值)来减小该误差，综上所述，可以得出估值算法训练的几个主要步骤：

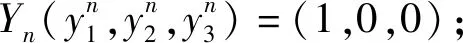
(3) 按照经验初步设置系数γ和学习速率α(训练过程中可以修改)。

(4) 依次计算出隐藏层的输出Cp、实际输出Yn、期望输出Yp的修正量并通过反向传播更新网络连接权值。

(5) 检测学习过程是否结束。若结束则转向步骤9；反之，则继续执行。

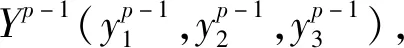
(8) 设p=p-1，转步骤4。

(9) 结束。

4 实 验

4.1 实验环境

表2说明了本文实验的硬件环境。

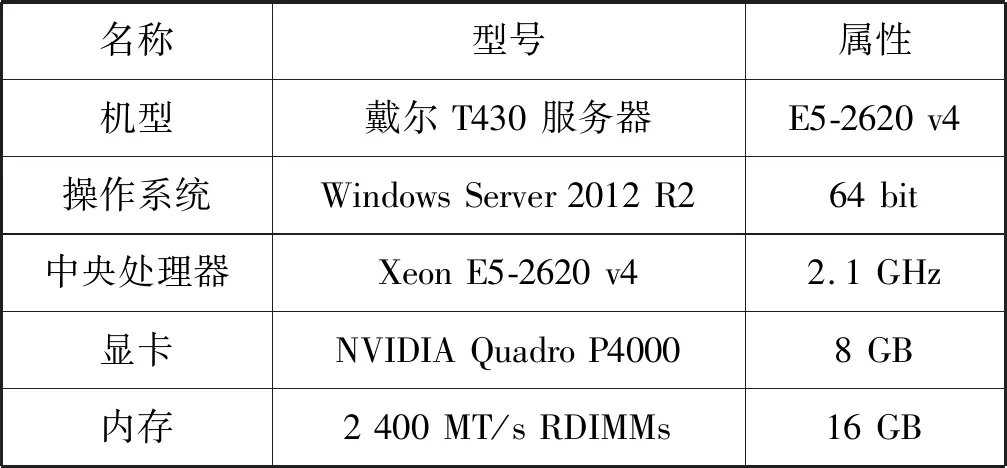
表2 实验环境

4.2 实验数据

美国人工智能会议(AAAI)或国际人工智能联合会议(IJCAI)每年都会举办世界计算机扑克大赛，该比赛吸引了各国的高校及研究机构参赛。他们中的一些竞赛程序具有很高的智能，达到了接近人类大师的程度。

每年比赛的所有比赛数据日志记录，赛事官网都会保留下来并放在http://www.computerpokercompetition.org/downloads/competitions/供大家下载使用。本文下载了2017年世界计算机扑克大赛共2 809 000条二人限制型博弈比赛数据作为网络训练的数据集。

典型的比赛数据如下所示：

STATE:0:cc/cc/cr200c/cr400f:7c4s|2hQh/Ac5h3c/4h/8h:-200|200:Slumbot_ 2pn_ 2017|SimpleRule_ 2pn_ 2017

STATE:1:f:JsTc|5s2d:50|-50:SimpleRule_ 2pn_ 2017|Slumbot_ 2pn_ 2017

STATE:2:cr300c/cc/cr2300f:TcTs|4d5c/5s2dAc/7h:-300|300:Slumbot_ 2pn_ 2017|SimpleRule_ 2pn_ 2017

一条数据表示一局比赛所有的局面状态信息，例如每轮发的牌以及每轮博弈双方采取的行动以及最后的输赢情况。图4简要解释了数据中各项的具体含义。

图4 历史比赛数据格式

对这些日志数据进行清洗，然后写成16×17×17三维矩阵的形式，最后给卷积神经网络作为网络的输入训练该模型。

4.3 结果分析

4.3.1算法预测准确率分析

本文从数据集中随机抽取200 000条数据作为训练集，再在剩余的数据中随机抽取40 000条数据作为测试集对网络进行训练。将训练集分成4个子集，每个子集50 000条数据，对网路作交叉训练。选取下式作为结果的准确率计算方法：

(7)

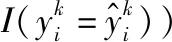
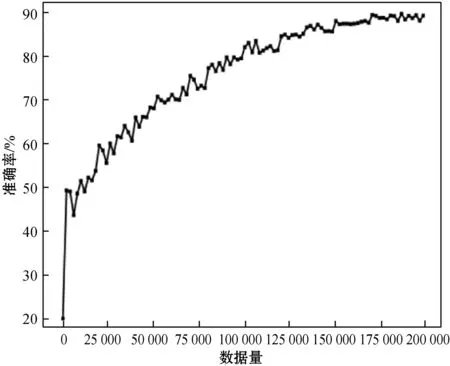
图5 估值算法的准确率

4.3.2智能体博弈结果分析

本文搭建了一个如图6所示的智能体博弈系统，该系统通过Socket通信，服务器相当于发牌员，负责发牌给智能体、判定输赢等。

图6 智能博弈系统

牌局初始化阶段，每个智能体通过特定端口接入到服务器。牌局正式开始后服务器会把牌局各个阶段的信息发送给双方，比如手牌、公共牌、对手是跟牌还是弃牌以及最后的输赢信息。同时，服务器会生成该局对战日志放在log文件夹下。

进行对比测试的其他智能体包括：ACPC官方提供的智能体、基于对手建模算法的智能体[21](获得了2013年ACPC二人限制性德州扑克第四名)，以及基于CFR算法和对手建模的智能体[22](获得2016年ACPC二人非限制性德州扑克第四名)。

为减少实验误差，所有比赛都采用相同的种子，相同的种子玩家获得的牌也是相同的，即输赢完全取决于玩家的策略。

通过分析计算系统日志文件中各智能体的胜负以及输赢筹码数，可以得到图7所示结果。图7给出了本文的智能体与其他3个不同的对手进行博弈时，每局博弈获得的平均奖励(各局的平均奖励用现在手中的总筹码除以当前的局数表示)。

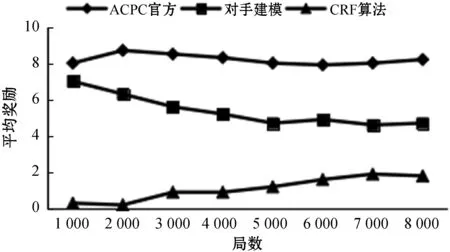
图7 实验智能体与其他智能体对弈每局获得的平均收益

5 结 语

一个完整的非完备信息博弈系统，主要包括五个部分：博弈系统的表示方法、搜索引擎、估值算法、规则解释器、通信系统。估值算法主要作用是评估博弈中每一步的好坏程度，因此估值算法是机器博弈程序的核心与关键。本文主要以德州扑克的二人限制型博弈作为研究对象。首先对牌局的状态进行建模，结合阿尔伯特大学团队对影响德州扑克博弈决策因素的研究，最终得到一个16×17×17的三维矩阵作为估值算法的输入。估值算法模型的核心是卷积神经网络，结合文献[20]的卷积神经网络设计思想与文献[18-19]的研究结论最终得到具体的卷积神经网络模型结构，并用人类大师历史博弈记录来训练该模型。最后将基于该模型的博弈程序与前人开发的博弈程序进行博弈，实验结果显示该模型拥有更高的收益。该估值算法模型为大规模机器博弈系统的实现提供了一个可行的方法，同时为将算法拓展到现实生活提供了可能。

虽然基于人类大师经验的深度神经网络估值算法模型取得不错的成绩，但是该模型还是要依赖人类的专家知识，并且德州扑克每轮的决策与上一轮的决策有关，也就是说决策具有时序性，因此网络模型应该具备记忆性，而本文提出的网络模型没有解决这个问题。克服以上两点是下一步研究工作的重点，可以考虑采用强化学习[23]来减少对于人类经验的依赖以及在不减少模型估值准确率的情况下改善网络结构，同时可以结合循环神经网络或者是长短期记忆网络使网络模型具备记忆性，从而进一步提高博弈程序的性能。