一种基于魂芯DSP的单模式位并行串匹配算法

2020-07-13顾乃杰

计算机应用与软件 2020年7期

陈瑞顾乃杰叶鸿

(中国科学技术大学计算机科学与技术学院安徽合肥 230027)(中国科学技术大学安徽省计算与通信软件重点实验室安徽合肥 230027)

0 引言

串匹配是在已知字符序列(文本串)中按照一定的匹配条件搜索给定字符序列(模式串)集合中元素出现位置的搜索问题，是生物信息学、信号处理和信息检索等方向的核心问题，在涉及字符处理相关领域中具有广泛的应用[1]。随着信息时代数据的高速增长，如何快速高效地处理大规模数据的串匹配问题是当前研究的重点。串匹配问题包括多模式匹配和单模式匹配。其中，多模式匹配的研究大多根据自动机原理，其经典算法包括AM算法[2]、AC算法[3]、FS算法[4]等。单模式匹配是研究串匹配问题的基础，且其他模式匹配算法均由单模式匹配扩展而来，应用领域也最为广泛，已经成为涉及文本和符号处理领域应用的基本组件。因此，研究精确单模式串匹配问题有重要意义。

另一方面，随着多媒体技术的飞速发展，DSP处理器以其低功耗和高性能等特点在信号处理和图像检索等领域有着重要的应用。高性能DSP处理器不仅拥有强大的计算能力，还具有多种先进技术，单指令流多数据流(Single Instruction Multiple Data,SIMD)、超长指令字(Very Long Instruction Word,VLIW)等特殊的硬件结构使得字符串匹配算法在DSP上得以并行处理。本文提出一种基于魂芯DSP的精确单模式位并行串匹配算法，并在平台上进行仿真实验。

单模式串匹配算法众多，代表性的有按照前缀匹配规则的KMP算法[5]、Shift-Or/And(SO/SA)算法[6]和按照后缀匹配规则的Horspool算法[7]和SBNDM2算法[8]。KMP算法第一个在线性时间解决了串匹配问题，该算法利用已经匹配的已知信息，实现无回溯的字符比较，具有线性时间复杂度。Shift-Or/And算法是一种最基础的位并行算法，实现线性的串匹配过程，串匹配速度远快于KMP，该算法维护一个字符串的字符集合，然后利用位操作的内部并行性，实现非确定性有穷自动机(Non-deterministic Finite Automaton,NFA)的全部状态转移。按后缀规则匹配的Horspool算法是简化了的BM(Boyer-Moore)算法[9]，是一种以空间换时间的“跳跃式”匹配算法，在实际应用中比BM算法具有更好的性能。SBNDM2算法在英文语料或者大字符集下搜索具有较高的性能。1985年Galil[10]研究了一种基于软件的并行串匹配算法，可以在O(log2m)时间复杂度下完成串匹配过程，m是模式长度。该算法的缺点是只适用于对固定字符集进行串匹配。同年，Vishkin[11]改进了Galil提出的并行算法，使其支持字符集可变的情况。戴正华[12]从计算机体系结构的角度出发，基于Shift-Or算法通过组合NFA状态，降低自动机状态转换的次数，提高匹配效率，在不考虑Cache失效的情况下，算法比较次数可减少一半。对于并行串匹配算法，随着近些年DSP、GPU和FPGA等硬件的高速发展，把经典算法移植到硬件平台上以提高匹配效率成为研究的热点。侯淼[13]基于GPU高性能并行架构，把经典的AC算法移植到GPU平台进行加速，设计实现了数据并行的PAC算法，并取得了显著的加速效果。Irwin等[14]实现了基于FPGA的并行串匹配算法，相比软件实现方式，算法性能得到显著提升。但该方法由于硬件限制，不易操作，难以广泛应用。李璋等[15]将串匹配算法在CPU、GPU、FPGA上进行了性能的测试与对比，并在GPU上充分利用SIMD结构对算法并行化，在FPGA上利用大量内部逻辑运算单元，实现了高效的串匹配算法。

本文首先通过实验对比了KMP、Horspool、SO三种经典串匹配算法在魂芯DSP处理器上的执行效率；其次结合处理器的分支预测和零开销循环等技术对算法的条件分支语句进行优化，以减少分支语句带来的额外时钟开销；最后结合DSP处理器分簇结构和无漏配的字符串分段方法提出一种基于魂芯DSP的精确单模式位并行串匹配算法EPSO。该算法通过将文本串划分给处理器若干执行簇，减少分簇执行过程中的漏配次数，充分发挥硬件特性，从而有效提升串匹配算法性能。

1 研究背景

1.1 平台介绍

魂芯DSP是国内某研究所自主研发的一款高性能数字信号处理器[16]，可广泛应用于各种高性能计算领域。作为魂芯DSP系列的第二代产品，HXDSP 1042是一款32位浮点DSP，采用哈佛结构、超流水线、超长指令字等并行技术。HXDSP 1042处理器体系结构如图1所示。

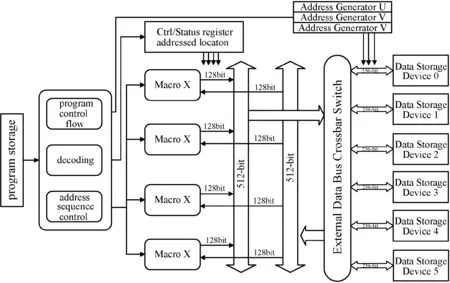
图1 HXDSP 1042体系结构

(1) 内核结构称为eC104+，核内包含4个结构和功能完全相同的执行单元(Element Operation Unit)，分别用X、Y、Z、T表示。每个单元包含128个通用寄存器、8个乘法器(Multiplier,MUL)、8个算数逻辑运算单元(Arithmetic Logic Unit,ALU)、4个移位器(Shifter,SHF)、1个超算器(Super Unit,SPU)。

(2) 处理器含有3个相互独立的地址产生器，分别用U、V和W表示。内部数据总线采用非对称全双工总线，内部数据读总线位宽为512位，内部数据写总线位宽为256位。对于浮点复数而言，支持“两读一写”或“两写一读”，前者是指一个时钟周期每个执行宏读取2个32位浮点复数且写回1个32位浮点复数。后者是指一个时钟周期每个执行宏写回2个32位浮点复数且读入1个32位浮点复数。

(3) 处理器采用VLIW技术，单周期内可并行执行16条共计长达512位宽的指令。条件跳转等分支指令必须排布在指令槽的首部，且每个指令槽至多有一条此类指令。

1.2 相关算法

蛮力算法(Brute Force,BF)是一种最基本的串匹配算法[12]。该算法首先比较模式串的第一个字符和文本串的第一个字符，如果相等，继续比较二者的后续字符；否则，比较模式串的第一个字符和文本串的第二个字符是否相同，以此类推，直到得出匹配结果。该算法本质上是基于模式串前缀规则进行匹配，常见的前缀串匹配算法还有KMP和基于位并行的Shift-Or等，基于后缀进行搜索的算法有BM和Horspool等。下面以KMP、Shift-Or、BM、Horspool算法为例描述各个算法的基本原理。

(1) KMP算法。KMP算法从左至右逐字符地扫描文本串的当前窗口，如果在模式串的位置i处发生失配，则文本串向前移动若干距离，即移动i-fp(i)个字符。其中，fp(i)定义[13]如下式所示，i为0时取-1，否则取最大可偏移的值。

(1)

如果找到一个匹配，则令i=s，窗口向前移动距离为fp(s)，下一个窗口对齐文本串s+i-fp(i)的位置。简单地说，KMP算法记录的模式串前缀，同时也是已经扫描的文本串的最长后缀字符串。图2描述了文本串为“ababcab”，模式串为“abcac”的KMP算法匹配过程。

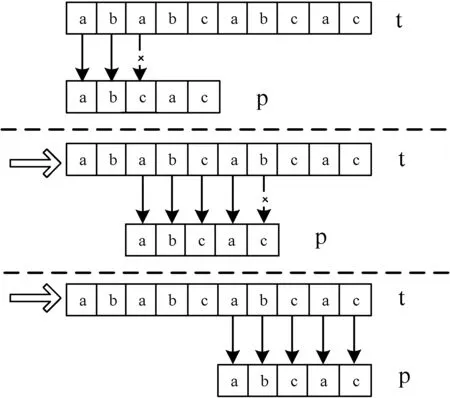
图2 KMP算法匹配示意图

(2) Shift-Or(SO)算法。SO算法和KMP算法类似，也是基于前缀规则进行字符串匹配，但其利用计算机机器字位运算的内在并行性，将多个值装入同一个机器字内，从而加速了串匹配过程。算法1描述了SO算法的基本执行过程，该算法主要维护一个集合D，该集合中保存了所有既是模式串前缀同时又是文本串前缀的字符串。每次读入新字符后，算法利用位并行的方式更新集合。算法中变量B是一个辅助表，也可以称之为字典，其关键字是模式串中的每个字符，值是一个n位的无符号数，记录该字符在模式串p中出现的位置。本文串和模式串分别用t和p表示。假设处理到模式串字符p[i]，则对D进行更新。由于集合D标识了字符p[0…j]是否为文本串t[0…i]的后缀，所以D[j]=0当且仅当更新前的D[j-1]=0且t[i]=p[j]。显然，当D[m-1]值为0时，字符p[0…m-1]是t[0…i]的后缀，找到一个串p的完全匹配。

算法1移位或(Shift-Or，SO)算法

输入：p=p1p2…pm,t=t1t2…tn

输出：[idx1…idxs]

1. //Preprocessing

2. forc∈∑ doB[c]=0m

3. forj∈1…mdoB[pj]=B[pj]&1m

4. //Searching

5.D=1m

6. forpos∈1…ndo

7.D=(D<<1)|B[tpos]

8. ifD|01m-1≠1mthen

9. output ″pos-m+1″

(3) Boyer-Moore(BM)算法。BM算法的基本思想是对模式串从右向左进行逆向匹配，在预处理过程中先构造坏字符表和好后缀表。在匹配时利用坏字符和好后缀规则，跳过尽量多的字符。算法包括两个规则。一个是坏字符规则，假设文本串为t，则从右向左扫描模式串p，若发现某个字符发生失配，则按照两种情况分别讨论。如果当前文本串的字符t[i]在模式串p中没有出现，则直接将模式串向右跳过模式串长度的距离，否则以最右出现该字符的位置进行对齐。另一个是好后缀规则，好后缀表示已经成功匹配的后缀串，共有以下三种情况。

情况一：模式串中存在最左子串和好后缀相匹配，将模式串向右移动，使得子串与之对齐即可。

情况二：模式串中不存在最左子串和好后缀匹配，寻址模式串的一个最长前缀，并将该前缀串等于好后缀的后缀串，然后使两者对齐。

情况三：模式串没有子串和好后缀匹配，并且模式串中找不到最长前缀，移动模式到好后缀的下一个字符即可。

(4) Horspool算法。BM算法简化后得到Horspool算法，该算法基于文本串从后向前匹配时，将主串匹配窗口的最后一个字符和模式串的最后一个字符比较，若匹配成功，则从后往前继续比较；若匹配失败，则根据主串匹配窗口的最后一个字符β在模式串中下一个出现的位置将窗口向右移动，如图3所示。该算法对BM的坏字符规则进行了改进，BM算法的对齐字符是当前发生失配时文本串当前失配字符，而Horspool算法对齐的是文本串匹配窗口的最后一个字符，即字符β，该字符与模式串中最近出现的β对齐。

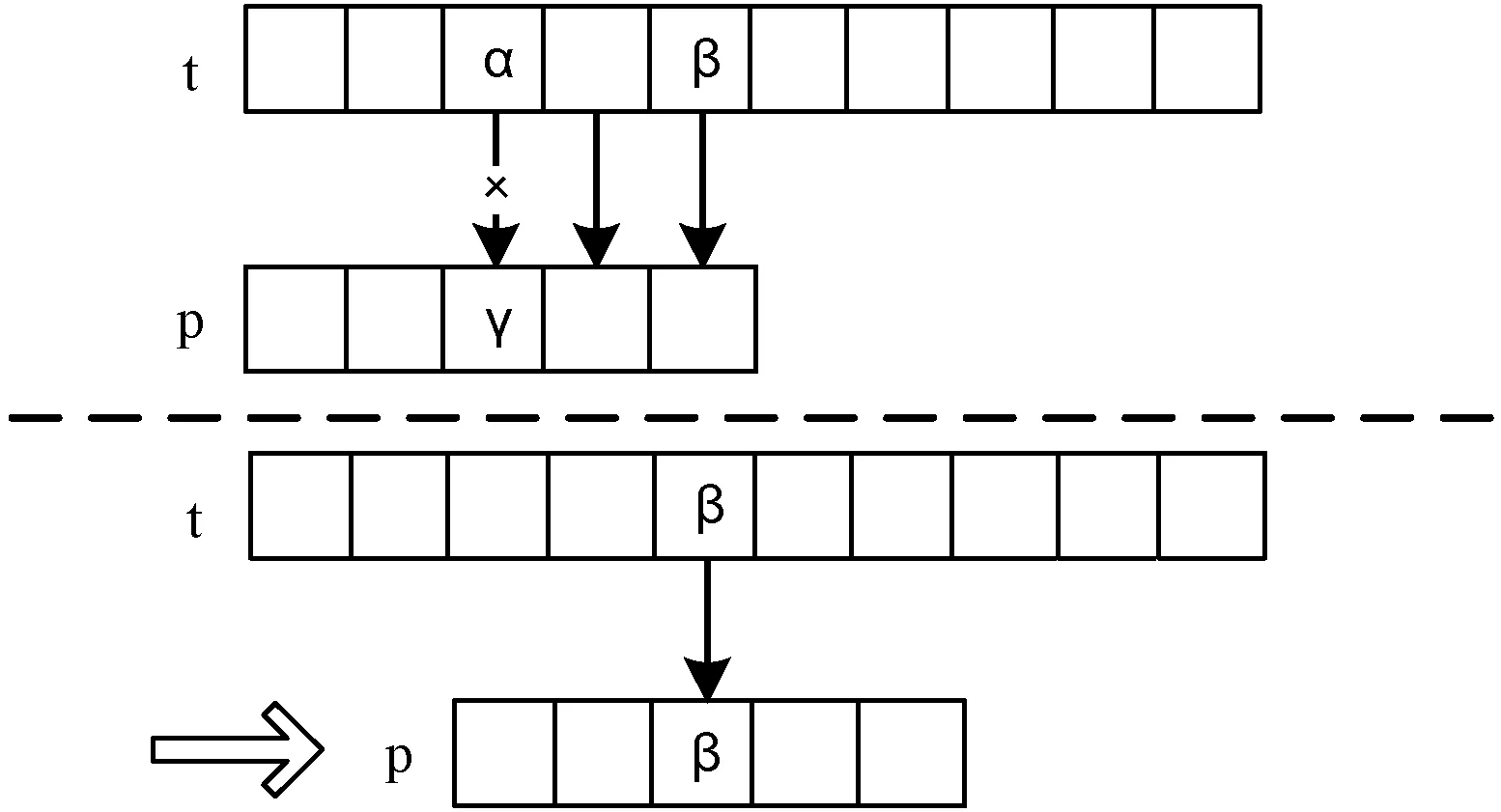
图3 Horspool算法匹配示意图

2 基于DSP的位并行串匹配算法

本节首先通过具体实验对比分析KMP、Horspool和Shift-Or算法在DSP上的执行效率，结合硬件特性讨论各串匹配算法的性能差异；其次利用零开销循环技术对算法的条件分支语句进行优化；最后结合处理器分簇结构和零开销循环技术，提出一种基于HXDSP的高效位并行串匹配算法。

2.1 算法分析

选取KMP、Horspool和Shift-Or三种串匹配算法在HXDSP处理器上进行实验，测试数据为经典字符集Holy-bible.txt[17](176 813个字符)，模式串用随机抽取的方式抽取9个不同长度的串作为测试样本。图4显示了三种算法在HXDSP处理器上的运行结果。

图4 基于HXDSP的串行串匹配算法

测试结果表明，Shift-Or算法和KMP算法性能基本不受模式串长度的影响，针对特定的测试串，其性能基本可以保持稳定；基于后缀规则匹配的Horspool算法不仅性能相对较好，并且随着模式串长度的增加，时钟周期数显著减少。该算法在字符集较大时性能会更好，主要原因在于当模式串长度越大，匹配窗口向前滑动的距离越远。KMP算法作为前缀算法，模式串长度的变化会对算法性能产生一定的影响，主要是因为文本串向前移动距离的不同导致时钟开销出现一定差异。基于位并行的前缀匹配SO算法，由于匹配过程包含大量位运算，并且每一次通过采用位运算的方式进行比较，完成的任务量和模式串长度不相关，因此该算法的时钟周期基本保持稳定。

串匹配算法的性能和处理器硬件结构密切相关。从硬件层面出发，为了提高算法性能，需要尽可能多地或者尽可能早地执行指令。SIMD是高性能处理器的一个重要特性，该技术通过增加指令中完成的操作数，减少完成任务或程序所需要的指令来提高处理器性能。这使得在高性能处理器上加速串匹配算法成为可能，对于上述三种串匹配算法，由于KMP和Horspool算法在匹配过程中是根据一定的规则跳过若干字符距离来提高串匹配效率，若采用数据并行策略，将划分好的文本串交给不同的函数单元进行同时匹配，算法将不能利用SIMD技术的优势，并且会导致无法同时做同样的匹配操作。对于位并行的Shift-Or算法，其核心思想是通过更新掩码集合D来记录模式串的前缀匹配情况，这种匹配过程能够很好地应用在SIMD结构中，采用分治的思想通过将划分好的文本串同时在DSP处理器的四个簇中并行执行，能够更好地利用HXDSP的硬件资源，充分发挥处理器的计算能力，从而加速串匹配过程。

2.2 算法实现

上述串匹配算法中，基于位并行的Shift-Or算法在高性能DSP处理器中能够通过分簇结构更好地将算法并行化。下面首先从HXDSP指令级优化层面对串行代码进行优化，再采用分治思想提出合适的字符串分段方法对算法实施并行化，最后提出高效的基于位并行的EPSO算法。

分析算法1的循环部分，其中针对辅助表B的预处理部分耗时可忽略不计(文本串长度达到一定规模后)，时钟开销主要集中在更新集合D过程中，即算法1的第6行至第9行的循环体部分。从指令层面对算法1进行优化，包括计算开销和条件分支开销。针对计算，除了尽可能提高指令行的并行处理能力之外，需考虑流水线的数据相关。算法1中的D进行更新过程中的移位操作、或操作串行性强，无法利用循环展开的方法来减少运算过程中的流水线停顿，即循环体内涉及串行运算的时钟开销已经没有更多的优化空间。反观条件跳转部分，由于每一次循环都要产生额外的10个时钟周期，算法1的第8行判断是否找到一个成功匹配同样是条件判断操作，同样需要产生一定的时钟开销，相比运算部分，这两个条件判断所占用的时钟周期是运算部分耗费时间的两倍，采用分支预测可以有效提高条件判断和条件分支语句的执行效率。

算法2优化条件分支语句。

HXDSP 1042处理器提供如下两条指令：

指令1：if {x,y,z,t}Rm[bit]==0/1 b

指令2：if lc0/nlco b

上述指令在串匹配算法的条件分支语句中具有重要作用。指令1表示寄存器Rm的第bit位为0或1时跳转至pro处，该指令简化了算法1第8行成功找到匹配点的过程，省去掩码计算过程和掩码与集合D的或非操作，由于该过程在算法1的串行版本下耗费4至6个时钟周期，循环体内计算过程以及条件分支判断总的耗费时钟周期为40左右，因此该指令可以减少算法10%～15%的时钟开销。指令2是基于LC0和LC1寄存器的分支指令，预测机制较为特殊，该指令在取指时读取LC0和LC1寄存器的值，并以此作为是否分支的判断依据。该指令同样能在每个循环体内减少8个时钟开销左右，带来20%左右的性能提升。

为了发挥HXDSP四个簇的计算能力，针对算法2考虑四路并行化，提出一种字符串分段方法以提高计算资源和带宽使用率，进一步提升串匹配效率。并行化的基本思想是将长度为n文本串平均分成4组，对于不能整除的用空字符填充，记为Ti(i=1,2,3,4)。将四组长度相等的文本串分别和模式串P匹配，实现文本匹配过程的并行处理。分段方法的关键在于子文本串在相邻处有可能出现遗漏现象，由于在各段子串的连接处有可能存在和模式串相等的串，因此在将各子串分给不同的执行簇时有一定的概率出现漏配问题。为了避免漏配，有以下3种解决方案。

(1) 由于四个簇并行执行，那么分配给四个簇的文本串长度要保证一致。为了解决相邻子文本串的漏匹配问题，考虑为每个簇分配长度为n/4+m-1的串。

T{x,y,z,t}=Ti+m-1i=1,2,3,4

(2)

式中：T{x,y,z,t}表示分配给每个簇的字符串，m是模式串的长度，字符Tx{n/4…n/4+m-1x,y,z,t}表示簇X文本串的后m个序列，该序列由T1的最后一个字符和T2的前m-1个字符组成。Ty则由T2和T3的前m-1个字符组成。Tz同理，Tt则不同，除了包括T4之外，需要额外补充长度为m-1的字符，如图5中长为m-1的区域，以保证四个簇的文本串长度一致。

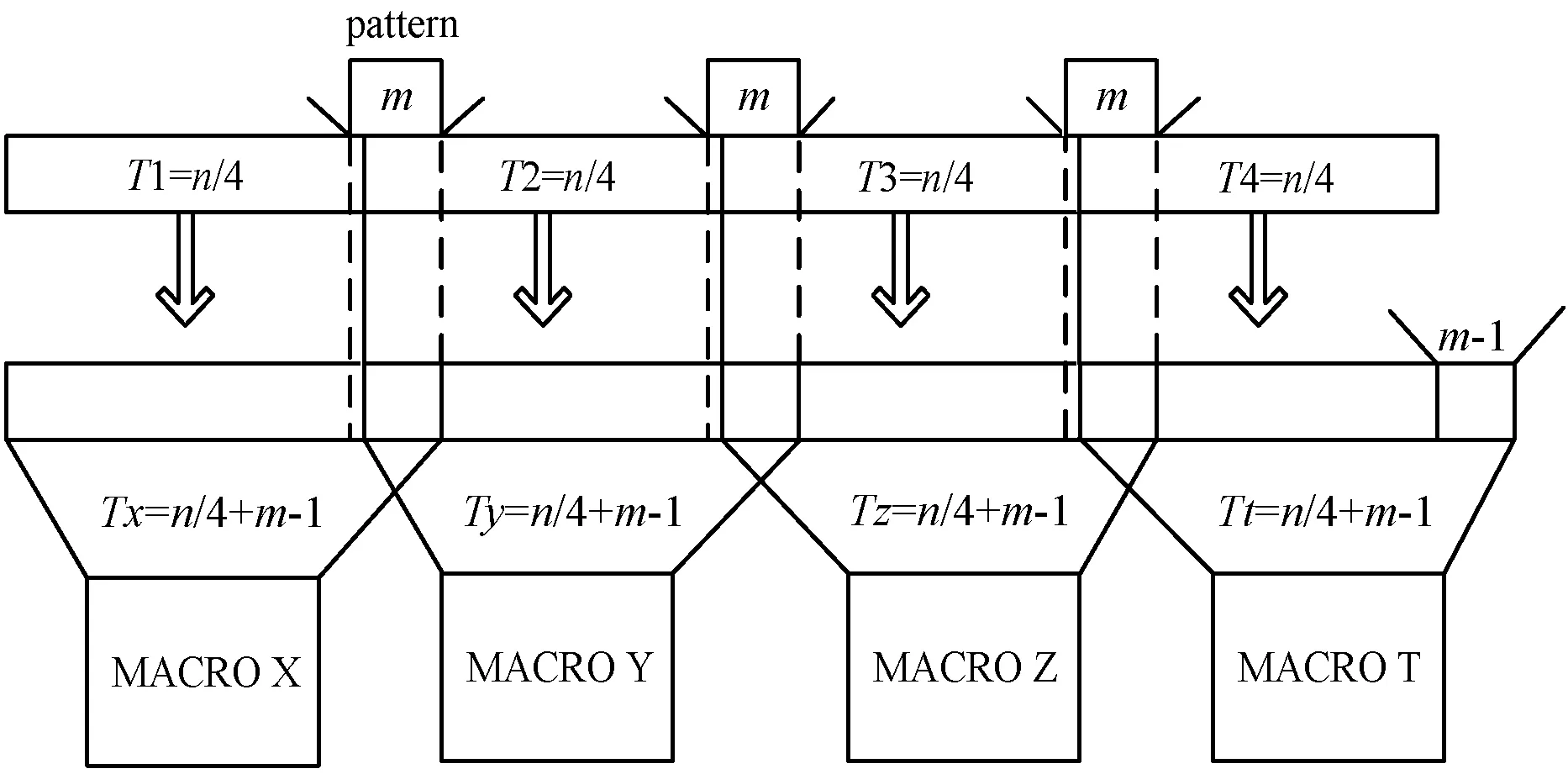
图5 基于HXDSP的并行串匹配过程

(2) 针对Tt文本串改进，将Tt的起始位置向前回溯m-1个字符，如图6所示，尽管这样Tt的匹配和Tz的匹配存在m-1次的重复匹配，但硬件资源充足情况下，省去补充字符的过程，简化了Tt的匹配过程。

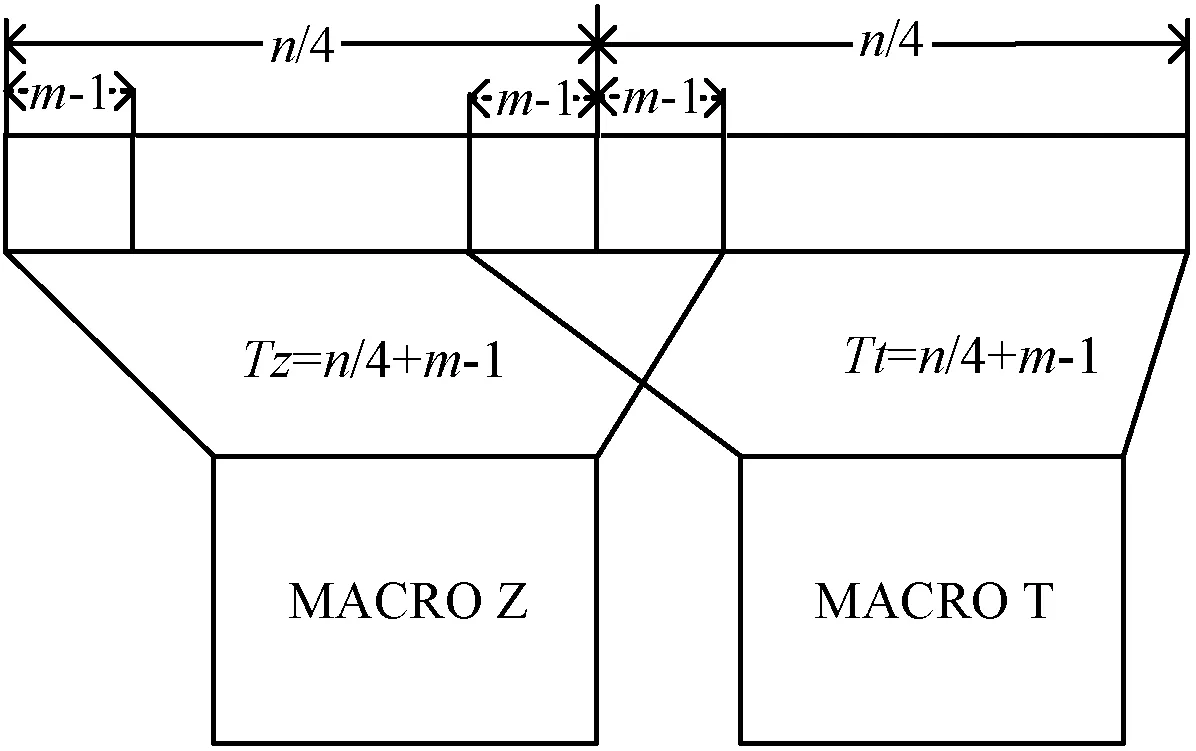
图6 簇T上串划分的改进方案

(3) 由于Tt额外重复匹配了m-1次，考虑继续对方案二进行优化，把该m-1次重复匹配均匀地分配给其余三个执行单元，即每个簇需要匹配的字符减少了(m-1)/4个，如下式所示：

T{x,y,z,t}=Ti+3(m-1)/4i=1,2,3,4

(3)

由于基于位并行的SO算法受字长限制，长度m往往小于处理器字长(32或64)，文本串在一定规模时，这种优化带来的提升几乎可以忽略，并且该方案对m的取值敏感，当m-1不能整除4时，依然需要补充额外字符，这种优化策略导致的额外时钟开销远大于其带来的性能提升。

综上所述，结合处理器的分簇结构和上述分段方法，可有效提高串匹配算法效率。在算法2的基础上按照上述方案(2)的划分方法，提出一种有效的并行移位或串匹配算法，称之为EPSO，伪代码如算法3所示。该算法对文本串的拆分存在4无法被n整除的现象，会导致1～3个串出现漏匹配的问题。为了解决该问题，采用方案一，在文本串text末尾补充e个空字符，其中e=4-n%4，然后按照上述算法进行并行化，匹配完成时为了消除补充字符对串匹配结果的影响，记簇T中成功匹配点为p，忽略p>|n/4|-n%4的设置辅助表B和匹配过程中用于更新的集合D，用本节介绍的字符串分段方法结合处理器的分簇结构把经过预处理的串传输给不同的执行簇，分别按照位并行的方式对D进行移位或计算，最后采用算法2中的条件判断指令分别输出四个簇的成功匹配点。

算法3高效位并行算法(EPSO)

输入：p=p1p2…pm,t=t1t2…tn

输出：[idx1…idxs]

1. //Preprocessing

2. forc∈∑ do {x,y,z,t}B[c]=0m

3. forj∈1…mdo {x,y,z,t}B[pj]=B[pj]&1m

4. //Searching

5. {x,y,z,t}D=1m‖i1=1‖i2=n/4+1

6.i3=n/2+1‖i4=3n/4-m+2

7. fork∈1…(n/4+m-1) do

8. {x,y,z,t}D=({x,y,z,t}D<<1)|B[t{i1,i2,i3,i4}]

9. if {x}D[bit]==0 then output ″k-m+1″

10. if {y}D[bit]==0 then output ″n/4+k-m+1″

11. if {z}D[bit]==0 then output ″n/2+k-m+1″

12. if {t}D[bit]==0 then output ″3n/4+k-m+1″

13.i1++‖i2++‖i3++‖i4++

3 实验分析

本文实验基于HXDSP 1042仿真平台[18]，待匹配文本为测试集Holy-bible.txt(703 KB)和E.coli的DNA序列(coli_str_k_12_substr_mg1655,15,2 143 bp)，在文本中随机抽取100个串作为测试样本。为了精确统计串匹配算法消耗时间，实验采用全局寄存器CC0进行计数。为避免磁盘影响实验结果，所有字符串均已读入内存，只针对匹配过程进行计时，测试三种位并行算法不同匹配条件下的匹配效率。

实验选取KMP算法和Horspool算法作为SO、ESO、EPSO算法的对比算法，实验结果如表1和表2所示。数据表明，703 KB大小的英文文本串下，ESO算法的平均匹配时间达到2.855 ms，EPSO算法的平均匹配时间达到0.716 ms，和经典的SO算法相比，加速比分别达到1.96和7.81。当文本串选取拥有152 143个碱基对的大肠杆菌DNA序列时，ESO算法的平均匹配时间达到3.317 ms，EPSO算法的平均匹配时间达到0.834 ms，相比SO算法，加速比分别可达1.94和7.72左右。HXDSP的实验结果表明，基于位并行的SO算法通过在该处理器上的并行实施和优化，在英文语料和DNA序列中均有良好的性能提升。

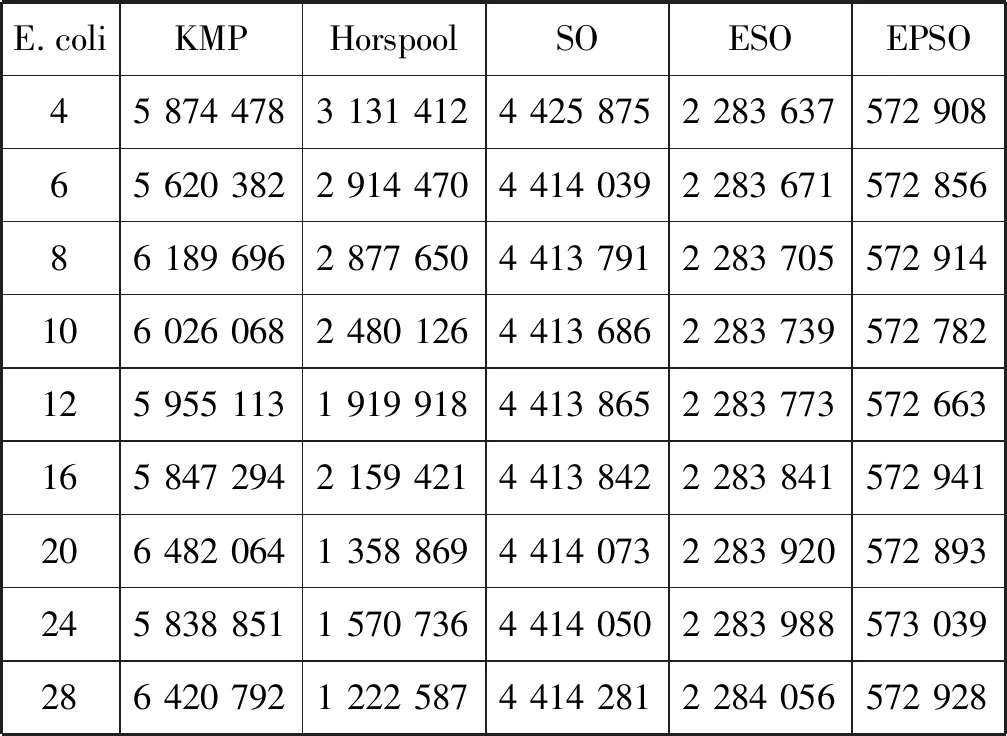
表1 DNA字符集下串匹配时钟开销

表2 英文语料下串匹配时钟开销

为了更好地对比实验结果，将本文算法与范洪博等[20]在Intel E2160处理器上的串匹配工作进行比较。一般来说，魂芯DSP处理器相比现阶段主流Inter处理器拥有更低的主频和功耗。Inter E2160处理器主频达到2.7 GHz，功耗为65 W，远高于魂芯DSP功耗，两者具有相同的核心数和相当的制作工艺。

本文工作基于单核四路SIMD的魂芯DSP进行，范洪博等基于位并行原理提出S2BNDM算法，并在Intel E2160处理器上进行测试，该算法相比NEW、Horspool、KMP等的性能有明显提升。其中NEW算法在小字符集和长模式下具有显著的优势，在英文语料情况下，算法S2BNDM和S2BNDM’分别在短模式和长模式下具有较高的匹配效率。结果的对比以KMP算法为基准，选取单模式匹配NEW[19]、S2BNDM[20]、S2BNDM’[20]作为对比算法，分别比较上述几种高效算法和EPSO算法相比各平台KMP算法的性能提升情况，对比结果如图7、图8所示。

图7 DNA序列串匹配算法增速对比

图8 英文语料串匹配算法增速对比

结果表明，在DNA字符集下，当模式串长度小于16时，相比KMP，EPSO算法匹配速度快于其他三种算法。当模式串长度大于16时，EPSO算法可带来的性能加速比例略小于NEW算法，且和S2BNDM算法和S2BNDM’算法相当，这主要是因为EPSO算法属于非模式敏感型算法，而其他三种算法在模式长度不同时，匹配过程中跳跃的距离不同，性能也不同。在英文语料下，以KMP算法为基准，EPSO算法带来的性能提升明显高于其他三种算法，EPSO算法的匹配速度是KMP算法的6.5倍左右。根据前文对两种处理器的分析，在各项指标不超过Inter处理器的情况下，基于魂芯DSP的单模式位并行算法EPSO比NEW、S2BNDM等算法表现出更好的性能提升效果。