基于鲸鱼优化小波神经网络的飞行航迹缺失数据预测方法

2020-07-13石旭东姜鸿晔

计算机应用与软件 2020年7期

石旭东姜鸿晔

(中国民航大学电子信息与自动化学院天津 300300)

0 引言

随着民用航空事业的飞速发展，飞行安全问题显得尤其重要。为了保障飞行安全，大量传感器设备和飞行记录设备被安装在飞机上。但是，在飞行试验或者实际运行过程中，由于机载设备的运行环境复杂导致飞行数据存在部分缺失，严重影响了飞行数据的后期维护。因此，对飞行缺失数据的预测是维护飞行安全的重要任务，尤其飞行航迹缺失数据预测一直作为研究热点。

目前关于缺失飞行数据的研究方法大体分为两种：一类是基于整体数据相关性的填补方法，如文献[1]提出的燃油流量缺失数据填补算法和文献[2-3]提出的一种飞行参数缺失数据的预估法均是通过先分析数据样本间的相关性，再建立数学模型实现缺失数据的恢复。另一类是基于神经网络的预测方法，神经网络算法由于具有优良的非线性拟合的优点，一直被国内外学者应用在飞行航迹数据处理中。文献[4]在战斗机空战背景下利用Elman神经网络实现目标机的轨迹预测；文献[5]提出了一种基于贝叶斯正则化方法优化Elman神经网络算法。但是在实际求解过程中，上述算法存在输入参数较多、部分参数无法实时获取和多种参数间差异性较大等问题，由此可能引起航迹预测精度偏低和稳定性较差的问题。

针对以上不足之处，多种群智能优化算法被引入到神经网络中，如粒子群算法、蜻蜓算法和鲸鱼算法等。考虑到非线性航迹对稳定性和快速性要求，本文通过对比实验，最终选择设置简单、调节参数少、优化速度及稳定性最好的鲸鱼优化算法，并用其初始化小波神经网络模型参数。此模型提高训练速度的同时弥补了神经网络中存在的学习效率低和容错性低的缺陷。本文首次将WOA-WNN模型运用到飞行航迹预测中，仅依据历史时刻的空间航迹坐标即可实现缺失航迹坐标数据的精确预测。

1 航迹数据预处理

为了避免因数据格式引起的预测精度偏低问题，本文先将获取的经度、纬度和高度航迹数据信息进行预处理，包括位置坐标转化和归一化处理两部分。

1.1 航迹坐标转换

通常将参心坐标系划分成空间直角坐标系与大地坐标系。考虑到飞行仿真软件产生的航迹数据为大地坐标系下表示的，为了更好地表示航迹空间位置信息，本文先将航迹数据转化为空间直角坐标系，地心作为空间直角坐标系的原点[6]。在数学上，大地坐标系与空间直角坐标系转换公式如下：

(1)

(2)

(3)

式中:B为纬度，L为经度，H为高度，a=637 814 m为椭球长半径，b=6 356 755 m为椭球短半径，e为椭球的第一偏心率。

1.2 归一化处理

为了防止不同的航迹数据的量级差别较大引起神经网络预测误差偏高的问题，在完成坐标转化后还需要对航迹数据进行归一化预处理。数据归一化处理方法有最大最小法、变化法和比例缩放法等。本文采用的是最大最小法，把全部的样本数据都归一化到[0,1]内。其函数形式为：

(4)

完成预测后，预测数据需要反归一化处理，其函数形式为：

vi=(vmax-vmin)·ui+vmin

(5)

式中：vi为输入时间序列，vmin代表训练输入数据的最小值，vmax代表训练输入数据的最大值，ui为归一化后的数据样本。

2 航迹预测模型的建立

2.1 小波神经网络算法

随着人工神经网络的发展，许多领域都引入对神经网络的研究，其中BP神经网络或称误差向后传递神经网络，是普遍被应用的神经网络。根据国外学者提出：对于任何连续函数g：U→R，U∈[0,1]，g可以准确地被前馈神经网络拟合，网络中同一层神经单元内部都不互相连接，而相邻层的神经单元之间则互相连接，经过多次训练，可以接近任何一种非线性函数。

法国研究机构最早提出了小波神经网络，其利用非线性的小波函数代替BP神经网络中隐含层的传递函数，得到收敛速度更快、精度更高的网络性能，因此本文选择小波神经网络作为基础模型，小波神经网络结构如图1所示。

输入层到隐含层的状态空间表达式为：

S(k)=f(w1x(k)+b1)

(6)

式中：S(k)，x(k)分别为隐含层输出向量和输入向量，w1为输入层节点与隐含层节点之间的权值，b1为隐含层节点的阈值。选取Morlet小波函数作为隐含层的传递函数，其表达式为：

(7)

隐含层到的输出层状态空间表达式为：

y(k)=g(w2S(k)+b2)

(8)

式中:S(k)、y(k)分别为隐含层输出向量和输出向量，w2为隐含层节点与输出层节点之间的权值，b2为输出层节点的阈值。选取输出层的传递函数为purelin函数，其表达式为：

g(x)=k·x+b

(9)

考虑到航迹数据的时序特性，同时避免迭代过程中学习时间过长，本文利用历史航迹数据中的前6个时刻的位置预测第7个时刻的位置，映射函数可以表示为：

Pt+6=h(Pt+5,Pt+4,Pt+3,Pt+2,Pt+1,Pt)

(10)

式中:Pt=(xt，yt，zt)为飞机在第t个时刻的空间位置坐标，此时神经网络的输入节点为18个，输出节点为3个。

将预处理后的航迹数据拆分为构建训练样本和测试样本。训练样本和测试样本各自分为输入数据样本和输出数据样本。输入数据样本矩阵Pin、输出数据样本矩阵Pout如下所示：

(11)

(12)

小波神经网络节点个数选择时，为了提高拟合精度，往往设置更多的隐含层节点数。但在输入参数数据相同的情况下，随着网络的隐含层节点数递增，更复杂的网络比浅层的网络具有更好的拟合能力，过多的隐含层节点会导致其过度拟合训练数据中非规律性的数据，而忽略整体规律，从而导致预测精度降低；隐含层节点数过少时，神经网络在训练时无法从样本中提取完全的规律，因此无法很好地描述问题的趋势。然而，关于如何选取隐含层节点数没有准确的公式，本文选取文献[7]提到的一种经验公式作为参考。

(13)

式中：L、j、k分别为隐含层、输入层和输出层节点数，q一般取1～10。下文通过多次试验选择最佳隐含层节点个数。

虽然小波神经网络已被普遍应用，但是，其算法存在一些典型的局限：如对收敛速度慢、网络对初始权值和阈值的选取较为敏感和易落入局部最小等。针对小波神经网络的弊端，国内外学者从不同方向提出了多种智能优化算法，并取得了一定成果，如思维进化算法[8]、粒子群算法[9]，还有近些年较新的优化算法，如飞蛾火焰算法[10]、蜻蜓算法[11]和鲸鱼算法[12]。下节利用优化算法初始化WNN神经网络的权值和阈值参数，再通过神经网络训练实现航迹缺失数据的精确预测。

2.2 鲸鱼优化算法

由于部分改进算法仍存在些许不足之处，2016年，国外学者Mirjalili模拟座头鲸的狩猎过程设计出鲸鱼优化算法(Whale Optimization Algorithm，WOA)。座头鲸利用气泡网包围、捕获和搜寻猎物，其方式如图2所示。

图2 泡网摄食行为

1) 环绕猎物。座头鲸包围猎物的行为用数学模型表示如下：

D=|C*X(M)-X(M)|

(14)

X(M+1)=X*(M)-AD

(15)

式中:M为当前迭代次数，A和C为调节系数，X*(t)为当前鲸鱼最佳位置，X(t)为当前位置，其中A、C表达式如下：

A=2a·rand1-a

(16)

C=2rand2

(17)

式中：rand1和rand2为随机数，a从2递减到0。a表达式如下：

(18)

式中：M为当前迭代次数，Mmax为最大迭代次数。

2) 攻击捕获。座头鲸遵行螺旋式运动方式用数学模型表示如下：

X(M+1)=X*(M)+DPeblrandcos(2πlrand)

(19)

式中：b为螺旋线系数，lrand为(-1,1)之间的随机数。DP表达式如下：

DP=|X*(M)-X(M)|

(20)

同时，座头鲸以减小螺旋包围圈的方式追捕猎物，假定收缩包围机制和更新螺旋位置机制的概率均为0.5，数学表示为：

(21)

式中：p为(0，1)上的随机数。迭代时，由于A在(-a，a)的范围内，如果A的值在(-1，1)之间，座头鲸的下个位置介于当前位置和猎物位置之间，设定当A小于1时，发起捕获动作。

3) 搜寻猎物。搜寻猎物的数学表达式为：

D=|CXr-X(M)|

(22)

X(M+1)=Xrand-AD

(23)

式中：Xr为鲸鱼随机位置。设定当A大于或等于1时，随机确定某个个体，根据其位置来更新其他座头鲸的位置信息，以便更好地寻找到食物。此方法提高了全局搜索的能力。

鲸鱼优化算法步骤详细描述如下：

Step1确定小波神经网络结构；将其均方根误差作为WOA算法的适应度函数。

Step2初始化种群规模大小(SearchAgents_no)、最大迭代次数(Max_iteration)、适应度函数(fitness)、个体维数(dim)、个体上限(ub)下限(lb)等参数，并随机初始化鲸鱼位置。

Step3确定所有个体适应度值，记录最佳个体X*信息。

Step4当i≤Max_iteration时，更新a、A、C、lrand和p。

Step5当p<0.5时，如果A<1，根据式(15)更新当前个体的位置；如果A≥1，则从当前群体中随机选择个体位置Xrand，并根据式(23)更新当前个体的位置。

Step6当p≥0.5时，利用式(19)更新当前个体的位置。

Step7确定当前个体的适应度值，记录最佳个体X*，判断是否满足终止条件，若满足，则转到Step 8；否则返回Step 4重新执行。

Step8输出最佳个体；并将最佳个体解码后作为小波函数的初始权值和阈值。

2.3 误差评价标准

神经网络利用误差从输出层参数向后更新到输入层参数实现反向学习，其目的是使网络模型的实际输出尽可能接近目标输出。考虑到飞行航迹数据为空间坐标形式，本文采用均方误差作为模型训练指标。为了表示预测航迹和真实航迹在三维空间中的偏离程度，采用两者欧氏距离作为误差评价标准，公式如下：

(24)

式中：(x1，y1，z1)为预测航迹坐标，(x2，y2，z2)为真实航迹坐标。

进一步分析预测航迹和真实航迹在x、y、z方向上的偏离程度，采用两者绝对误差作为评价标准，绝对误差是模型输出值相对与真实值相差的绝对值大小，公式如下：

E绝对误差=|T1-T2|

(25)

式中：T1为预测值，T2为真实值。

3 实验仿真分析

算法所在的实验平台为Window 10 64 bit系统，64 GB内存。为了获取飞行状态下的航迹数据库，实验以Flightgear飞行仿真软件产生的航迹数据作为样本，取某段连续时间的飞行航迹作为研究对象，在MATLAB 2018a软件进行仿真验证。利用三个飞行阶段各自前900组航迹作为训练数据样本，最后10组作为测试数据样本，验证WOA-WNN模型的有效性。

本文采用前6个时刻的空间航迹坐标预测下一时刻的航迹坐标，所以小波神经元输入节点个数为18，输出节点个数为3。参考上述经验公式计算得隐含层节点范围为6至15。为进一步寻找最佳隐含层节点个数，本文先对不同隐含层节点个数进行仿真。根据10组航迹点的预测位置和真实位置间欧氏距离作为误差评价标准，同时取10次实验的平均值作为最终预测结果，WOA-WNN模型仿真结果如图3所示。

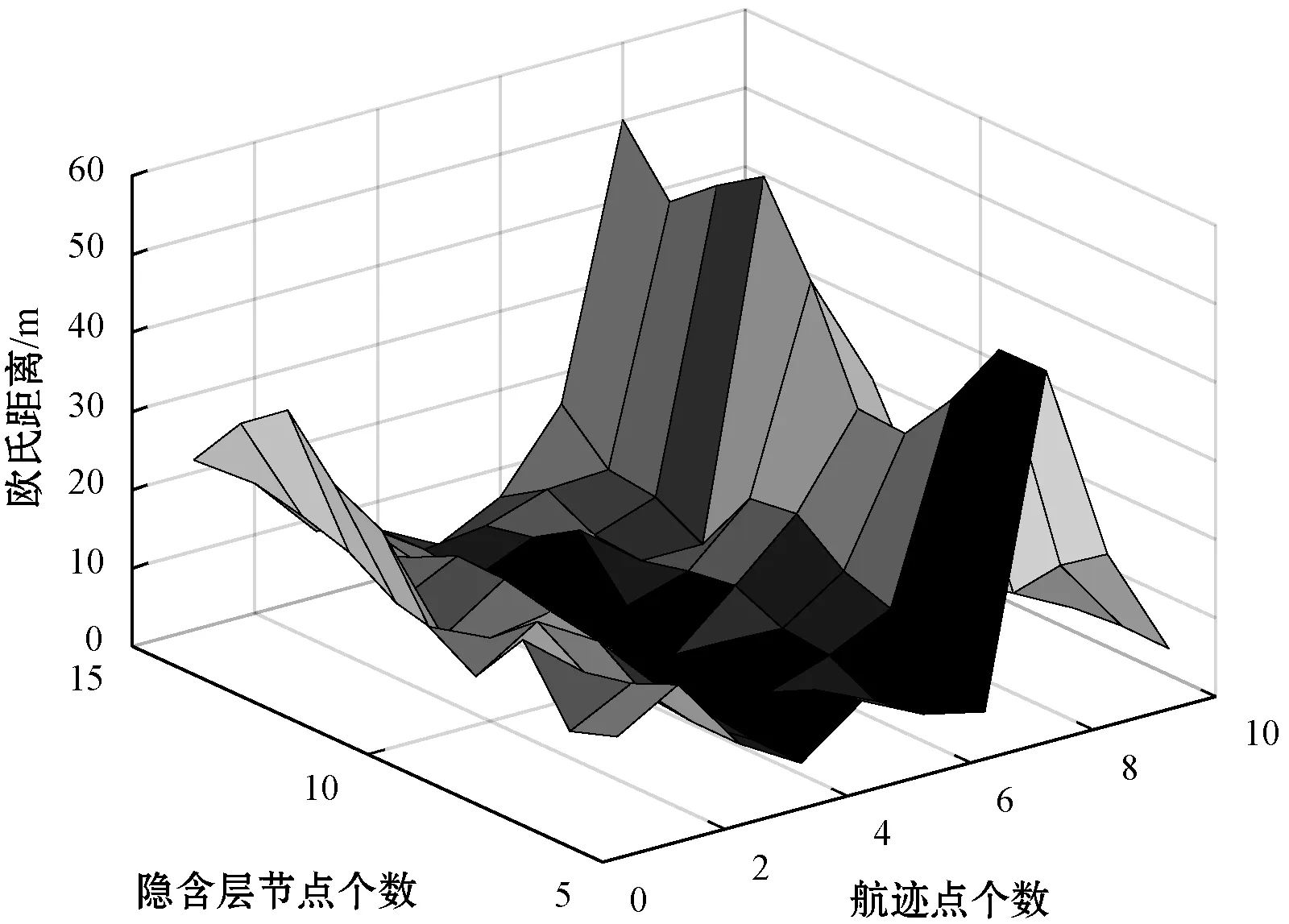
图3 预测误差比较

由图3可以看出，当隐含层节点数为8时，10组测试数据的整体误差最小，因此，WOA-WNN神经网络的隐含层节点个数取8个。根据上文分析得出WOA-小波神经网络结构如下：18个输入层节点、8个隐含层节点和3个输出层节点，每组输入为前6个时刻的x、y、z位置坐标，每组输出为第7个时刻的x、y、z位置坐标。

首先对比多种优化算法的全局搜索能力，初始化PSO-WNN、DA-WNN和WOA-WNN参数：设种群规模为100，最大迭代次数为200，个体维数为18×38+8×3+8+3=719，个体变量的上下限为5和-5。将均方根误差函数作为适应度函数，取10次仿真结果的平均值，适应度变化曲线如图4所示。

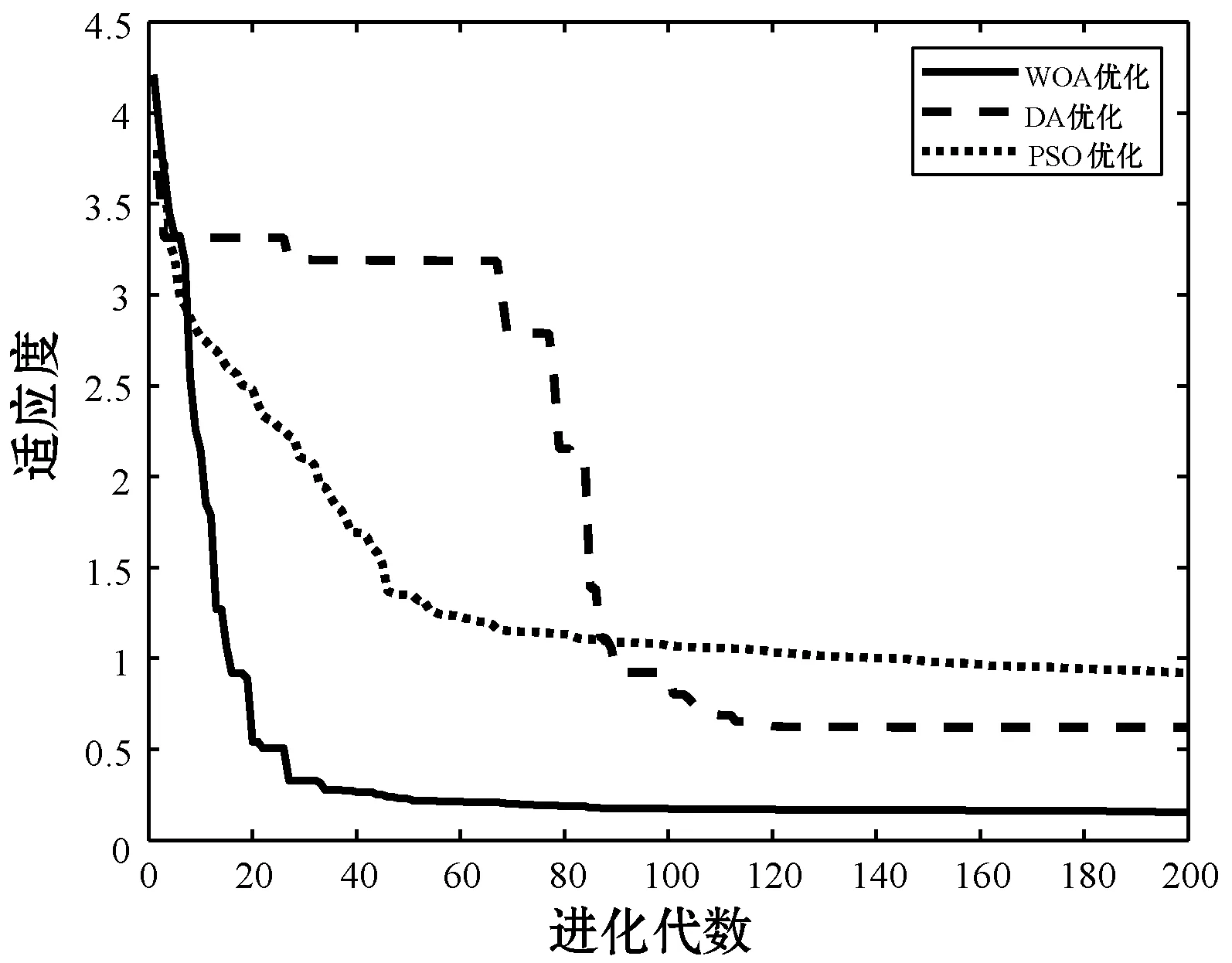
图4 适应度变化曲线

由图4可以看出：随着迭代次数递增，种群逐渐达到稳定。其中WOA适应度曲线下降最快且适应度稳定维持最低，因此其全局和局部搜索能力优于DA算法和PSO算法。再将得到的最佳个体解码作为小波神经网络的初始权值和阈值，利用改进后的小波网络实现航迹缺失数据预测。

为验证WOA-WNN模型在航迹预测中的准确性和适应性，分别对航迹中爬升阶段、巡航阶段和下降阶段进行实验验证。为增加仿真结果的可信度，取10次预测结果的平均值。在空间直角坐标系中，分别在三个飞行阶段对比WNN算法、PSO-WNN、DA-WNN与WOA-WNN算法的预测性能。

爬升阶段预测结果如图5和图6所示。

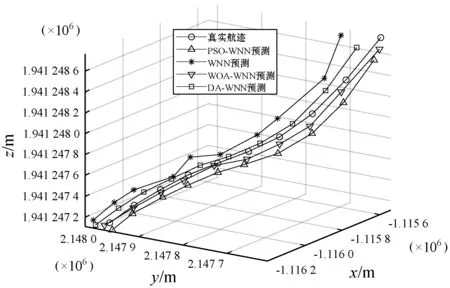
图5 爬升阶段预测结果图

进一步通过预测误差具体分析两者预测性能。先根据10组航迹点的预测位置和真实位置间欧氏距离作为误差评价标准。

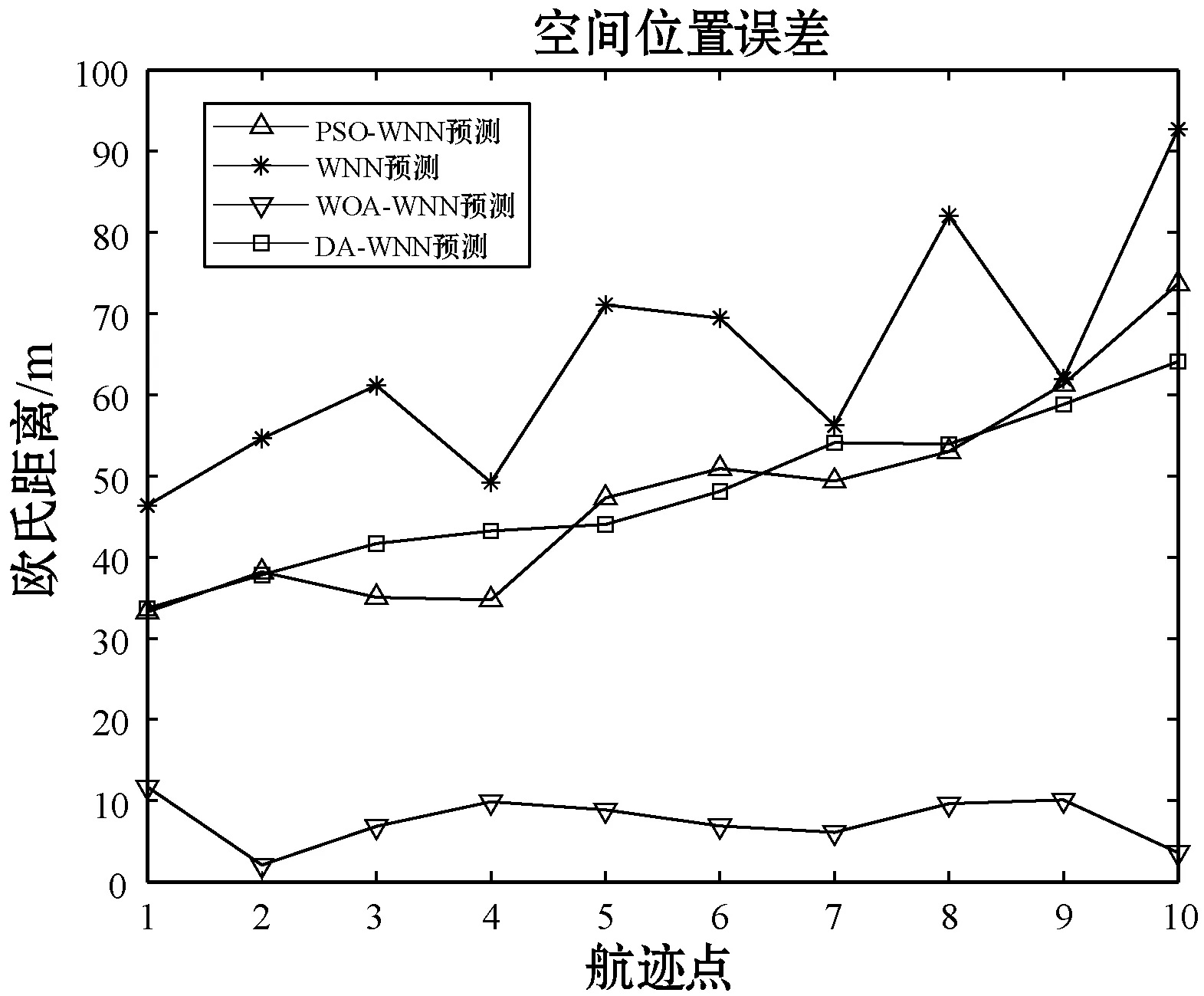
图6 爬升阶段预测误差

采用绝对误差作为评价标准，计算10个预测点x、y、z方向的平均值，结果如表1所示。

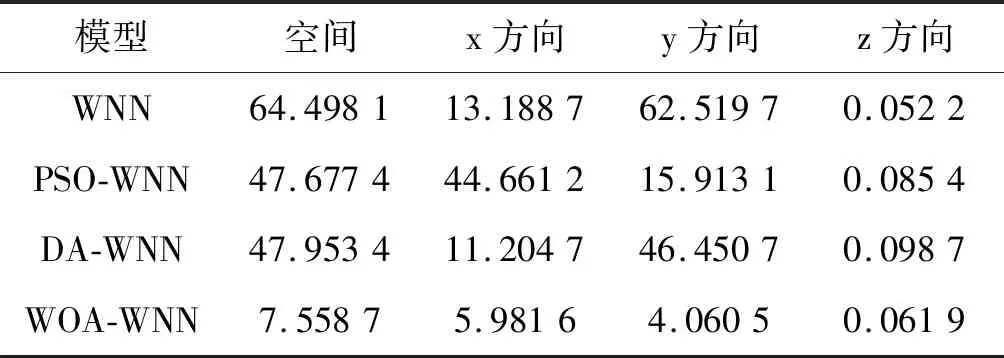
表1 爬升阶段预测误差

巡航阶段预测结果如图7和图8所示。

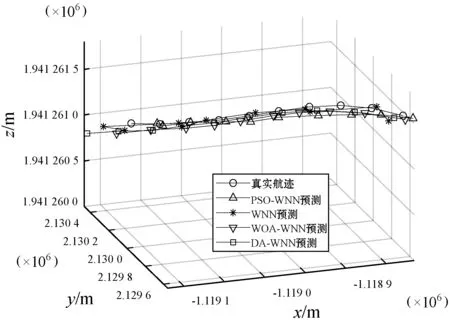
图7 巡航阶段预测结果图

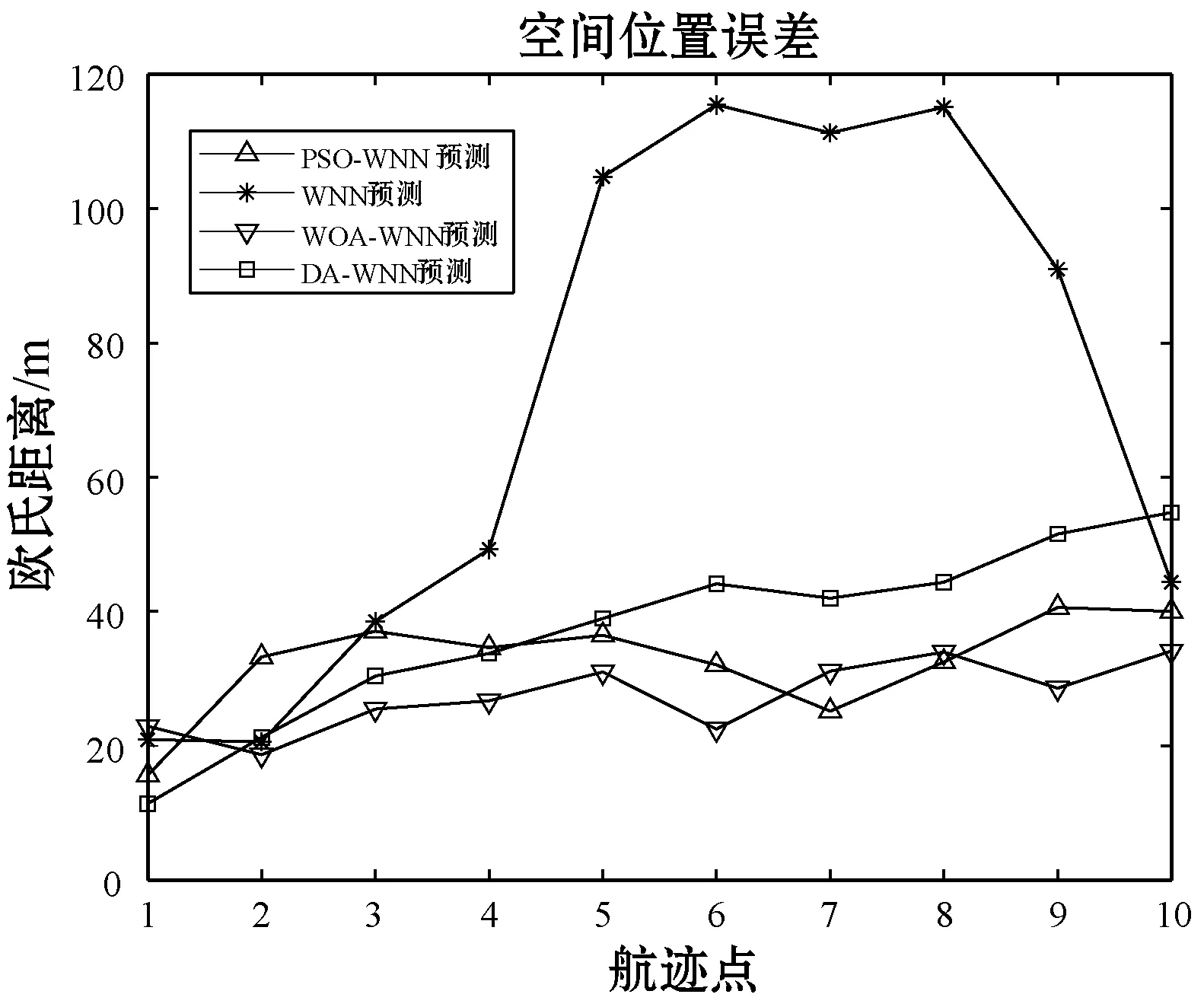
图8 巡航阶段预测误差

计算10个预测点x、y、z方向的平均值，结果如表2所示。

表2 巡航阶段预测误差

下降阶段预测结果如图9和图10所示。

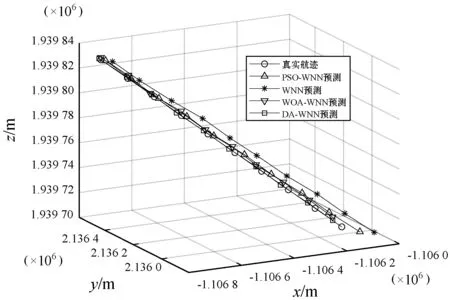
图9 下降阶段预测结果图

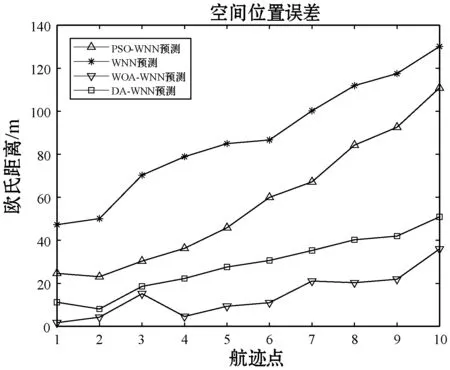
图10 下降阶段预测误差

计算10个预测点x、y、z方向的平均值，结果如表3所示。

表3 下降阶段预测误差

由上述预测结果可以看出，与传统的WNN算法相比，优化算法均可以提高预测精度，增加神经网络的稳定性。其中，WOA-WNN模型预测各个飞行阶段的航迹时都最接近真实值，且预测误差整体相对平稳。因此，WOA-WNN模型可以提高对航迹缺失数据的预测精度，减小预测误差。考虑到飞机自身体积大小，模型的预测性能满足实际要求。