基于遗传算法的灾后物资运输选址与路径优化

2020-07-10周雨晴杨宇晴陈晓阳李晓倩陈金志

读书文摘（下半月） 2020年1期

周雨晴杨宇晴陈晓阳李晓倩陈金志

摘要：本文以云南鲁甸地震相关资料为依据，选取实际的地点作为研究个体，采用遗传算法作为我们的求解方法，对个体的储备物资应急配送进行研究和讨论。在有限的时间、空间、资源等条件约束下，要使应急物资在最短的時间内到达灾区，这就需要充分考虑救援物资的储备地点和运输路径。本文主要考虑时间最短和成本最低两个问题，基于数理建模和实际的限制条件构建双路优化模型，从而选择出最合适的物资储存点和相对最短的运输路径。

关键词：遗传算法;选址;路径优化;灾后物资运输;Matlab

地震是对人类造成最严重危害的自然灾难之一，在我国西部地区（四川、云南等地）强震频发，鲁甸地震的发生给我国的人民带来巨大灾难。在2014年，我国大陆地区共发生5级以上地震22次，6级以上地震5次，集中发生在西部地区。其中，云南鲁甸6.5级地震灾害损失最为严重，是鲁甸地区有历史记载以来的最强地震，造成617人死亡，112人失踪，大量城乡房屋倒损，交通、通讯等基础设施和学校、医疗卫生机构等公共服务设施遭受严重破坏，给当地群众生产生活造成严重影响，直接经济损失201.4亿元（其中云南198.5亿元、四川1.7亿元、贵州1.2亿元）。

储备库选址和路径选优是实现灾后快速救援的核心，而该问题也是近年来国内外学者研究的重点。本文的研究重点是选址—路径两步优化，即在选址优化的基础上对其可能存在的路径进行第二次优化。为此，我们研究了相关领域的优秀论文，探讨其使用的方法和得到的结果。国内学者考虑到应急物资和遗传算法的特点，限制条件的确定是否满足实际情况和数学建模的要求，针对目标函数没有明确的表达式或者在表达式极其复杂的情况，应用遗传算法对变异算子和交换算子等的淘汰方式做了一定深度的研究。何勇指出灾后的应急物资具有突然需要、复杂多变、时间紧迫、约束不一以及需求不确定等特点，很难一次性构建数学优化模型，所以采用了K-均值聚类算法和类子群算法来进行更优的计算。优化可以根据以下两个方面进行：一、不同灾情需求;二、不同约束条件，再进一步计算，分别与物资需求量较小和物资需求量较大两种情况进行有效组合。李清等学者基于最短路问题，考虑到道路的可靠性，构建双目标优化模型，一方面最小化道路起讫点间的长度，另一方面最大化道路的可靠性。采用NSGA-II多目标遗传算法求解，在Matlab软件下进行仿真实验。分别得到三种情形下的解，开展2个目标的Pareto分析，剖析交叉概率和变异概率对结果的影响，有效地解决了最短和最可靠路径的搜索问题。张成元根据选址理论研究的现状和应急救援管理存在的问题，在结合应急物资储备库选址特征的基础上，提出受灾点需求权重问题、选址问题以及储备库分级问题，并分别构建相关模型，给出相应的求解方法。前人已经从震后储存物资选址和救灾路径选优两方面进行了研究分析，给我国的震后救援提供了极大的帮助和参考。

本文基于多个物资供应点的选择和安全最短路径两个问题出发，进行纵向联合研究。通过对我国西南地区灾难频发的地点进行应急资源的优化配置分析，验证模型的可行性和可用性。

1选择研究问题的工具

本文要解决的问题是最佳救灾物资储备库选址及运输路径优化，烦琐复杂的运算程序不利于对实际问题的解决，因此需要科学合理且简单高效的工具辅助研究。考虑到要将问题简单化、运算清晰化、结果可视化，我们在多个应用软件中通过比较界面舒适度、功能多样性和运算精确度，选择界面友好易懂、功能丰富强大、语言较为简单的Matlab软件作为本文研究问题的工具。

2选址-路径优化模型

2.1问题描述

2014年云南鲁甸6.5级地震发生后，根据灾区急需，民政部协调北京、广东、福建3省（市）民政厅（局）向灾区支援5万条毛巾被、5000条毛毯、2.28万套衣服、2500件短袖衬衣、2.4万个手电简和2000件雨衣。截至8月6日16时，云南省共接收社会救灾捐赠款物合计人民币23754.17万元，其中资金14464万元，物资折价9290.17万元。（以上资料来自国家减灾网http：//www.ndrcc.org.cn/）。在应急情况下的物资运输是一项十分艰巨的任务，它考验财力、物力以及人力等多方面的协同工作能力，灾后的物资运输更是需要与时间赛跑。本论文主要研究的是在灾害发生后，如何快速准确的确定从哪个物资储备库最先发送救援物资以及应该在哪一条路径上进行运输，尤其是当一些路径因为自然灾害而不能及时通行时，同时需要做到成本最少，运输最及时。为了实现科学的应急物资运输规划，将选址与路径优化分为两个步骤进行。第一步为选址，第二步为路径优化。应急运输对时效性有一定的要求，在建立模型时应有相应考虑和表达。整个过程有如下假设：

（1）为了避免过多不相关因素的干扰，起点与中转点、中转点与中转点、中转点与终点间的运输距离用两点之间的距离替代;

（2）灾区需求量仅考虑最大化状态，即一个合理固定值;

（3）运输是单向的，即仅由储备库向受灾点运输物资;

（4）运输过程中不损耗救灾物资;

（5）时效性约束用最大允许运输次数来表示;

（6）每一次物资的运输量都等于储备库的最大供给量。

2.2模型构建

目标函数的确定

i为储备库地点编号，s为点编号，n为点的个数。Fi表示第i个储备库建设及运输的固定成本，Vi表示第i个储备库的单位可变成本系数，D表示灾区物资需求量，Si表示第i个储备库的最大供给量，Xs和Xs+1表示相邻两点的x坐标，Ys+1和Ys表示相邻两点的y坐标。minZ表示函数目标是使运输成本最低，运输时间最短。

约束条件分析

（1）编号规则限制

（2）运输次数限制

A为最大允许运输次数，运输次数限制为时效性约束。

（3）个数限制

B为一个固定值，根据实际资料来给定。

（4）算法过程

根据实际资料数据建立一个匹配度较高的坐标图，运用遗传算法解决选址及路径优化问题，使用Matlab软件编写程序进行求解运算。

第一，确定编码。采用四位二进制数的编码方式，将15个点从1到15依次编码为0001—1111，把一条路径用二进制数值来表示，位数长度L=28，表示时不足28位二进制数的，在路径编码中插入合适数量的虚拟点，编码用0000填充，由于虚拟点在实际中并不存在，在计算距离时不予考虑;二进制数超过28位的路径很显然不满足运输时间最短的目标，直接予以剔除。

第二，产生初始种群。根据上述编码，一条路径就是一条染色体，路径上的一个点即为一个基因，利用染色体编码原理生成初始种群。种群规模不宜过大，取M=20～40即可。

第三，用适应度函数对种群个体进行评估。一代种群中的一个染色体即为一个个体，也就是一个可行解，本问题的适应度函数为：

minZ的值越小說明个体的适应性越好，对应的可行解越接近最优解。

第四，选择。选择的原则是优胜劣汰，优秀的个体获得生存机会将基因遗传给下一代。

第五，交叉。指定交换率Pc=0.43。

第六，变异。指定变异率Pm=0.05。

2.3求解结果

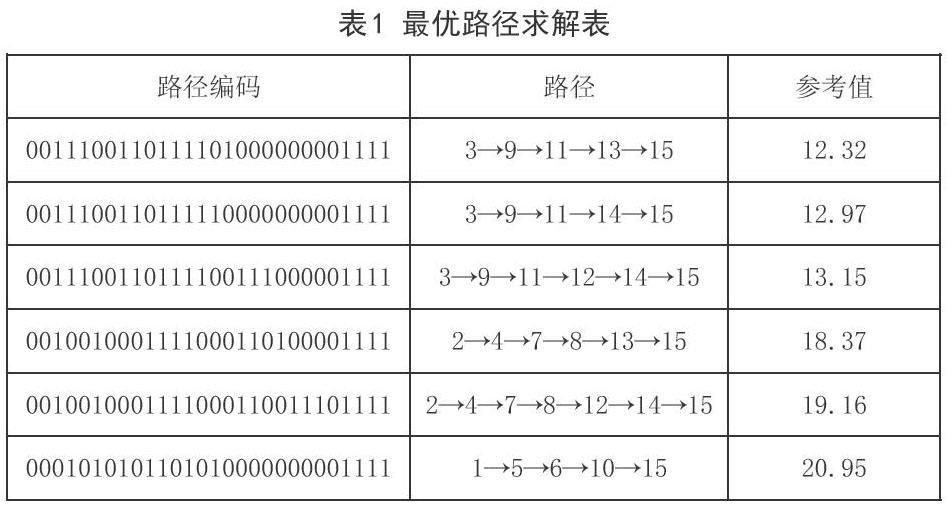
为便于理解和总结用如下表的方式来表达结果：

参考值为考虑问题中多方面因素结合目标函数得出的用于判断结果优劣的数值，路径的参考值越小表明此条路径越优。

由以上图表我们可以得出最佳选址点为图1中的点3，优化后的路径为3→9→11→13→15。通过相关资料可以找到对应的现实地址及运输路径，对应的最佳选址为广州，路径为广州→桂林→贵阳→毕节→鲁甸，此结果具有一定的实际意义。

3结语

本文利用遗传算法对三个储备库（北京、广东、福建）到达灾区路径的横向对比，在已选定的三个运输方案中选出了最佳解决方案，若其他条件满足，可以利用此方案更快地将物资运送到灾区并将受灾人员快速的送到安全位置。