力学模型跷跷板的教学研究

何 敏，江燕燕，祝祖送，吴义恒，尤建村，胡莹莹

（安庆师范大学，安徽 安庆 246133）

0 引言

在日常生活中，跷跷板是一种常见的儿童玩具。初中物理中研究跷跷板的静力平衡问题，适用杆杆原理。本文专门探讨和跷跷板相关的动力学问题。

经过大学力学课程学习，学生通常会将跷跷板默认为可绕定轴转动的一维刚体。实际上，在振动力学中，可将跷跷板简化为两端自由的均匀对称两跨Euler 梁结构，也即我们构造了一种新的弹性体模型。本文主要从刚体模型和Euler 梁模型两个层面对跷跷板进行动力学研究。

文献［1］和文献［2］分别研究了两端自由的Euler 梁离散模型和连续模型微振动的定性性质，文献［3］研究了两端自由的Euler 梁离散模型的振动反问题。因此力学模型跷跷板不仅具有教学研究价值，也同样具有科学研究价值，包括振动的定性性质领域和振动的反问题领域。

1 将跷跷板视为定轴转动的刚体模型

在经典力学教材［4］中，将跷跷板视为绕过中点的轴线转动的一维刚体，设刚体质量为m，长度为2l（为了和下文保持一致）。由定积分运算可知，此刚体的转动惯量为

假设t1时刻刚体的角参量为θ1，角速度为ω1，而t2时刻刚体的角参量为θ2，角速度为ω2，则有刚体的角动量定理（1）式和刚体定轴转动的动能定理（2）式成立：

特例：当两个等体重的人分别关于中点对称地坐在跷跷板的两端，且两个人的双脚都已经离地，则作用于刚体的合外力矩为零。将M=0 无论带入公式（2）还是公式（3），都可以得到ω1=ω2，即角速度ω是常数c，也即公式（1）中刚体的角速度β=0。

2 将跷跷板视为两端自由的均匀对称两跨Euler梁

2.1 Euler梁力学模型的提出

设有一等截面的均匀Euler梁，长度为2l，边界条件是两端自由，梁的中点有一个铰支座，从而构成一个两跨梁。将坐标原点设在梁的中点处，则自变量-l≤x≤l，其横向振动的模态方程是：

其中r(x)=E(x)I(x)是抗弯刚度，E(x)是杨氏模量，I(x)是截面的惯性矩，ρ(x)是密度函数。在本文中r(x) 和ρ(x) 均看成常数。W(x) 是位移振型，λ=ω2A为该问题的特征值，ω是圆频率，横截面积A是常数，x是轴向坐标。

对于两端自由的均匀两跨Euler 梁，有下列边界条件：［5］

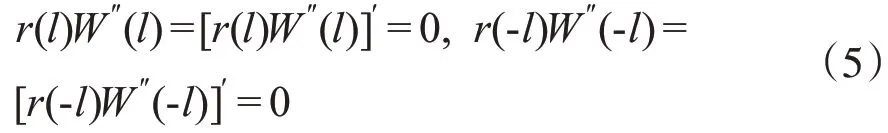
而抗弯刚度为零是没有意义的，因此边界条件简化为

2.2 两端自由的均匀对称两跨Euler梁频率方程和位移函数计算

Euler 梁的无阻尼自由振动满足方程（4），其解为［6］

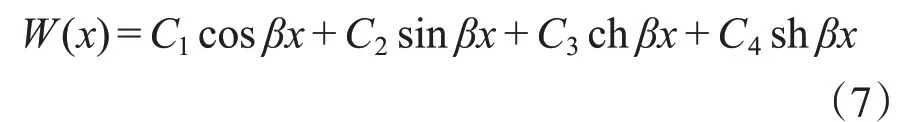
由边界条件可以计算出，两端自由的均匀对称两跨Euler梁的频率方程为

（8）式的结论与文献［6］中铰支-自由梁的频率方程是完全相同的，这是一个超越方程，按照由小到大的顺序，其前四个非平凡解的数值解见文献［6］。前四个非平凡解的近似解为而两端自由的均匀对称两跨Euler 梁的位移函数计算结果为

文献［7］探讨了两端自由的功能梯度梁的一类振动反问题，文中计算得到了两端自由的功能梯度梁的多项式型位移函数，其相对于过梁的中点且垂直于横轴的直线是对称的。结合文献［7］和本文的讨论，可以得出结论：两端自由的对称两跨Euler 梁的位移函数W(x)具有对称和反对称两种模态，且在相差一个常数因子的意义下是唯一的。以上结论与振动力学理论［5］是相符的。

另外，有一种常见的生活用具——扁担，常用竹子或木头制成，也可视为两端自由的两跨Euler梁，但是由于扁担的特殊形状，它不属于均匀梁，因此不能像上文一样得到无阻尼自由振动方程的解析解。顺便指出，将扁担视为悬臂梁是不合理的。

3 结语

对于生活中常见的跷跷板，本文建立Euler 梁模型，将研究对象从振动力学中常见的单跨梁拓展到多跨梁，其计算结果不同于通常的单跨梁结构。

通过本文的研究，学生可以消除思维定式，从弹性体的层面来重新认识跷跷板这一力学模型。从力学思想上来说，弹性体比刚体更加接近物理本源。本文的探讨对于学生力学创新意识的培养是大有裨益的。［8］