多元函数列的一致收敛性及相关极限性质的研究

费时龙，洪佳音，朱少娟

（宿州学院，安徽 宿州234000）

0 引言

常见的分析类教材中讨论了一元函数列一致收敛的概念，这个概念的引入主要目的是在一致收敛的基础上，可以通过函数列自身的连续性、可微性、可积性来研究其极限函数的连续性、可微性、可积性。但是，对于多元函数列一致收敛的概念及相应极限函数的性质却未见涉及，而多元函数列的积分与极限的交换次序的问题无论在理论上还是应用上都是极其重要的，因此，研究多元函数列的一致收敛性及其极限函数的性质有着重要的意义。本文将在一元函数列一致收敛及极限函数性质的基础上引入多元函数列一致收敛的概念并分别讨论其一致收敛极限函数的若干性质。

1 基本概念

定义1.1 设fn(x，y)与f(x，y)为定义在同一平面点集D⊂R2上，若对任意给定的正数ε，总存在正整数N，使得对所有n＞N，及任意(x，y)∈D时，都有

则称二元函数函数列fn(x，y)在D上一致收敛于f(x，y)，记作

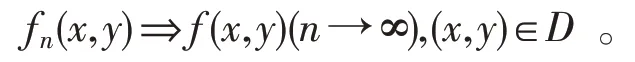
定义1.2 设fn(x1，x2，…，xk)与f(x1，x2，…，xk)为定义在同一点集E⊂Rk上，若对任意给定的正数ε，总存在正整数N，使得对所有n＞N，及任意(x1，x2，…，xk)∈E时，都有

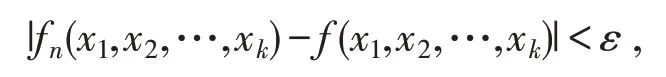
则称k元函数函数列fn(x1，x2，…，xk)在E上一致收敛于f(x1，x2，…，xk)，记作

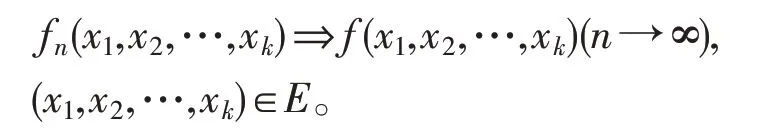
2 一致收敛的判别方法

定理2.1 （Cauchy 收敛准则）二元函数列fn(x，y)在平面点集D⊂R2上一致收敛的充要条件是对任意给定的正数ε，总存在正整数N ，使得对所有n，m＞N，及任意(x，y)∈D时，都有

证明 必要性，设fn(x，y)⇒f(x，y)(n→∞)，(x，y)∈D。则对任意的ε ＞0，存在正整数N ，使得当n＞N时，对一切(x，y)∈D，都有

充分性，由（1）式及数列极限的柯西收敛准则知，{fn(x，y)}在D上任意一点都收敛，不妨记其极限为f(x，y)。现固定（1）式中的n，让m→∞，于是当n＞N时，对于(x，y)∈D，都有

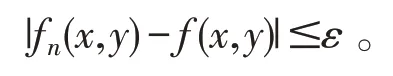
由定义1知，fn(x，y)⇒f(x，y)(n→∞)，(x，y)∈D。

定理2.2 （Cauchy 收敛准则）k元函数列fn(x1，x2，…，xk)在点集E⊂Rk上一致收敛的充要条件是对任意给定的正数ε，总存在正整数N ，使得对所有n，m＞N，及任意(x1，x2，…，xk)∈E时，都有

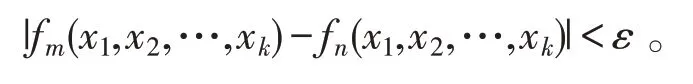
证明 类似于定理2.1的证明。

定理2.3 二元函数列fn(x，y) 在平面点集D⊂R2上一致收敛于f(x，y)的充要条件是

证明 必要性，若fn(x，y)⇒f(x，y)(n→∞)，(x，y)∈D。则对任给的正数ε ，存在不依赖于(x，y)的正整数N，使得当n＞N时，有

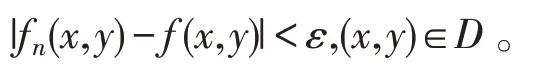
由上确界的定义，亦有

充分性，由假设，对任给ε＞0，存在正整数N，使得当n＞N时，有

因为对一切(x，y)∈D，总有

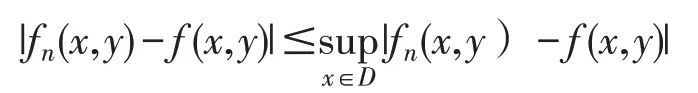
故由（5）得

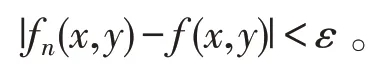
于是fn(x，y)在D 上一致收敛于fn(x，y)。

定理2.4k元函数列fn(x1，x2，…，xk) 在点集E⊂Rk上一致收敛于f(x1，x2，…，xk)的充要条件是

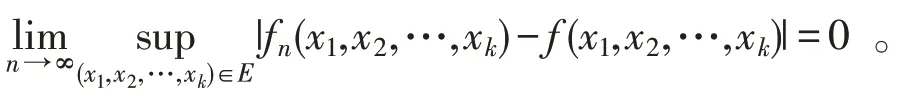
证明 类似于定理2.3。

3 一致收敛极限函数的性质

定理3.1 设fn(x，y)⇒f(x，y)，(x，y)∈D，P0为平面区域D的一个聚点，若对每个n ，极限均存在且

证明 首先证明数列{an}收敛，对任意给定的正数ε＞0，由fn(x，y)⇒f(x，y)知存在正整数N，当n＞N及任意给定正整数p，及任意(x，y)∈D均有

令P→P0，则有

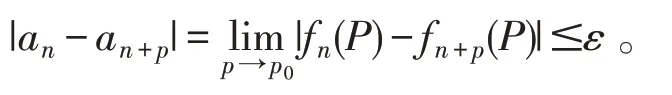
由Cauchy收敛准则知数列{an}收敛。

因此，当0＜|P-P0|＜δ时，有|f(P)-A|≤|f(P)-

注：定理3.1表明：在二元函数列一致收敛的假设下，{fn(x，y)}中变量x与n，在对两个变量分别求极限时，极限的顺序可互换，即

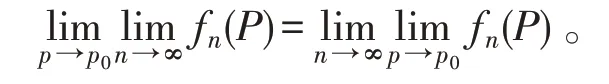
定 理 3.2 设fn(x1，x2，…，xk)⇒f(x1，x2，…，xk)，(x1，x2，…，xk)∈E，P0为平面区域E 的一个聚点，若对每个n，极限则极限

证明 类似于定理3.1。

定理3.3（二元极限函数的连续性）设二元函数列fn(x，y)在二维平面区域D⊂R2上一致收敛于f(x，y)，且每一项fn(x，y)都在D上连续，则极限函数f(x，y)在D上也连续。

证明 设任意Q0(x0，y0)∈D，由fn(x0，y0) 及定理3.1 可得存在，并且故f(x，y) 在 点Q0(x0，y0)连续，由Q0(x0，y0)的任意性知f(x，y)在D上连续。

注定理3.3 表明：若连续的二元函数列fn(x，y)其极限函数f(x，y)不连续，则fn(x，y)不一致收敛。

定理3.4（多元极限函数的连续性）设k元函数列fn(x1，x2，…，xk) 在 区 域E⊂Rk上 一 致 收 敛 于f(x1，x2，…，xk)，且每一项都在E上连续，则极限函数f(x，y)在E 上也连续。

证明 类似于定理3.3。

注：定理3.4 表明：若连续的k元函数列fn(x1，x2，…，xk)其极限函数f(x1，x2，…，xk)不连续，则fn(x1，x2，…，xk)不一致收敛。

定理3.5（二元极限函数的一致连续性）设fn(P)在平面区域D⊂R2上一致收敛，且fn(P)在D上一致连续，则f(P)在D上也一致连续。

证明：因为fn(P)在D上一致收敛，故对任意ε＞0，存在正整数N，使得当n＞N及任意p∈D，有|f(P)-fn(P)|＜ε

又因为fn(P)在D上一致连续，从而对上述的ε＞0，存在δ＞0 ，使得任意p1，p2∈D，只要|p1-p2|＜δ，就有|fn(P1)-fn(P2)|＜ε，从而对上述的ε＞0，存在δ'=δ，当|p1-p2|＜δ'时，令n＞N，则|f(P1)-f(P2)|=|f(P1)-fn(P1)+fn(P1)-fn(P2)+fn(P2)-f(P2)|≤|f(P1)-fn(P1)|+|fn(P1)-fn(P2)|+|f(P2)-fn(P2)|＜3ε，故[f(P)]在D上一致连续。

定理3.6（多元极限函数的一致连续性）设fn(P)在平面区域E⊂Rk上一致收敛，且fn(P)在E上一致连续，则极限函数f(P)在E 上也一致连续。

证明类似于定理3.5。

定理3.7（二元极限函数的可积性）设二元函数列fn(x，y)在有界闭域D⊂R2上一致收敛，且每一项都在D上连续，则极限函数f(x，y)在D 上也可积。

证明 设f(x，y)为{fn(x，y)}的极限函数，则由定理3.3的结论知，f(x，y)在D上连续，故fn(x，y)(n=1，2，…)与f(x，y)在D 上均可积。

定理3.8（多元极限函数的可积性）设k元函数列fn(x1，x2，…，xk)在有界闭域E⊂Rk上一致收敛，且每一项都在E 上连续，则极限函数f(x1，x2，…，xk)在E 上也可积。

证明类似于定理3.7。