同步励磁发电机鲁棒非线性控制

付学敏，程 晨，张永彬，杨辉军，王 辉

（1.安徽新闻出版职业技术学院，安徽 合肥 230601；2.安徽国际商务职业学院，安徽 合肥 230601）

0 引言

随着大型同步励磁发电机的发展、电网规模的不断扩大和系统运行方式的复杂性增强，系统的动态性能对控制作用的要求越来越高，而且同步励磁发电机模型是非线性的，以往的控制策略都是在工作点附近对模型进行线性化，这并不能满足现在的控制要求。设计出高性能的控制器是同步励磁发电机可靠运行的重要保证，研究同步励磁发电机的鲁棒非线性控制具有十分重要的意义［1，2］。

近年来，对于同步励磁发电机的非线性控制问题，已有大量的研究。文献［3］中提出了电力系统的非线性振荡现象及分叉现象，充分解释了电力系统中存在大量的非线性。文献［4］提出的backstepping控制方法对非线性的同步励磁发电机模型设计了控制器，并进行了仿真研究，但在控制器设计的过程中，并没有考虑到可能出现的外部扰动［5］。另外在电力系统非线性控制研究方面，文献［6］给出了电力系统各个方面的非线性数学模型，并详细研究了非线性控制理论在电力系统中的应用。

针对同步励磁发电机系统中可能出现的各种不确定因素以及有界扰动，本文首先给出了同步励磁发电机的非线性数学模型，并且引入了有界的外部扰动，然后给出了输入-状态稳定性（ISS稳定性）以及Lyapunov稳定性的定义，针对提出的同步励磁发电机非线性数学模型设计了一种鲁棒非线性控制器，最后给出了系统从初始进入稳态过程中相对攻角、相对角速度以及控制律的仿真曲线，验证了该控制器的有效性。

1 系统模型

单机无穷大系统的模型为

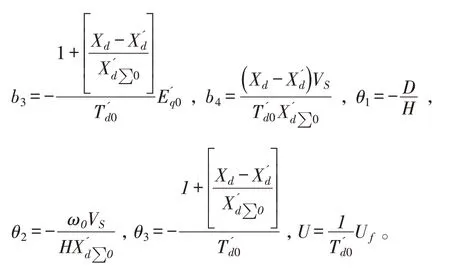
其中ω、ω0分 别代表角速度和同步角速度，δ、δ0分别代表转子运行角和同步转角。D代表阻尼系数，H代表机械转动惯量，Pm代表机械效率，代表同步发电机暂态电势，Uf代表励磁输入，VS代表无穷大总线电压，代表励磁绕组时间常数，分别代表同步电抗、暂态电抗和d轴总暂态电抗，γ1与γ2分别代表外部有界扰动。

由于系统最终要达到稳定工作点(δ0，ω0，E'q0),因此可选择新的状态变量为Δδ=δ-δ0，Δω=ω-ω0，ΔE'q=E'q-E'q0，则系统新的数学模型可写为

令x1=Δδ，x2=Δω，x3=ΔE'q，可得到系统的状态空间模型为

输入- 状态稳定性（ISS）［7］: 对于系统，如果存在一个KL 类函数β 和一个K类函数γ ，使对于任何初始状态x(t0)和有界输入u(t)，解x(t)对于所有t≥t0都存在，且满足

则称系统˙=f(x,t,u)是输入-状态稳定的。

向量范数（‖·‖）［8］:对于任一非零向量X∈Rn，定义我们称‖X‖的范数，鲁棒性（Robustness）［9］:是指控制系统在一定（结构，大小）的参数摄动下，维持其他某些性能的特性。

2 控制器设计

针对系统（3），假设外部干扰有界，即max(γ1,γ2)≤β，其中β 为常数。利用输入-状态稳定性（ISS）设计控制器如下。

考虑同步励磁发电机的三阶非线性模型（3），将γ1,γ2视为有界扰动输入，设计适当的控制律（见下文（10）式），系统（3）对扰动具有输入-状态稳定性；此外，当扰动为零时，系统（3）具有指数稳定性。

证明 选取Lyapunov 函数

计算V 沿系统（3）的时间变化率

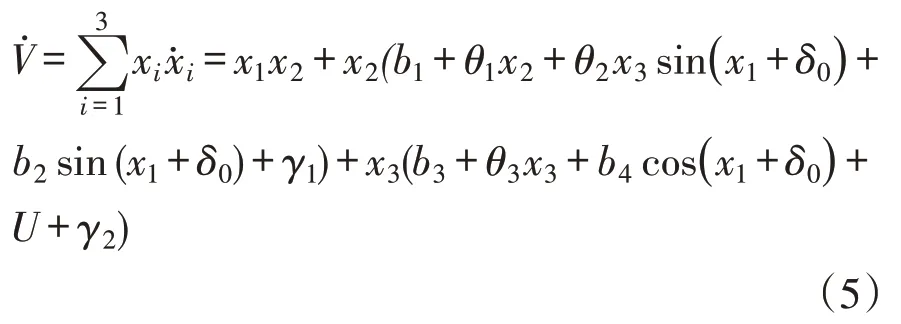
将（6），（7），（8）代入（5）中，可得

因此，可以设计如下控制律

将控制律（10）代入（9）中，我们可以得到

其中，β ≥max(γ1,γ2)，令x3)求解上述常微分不等式，可得

因此，有

因此，我们可以得到在控制律（10）的作用下，闭环系统（3）对于外部有界扰动而言，是输入-状态稳定（ISS）的。并且，在无扰动的情况下，由Lasalle定理［7］可知系统是指数稳定的。因此可知，该闭环系统具有鲁棒性。

3 仿真分析

本文做了系统在有界的外部扰动作用下，从初始进入稳态过程中，转子相对运行角（与稳态时的差值，后面类似）、相对角速度以及同步励磁发电机相对暂态电势的曲线图，同时，给出了本文中控制律的示意图，来验证所涉及控制律的有效性。

在本文中，设定同步励磁发电机的相关参数为

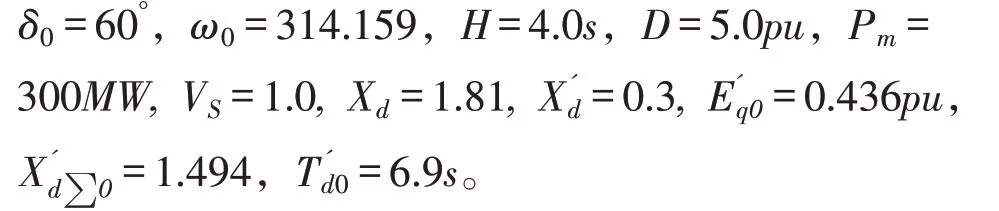
情形（1）：设定扰动上界为β=20，转子相对运行角、转子相对角速度、同步励磁发电机相对暂态电抗以及控制律的仿真图如图1-4所示。

图1 从初始进入稳态过程中转子相对运行角响应曲线

图2 从初始进入稳态过程中转子相对运行角速度响应曲线

图3 从初始进入稳态过程中相对暂态电抗响应曲线

图4 从初始进入稳态过程中所设计控制律响应曲线

情形（2）：设定扰动上界为β=60，转子相对运行角、转子相对角速度、同步励磁发电机相对暂态电抗以及控制律的仿真图如图5-8所示。

图5 从初始进入稳态过程中转子相对运行角响应曲线

图6 从初始进入稳态过程中转子相对运行角速度响应曲线

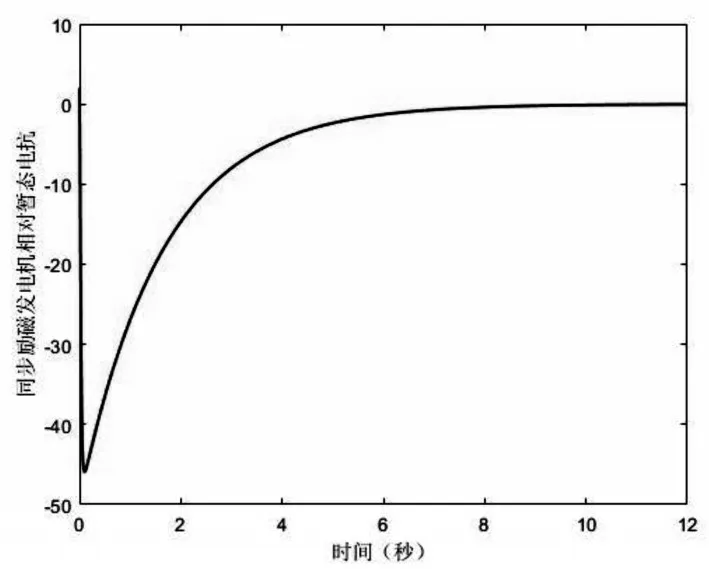
图7 从初始进入稳态过程中相对暂态电抗响应曲线

图8 从初始进入稳态过程中所设计控制律响应曲线

系统从初始进入稳态过程中转子相对运行角、相对角速度、同步励磁发电机相对暂态电抗以及控制律分别如图1-8 所示。可以看出转子相对运行角、相对角速度和同步励磁发电机相对暂态电抗都从一定的初始值，最后收敛到零的邻域内，即达到稳定状态，说明所设计的控制律对外部有界干扰具有鲁棒性。由图4 和图8 可以看出，控制律最后也收敛到零，充分验证了所设计控制器的有效性。

4 结论

本文首先给出了同步励磁发电机的三阶非线性模型，考虑了可能施加在发电机上的外部干扰，假定干扰是有界的，基于输入-状态稳定性设计了一种鲁棒非线性控制律。理论分析和数值仿真表明所设计的控制律可以克服有界外部干扰的影响，使转子运行角、转子运行角速度、同步励磁发电机暂态电抗最终趋于稳态，验证了所设计控制律的有效性。