利用Stein-Weiss解析函数结合反向传播神经网络进行血管分割

吴明珠，陈瑛，李兴民

1.广州工程技术职业学院信息工程学院，广东广州510075；2.华南师范大学计算机学院，广东广州510631；3.南方医科大学珠江医院，广东广州510280

前言

1 BP神经网络

使用误差BP算法的BP神经网络，包括了两段学习过程［21］：（1）信号的正向传播，首先输入信号，然后通过隐含层作用于输出层的节点，经过非线性变换，产生输出层每个节点的实际输出值；（2）对输出误差进行BP，若前个过程得到的实际输出值与理想的输出值不相符合，则通过隐含层向输入层逐层反传，递归地计算出误差，根据此误差来循环调整权值，这也是神经网络学习训练的循环过程［22］。具体算法过程包括以下主要组成部分。

1.1 模式顺传播过程

将BP 神经网络定义为BPnet，样本输入向量Ak=(a1,a2,…,an)，输出向量Yk=(y1,y2,…yq)。在隐含层，输入向量Sk=(s1,s2,…sp)，输出向量Bk=(b1,b2,…bp)；在输出层，输入向量Lk=(l1,l2,…lq)，输出向量Ck=(c1,c2,…,cq)。其中，k= 1,2,…,m，为样本数，输入层设置的节点数为n，隐含层设置的节点数为p，输出层设置的节点数为q［22］。

从输入层到隐含层的权值设为wij，其中i=1,2,…,n;j= 1,2,…,p。从隐含层到输出层的权值设为vjt，其中j= 1,2,…,p;t= 1,2,…,q。隐含层阈值为θj，j= 1,2,…,p；输出层阈值为γt，t= 1,2…,q。

隐含层输出为：

输出层输入为：

输出层输出为：

作者用诗意的笔调，描述了她在虚拟的“海边草屋”，听到“竹林听雨”的诵读声，竟宿命般地被这位语言表达者磁性的声音吸引了，变得如醉如痴。从此，“竹林听雨”成为她寻寻觅觅的知音。作者对他们在虚拟空间的聊天，写得诗意隽永，禅味幽远，又恣意汪洋，显示两个人精神的标高。这样的聊天，是知的相遇，也应当是情的融合，爱的诉说，以至夜夜相见，不见不散。这一聊就是七年时光。

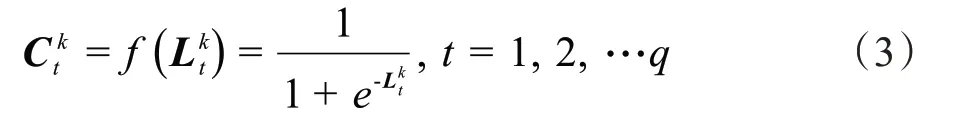
1.2 误差BP过程

把输出误差经过隐含层向输入层逐层进行BP，在这个过程中，误差沿梯度方向减小，并且对应于最小误差的权值和阈值在反复训练和学习后得以确定［23］。

输出层权值调整量为：

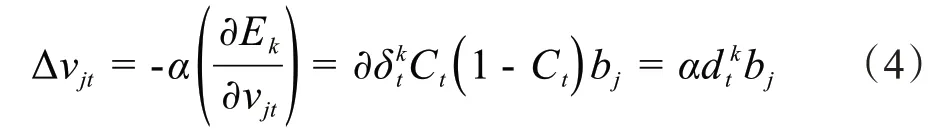
其中，α∈(0,1)，t= 1,2,…,q；j= 1,2,…,p。

输出层阈值调整量为：

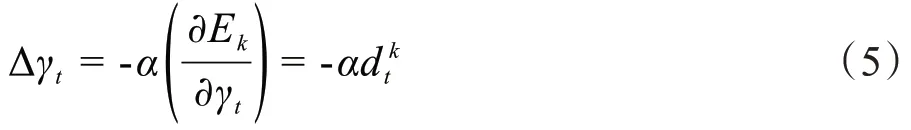
隐含层到输入层连接权值调整量为：

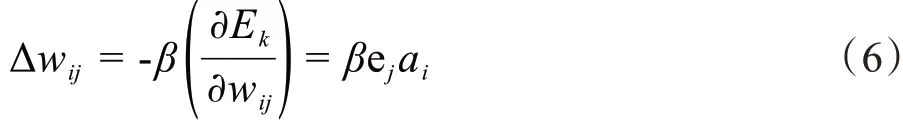
隐含层阈值调整量为：

每个节点的权值调整与每个学习样本的误差Ek成比例，这种思想即为标准误差BP 算法。但是如果把所有学习样本的全局误差全部输入到网络后再统一进行连接权值的调整，这种思想即为累积误差BP算法［23］，本研究使用的便是全局误差。

1.3 记忆训练

将一组样本输入网络后反复进行学习训练，通过调整网络参数即权值和阈值来控制实际输出值在规定的范围内。

1.4 学习收敛

网络的全局误差通过多次训练之后趋于最小值。在训练过程中，为避免收敛到局部最小点，本研究将一个小随机数即动量因子添加到每个权值上，并且适当改变隐含层单元的个数。

2 Stein-Weiss解析函数

Stein［24］在高维的Hardy空间中推广解析函数，引进了Stein-Weiss 解析函数的定义。设在Rn区域中的向量函数集F=(μ1,μ2,…,μn) ，若F是该区域上实调和函数的梯度，则称F是该区域的Stein-Weiss解析函数，也称为共轭调和函数系［21］。

F=(μ1,μ2,…,μn) 满足广义Cauchy-Riemann 方程：，特别当n=2 时，F=u+iv的解析充要条件是：(u,v)是Stein-Weiss解析函数［21］。

设：

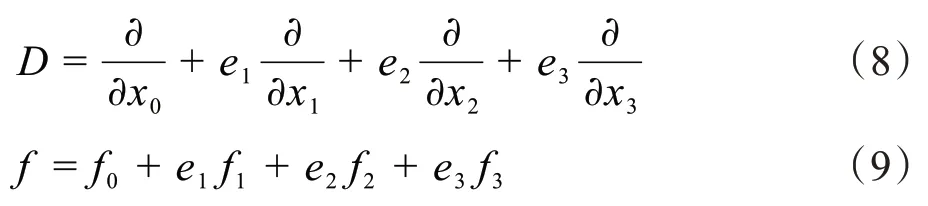
血管的生长恰好是多方向的，而Stein-Weiss 解析函数是高维函数理论，这为研究血管分割提供了适合的高维数学工具。与同为高维数学理论的八元数分析相比较，Stein-Weiss 相比八元数解析性更好。文献［21］中首次使用Stein-Weiss 解析函数特征进行血管分割，实验结果表明该方法分割出的血管更加精细。然而随着人工智能技术的发展，人工神经网络在医学图像分割技术领域也应用广泛，为了更好地提高自动诊断的准确度，本研究将Stein-Weiss 解析函数与神经网络技术相结合，提出一种新的血管分割算法。

3 基于Stein-Weiss解析性的BP神经网络算法

传统的BP神经网络血管分割算法由于对血管样本进行反复训练，网络学习收敛的速度较慢，所以花费时间较长；而且网络的训练程度也会影响识别效果，这也可能会导致识别率不高［25］。因此本研究提出了一种新的基于Stein-Weiss解析性的BP神经网络血管分割算法。因为在三维医学图像数据中血管的分布方向大多数是垂直的或者是倾斜的，所以本研究的算法综合考虑三维体素在斜方向和垂直方向的结构特征，即使用了体素的六邻域结构，然后将依据Stein-Weiss 函数解析性质所得到的特征值输入到BP神经网络的输入层进行反复训练，最终得到血管的分割结果。

3.1 定义体素的Stein-Weiss函数

定义六维向量空间中的向量函数f(x)，f(x)=f1e1+f2e2+f3e3+f4e4+f5e5+f6e6。其中f1、f2、f3、f4、f5、f6分别是体素点6个邻域的灰度值。向量函数的虚部e1、e2、e3、e4、e5、e6对应的数值是体素的上、下、左、右、前、后这6 邻域的坐标值［21］。体素的6 邻域如图1所示。

3.2 向量函数的差分式

将向量函数f(x)代入广义Cauchy-Riemann 式，得到差分形式，其中i≠j。

3.3 提取特征值

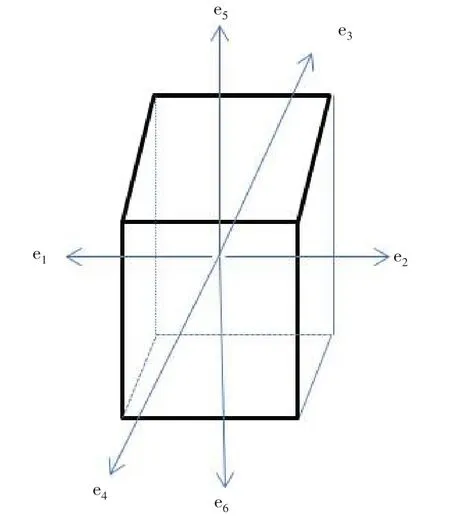
图1 体素的6邻域示意图Fig.1 Six neighborhoods of a voxel

实际图像的解析性不会都完全符合上面公式，根据Stein-Weiss 函数的解析性定理，使用恰当的阈值T来判断该体素点是否满足解析性。将步骤3.2中得到的公式改写成，并将它们展开得到如下16个特征值：

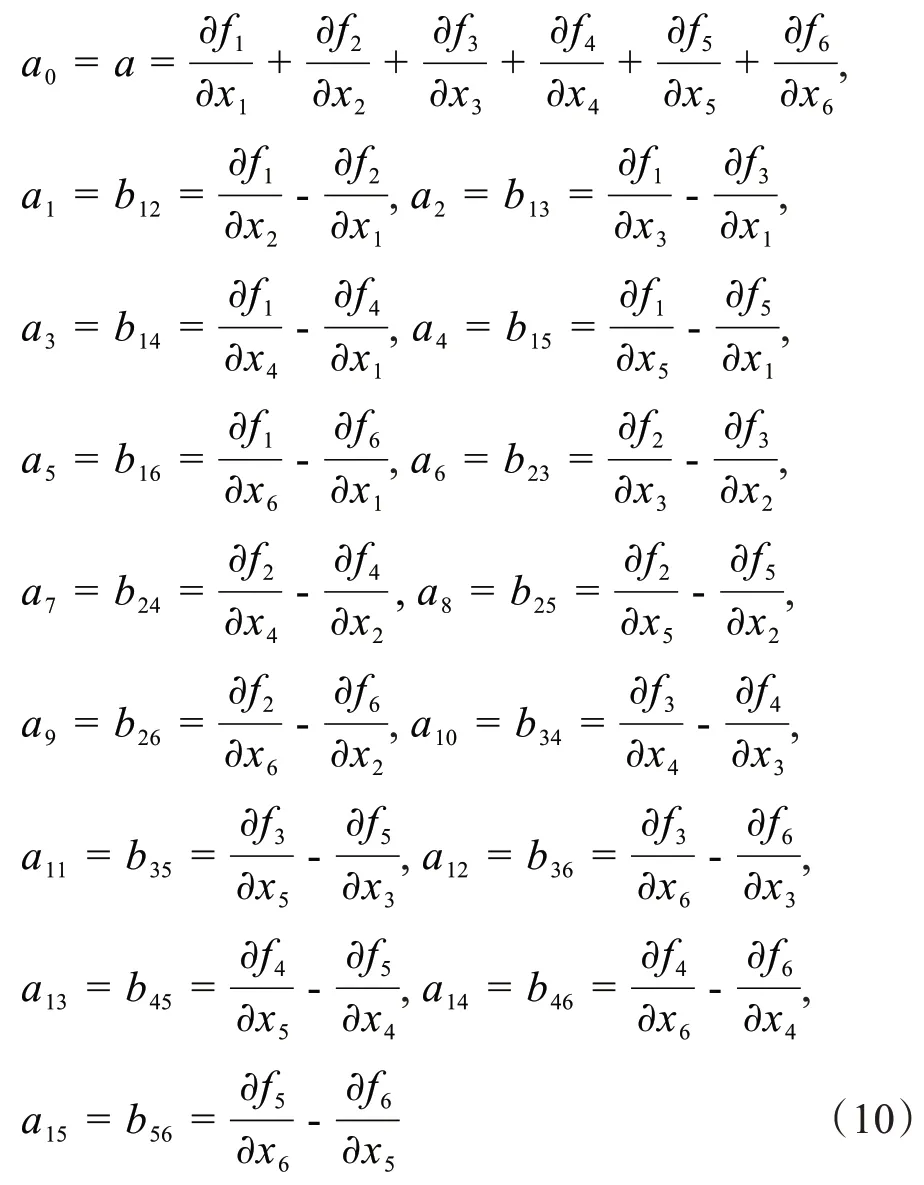
3.4 获取训练样本

设阈值T=0.6，若a0,a1,…,a15这16 个特征值均小于T，则认为该体素在血管内部，反之，则视该体素处于血管边缘。重复以上步骤。

3.5 记忆训练

将步骤3.4 即基于Stein-Weiss 解析函数的特性分割所得到的血管树作为BP 神经网络的样本，输入样本向量进行训练，直至误差达到设定阈值时停止，并保存权值和阈值。

3.6 学习收敛

选择待分割血管图像，提取该血管的特征值a0,a1,…,a15，以这16 个特征值输入到BP 网络的输入层，利用步骤3.5 已经训练好的网络对输入向量进行训练，动量因子设置为0.85，直到误差收敛到指定值0.001，最后输出的即为分割结果。本研究使用的BP神经网络的输入层有16节点，输出层有2个节点。合适的隐含层节点数的设置对网络的训练影响很大，故本研究根据文献［26］所提出来的确定方法进行实验测试，选取最佳节点个数为8。

4 实验结果与分析

本研究是在Window7 系统上做的实验；算法是使用Visual Studio 和MATLAB7.0 编程工具来实现；所有腹部CT 序列实验数据都是由南方医科大学珠江医院提供。选取肝静脉的造影数据S70 中的300张CT 切片进行实验，CT 数据大小为512×512×320。随机选取其中200 张CT 切片，将其作为文献［25］中的传统BP神经网络算法的输入样本；同时，分别利用文献［20］中提出的八元数和本研究提出的Stein-Weiss 解析函数的特性对这200 张CT 切片先进行分割并得到血管树边缘，然后将它们分别作为文献［20］提出的算法和本文算法中的BP 网络的输入样本。余下的100 张CT 切片图像作为网络测试样本，并将造影数据S70 中的第109 张CT 切片作为测试样本（图2）。

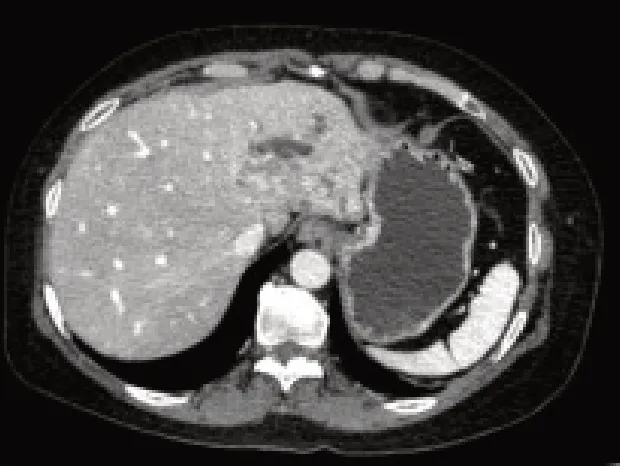
图2 S70第109张CT切片Fig.2 The 109th CT slice of S70

本研究对比了文献［20］中提出的基于八元数函数解析性质的BP神经网络分割算法以及文献［25］中的传统BP神经网络算法，分别对图2进行了血管分割，实验结果如图3所示。从这3个分割结果切片可以看出这3种算法都可以将大部分血管提取出来，然而相对于图3b和图3c，图3a能够分割出更多的血管分支。

图3 3种算法对S70的分割切片图Fig.3 Results of S70 segmentation by 3 algorithms

为了更直观地进行比较，分别对这3种算法的分割结果进行三维重建，得到的血管模型如图4所示。从这3 个三维重建结果比较可以看出图4a 利用本文算法分割出来的血管相对于图4b和图4c而言分割出来的分支要多，而且噪声点要少，所以本文算法分割效果更精细、更清晰。

为了客观评价本文算法的分割效果，使用医生手工分割结果作为分割评价的金标准［27］。对上述实验数据S70，分别运用本文算法、基于八元数解析性的BP 神经网络分割算法以及传统的BP 神经网络算法，计算出血管分割效果的敏感度和特异度，同时记录下3种算法各自所用的平均运行时间，最终测试结果如表1所示。

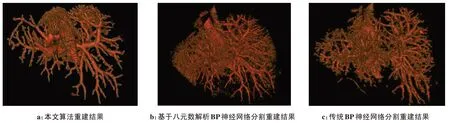
图4 3种算法对S70肝血管分割重建结果图Fig.4 Reconstruction results based on S70 hepatic vessel segmentation by 3 algorithms

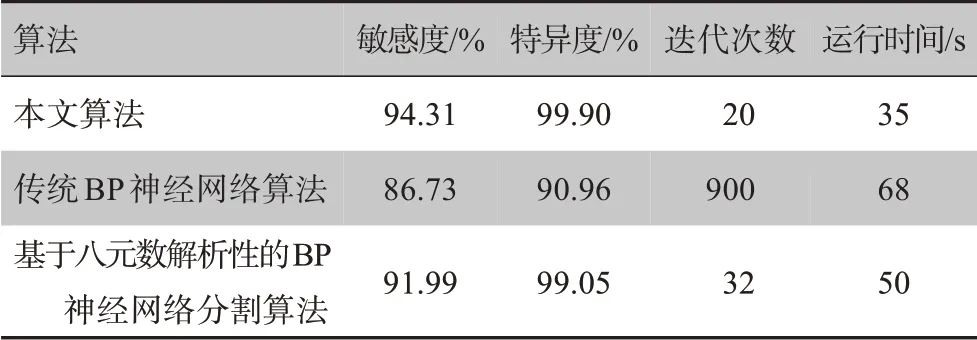
表1 3种算法的分割效果评价Tab.1 Evaluation of results of segmentation by 3 algorithms

从表1可以看出本研究所提出的基于Stein-Weiss 解析性的BP 神经网络血管分割算法对血管图像的分割有较好的实验效果。从实验结果的敏感度和特异度分析来看，相对于基于八元数解析性的BP神经网络血管分割算法和传统BP 神经网络算法，本文算法分割出的血管会更清晰、更精细。在运行时间方面，使用相同的机器配置，实验中选取200张S70数据图像作为样本进行训练，传统BP 神经网络需要训练迭代的次数较多，比较耗时，算法平均运行时间为68 s；基于八元数解析性的BP 神经网络分割算法虽然训练迭代的次数较少，但是前期进行八元数血管分割也需要耗费一些时间，所以该算法的平均运行时间为50 s；本研究所使用的血管分割算法，需要训练迭代的次数最少，然而同样需要前期进行Stein-Weiss 解析函数的血管分割，本文算法的平均运行时间为35 s，相对于前面两种算法而言，节省了时间。本研究所提出的基于Stein-Weiss解析性的BP神经网络血管分割算法具有较大的优势。

5 结语

本研究结合高维数学工具Stein-Weiss 解析函数与神经网络，提出一种基于Stein-Weiss 解析性的BP神经网络血管分割算法。和传统的BP神经网络算法比较，该算法提高了三维重建图像的精度，运算时间也达到了实时应用。不过从重建出来的三维血管树中可以看到一些噪声点，因此接下来的研究方向是：如何在保证分割精度和效率的前提下，提高分割的抗噪性。