基于BP神经网络沥青混凝土心墙堆石坝施工后期沉降预测

2020-07-10谭亮，王祥，喻成，李璐

水电与抽水蓄能 2020年3期

谭亮，王祥，喻成，李璐

（1.四川大学水力学与山区河流开发保护国家重点实验室，四川省成都市 610065；2.湖南省水利水电科学研究院，湖南省长沙市 410007；3.湖南省科宏大坝监测中心有限公司，湖南省长沙市 410007）

0 引言

自1949年葡萄牙建成第一座沥青混凝土心墙坝以来[1]，以沥青混凝土作为防渗心墙的土石坝迅速发展起来，近三十年来国内建造了众多的沥青混凝土心墙坝[2]。同大多数土石坝一样，沥青混凝土心墙堆石坝，存在检修困难，后期运行发现问题难以解决等问题，这就需要沥青混凝土心墙堆石坝在施工中提高质量标准。大坝沉降变形是评价大坝填筑质量和安全的重要参数之一，如果能够根据已有的监测资料，预测后面的变形趋势和变形量，对于指导大坝后续施工、运行和安全具有重要价值和意义。

针对沥青混凝土心墙堆石坝沉降预测，现有的预测方法主要有：理论方法、统计方法、神经网络法等。目前理论方法主要采用有限元计算，刘京茂等人[3]提出没有考虑碾压颗粒破碎的情况是目前有限元计算的高坝沉降变形比实测偏小的主要原因之一。肖亚子等人[4]通过三维有限元计算出坝体沉降为最大坝高的1.2%，结果明显偏大。故当前有限元计算结果与实际有较大差别，理论还尚不成熟表现为“低坝算大，高坝算小”；王彭煦等人[5]利用统计预报模型预测水布垭面板坝后期坝体最大沉降约为2.46m，竣工后还将继续沉降0.15m。但是统计方法的数学模型物理意义不明显，在一定程度上含有统计特性，它们建立在观测误差的数学期望全为零、各次观测独立以及观测误差呈正态分布的假定前提下，具有不确定性[6]；神经网络法具有自学习和处理非线性关系的能力，利用已观察到的数据，就可以通过训练找出隐含的非线性关系。现有文献的BP神经网络预测模型主要是针对面板堆石坝或者其他坝型[7]，其考虑的参数和情况不一样，模型大多数是建立在施工期、运行期或者更长时间内。本文通过某具体工程施工期后期原始观测资料，在数据总的测量时间和样本期数较少的情况下，建立普通BP神经网络预测模型后，改进模型，并对结果进行分析。

1 资料和方法

1.1 工程概况

某水库工程，是一项以灌溉为主、兼顾灌区乡镇工农业生活用水的水利水电工程。水库枢纽是该水库工程的渠首工程，总库容1512万m3，坝顶高程391.5m，最大坝高59.5m。属Ⅲ等中型工程，主要建筑物拦河坝、泄水建筑物、灌溉进水口等为3级建筑物。

挡水建筑物采用沥青混凝土心墙堆石坝，坝顶高程391.50m，坝顶宽度6.00m，坝轴线长度300.00m，最低建基面高程为332.00m，最大坝高59.5m。坝顶设“U”形防浪墙，墙顶高程392.70m。竖井溢洪道结合施工导流洞布置，由环形溢流堰、竖井及水垫塘、退水隧洞及下游消能工组成。

1.2 大坝沉降观测

大坝为沥青混凝土心墙堆渣坝属土石坝，根据规范要求建设沉降观测系统。为了观测大坝在施工期的沉降量，了解大坝填筑情况，为后续工程施工和初期蓄水做好准备。在2016年9月中旬，大坝填筑到高程391m附近时，建立了大坝临时沉降观测墩。测点布置如图1所示。

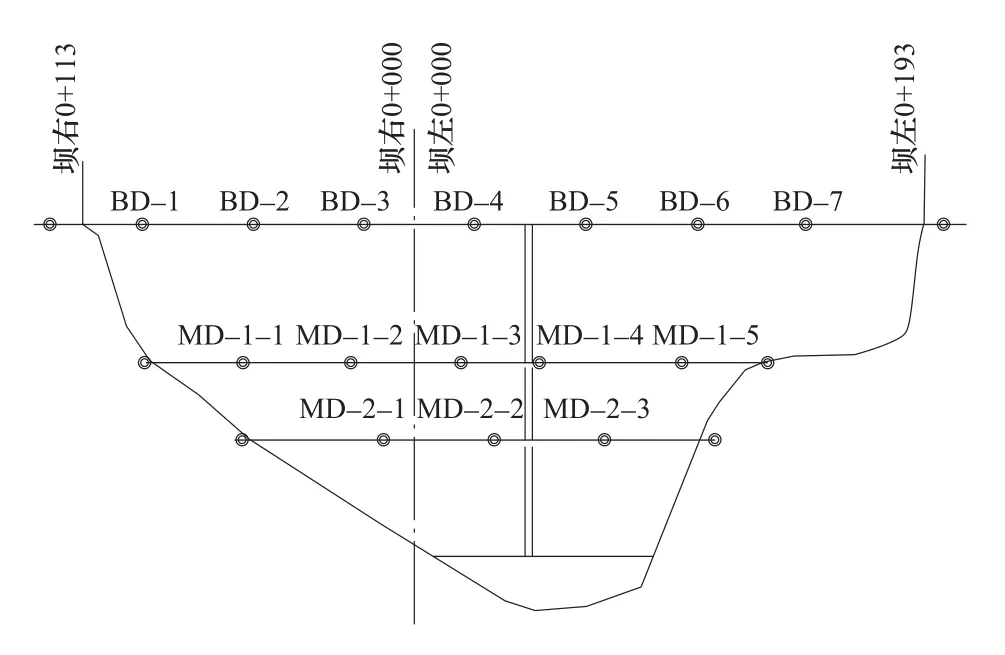
图1 临时观测墩布置图（下游立视图）Figure 1 Observation arrangement of temporary piers（Downstream vertical view）

1.3 沉降原因分析

沥青混凝土心墙堆石坝由两侧堆石体和中间沥青心墙组成的，对于大坝坝体沉降整体来看，影响坝体沉降的因素有很多，其中主要因素有坝体填筑材料、填筑质量、地基、水位、时效、外部温度、外力等，这些因素共同组成了一个复杂的非线性模型。该工程处于施工期，没有蓄水，没有水位因素的影响；堆石体经过碾压后的总体压缩量小；本次坝体填筑已到达坝顶，外力因素影响较小；堆石坝内部变形对温度不敏感，同时堆石体蠕变变形也可以归到时间因素，故主要考虑时效因素的影响[8，9]。

1.4 BP神经网络模型及原理

人工神经网络是由大量简单的基本元件——神经元相互连接，通过模拟人的大脑神经处理信的方式，进行信息并行处理和非线性转换的复杂网络系统[10]。人工神经网络具有强大的模式识别和数据拟合能力。

BP神经网络模型是人工神经网络模型的一种。BP网络是前向神经网络的核心部分，也是整个人工神经网络体系中的精华，广泛应用于分类识别、逼近、回归、压缩等领域。在实际应用中，大约80%的神经网络模型采取了BP网络或BP网络的变化形式[11]。本文利用的BP神经网络是包含多个隐含层的网络，具备处理线性不可分问题的能力。网络由输入层、中间隐含层、输出层构成，层与层之间全部连接，即上一层与下一层之间全部连接，同一层之间的神经元无连接。其结构如图2所示。

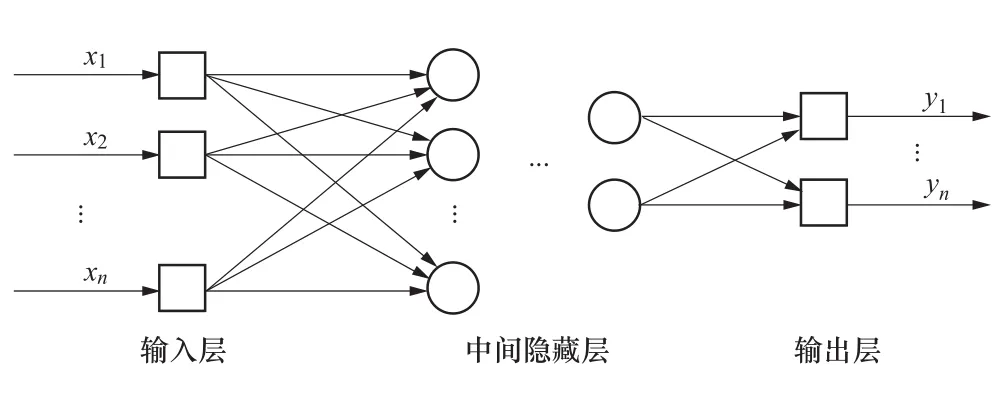
图2 神经网络结构Figure 2 Neural network structure

当一组学习样本提供给网络后，神经元的激活值从输入层经中间层向输出层传播。在输出层的各神经元获得网络的输入响应后，按减小期望输出与实际输出误差的方向，从输出层到中间层逐层修正各连接权值，最后回到输入层。随着这种误差信号反向传播修正的不断进行，网络根据误差从后向前逐层进行修正，网络输出层的正确率也不断上升，直到在允许的误差范围内[12]。具体如图2中x向量由输入层输入，经过中间隐藏层，最后由输出层输出得到y向量。因为误差反向传播过程中会对传递函数进行求导计算，这就要求BP神经网络的传递函数是可微的。常用的有Sigmoid函数、正切函数、线性函数等。本次采用Sigmoid函数，因为Sigmoid函数是光滑的，在分类时它比线性函数更精确，容错性较好；将输入从负无穷到正无穷的范围映射到0～1或-1～1区间内，具有非线性的放大功能。

BP神经网络学习方法属于最速下降法，即对于实值函数f（x），如果在某点x0处有定义且可微，则函数在该点处沿着梯度相反的方向-∇f（x0）下降最快。利用梯度下降法时，首先计算函数在某点处的梯度，再沿着梯度的反方向以一定的步长调整自变量的值。这其中工作信号正向传播、误差信号反向传播。利用BP网络对施工期的沉降数据资料进行输入和训练，从而预测一段时间后的沉降。

2 具体应用

通过对该水库沥青混凝土堆石坝施工期部分监测资料进行分析和BP神经网络建模，进行数据验证和后期预测。

2.1 数据选取

本次模型数据源选择坝顶临时观测墩建成后阶段时间内的序列数据，为保证原始数据的有效性，笔者选取了2016年9月至2017年4月坝顶部位变形测量数据，该段时间坝顶基本无施工作业。具体如表1所示。

表1 各测点沉降原始数据记录Table 1 Original records of settlement at various measuring points

根据表1选择沉降量最大的四个点BD-2 、BD-3、BD-4、BD-5进行分析，这四个点位于最大坝高附近，且总体沉降趋势基本符合大坝沉降规律。各测点累计沉降量过程线图如图3所示。

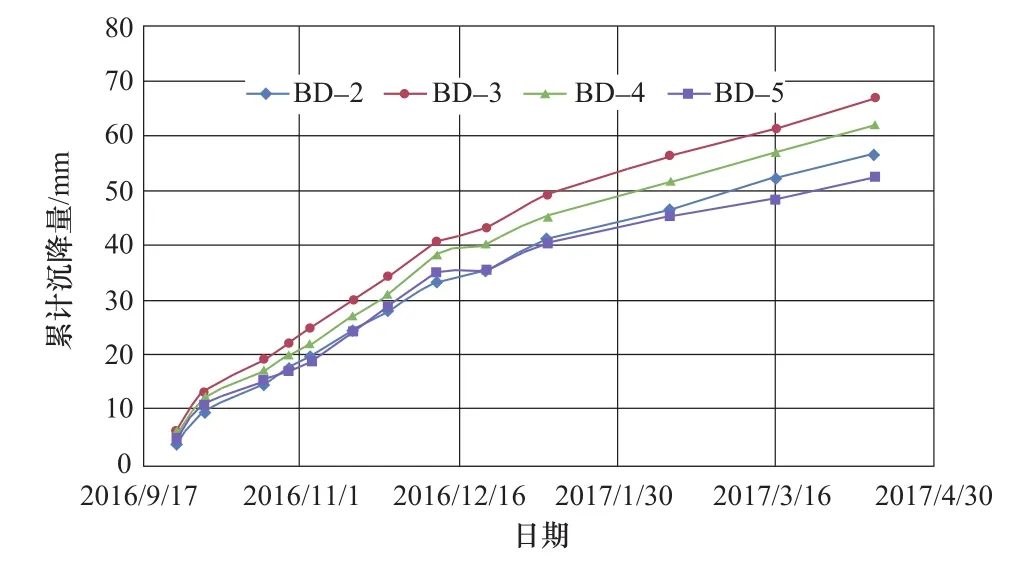
图3 各测点累计沉降量过程线Figure 3 Accumulative settlement process line of each measuring point

2.2 BP神经网络建立

MATLAB程序对于神经网络比较容易实现，程序编写简单，且有相应的函数和工具箱。本文采用MATLAB程序中的newff函数创建前向BP网络（net）。利用newff函数创建的BP网络调用格式为：

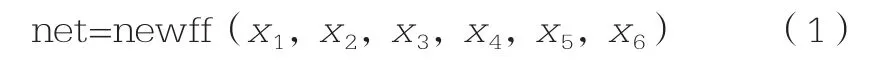
式中net表示创建一个神经网络；x1表示每组输入的元素的最大值和最小值；x2表示各层神经元的长度；x3表示各个层的传递函数；x4表示BP网络的训练函数；x5表示权值和阀值的BP学习算法，默认为“learngdm”；x6表示网络的性能函数。下面主要结合工程实际问题分析newff中前三个参数的设置。

本次利用BP神经网络主要是根据现有测量沉降数据预测和分析后期沉降量和趋势，从而为后续工程施工提供建议和参考。上文已经提到沥青混凝土心墙堆石坝工程施工期后期沉降量主要与时效有关，同时也是根据相隔时间输入，预测出相应时间的沉降量。故输入量中应该包含：已累计沉降量、已累计时间以及下一阶段的时间，输出向量为下一阶段相应沉降量。这样输入向量为三维，输出向量为一维。对于神经元结构，由于单隐层BP网络的非线性映射能力较强，本次采用单隐层的神经网络，即三层神经网络“输入层、中间一层隐含层、输出层”。对于中间神经元的个数，考虑经验公式网络的收敛速度，确定中间神经元个数为9个[13]。层与层之间采用sigmoid函数作为传递函数，第一、二层为“tansig”函数，输出在（-1，1）；第二、三层为“logsig”函数，输出在（0 ，1）内。故需将数据进行归一化处理。

查阅相关设计资料，设计中计算出该沥青混凝土心墙坝施工期沉降量为270mm；工程处于施工期后期，相应预测时间不宜太长，预测太长时间的沉降失去意义，综合考虑本次预测模型总天数为300天。进行归一化处理时，对沉降数据除以270mm；对时间数据除以300。以BD-3点为例，该点数据归一化处理如表2所示。同时施工期的沉降监测次数较少，为了提高BP神经网络预测模型的准确性，训练样本11组，检验样本2组，预测数据1组。

表2 BD-3数据归一化处理结果Table 2 Normalization processing of results of BD-3

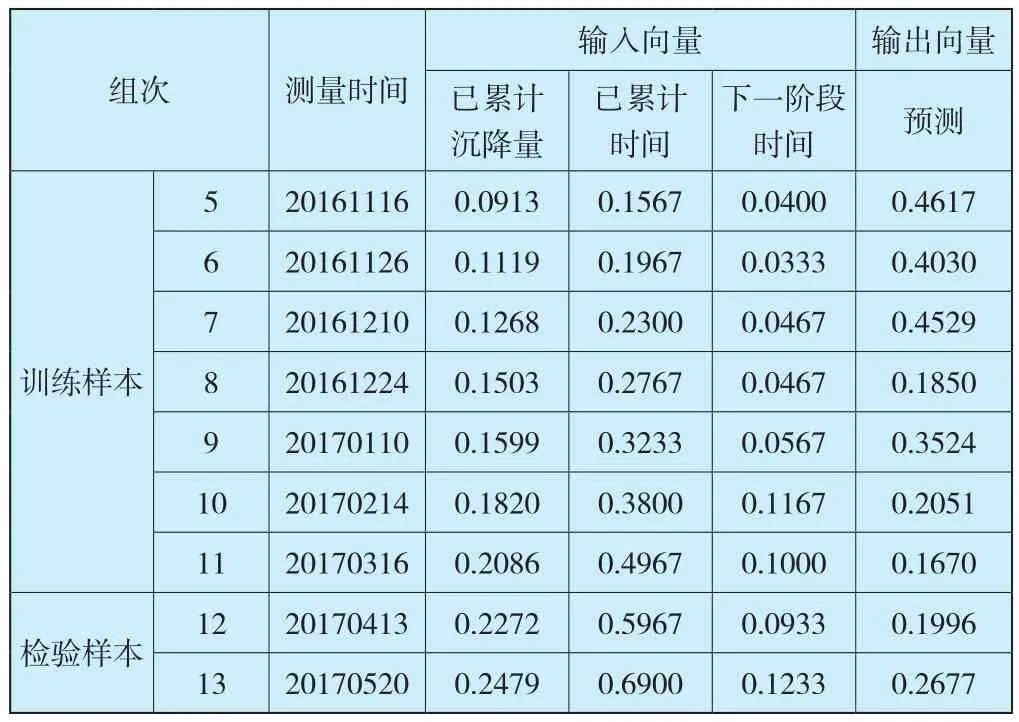
续表

因为神经网络的初始化的权值和阈值是随机的，BP神经网络每次结果不同，也正是因为每次的结果不一样，才有可能找到比较理想的结果。当数据量较少，在预测过程中很容易出现过拟合，预测结果也会不准确。为了找到合适的结果，在模型中考虑检验样本的误差和沉降量依次减小这一特性。具体来说就是利用MATLAB中的“while”循环结构来进行，每一次循环就相当于一次训练，将检验样本即12组和13组仿真结果与实测结果进行对比，进行误差计算，设置相应的误差项，同时在预测中考虑到实际的沉降量是逐月减少的。本次模型中将第12组误差设置为小于7%、第13组误差设置为小于11%，第14组预测沉降量小于第13组。将这些限定条件加入循环中，经过多次循环找到合适结果。以BD-3测点为例其训练过程如图4所示。

图4 训练过程和结果Figure 4 Training process and results

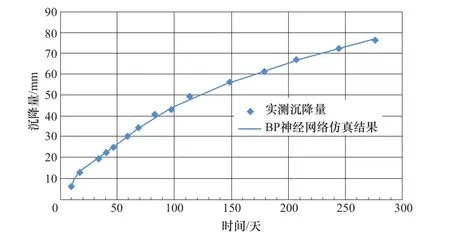
图5 实测沉降曲线与BP神经网络仿真结果对比图（BD-3）Figure 5 Comparisons between the measured settlement curve and the simulation result of BP neural network（BD-3）

2.3 计算结果

利用train函数对net进行训练，再用sim函数进行仿真，从而预测后期沉降。以BD-3测点为例其实测曲线与BP神经网络仿真结果如图5所示。各测点计算结果如表3所示。

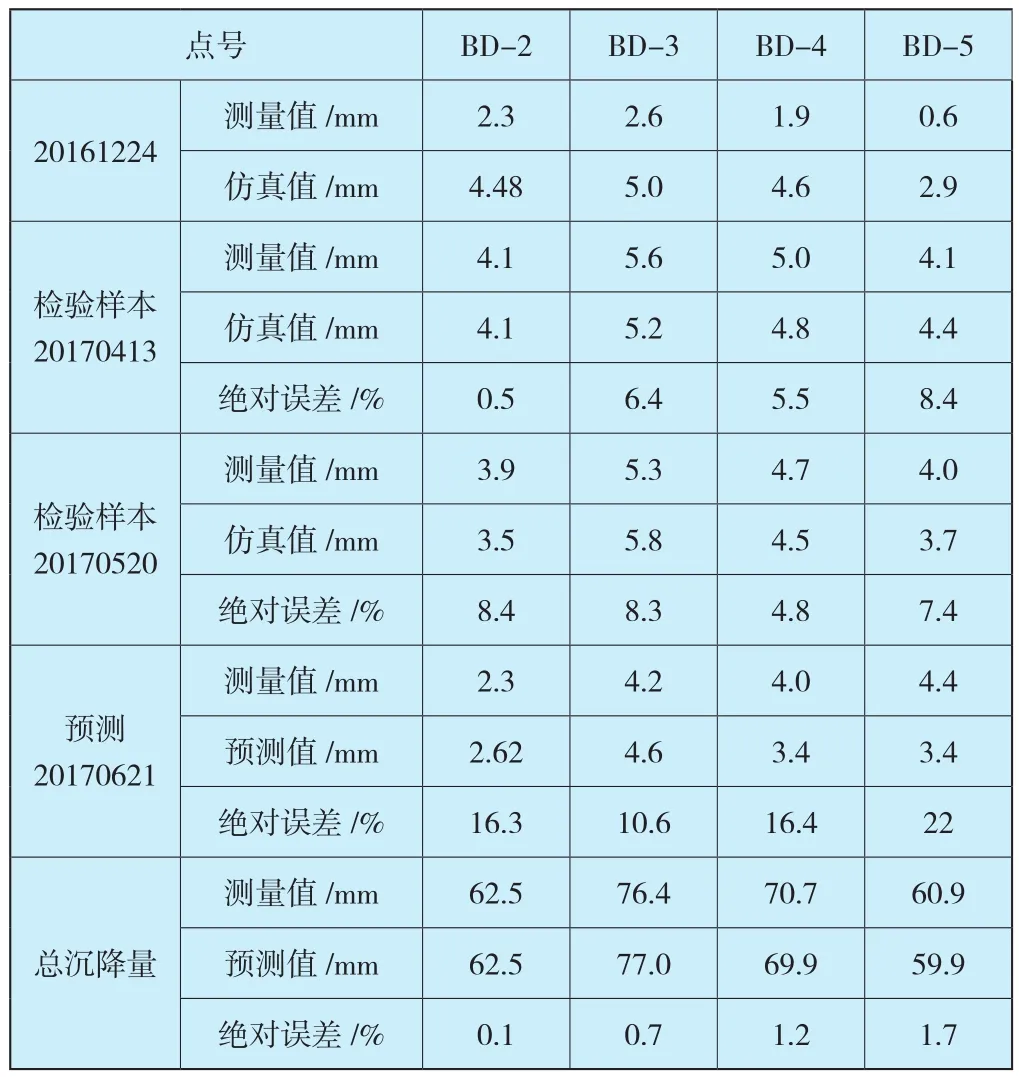
表3 各测点各时期预测值（BP方法）Table 3 Predicted value of each measuring point in each period（BP method）

为了对比BP神经网络模型预测结果的精度和合理性，本文也建立了统计回归模型对数据进行拟合，其结果如表4所示。

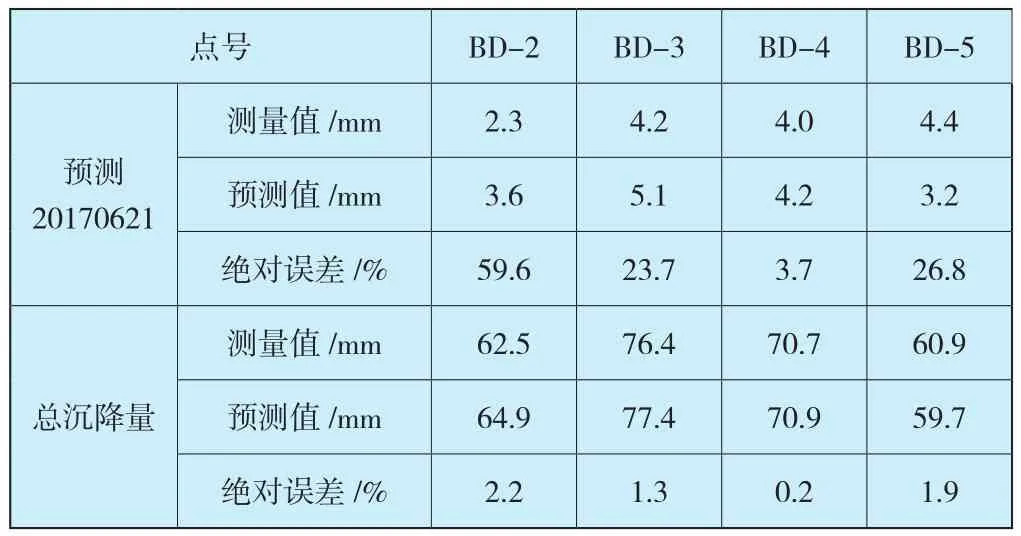
表4 各测点各时期预测值（统计回归方法）Table 4 Predicted value of each measuring point in each period（statistical regression method）

2.4 结果分析

根据表3各测点计算结果，两期检验数据中各测点绝对误差小于9%，预测数据各测点绝对误差小于22%，总沉降量误差小于2%。这是因为后期沉降量小，基数小，模型中输出为总沉降量，对总沉降量反应敏感。针对前文分析中第11期中由于测量误差导致数据整体偏小的问题，本次BP神经网络模型对其进行了仿真，通过对比第10期和第12期数据，其结果比较合理。对比表3和表4，BP神经网络模型预测精度明显高于统计回归模型。