基于二维DFT的多分量信号瞬时频率估计方法
2020-07-09谢好

摘 要:在进行多分量信号瞬时频率估计时,存在较大误差,为此提出基于二维DFT的多分量信号瞬时频率估计方法。首先通过建立多分量信号模型获取到多分量信号瞬时频率的相参特性,然后利用二维DFT技术对多分量信号脉冲特性进行变换,最后利用加权均值的方法求出多分量信号瞬时频率,以此完成基于二维DFT的多分量信号瞬时频率估计。经实验证明,设计方法估计误差小于传统方法。
关键词:二维DFT;多分量信号;瞬时频率;估计
中图分类号:TN911.72 文献标识码:A 文章编号:2096-4706(2020)23-0058-03
Instantaneous Frequency Estimation Method of Multicomponent Signals Based on Two-Dimensional DFT
XIE Hao
(Henan University,Kaifeng 475004,China)
Abstract:There is a big deviation in the instantaneous frequency estimation of multicomponent signals,so a method of instantaneous frequency estimation of multicomponent signals based on two-dimensional DFT is proposed. Firstly,the coherent characteristics of the instantaneous frequency of the multicomponent signal are obtained by establishing the multicomponent signal model. Then,the pulse characteristics of the multicomponent signal are transformed by using the two-dimensional DFT technology. Finally,the instantaneous frequency of the multicomponent signal is obtained by using the weighted average method,so as to complete the instantaneous frequency estimation of the multicomponent signal based on the two-dimensional DFT. The experimental results show that the estimation error of the design method is smaller than that of the traditional method.
Keywords:two-dimensional DFT;multicomponent signal;instantaneous frequency;estimation
0 引 言
瞬时频率是电子信号处理中最常用的一个术语,传统的瞬时频率概念是指电子信号傅立叶参数瞬时发生的变化,从根本上是指电子信号在某一瞬间的总体表征。电子信号瞬时频率物理意义就是指电子信号在单位时间内运动的次数,可以反映电子信号在单位时间的频率变化趋势[1]。在实际应用中,通常是非平稳的、多分量信号,对其进行瞬时频率估计,以达到非平稳电子信号处理的目的,更便于在语音、雷达、声呐等领域中应用,在目标探测、信号定位、信号跟踪以及信号识别中都起着不可代替的作用。
由于多分量信号瞬时频率估计是对多个分量信号频率同时进行瞬间估计,并且多分量信号的参数特征不够明顯,因此多分量信号瞬时频率估计具有较高的难度,若要实现对多分量信号瞬时频率估计,需要对获取到的瞬时频率进行大量的处理,通过处理工作得到多分量信号的参数特征。当前,多分量信号瞬时频率估计的方法主要有相位差分法、相位建模法以及时频分步法三种方法。其中,相位分差法是用离散时间域的差分运算,该种估计方法在应用中计算比较简单,但是对多分量信号的噪声比较敏感,容易受到多分量信号的噪声干扰从而影响到估计精度[2];相位建模法是将多分量信号瞬时频率的估计转化为多项式相位的阶次以及其系数的估计,这种方法虽然在估计精度上优于相位分差法,但是这种估计方法对于一些具有非线性相位的非平稳多分量信号的瞬时频率估计仍旧具有较大的误差,因此该方法也存在一定的缺陷[3];时频分步法是通过Cohen、分布等时频分布估计信号的瞬时频率,这种方法虽然具有较好的抗噪声能力,多分量信号噪声对估计算法的运算影响较小,但是其计算量比较大,在运算过程中一旦出现差错,还是会降低多分量信号瞬时频率估计精度[4,5]。
因此通过以上对目前多分量信号瞬时频率估计现状的分析,发现存在的主要问题为估计方法存在较大误差,无法满足多分量信息瞬时频率估计需求,为解决上述问题,本文提出利用二维DFT进行多分量信号瞬时频率估计的方法。
1 基于二维DFT的多分量信号瞬时频率估计方法设计
1.1 建立多分量信号模型
对于多分量信号瞬时频率估计,首先需要建立相应的多分量信号模型,利用该模型获取到多分量信号瞬时频率的相参特性,为后续多分量信号瞬时频率估计提供数据依据,建立多分量信号模型。
假设多分量信号脉冲重复间隔是一个已知参数,已经精确已知,经过反复多次采集多分量信号后,采样频率与多分量信号脉冲重复频率成倍数关系,则多分量信号模型用公式表示为:
x(n)=∑LKP (1)
式(1)中,x(n)为多分量信号模型;L为一个多分量信号脉冲重复间隔内的多分量信号采样点数;K为多分量信号脉冲数量;P为单个多分量信号脉冲的波形频率;f为下变频后残余的载频;μ为多分量信号下变频后残余载频的初始相位;ρ为多分量信号的循环对称复高斯噪声。利用以上建立的多分量信号数学模型获取到多分量信号瞬时频率的相参特性,该相参特性可以通过多分量信号的脉冲波形表示,由于多分量信号的脉冲波形的能量都集中在信号的脉冲内部,其在多分量信号模型中用公式表示为:
P(n)=0 n≤0,n≥m (2)
式(2)中,m为多分量信号的脉冲波形采样点数。利用式(2)获取到多分量信号模型中多分量信号相参特性,用于后续多分量信号瞬时频率估计。
1.2 设计基于二维DFT的多分量信号瞬时频率估计算法
建立完多分量信号模型后,本文设计了一个与该模型配套的多分量信号瞬时频率估算法。在多分量信号模型中,将多分量信号脉冲利用二维DFT变换为二维单音多分量信号,再对变换后的信号加权均值估计多分量信号瞬时频率,具体的计算过程为如下文所述。
首先将多分量信号模型中的所有信号按照脉冲重复间隔进行重新排列,并仅保留多分量信号的脉冲部分,因此可以得到一个多分量信号脉冲集合y[6]。将得到的多分量信号脉冲集合中信号脉冲的慢时间维度和快时间维度分别扩零,利用二维DFT技术对其进行二维DFT变换处理,其变换公式表示为:
y=∑(M-M1)(K-K1) (3)
式(3)中,M为快时间维度扩零后,多分量信号二维DFT变换前的脉冲波形长度;M1为快时间维度扩零后多分量信号二维DFT变换后的脉冲波形长度;K为慢时间维度扩零后,多分量信号二维DFT变换前的脉冲波形长度;K1为慢时间维度扩零后,多分量信号二维DFT变换后的脉冲波形长度。多分量信号在慢时间维度和快时间维度中可以看作为一个单音多分量信号,其二维DFT变换在慢时间频率维度为sinc函数,并且呈现单峰特性,无法使用峰值搜索法,因此文本选用加权均值的方法对变换后的多分量信号频率进行估算,其计算步骤为:
第一步:利用二维DFT变换后的脉冲频率绘制出多分量信号频谱曲线,通过二维搜索计算出多分量信号频谱的峰值点。第二步:在多分量信号脉冲慢时间频率维度处设定门限判别,计算出多分量信号脉冲快时间维度频谱分布范围。第三步:假设F为多分量信号频谱上第一个高于门限值的瞬时频率点,V为多分量信号频谱上最后一个高于门限值的瞬时频率点[7]。使用F到V范围内的瞬时频谱点,通过功率加权平均法计算出不同时间维度频率中心,在计算过程中需要充分利用多分量信号慢时间与快时间维度的能量值。第四步:通过二维DFT变换的采样点数,经过换算得到不同时间维度下多分量信号的瞬时频率,计算公式为:
(4)
式(4)中,f为多分量信号瞬时频率估计值;fs为多分量信号频率对应的瞬时时刻。利用上述公式计算出多分量信号瞬时频率估计值,以此完成基于二维DFT的多分量信号瞬时频率估计,流程图如图1所示。
2 实验论证分析
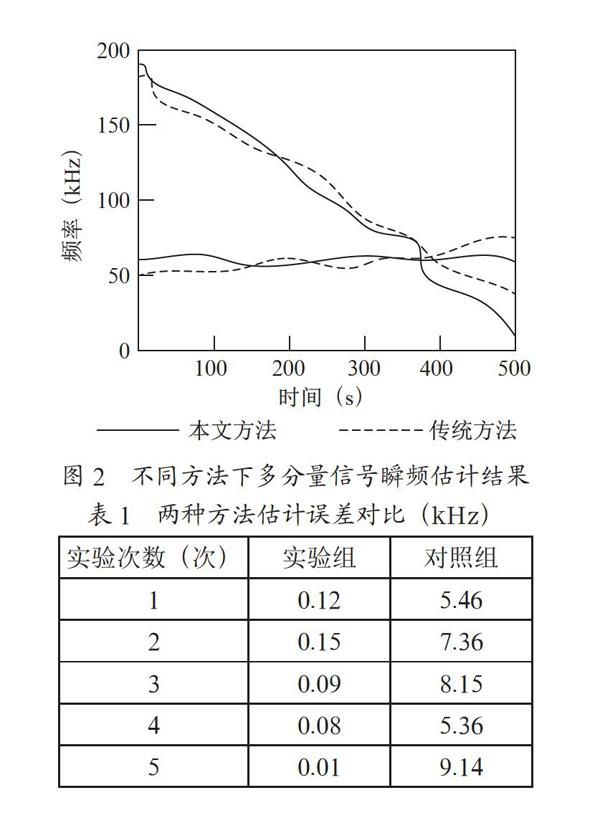
实验以某实测雷达多分量信号作为实验对象,在MATLAB平台上进行仿真,该信道多分量信号带宽为2.5 MHz,多分量信号脉冲串宽度为2.5 μm,多分量信号脉冲重复间隔为45 μs,多分量信号脉冲数量为156,多分量信号采样频率为65 MHz。利用此次设计方法与传统方法对该信道多分量信号瞬时频率进行估计,实验将设计方法设定为实验组,将传统方法设定为对照组,设计对比实验,统计两种方法的估计误差,实验次数为30 000次。实验按照该信号多分量信号特征建立数据模型,为了更好地验证基于二维DFT的多分量信号瞬时频率估计方法的有效性,在多分量信号中模拟了多种干扰,其中包括缓变干扰、10 dB噪声、50 dB噪声干扰等,干扰的频率在0.26~2.65 MHz范围内,瞬频估计结果如图2所示。
实验通过数据记录仪对两种估计方法估计结果进行记录,并使用SPSS软件对两种方法估计值与实际值对比,计算出两种方法的估计误差,实验随机抽取30 000次实验次数中的5次估计结果误差作为实验结果,对两种多分量信号瞬时频率估计方法进行对比分析,实验结果如表1所示。
从表1中可以看出,设计方法估计误差远远小于传统方法,最小误差值仅为0.01 kHz,而传统方法最大误差已经达到9.14 kHz,因此實验证明了基于二维DFT的多分量信号瞬时频率估计方法在精度方面优于传统方法。
3 结 论
本文在传统方法的基础上,结合二维DFT技术,提出了一套新的多分量信号瞬时频率估计方法,解决了多分量信号瞬时频率估计存在误差的问题,同时也解决了多分量信号瞬时频率估计问题,对多分量信号瞬时频率估计具有良好的借鉴意义。由于此次研究时间有限,提出的基于二维DFT的多分量信号瞬时频率估计方法可能还存在一些不足之处,同时该方法在实际应用中运算量比较大,并且估计精度和效率还有待进一步提高,因此今后还需要对基于二维DFT的多分量信号瞬时频率估计方法进行更深一步的研究,对其进行不断改进和创新,以提高多分量信号瞬时频率估计效率和精度。
参考文献:
[1] 曹伟浩,姚直象,夏文杰,等.基于插值短时分数阶傅里叶变换-变权拟合的线性调频信号参数估计 [J].兵工学报,2020,41(1):86-94.
[2] 康德,马增强,李响,等.基于Steger算子的非平稳信号瞬时频率估计方法 [J].济南大学学报(自然科学版),2020,34(4):335-341+349.
[3] 胡瑾贤,高墨昀,王金锋.外场条件下辐射源脉内瞬时频率特征提取与个体识别有效性分析 [J].舰船电子对抗,2020,43(2):70-74.
[4] 王增科,赵加祥,徐微,等.一种低信噪比条件下的瞬时频率估计算法 [J].东南大学学报(自然科学版),2020,50(4):684-688.
[5] 生雪莉,穆梦飞,殷敬伟,等.基于稀疏分解的水下运动目标多普勒频移估计方法[J].哈尔滨工程大学学报,2020,41(10):1429-1435.
[6] 赵红梅,崔艳.一种基于新误差标准的ANF线性调频信号参数估计方法 [J].山西师范大学学报(自然科学版),2019,33(1):66-72.
[7] 翟华,茆弘民,左根明,等.融合KFCM及频谱质心的瞬时频率估计算法研究 [J].电子测量与仪器学报,2019,33(7):1-10.
作者简介:谢好(2001.01—),女,汉族,山东菏泽人,本科在读,研究方向:电子信息科学与技术。
