我国上市银行股票超额收益率影响因素的实证分析

任颖

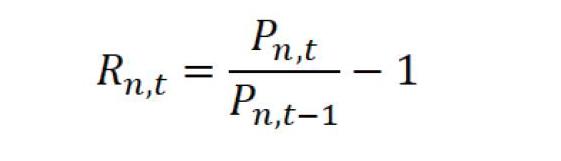
摘 要：本文主要利用CAPM模型对我国A股市场上的金融机构进行实证检验，选取了16家上市银行的股票数据进行实证分析。结果表明，CAPM模型并不是完全失效，市场的风险溢价对于股票收益有着显著的解释能力，但同时还发现，模型拟合并不是很好，说明存在遗漏的变量，并以此对模型进行了修正，加入了规模因子和账面市值比因子。修正后的模型比原有的单因素CAPM模型来说，拟合程度有所提高，说明在我国银行业确实存在着规模效应和账面市值比效应影响着股票的超额收益率。

关键词：CAPM模型  三因素CAPM模型  贝塔系数

中图分类号：F832.39 文献标识码：A 文章编号：2096-0298（2020）01（a）--03

1 研究背景及意义

资本资产定价模型（Capital Asset Pricing Model）在金融理论领域有着卓越的贡献，特别是在为个人资产的期望收益率与风险定价方面有着重要的地位，并且CAPM模型在资产价格和预期收入之间进行比较提供了可能性，并以此来确定该资产的风险。CAPM模型假设认为的线性关系体现在证券的期望收益率与整个大环境的市场风险中，并且可以使投资者在股票或证券的收益与风险中进行权衡。

对于传统的资本资产定价模型来说，其苛刻的条件是判断一个市场是否成熟的标志，根据CAPM模型理论，以及改进的三因素CAPM模型，市场风险组合的超额收益率、规模因子、账面市值比因子能解释影响银行股票超额收益率的问题，并适用于西方资本市场。因借鉴西方投资理论的模型来研究股票收益率影响因素对于研究中国股票市场，尤其对金融体系中银行这整个行业的市场中超额收益率的影响因素，以及该行业是否稳定的发展具有现实的重要意义。

2 数据选择

本文的样本数据来自Resset数据库（锐思数据库），选取了最近三年，即2014年10月31日到2017年10月31日跨度为三年的16家上市银行股票的周度数据。选择该阶段数据出于以下几点原因：2014年到2017年经历了股票市场上的熊市以及牛市。在中国股票市场连续五年低迷后，在2014年首先迎来了小盘股的牛市，紧接着便是整个股票市场的繁荣。截至2017年中国股票市场震荡，经历了由高到低的下滑趋势，市场表现全面，排除政策影响。这段时间股票样本规模各异，呈现出多样性，区间跨度大，样本量充分有利于研究。银行股票作为我国金融行业股票的重要组成部分，其数量占整个金融股票数量的50%，总市值占整个金融行业的30%以上，因此选择银行股票进行研究具有重要意义。

3 数据前期处理及分组

样本数据剔除了数据缺损的银行股票数据，首先对16家股票进行分组处理，根据t（t=2014，2015，2016）年末的总市值和账面市值比由大到小进行分组。根据账面价值的大小可分为两组，B组和S组，每组八只股票一共三年总计6组。然后根据账面市值比（BE/ME）的高低进行排序，得到H组和L组，L组代表账面市值比较低的低价值组，H组代表账面市值比较高的高价值组，同样每组八只股票，总计6组。于是两两交叉得到四个组，如表1所示。

4 相关计算

4.1 周收益率计算

周收益率为考虑到现金股利再投资的周资本收益率：

其中，表示股票n在t时刻的周资本收益率，表示股票n在t时刻的收盘价，表示股票n在t-1时刻的开盘价。

市场收益率采取上证指数作为市场收益率。

无风险收益率采用的是银行一年的定期存款利率，用复利的方法计算出周度无风险收益率。

4.2 总市值计算

本文中的市值（ME）采用的是股票的总市值，计算方法为：

其中，表示该股票的总股数，表示股票n在t时刻的收盘价。

4.3 账面市值比计算

账面市值比（BE/ME）指股票n在t时刻的股东权益除以该股票的市值，股东权益的计算可以由每股净资产乘以总股数得出。

4.4 组合周收益率计算

在进行组合周收益率时利用的计算方法如下：以小規模低账面市值比为例，首先在Excel表格中筛选出2014年S/L组的四只股票分别为：000001、002142、601009、601998、601939。然后将每只股票在2014年各个周的总市值进行加总。

其中，表示小组总市值，表示各个小组中的个股市值。

分别得到每只股票在2014年的周个股总市值，因此可以得到S/L整个组在2014年的周小组总市值，计算各个股票的权重，利用各个股票的权重和周收益率相乘可以得到整个小组的加权平均周收益率，2015年、2016年与2014年算法相同。S/H、B/L、B/H各个小组三年的周平均收益率的算法与之前相同。

其中，表示小组中的个股总市值占组合总市值的权重。

其中，表示组合收益率，表示个股周收益率。

5 实证检验

在对构建的模型进行回归前，利用STATA软件对市场收益率，以及进行分组处理后的四个组合的周收益率进行ADF检验，检验的目的就是观测该时间序列数据是否存在单位根并出现伪回归的现象。

利用STATA软件平稳性检验结果表明，四个组合P-value都为0，故拒绝原假设，接受各个组合以及市场收益率不存在单位根的假设，时间序列数据平稳。回归模型为：

其中， rit-rft表示组合i在t时刻的风险溢价，表示市场组合的风险溢价，为随机干扰项。

结果分析如表2所示。

从表2中可以看到四个组的解释变量的系数都为正，说明市场组合的风险与组合的收益率成正相关，说明风险越大收益率越高。

从表2各个组合的β系数可以看到，四个组合的β系数都小于1，说明组合的收益率对于系统风险的变化的敏感程度较小。但S/L组合的β系数为0.9336069，相对较高，S/H组的β系数也相对较高，说明小规模低账面市值比的组合的风险溢价相比于其他三个组合来说要高于市场的风险溢价，这与之前所做的描述性统计相一致，投资小规模组的系统性风险较大，因此获得的风险补偿也较多。

异方差检验：检验异方差的方法采用white检验法。

由检验结果可以发现SL组合以及BL组合的P值小于5%的显著性水平，因此拒绝原假设，认为SL和BL组存在异方差，而SH和BH组不存在异方差。

自相关检验：对于自相关检验采用的是BG检验。

四个组合的P值明显大于0.05，认为四个组合不存在序列自相关的现象。

6 模型修正

根据Fama-French的三因素CAPM模型，首先构造规模因子和账面市值比因子：

修正后回归模型。

加入规模因子和账面市值比因子的CAPM模型如下：

rit-rft表示组合i在t时刻的风险溢价，表示市场组合的风险溢价，为规模因子，为账面市值比因子，为随机干扰项。

回归结果分析如表3所示。

从表3中可以看出，同修正前的模型一样，贝塔系数为正且四个组合的P值都显著，说明市场组合的超额收益率对于组合的收益率影响显著且对组合收益率有正向影响。

修正后的模型多加了两个影响因子，对于规模因子来说，四个组合的P值在5%的显著性水平下显著，说明股票的规模大小会对股票的收益率有显著的影响。两个小规模组（SL，SH）的规模因子的系数较大，分别为0.544与0.642，说明对于投资小盘股票来说，投资风险要高，对于风险的补偿要大，规模效应更明显。对于两个大规模组合（BL，BH）来说，规模因子的系数为负，说明规模对收益率有着负向的影响。

进行异方差检验，通过white检验的结果可以发现，四个组合的P值在5%的显著性水平下并不显著，接受不存在异方差的假设。

对回归结果再进行多重共线性检验，通过VIF值可以看到，四个组合的VIF值都明显小于10，因此不存在多重共线性。

7 结语

通过对我国金融行业中16只股票进行CAPM模型分析可以看出，我国银行股票的组合的风险溢价或是超额回报率与市场风险的超额回报率成正相关，投资银行股票的风险相比于其他股票来说相对较低，整个行业的β系数都小于1，说明银行这个行业的收益率的变动情况对市场的变动敏感程度较低，抗风险能力较强，在市场有较大波动时收益率情况较为稳定。但这也说明在市场处于牛市的状态下银行股票的收益率较差。

虽然根据分析结果显示，银行股票的超额收益率与市场的超额收益率相关，符合CAPM模型，并在实证中通过检验，但从拟合优度来看，拟合结果并不是太高。由于以下原因会导致拟合效果较差：模型本身的局限性，CAPM模型要求服从有效市场假说，假说对于现实中的股票市场来说条件过于苛刻，特别是在中国这个新兴的股票市场。中国股票市场相比于西方发达国家的股票市场成熟较晚，发展速度快，由于股票市场内幕交易严重，信息的透明程度还不够高，因此导致中國整个股票市场不能满足有效市场假说。对于金融股票中的银行这个特殊的行业来说，基于它在国民经济中的重要地位，政策对于其影响也会导致股票的收益率不能完全用市场的超额收益率来进行解释，模型中还存在一些遗漏的变量。

在对模型进行修正之后发现，影响股票超额收益率的因素除了市场超额收益率之外，还有规模因素和账面市值比因素，在通过对模型进行回归后发现拟合系数明显提高，说明加入两个因子之后提高的回归拟合程度的显著性，说明在银行这个行业中确实存在着规模因素和账面市值比因素对于整个行业股票收益率的影响。

参考文献

邹舟，楼百均.CAPM模型在上海股票市场的有效性检验[J].企业经济，2013，32（01）.

赵清，乌东峰.CAPM资产定价机制及中国适用性研究[J].东南学术，2015（06）.

薛华，周宏.上海证券市场CAPM的实证检验[J].财经问题研究，2001（11）.

靳云汇，刘霖.中国股票市场CAPM的实证研究[J].金融研究，2001（07）.

勾东宁，王维佳.CAPM模型的实证检验——基于我国上市银行股2011—2014年的数据分析[J].管理世界，2016（03）.

李红霞，邸鸿喜，李琰，等.CAPM模型在中国股票市场中的有效性检验[J].统计与决策，2014（14）.