温度和桥面不平顺对下承式系杆拱桥车桥振动的影响

王杨兵

摘 要：为研究桥面平顺程度与车桥动力效应的关系，利用了有限元法和动力平衡原理，建立下承式系杆拱桥的车桥耦合系统模型，分析在车辆荷载作用下，考虑温度场下桥面的变形与桥面不平顺度对结构动力响应的影响，得到其桥梁关键部位的振动响应。结果表明动力响应随桥面不平顺等级的增加而增加，温度变形对车桥耦合影响偏于不利。

关键词：下承式系杆拱桥;动力响应;不平顺;温度变形;有限元

Abstract：In order to study the influence of bridge deck smoothness on vehicle-bridge dynamic effects，the finite element method and the principle of dynamic balance were used to establish the vehicle-bridge coupling system model of the through-tied arch bridge.The influence of the deformation of the surface and the unevenness of the bridge deck on the dynamic response of the structure gives the vibration response of the key parts of the bridge.The results show that the dynamic response increases with the increase of the unevenness of the bridge deck，and the temperature deformation is unfavorable for the effect of vehicle-bridge coupling.

Keywords：Through-type tied arch bridge，Dynamic response.Not smooth，Temperature deformation，Finite element

高速运动的车辆对桥梁的冲击作用直接影响着桥梁的工作状态，同时桥梁的振动也影响着车辆运行的舒适性和安全性[1]。近年桥梁建设快速发展，使用的轻型高强材料的系杆拱桥越来越多，桥面板厚度趋于减小，加之日常交通量的增加，使得车桥耦合效应更为显著，正确分析大跨度系杆拱桥在车辆荷载作用下的动力冲击效应很有必要[2]。

考虑车桥耦合振动，分析汽车对桥梁的冲击效应需要求解桥梁结构在车辆荷载作用下的动力响应，当前已有许多学者对此进行了研究。陈代海等对车桥耦合振动分析方法的整体法和分离法进行了对比研究[3]。Ding等研究了车桥耦合振动对桥梁伸缩缝的冲击作用，指出了伸缩缝构造、车辆荷载及桥梁内力等因素对冲击作用的影响[4]。Kim等建立了分析车桥耦合振动的三维模型，举例计算了一个钢梁桥在车辆荷载下的动力响应[5]。上述研究在不同方面得出了一些有价值的结论。但是车桥系统的耦合振动问题与许多因素有关，有些还未被考虑。如今大型有限元软件的广泛使用大大提高了结构的计算速度，使得研究更多因素对桥梁结构的车桥耦合振动及其动力响应分析成为可能。

车桥间的相互作用力与接触面的不平顺度相关，桥上路面的不平顺会对车辆产生影响，使车轮受到的压力随着车辆位置变化而变化，从而改变行驶中车辆的振动状态，这种影响使车桥耦合振动问题更为复杂。因此，有必要模拟不同桥面平顺等级来研究对车桥耦合振动效应的影响。对于大跨度钢箱系杆拱桥，由于长期受日照温度的影响，导致结构内部有较大应力，产生温度变形，由此造成的桥面不平顺，也会对车桥耦合效应产生影响。为了研究二者的影响，采用了将有限元模型计算的桥面温度变形与路面不平顺叠加的方法，对车桥耦合系统的动力响应问题进行了计算与分析。

1 动力分析理论与车桥系统模型建立

1.1 结构动力特性分析方法

车辆在桥上行驶时，两者间产生动力效应是相互影响的。桥梁以无车辆荷载作用下的平衡位置为初始状态，通过子空间迭代法分析该拱桥的自振特性，由有限元法得到桥梁自身的质量矩阵Mb，刚度矩阵Kb，利用Rayleigh阻尼理论建立阻尼矩阵Cb;车辆以自重作用下的平衡位置为初始状态，根据势能不变原理求得其质量矩阵Mv，刚度矩阵Kv和阻尼矩阵Cv。车桥耦合系统中桥梁动力方程可写为：

1.2 下承式系杆拱桥有限元模型

本文以一座跨径135m的下承式钢箱系杆拱桥为背景。主梁由三片箱型钢纵梁与预制混凝土桥面板及横梁组成，横向每两道主纵梁间设置小纵梁。主拱采用三片钢箱型断面，竖直布置，拱肋為矩形等高钢箱截面，如图1所示，拱轴线为二次抛物线，矢跨比1/4。全桥共三道横撑，每7.2m设一组吊杆。下部结构采用矩形墩，承台接群桩基础。

该下承式系杆拱桥的钢箱梁采用空间板单元建模，拱肋与横撑则采用空间梁元建模，吊杆采用空间桁架单元建模。钢材弹性模量E和泊松比按现行桥梁范规取值。建立的有限元模型如下图所示：

1.2 车辆空间模型

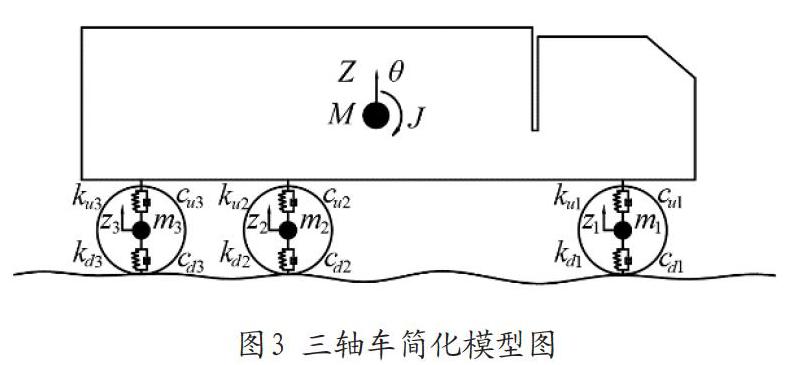
将三轴车模型简化后作为研究对象，主要参数见表1，模型包括1个车体和3个车轮4个刚体，相互之间通过弹簧和阻尼元件连接，如图3所示。M和J分别为车体的质量和绕横轴的转动惯量;m为构架和轮对质量之和;Ku和Kd分别为为上、下层弹簧的刚度系数;Cu和Cd分别为上、下层阻尼元件的阻尼系数。整个模型包括3组车轮的竖向位移、车体竖向位移、车体的俯仰角位移共5个自由度。

2 考虑温度与平顺值的车桥动力分析

2.1 桥面温度变形曲线

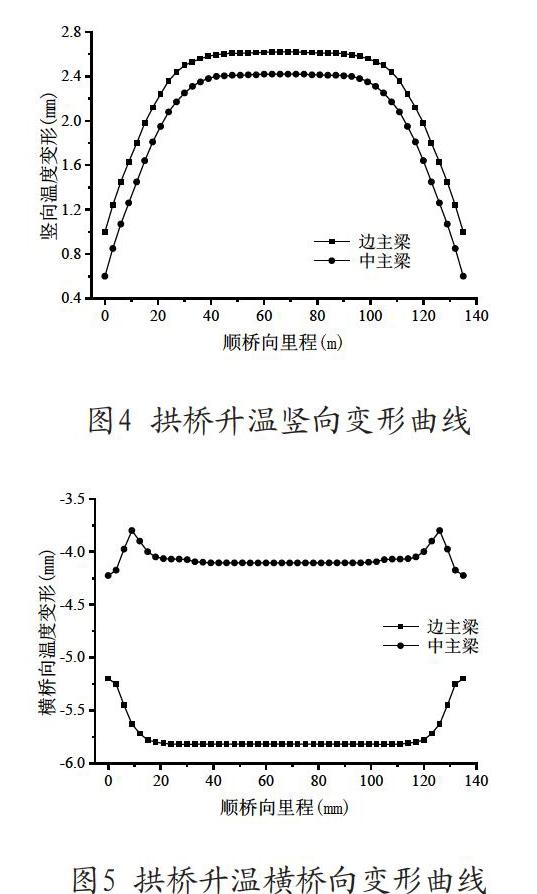
大跨径的钢结构桥梁，在温度作用下会产生一定的桥梁变形，包括季节性气温变化导致沿桥梁结构纵向均匀地伸缩和一天内太阳辐射形成的非线性日照温差变形。该桥梁地区年平均气温在15℃～16℃之间，极端最低气温-20.6℃，极端最高气温38℃以上。根据国内的《公路桥涵设计通用规范》并参考英国桥梁规范（BS-5400）利用桥梁有限元模型计算出桥面温度变形。绘出升温变形曲线如图4、5所示，降温变形曲线与其变化趋势相同，符号相反。

2.2 桥面不平顺下的车桥系统动力分析

二期铺装后桥面存在一定的不平顺，由此对行驶车辆的振动状态产生影响是车桥耦合振动的重要原因[9]。桥面的不平顺是一个空间随机过程，有着很大的不确定性。为了精确地模拟车桥动力问题，目前常用功率谱密度函数来描述路面的不平顺，将路面不平顺模拟为一个均值为0的Gauss随机过程，通过三角级数叠加法可模拟得到路面不平顺样本。本文用不平顺系数分别为（0.24，0.62，2.5，10，16）×10-6m3/cycle模拟的结果将桥面粗糙度划分为5个等级，1～5级分别对应路面状况很好、好、一般、差及很差。根据车桥系统模型和计算原理对车桥空间振动响应进行计算，结果如图5、6、7所示。

图5为不同桥面不平顺等级下，主梁和拱肋跨中部位不考虑温度变形与考虑温度变形的动力响应图。图6为不同桥面不平顺等级下，主梁和拱肋1/4跨位置不考虑温度变形与考虑温度变形的动力响应图。图7为不同桥面不平顺等级下，不同位置吊杆在考虑桥面温度变形与否条件下的动力响应图。

由结果可知，车桥系统动力响应大小主要与桥面的不平顺等级有关，桥面温度变形对其也有影响。随着桥面不平顺等级的增加，车桥系统的动力响应的变化是非线性的，整体变化规律成增大趋势。桥面越不平整，各个部位的动挠度均增大。因此，在桥梁运营期间，及时对桥面的坑洼进行整修，对保证结构安全和减少车辆的冲击作用是很有必要的。

温度变形对大跨径钢箱系杆拱桥的车桥动力响应偏于不利。高桥面平顺等级下温度变形对钢箱主梁和钢拱肋动力响应的影响要大于低桥面低平顺等级。对拱桥不同位置的动力响应进行对比分析：主梁的动力响应大于拱肋的动力响应，跨中位置要大于1/4跨位置;吊杆也是如此，跨中吊杆的动力响应大于端部吊杆的动力响应;端部吊杆在随着桥面不平顺等级的增加，温度变形对动力响应的影响总体要大于对跨中吊桿的影响。下承式系杆拱桥的跨径越大，受冲击效应的影响也越大，在大跨径桥梁结构的设计中，应考虑温度变形和桥面不平顺度对车桥耦合效应的影响。

3 结论

文中以跨径135m的下承式钢箱系杆拱为例，利用有限元法，模拟考虑温度变形和不同平顺等级下车桥耦合振动效应，得出：

（1）车桥动力响应均随路面不平顺等级的增加而非线性快速增大。不同路面等级下的各位置对应的动力响应相差较大。在大跨度拱桥结构设计中，考虑不平顺等级对车桥耦合的影响是必要的。

（2）拱桥不同部位对动力冲击效应的敏感程度不同，总体上有吊杆>主梁>拱肋的趋势。拱桥主梁和拱肋在跨中的敏感程度要高与1/4跨位置。

（3）温度变形使桥梁动力响应增大，对拱桥车桥耦合系统的影响是偏于不利的。

参考文献

[1]王贵春，李武生.基于车桥耦合振动的车辆舒适性分析[J].振动与冲击，2016，35（8）：224-230.

[2]赵露薇，王贵春，李华阳，等.大跨度钢管混凝土拱桥的动力冲击系数分析[J].结构工程师，2019，35（2）：14-20.

[3]陈代海，李整，刘琼，等.公路桥梁2种车桥耦合振动分析方法的对比研究[J].铁道科学与工程学报，2017，14（7）：1449-1456.

[4]Ding Y，Zhang W，Au F T K.Effect of dynamic impact at modular bridge expansion joints on bridge design[J].Engineering Structures，2016，127：645-662.

[5]Kim C W，Kawatani M，Kim K B.Three dimensional dynamic analysis for bridge-vehicle interaction with road roughness[J].Computers & Structures，2005，83（19-20）：1627-1645.

[6]朱劲松，邑强.中下承式拱桥吊杆应力冲击系数不均匀性研究[J].振动与冲击，2012，31（13）：5-10.

[7]李小珍，张黎明，张洁.公路桥梁与车辆耦合振动研究现状与发展趋势[J].工程力学，2008，26（3）：230-240.

[8]周德，叶梅新.高速铁路下承式钢箱系杆叠拱桥的受力分析[J].钢结构，2009，24（5）：42-47.

[9]邵元，孙宗光，陈一飞，等.车辆荷载对中承式拱桥吊杆体系的冲击效应分析[J].公路交通科技，2016，33（1）：82-88.

[10]中华人民共和国交通部.JTG D60—2015公路桥涵设计通用规范[S].北京：人民交通出版社，2015.

[11]蔡军哲，何伟，边陇超，等.车-桥耦合振动的动力响应分析[J].大连交通大学学报，2015，36（4）：22-26.