思想无界行动有向
2020-07-09张范辉
张范辉
摘 要:“智”一般指人们认识世界的能力,教学中就是对主体对象——儿童——思维水平的概括。数学是理科,“理”特指数学知识的内涵本质,是对数学学科知识与思想的概括,指教学的载体对象知识。教学改革的有效性取决于对主客体这样的客观要素认识与优化程度,只有在两者的互孕互促互化中,数学教学才能生动创造、开放凝聚,走向美的境界。
关键词:智慧;自由;理性;小学数学教学
教育如农事。农民的价值在田野,教师的价值在课堂。農事需深耕,教育需改革。“课改”首先需“改课”,教无定法、“我的课堂我做主”可以让教师有足够的自主权,改变教学理念,重组知识结构、变更呈现方式等,从而可以走向“形散”。形散意味着教学思想灵动、思维触角自由,可以探摸更远的地方,引领儿童自由发现与创造。教师们常说的“智”就是人们认识世界的能力,在教学中就是对学习主体——儿童——思维水平的概括。
但“形散”也并非信马由缰,教无定法之下,却有常法,贵在得法,这里的“法”自然首先是方法,更深的理解还应是方向,贵在有明确的方向,鲜明导向之中寻求合理的方法。形散中透着神聚,神聚意味着数学课堂主题内核明朗、思维路径清晰、教学结构合理、思想蕴涵澄明,在自由创造中有明确的方向,这个方向就是思维的锤炼、素养的提升、理性的形成,诚如史宁中教授所说,“判断数学基本思想的原则有两个,第一是数学产生和发展所必须依赖的那些思想,第二是学习过数学的人应当具有的基本思维特征”,这个思维特征就是数学“理性”,这也就是人们常说的数学是理科,而不同于语文等其他学科的思维特征,“理”就是对学习载体——数学学科——知识与思想的概括。
有效的教学改革必立足于客观要素的优化。着眼教学中主体之“智”和载体之“理”的客观对象,把数学知识冰冷的学术形态不断转化为火热的教学形态,创造出师生理解、内化知识的一段段美丽的学习时光。
一、智理互孕,教学要利于学生有新发现
数学是客观性地存在,还是人类观念性地存在?绵延千年的“心实之争”让人们拥有了不同的思考视角与深刻的洞察眼光。争辩的过程也就是主体的思考之智与载体的知识之理互孕互长的过程,这样的争辩也就让“内心的法则”与“头顶的星空”都成为能够震撼心灵的理性力量。
如何看待数学知识的眼光,能够带来教学方法的转变?很多人认为,数学知识客观冰冷,高度的抽象性与逻辑的严谨性容不得半点质疑、半点虚假,似乎只有呈现冰冷才是理性真正的面貌。以至于感性的、活泼的儿童在进行四则混合运算中,多次犯错而不能纠偏的情况下,询问老师“干吗非得要先乘除后加减”。是啊,冰冷的规定背后到底有着怎样火热的思考?一段时间让笔者迷惑德国数学家格奥尔格·康托尔曾说“数学的本质就在于它的充分自由”,其思想意义是怎样的?数学的概念、符号难道真的就是这样枯燥么,就不能天马行空么?
最简单的自然数“1”是生来就这么规定的么?为何楔形文字、罗马文字中的“1”不是这样的呢?史宁中教授曾说,如果历史可以重来,今天的数学还是这个样子么?史教授自己的回答是,大概除了1加1等于2这样的运算法则不变,其他的几乎全部可以改变。“1”本身并不存在,作为抽象符号表达,首先是想象与演变的结果。随着人们的智慧创造,不断被赋予了新的内涵,越来越具备了更深的思想。创造出的“1”,从开始仅仅表示的一个物体,继而成为一个整体、一个单位,从计数到测度,从有限到无限,其中所蕴含着的巨大创造性与思想性,每每让人叹为观止。《道德经》言“道生一”,从中可以感悟到“1”的创造是如此玄妙,以“道”字道出无法言传的玄妙。德国数学家克罗内克尔曾说:“上帝创造了自然数,其他都是人造的。”笔者想克罗内克尔要表达的应该是:上帝创造了一,然后由人创造出了二、三以及其他。
最基本的图形“点”,按《几何原本》的说法,“点是没有部分的”,意味着点除了位置之外什么都没有,按此定义,哪里能找到点?用笔画在纸上的点就是数学上的点了么?眼中看到的点就是真正意义的点了么?再细尖的笔,把点画到纸上,就已偏离点的本意了,因为这是面,只不过看上去很小而已,但面对它,我们都会清楚地认为这是一个点。测量的常识就是首先把所测量物体的两端看作两个点:测量线段的长度,把线段的两端看作两个点;测量两城的距离,我们常把两城作为两个点;测量地球到月球的距离,我们把地球与月球看作两个点……这时,点早已是一种想象。“抽象的前提是想象”,这般一看,数学还冰冷么?还客观么?但这般想象毫不妨碍纯粹的思考。点动成线,线无粗细、无颜色,但我们同样用各种笔画出缤纷的、不是线的线,在丰富的想象之中进行着严格的定义。线动成面,面动成体……人们运用想象与推理的智慧,构建了完整的图形知识体系,严丝合缝,严密理性。
“1”与“点”作为数与形的两个最基本概念,其诞生与发展的过程,就是人们的智慧创造与知识的理性内涵不断生发、生长的过程。数学所研究的数量关系、空间形式都是智理互孕、互生互长的结果,丰富而又有秩序,一切都井井有条、合理美妙,经由不断的抽象与推理,最终构成了严谨理性的数学体系。如此,解读康托尔表述数学的本质是自由,其内在含义不仅是数学发展过程中所展现出的“自由创造”,更为重要的是,数学在寻求其严谨的同时,表现出极大的开放性和创造性。那么,教学就遵循着这样的规律去创造和开发吧,让儿童拥有新眼光,善于新发现。
二、智理互促,教学要利于思维有新发展
数学起源于以认识世界为目的的哲学,必然具有认识世界所需的方法论。儿童数学素养提升的显要标志是解决问题的思维与方法,而这也就是认识世界的方法论视角。
明理能生智。“运算能力”的培养上,在理解运算的基本知识、理清数量关系基础上,能够抓关键、灵变换、简过程、优运算,生发出惊艳的智慧之花。对于如64+72×8这样的计算,如果以基础算法,先乘后加,按步计算得结果。但如果能对数理理解清晰,则会生发64+9×8×8,得到64+9×64,进而得到10个64是640的巧妙算法。显然在这过程中,需要的是数感、口算水平以及对乘法分配律算理的深入理解,对于数理的透彻理解,捕捉住隐匿联系,促进方法活用,显现优化的计算能力,这就是思维水平的提升,形成智慧火花。
“空间能力”的培养上,在理解图形的基本概念、掌握图形间相互关系基础上,能够灵活变换、简约过程。
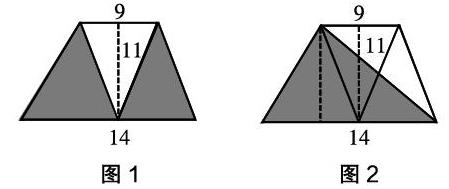
面对如图1的阴影部分面积计算的问题,按常规计算办法,阴影部分的面积应是用梯形的面积去掉空白部分三角形的面积,即(9+14)×11÷2-9×11÷2。但细察发现,阴影部分的两个三角形等高,如图2所示,可以把阴影的两个三角形转化为一个大三角形,直接由14×11÷2得到最后的结果。这是对平行线的性质、等底等高三角形的面积相等等图形之理明晰的基础上,生发出的巧妙方法。优化的方法中,我们可以看到,由各图形面积计算的方法(认知),分析图形间的联系(明理),形成判断、运用策略、优化方法、发展思维(成智)。
从这里的数与形的两个案例中,我们可以感悟到,数学知识内在之理的透彻理解,优化方法策略,促进思维发展、智慧生发。
反之,人们的智慧提升又进一步促进数学发展。几何学发展历程,从欧式几何的概念必须建立于现实常识到非欧几何概念建立于逻辑公理,甚至有些概念有悖于人们对熟知世界的认识,数学的自由表现挣脱了现实的束缚,人类的思想可以无限制、无边界的向外拓展,但无界的思想却有着严谨的逻辑。如今几何学的概念、结论早已与是否符合客观实际无关,只要它符合逻辑推理。这就是典型的人的智慧促进数学的发展,目前看,不管数学的发展如何分支,但数学整体一致,结果相互协调,蕴含着真理的内涵。
三、智理互化,教学需启迪心智新成长
和所有知识一样,数学知识是人所创造的,必将带着人文的底色。一方面,是人创造了数学知识,经过不断遴选形成较为完善的学科体系,构成学生学习成长的载体,数学知识凝结着人类的智慧、思想与精神。另一方面,形成的数学学科又以独特的内涵思想、理性力量重塑人的自身。这样的主体之“智”与载体之“理”互化就体现了人文的两个维度,即以人创文,文以化人。数学化人的角度是独特的、理性的,带着生动、深刻的意味。
对于用“数手指”辅助做算术题,较多小学低年级的教师认为不可取,他们认为这种方法可能对孩子的计算造成心理上的“手指依赖”,从而导致浅于数理分析、弱于口算技能,不利于培养孩子的数感,因而在一开始即严格按照数的分合等来开展算术教学,同时不允许学生“数手指”。但对于心智发展稍微延后的儿童,与其限制造成的躲躲闪闪、欲“数”还休,还不如科学地利用好天然“工具”来更好地进行计算。从一开始的“掰手”数指进行计算,即边掰手指,边看边数完成算术运算;逐步到“背手”数指进行计算,即把小手放在自己的背后,可伸拨手指,通过思考而不是直接看着手指帮助完成运算;最后“想手”数指进行计算,即在自己的脑海中形成“手指表象”来完成算术运算。这三个阶段也正是孩子经历从具象到表象,再到抽象的过程,这个过程中,还可以通过“5”这一数字渗透初步的“整体”意识。
人生各有差异,这是客观的,也是这个世界丰富多彩的原因。运算结果虽一致,但过程方法各不同。在不同的过程中寻求启迪心智成长的普遍方法。数学化理成智的过程是独特的,从直观到抽象,从特殊到一般,启迪智慧,发展心智。
面积和长度、角度、体积一样,除了测量对象的维度不同,其“确定单位、测量对象、得到结果”的思维本质是一样的。长度的测量,是用一段规定的、已知的单位长度去不重叠地依次测量多次,然后把所量的几段长度相加得到最后的结果。与此类似,面积的测量则是用一块规定的、已知的单位面去不重叠地依次覆盖所要测量的面,然后相加得到最后的结果。这样的先“1”后测,这样的“有限可加性”揭示着数学测量的本质意义,这个数以多少为合适、用哪个单位作表征,说到底只不过是根据测量所要解决什么样的问题而定。如此“定单位、去测量、得结果”的测量意识、认知与能力就是人们生存、生活的一种基本素养,成为观察与认识世界的普适眼光与解决问题的基本能力,这也就是为什么要人人学习数学、人人都要具备基本数学眼光的道理所在。数学化理成智的视角是普适的,心智的成长就是面对新问题时的方法迁移解决的过程。
未来已来。以不确定性為特征的时代呼唤创新型人才的要求,我们的应答就是基于学科来育人、树人。华为创始人任正非所言“未来就在小学教师的讲台上”,雷霆之语折射出的是培养什么样的人、怎样培养人这样的本源追问。数学教师立足课堂主阵地,丰富开放的生动智慧,严谨普适的深刻理性,教学过程体现着华东师范大学汪晓勤所倡的“知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效”。以数学之理培育儿童之智,从而让数学教育创造属于未来的生命之美。
