40 t 无砟重载铁路隧底结构设计参数研究
2020-07-09苗德海王克金高建国余俊周涛
苗德海,王克金,高建国,余俊,周涛
(1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063;2.中南大学 土木工程学院,湖南 长沙 410075)
重载铁路运输是当今铁路发展的重要方向之一。大轴重载运输具有运能大、效率高、运输成本低及机车车辆运转效率高的特点。因此,重载铁路运输是大宗货物及最为经济有效的运输方式,但在建和已建成的重载铁路隧道会有因基底结构承受重载列车荷载而出现较大的病害隐患。目前,国内外研究一般为30 t 轴重以下的重载铁路,30 t 以上的研究鲜见。朱波[1]基于大轴重重载列车荷载作用特征,运用轨道路基动力学分析原理,以动强度、支承刚度和长期稳定性为设计原则,开展了大轴重作用下重载铁路路基结构设计方法的研究。李自强[2]通过现场实测明确27~30 t 轴重和III~V 级围岩条件下有砟、无砟的单、双线重载铁路隧道结构的动力特征。邹文浩[3]等人以某重载铁路隧道工程为依托,结合现场实车试验和数值模拟,研究30 t 轴重列车荷载作用下重载铁路隧道基底结构的应力分布和动力响应。杜明庆[4]建立了高速铁路隧道仰拱安全性分析模型,提出了以隧道围岩性质与仰拱结构条件、静力响应及动力响应3 个指标的评价模型,建立了包含破坏模式、隆起位移、裂缝开度、裂缝深度、裂缝长度、振动加速度及振动损伤7 项基础指标在内的综合评价体系。宋洪锐[5]分析得到了行车速度、道床板宽度、道床板厚度、隧道基底刚度等参数对重载车辆无砟轨道系统动力学性能的影响规律,并提出了重载铁路隧道无砟轨道结构参数的合理值。刘聪[6]等人根据重载铁路隧道底部疲劳关键部位的力学特性,开展双侧限高静载低动载波动疲劳试验,得到了重载铁路隧道底部结构试件的最大拉应变和电导的演化规律。Dawn[7]等人对英国铁路路基振动反应进行了测试,研究了列车速度、激振频率同轨道参数之间的关系。Jackobsen[8]通过由列车荷载引起的地面振动的现场测试,得到了地面振动水平与相关轨道参数间的关系。
目前,国内外对在40 t 轴重荷载作用下的基底结构动力响应特征及累积损伤特性的研究鲜见。因此,以几内亚西芒杜矿山铁路为背景,线路全长约657 km,为内燃单线重载铁路,设计轴重采用40 t,主体结构按满足75 a 使用年限的要求进行设计。2座特长隧道地层岩性以花岗质片麻岩为主,洞身局部为花岗岩,弱风化为主,工程地质条件好。隧道采用单线无砟轨道,隧道衬砌内轮廓如图1 所示。本研究根据几内亚西芒杜矿山铁路的地质参数对40 t 轴重单线无砟重载铁路隧道施工的关键技术进行模拟分析。
1 计算原理及条件
1.1 计算方法
根据地层-结构计算模型进行模拟分析,并采用ABAQUS 有限元软件建立隧道-围岩耦合二维计算模型。同时,考虑隧底围岩的累积损伤机理和隧底混凝土结构的损伤塑性特性,针对隧底围岩与混凝土结构分别采用了非定常数流变损伤本构模型[9]与混凝土损伤塑性CDP 模型[10]。
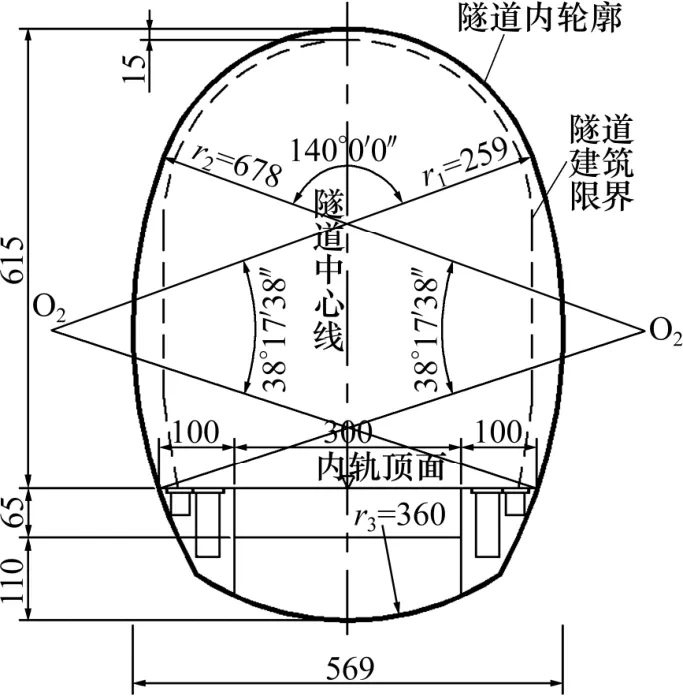
图1 隧道衬砌内轮廓Fig.1 Inner outline of tunnel lining
1.2 计算模型
模型水平方向以隧道中线为中心,向隧道左右各取100 m;竖直方向自隧道仰拱中心向下取60 m;自隧道拱顶中心向上取至地表,地表埋深按深埋考虑,取54 m。采用有限元计算软件ABAQUS 建立模型,左、右两面施加横向约束,底面为固定边界,上表面为自由边界,整个模型施加竖直向下的重力,围岩的初始应力全部由地层的自重应力产生,模型采用平面四节点单元模拟。计算模型及网格划分如图2 所示。

图2 模型网格划分Fig.2 Mesh generation of the model
1.3 列车荷载
采用激励力函数[11]对重载列车荷载进行模拟,激励力函数考虑了静荷载与振动荷载的叠加作用,并考虑了列车轮对力的叠加组合和钢轨与轨枕的分散传递。其中,振动荷载反映了不平顺和轨面波形磨耗效应等影响因素[12],其计算式为:
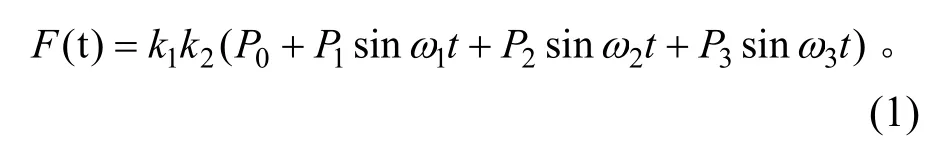
式中:P0为车轮静载,N;P1,P2和P3分别为行车不平顺、动力附加荷载和波形磨耗等相关的典型振动荷载值,N;k1为轮轨力叠加系数;k2为钢轨分散传递系数;t为时间,s;ai为典型矢高,mm;ωi为不平顺控制条件下的振动圆周率,其表达式为ωi=2πv/Li,v为行驶速度,m/s,Li为轨道几何不平顺波长管理值,m(见表1)。
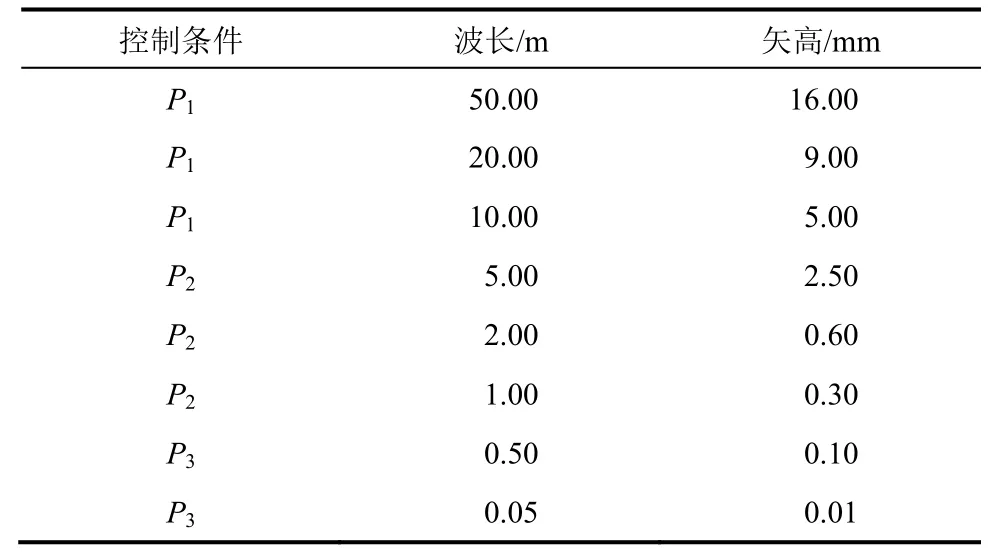
表1 英国轨道几何不平顺管理值Table 1 Management value of track geometric irregularity in UK
振动荷载幅值为:

式中:m为列车簧下质量,kg。
根据激励力函数可以得到40 t 轴重的列车动荷载,如图3 所示。
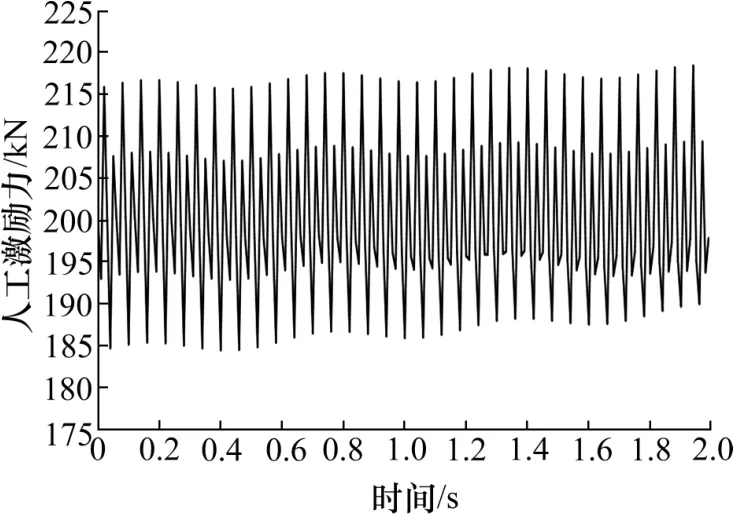
图3 40 t 轴重列车荷载Fig.3 Train load of 40 t axle heavy
1.4 非定常数流变损伤本构模型
Ⅲ~Ⅴ级围岩的弹性模量、泊松、重度、粘聚力及D-P 摩擦角等材料参数依据《工程岩体分级标准(GB/T50218—2014)》[13]确定。
在重载列车高速运行下,隧底围岩存在累积损伤现象。本研究采用基于变参数流变损伤的本构模型[9],该模型将岩体流变力学参数看作是非定常的,认为岩体流变参数随时间逐渐弱化,从而直观反映材料的损伤劣化过程。其计算式为:
当σ0<σf时,线性黏弹性蠕变:
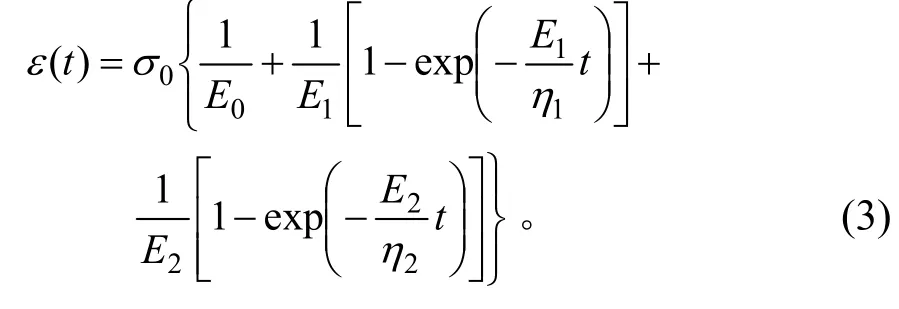
当σ0<σf时,非线性黏塑性蠕变:
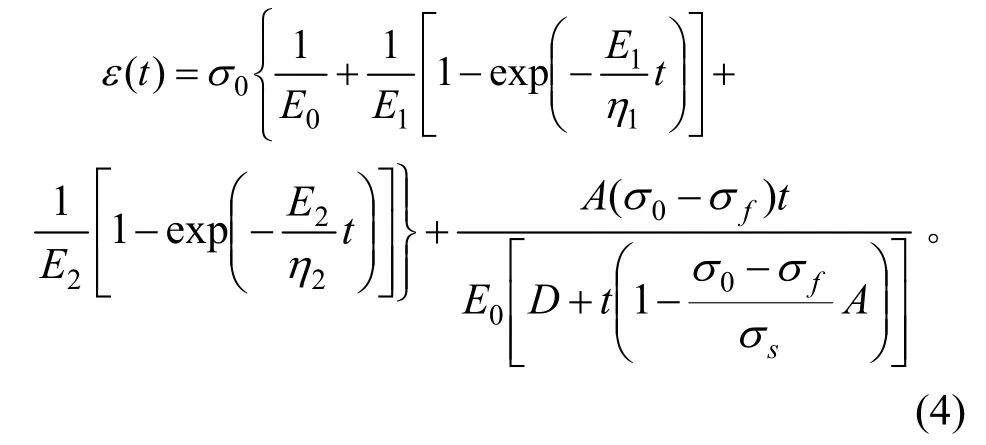
式中:E1,E2为广义Kelvin 体弹簧元件的弹性模量,MPa;E0为初始弹性模量,MPa;η1,η2为广义Kelvin体黏壶元件的黏滞系数;σ0为屈服应力,MPa;σf为长期强度,MPa。
将式(3)与式(4)中的E0换成Ei,即为变参数流变损伤本构模型的蠕变方程:
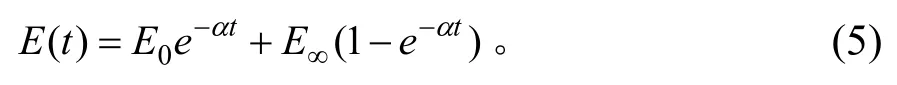
式中:E∞为长期弹性模量,MPa;α为与损伤程度相关的系数。
1.5 混凝土损伤塑性CDP 模型
隧道结构中填充层(C25)、轨道板(C45)、初期支护(C25)、二次衬砌(C35)及混凝土基础(C30)的重度、弹性模量和混凝土的抗拉、压强度标准值等材料参数依据《混凝土结构设计规范(GB50010—2011)》[14]确定。混凝土结构采用CDP 模型[10],应用比例应变(Birtle 法),其计算式:
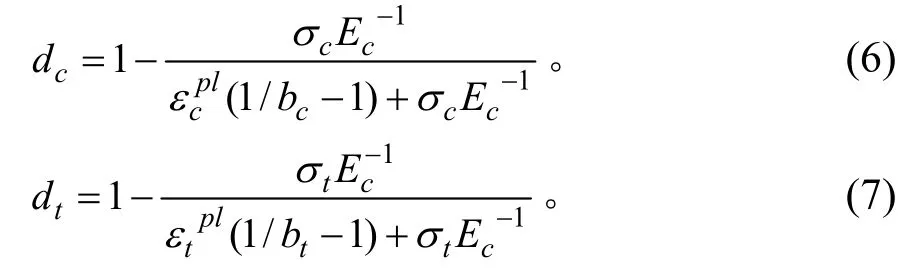
式中:bc,bt为非弹性应变中塑性应变的比例。为非弹性应变中的塑性应变;dc,dt分别为混凝土的压、拉损伤值;Ec,σc分别为初始弹性模量与受压应力,MPa。
根据混凝土单轴受拉受压应力应变曲线公式,得到相应非弹性应变下的混凝土屈服应力;然后得到应力-非弹性应变的一系列数据;最后输入ABAQUS 计算软件中进行数值模拟。
2 数值计算
在列车荷载的长期作用下,虽然重载铁路隧道上部结构和围岩受到的影响很小,但是仰拱结构出现不同程度的疲劳损伤,处于不利状态。表明:基底结构是重载铁路隧道设计的关键位置,本研究着重分析隧底结构。
在静力计算的基础上直接进行动力计算,从而实现静、动力计算的连续。先进行围岩初始地应力和隧道的开挖模拟,得到隧道开挖后动力计算之前围岩与隧道结构的初始应力和初始位移条件。然后,施加列车荷载,进行动力响应分析。其计算步骤为:
2) 分三步进行隧道开挖和支护模拟,即隧道开挖与初期支护、施加二次衬砌及轨道板与填充层浇筑。
3) 选取特征点,便于分析重载铁路隧道基底结构的动力特性。隧道选取隧底中心处、左轨道正下方仰拱处2 个特征点,如图4 所示。针对填充层与失跨比的分析,其位移分析采用仰拱中心特征点,而应力分析采用左轨正下方特征点。
4) 施加列车荷载进行隧道结构动力响应分析。

图4 隧底结构特征点示意Fig.4 Schematic diagram of the characteristics of the tunnel bottom structure
3 计算结果与分析
3.1 不同轴重下隧底结构动响应分析
为分析不同轴重对隧底结构的影响,保持隧道结构型式、支护参数等条件不变时,在III~V 级围岩下,对比分析了21,24,27,30,33,36,40 和43 t 8 种不同的轴重列车荷载作用下隧底结构动力响应特性。
3.1.1 不同轴重下隧底结构位移响应分析
分析不同的轴重对隧底结构动响应的影响,其仰拱竖向位移如图5,6 所示。
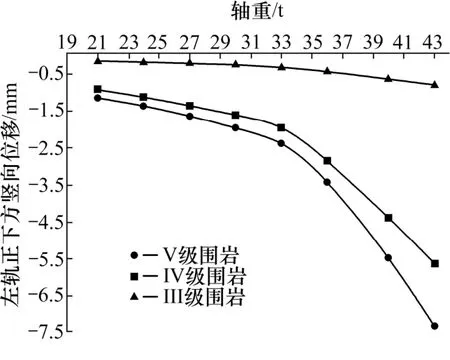
图5 不同轴重下左轨正下方的竖向位移Fig.5 Vertical displacement of the inverting arch directly below the left rail
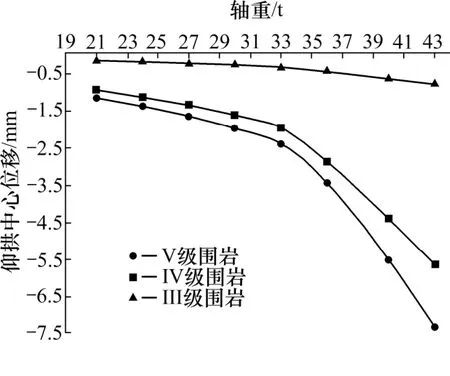
图6 不同轴重下仰拱中心的竖向位移Fig.6 Vertical displacement of the center of the invert arch
从图5,6 可以看出,对于不同围岩等级的单线无砟隧道隧底结构,轴重在21~33 t 区间隧底仰拱各特征点竖向位移响应均呈现线性增长,轴重每增加1 t,隧底中心处位移增加最大为0.103 mm,增大了8.71%;左轨正下方处位移增加最大为0.103 mm,增大了8.69%。在轴重在33~43 t 区间,隧底仰拱各特征点竖向位移响应增量呈明显的非线性增长,隧底中心处增加最大为4.942 mm,增加了204.7%;左轨正下方处增加最大为4.938 mm,增加了204.8%。计算结果表明:V 级围岩隧底仰拱各特征点竖向位移响应最大,IV 级围岩次之,而III 级围岩响应最小。所以III~V 级围岩过程中,隧底仰拱各特征点竖向位移响应均呈现明显的非线性变化且逐渐变缓。
3.1.2 不同轴重下隧底结构应力响应分析
②互相融通,优势互补。厅直水电站分别拥有不同类型的机组,有各种不同类型的技术人才,可以相互交流,互相融通,形成优势互补,容易承揽业务,扩大优势。
分析不同的轴重对隧底结构拉应力响应的影响,应力响应如图7,8 所示。
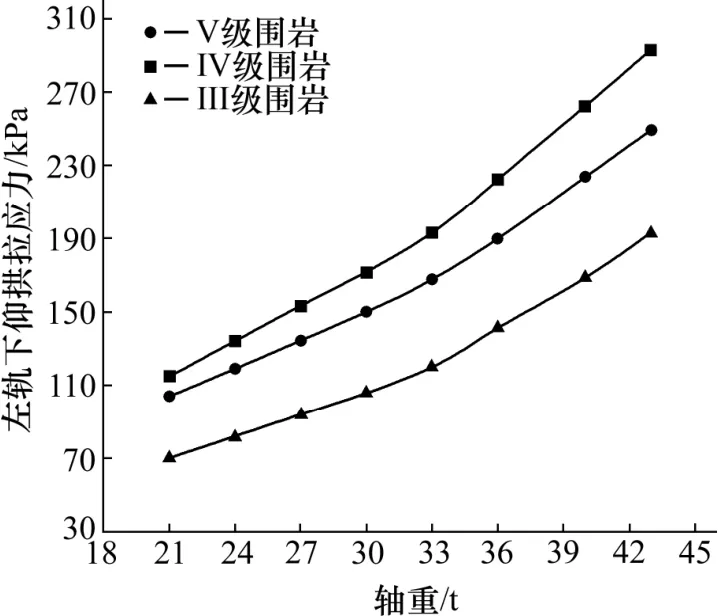
图7 不同轴重下左轨正下方的仰拱拉应力Fig.7 Pulling stress of the inverting arch directly below the left rail
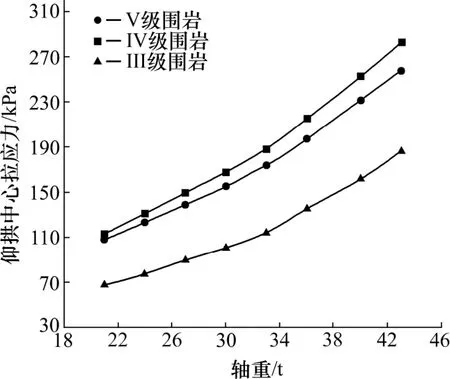
图8 不同轴重下仰拱中心的拉应力Fig.8 Pulling stress of the center of the invert arch
从图7,8 可看出,对于不同的围岩等级的单线无砟隧道隧底结构,轴重在21~33 t 区间,隧底仰拱各特征点拉应力应力响应均呈现线性增长,轴重每增加1 t,隧底中心处拉应力增加最大为6.38 kPa,增加了5.67%;左轨正下方处拉应力增加最大为6.53 kPa,增加了5.70%。在33~43 t 区间,隧底仰拱各特征点拉应力响应均呈现非线性变化,隧底中心处拉应力增加最大为93.91 kPa,增加了49.66%;左轨正下方处拉应力增加最大为100.19 kPa,增加了51.94%。表明:IV 级围岩隧底仰拱各特征点拉应力最大,V 级围岩次之,而III 级围级最小。所以在III~V 级围岩过程中,隧底仰拱各特征点拉应力响应出现跳跃但总体呈增大趋势。
3.2 不同填充层厚度下隧底结构动响应分析
为分析填充层厚度对单线无砟重载铁路隧道的隧底结构动力响应的影响,计算中只改变填充层厚度,其他结构参数不变。
计算条件:III~V 级围岩,行车速度取为120 km/h,采用40 t 轴重重载列车荷载。单线无砟隧道填充层厚度分别取0.9,1.1,1.3 和1.5 m。
3.2.1 隧底结构位移响应分析
为分析不同的填充层厚度对隧底结构的位移影响,其仰拱中心的竖向位移如图9 所示。
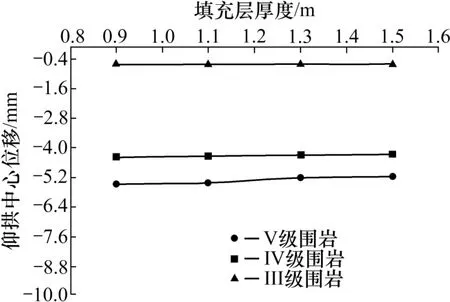
图9 不同填充层厚度下仰拱中心的竖向位移Fig.9 Pulling stress of the center of the invert arch
从图9 可以看出,不同的围岩等级的单线无砟隧道隧底结构,随着填充层厚度增加,隧底中心仰拱处竖向位移动力响应有减小的趋势,但减小的幅度较小,最大为0.302 mm,仅占5.47%。因此,隧道填充层厚度的增加,对仰拱竖向位移影响不大。表明:V 级围岩隧底仰拱竖向位移响应最大,IV 级围岩次之,而III 级围岩最小。所以在III~V 级围岩过程中,隧底仰拱竖向位移响应呈现明显的非线性变化且逐渐变缓趋势。
3.2.2 隧底结构应力响应分析
为分析不同的填充层厚度对隧底结构的应力响应影响,拉应力响应如图10 所示。
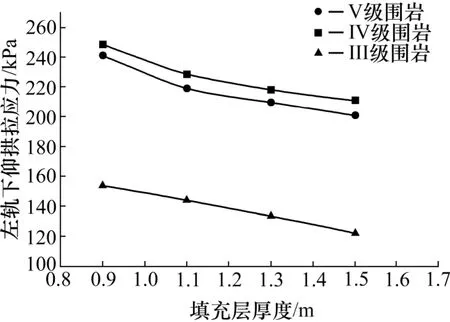
图10 不同填充层厚度下左轨正下方的仰拱拉应力Fig.10 Pulling stress of the inverting arch directly below the left rail
从图10 可以看出,不同围岩等级的单线无砟隧道隧底结构,填充厚度从0.9 m 增加到1.5 m 过程中,最大减小了16.73%。因此,随填充层厚度的增加,对隧道仰拱轨道正下方处拉应力影响越大。即填充层厚度越大仰拱最大拉应力就越小。当填充层厚度大于1.1 m 时,这种减小的趋势逐渐变缓。表明:IV 级围岩隧底仰拱各特征点拉应力最大,V级围岩次之,而III 级围岩最小。所以在III~V 级围岩过程中,隧底仰拱各特征点拉应力响应出现跳跃但总体呈增大趋势。
3.3 不同矢跨比下隧底结构动响应分析
为分析矢跨比对单线无砟重载铁路隧道的隧底结构动力响应的影响,计算中只改变矢跨比,其他结构参数不变。
计算条件:III~Ⅴ级围岩,行车速度取为120 km/h,采用40 t 轴重重载列车荷载。单线无砟隧道矢跨比分别取为1:5,1:6,1:7,1:8 及1:9。
3.3.1 隧底结构位移响应分析
为分析不同失跨比对隧底结构的位移影响,其仰拱竖向位移如图11 所示。
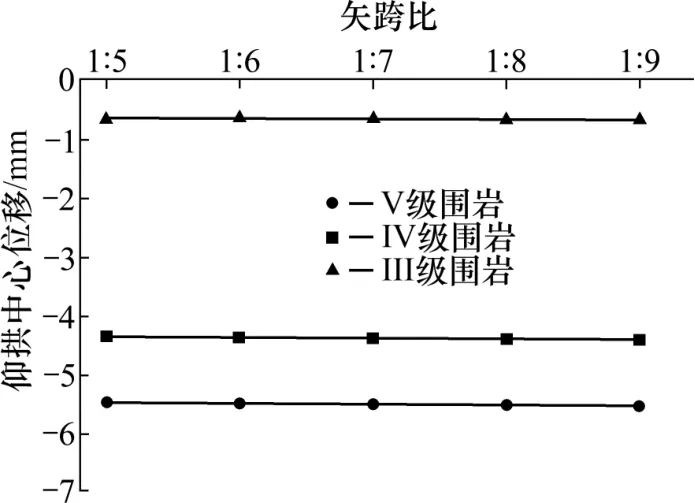
图11 不同矢跨比下仰拱中心的竖向位移Fig.11 Pulling stress of the center of the invert arch
从图11 可以看出,不同围岩等级的单线无砟隧道的隧底结构,随着矢跨比的减小,仰拱中心处竖向位移有增大趋势,但增大幅度不大,最大值和最小值相差仅为0.066 mm。表明:矢跨比的改变对仰拱中心处的竖向位移影响很小。V 级围岩隧底仰拱竖向位移响应最大,IV 级围岩次之,而III 级围岩最小。所以III~V 级围岩过程中,隧底仰拱竖向位移响应呈明显的非线性变化且逐渐变缓。
3.3.2 隧底结构应力响应分析
分析不同的失跨比对隧底结构的应力响应影响,其仰拱竖向位移如图12 所示。
从图12 可以看出,不同围岩等级的单线无砟隧道的隧底结构,随着矢跨比的减小,仰拱结构拉应力在不断增大,且矢跨比小于1:7 后,仰拱结构拉应力增加最大为24.874 kPa,增加了12.10%。表明:IV 级围岩隧底仰拱拉应力最大与V 级围岩相差不大,但IV 级围岩下的拉应力最大值大于V 级围岩。而III 级围岩的拉应力明显小于前面两者。所以在III~V 级围岩过程中,隧底仰拱各特征点拉应力响应呈明显的非线性变化且逐渐变缓趋势。
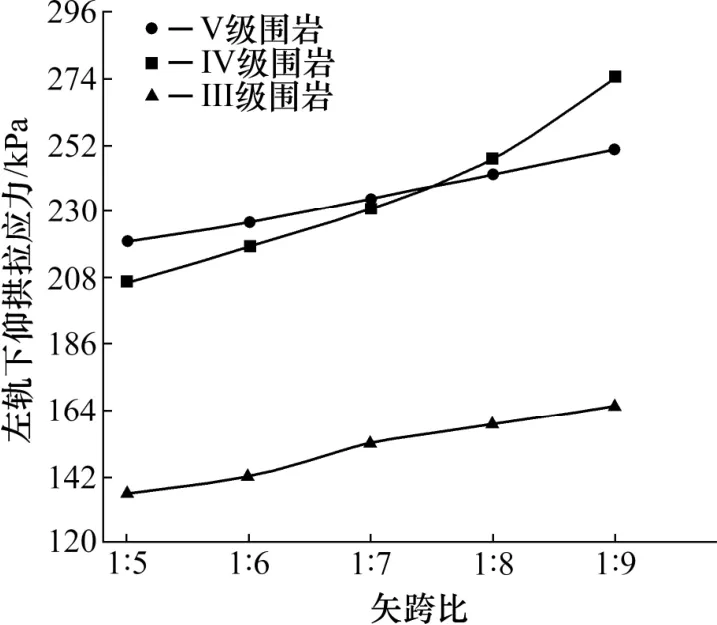
图12 左轨正下方仰拱拉应力Fig.12 Pulling stress of the inverting arch directly below the left rail
3.4 参数建议
Ⅲ~Ⅴ级围岩的单线无砟重载铁路隧底的矢跨比取≥1:7,填充层厚度≥1.1 m。
4 结论
基于隧底围岩累积损伤机理与隧底混凝土结构的损伤塑性特性,对影响隧道结构的主要参数进行研究分析,得出结论为:
1) 随着轴重增加隧道底部围岩逐渐出现流变损伤,尤其当轴重为40 t 时,隧底结构出现明显的损伤效果。因此,在隧道结构设计中,为了行车安全及隧道寿命等应当注意轴重的影响。
2) 隧底结构拉应力均在安全范围内,故基于工程施工便利与经济性原则,III~IV 级围岩的单线无砟隧底仰拱结构的矢跨比≥1:7,填充层厚度≥1.1 m。
