山区低等级公路桥梁疲劳荷载谱研究

2020-07-09苏万钦李睿刘海证李晓章

交通科学与工程 2020年2期

苏万钦，李睿，刘海证，李晓章

(1. 昆明理工大学建筑工程学院，云南昆明 650500；2. 云南省建筑工程设计院，云南昆明 650041)

车辆荷载是引起桥梁疲劳损伤的主要因素，而车辆荷载谱则是研究车辆荷载的基础[1]。英、美等国很早便开展了有关车辆荷载谱的研究并给出疲劳车辆荷载谱及疲劳车辆模型[2-3]。近年来，国内学者对此也进行了大量的研究，狄谨[4]等人统计了浙江一座港口公路桥梁1 a 内的通行车辆荷载信息，整理出了港口公路桥梁疲劳荷载谱。童乐为[5]等人基于上海市中山路桥的实测交通数据，编制了适用于上海市桥梁的疲劳荷载谱。李星新[6]等人根据贵州坝陵河大桥车辆动态称重系统(weight-in-motion system，简称为WIM)实测荷载数据，推导出了最符合梁实际受载情况的三轴疲劳车辆模型。但目前的研究主要集中在城市和高等级公路上，对低等级公路的研究相对匮乏。云南省低等级公路占了总公路里程的90%以上，且超载情况严重，加剧了公路损伤速度。研究山区低等级公路桥梁疲劳荷载谱对低等级公路桥梁的评估和维护具有重大的意义。本研究利用WIM 系统，采集云南省道S306 峨德河桥连续29 d 的车辆荷载数据，拟通过聚类分析法划分调查车辆，并分析了代表车型的车辆和车重分布特性[7]。再基于损伤积聚理论和等效损伤原理制定出山区低等级公路专用疲劳车辆荷载谱[8]，并对其简化后推导出标准疲劳车。

1 交通荷载调查

峨德河桥位于云南省玉溪市新平县境内，桥梁横跨戛洒江，是连接新平县江东和江西2 个片区的交通枢纽。利用其配备的WIM 可实时监控和统计通过该桥梁的车流的车轴数、车轮数、车辆尺寸、质量和数量等数据。

经过连续29 d(2018 年3 月)的监测，剔除了受不良因素干扰或WIM 系统本身缺陷[9]导致异常的数据后，一共获得49 199 辆车的样本数据。其中，V1～V16 为二轴车、V17～V22 为三轴车、V23～V27为四轴车、V28～V29 为五轴车及V30～V33 为六轴车。参考《中国汽车车型手册》[10]，根据轴数、轮数、乘客数(客车)或满轴载荷分配(货车)、车辆尺寸及最小离地间隙对车型进行分类，依此将该公路上的车型分为33 种，其中，有9 种客车车型(V1～V9)和24 种货车车型(V10～V33)。

2 交通荷载聚类分析

2.1 聚类分析指标

选取车轴数、车轮数、体积形状、最小离地距离[11]、客车座位或货车吨位、破坏系数以及车辆折算系数作为聚类分析指标[12]。

车轴数、车轮数、体积形状、最小离地距离由WIM 系统监测所得；客车座位及货车吨位通过查询《中国汽车车型手册》[10]可确定。

破坏系数为轴重对道路、桥梁等的破坏程度，其计算式为：

式中：n为车辆的轴重，t；n0为标准轴量，取10t；m为计算常数一般取4.55。

车辆折算系数是表征各类车辆占用道路程度的系数，参考《云南省公路情况调查》[13]进行整理。

2.2 聚类分析结果

运用spss19 统计分析软件对7 个指标进行聚类分析。其中，组与组之间考虑平均联结及度量标准使用区间平方 Euclidean 距离，得出各代表车型之间关系的树状图，如图1 所示。

图1 使用平均联结(组间)的树状Fig.1 Treemap using average joins (between groups)

从图1 可看出，样本可分为4 类，分别是{V1-V7,V10-V15}，{V8,V9,V16-V22}，{V23-V29}和{V30-V33}。考虑到V1～V9 为客车，V16 为二轴车，所以将V8、V9、V16 归入第一类车；V28 和V29为五轴车，所以将其从第三类中分出，归入第四类。因此，样本最终为5 类，分别为{V1～V9, V10～V16}、{V17～V22}、{V23～V27}、{V28～V29}及{V30～V33}。于是，将云南省低等级公路车型划分为5 类，见表1。

2.3 车型比例分析

将有效车辆样本车型归类后，得到第一类车辆有46 966 辆，占95.46%；第二类车、第三类车分别为885 辆和887 辆，各占1.8%；第四类车辆有225 辆，占0.46%；第五类有236 辆，占0.48%。与高等级公路对比，低等级公路的通行能力有限，其二轴车是低等级公路的主要通行车辆，随着车辆轴数的增加，车辆比例逐渐减小。

2.4 车重分布特征

据研究表明：交通流的车重数据一般服从正态分布、对数正态分布、威布尔分布、伽马分布及高斯混合分布等[12]。本研究先假设车重服从前4 种分布，然后通过极大似然估计法求得具体的相关特征参数，并使用K-S 检验表(显著水平取0.05)对每类分布及得到的结果进行假设检验，确定分布类型和概率密度函数。若车重数据均不满足这4 种分布方式，则通过MATLAB 中的最大期望(EM)算法，拟合得到多维高斯混合分布曲线。车重分布特征分析过程见表2，K-S 检验结果见表3。

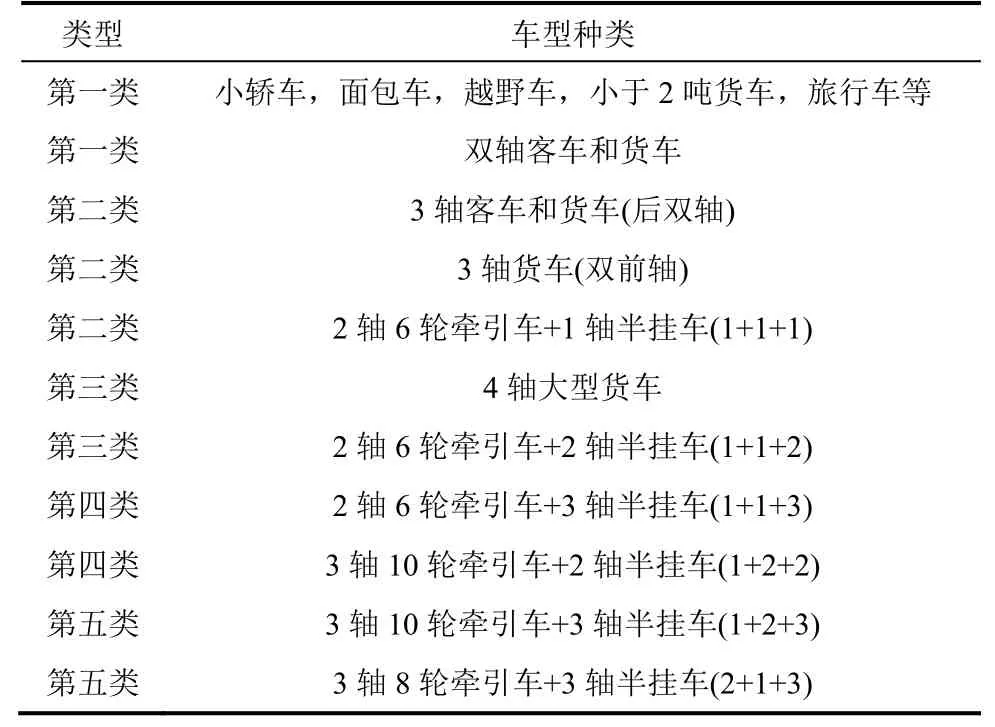
表1 云南省低等级公路交通车型分类表Table 1 Classification of low-grade highway traffic vehicles in Yunnan Province

由表3 可知，除第一类车重服从对数正态分布外，其余4 类均不满足这4 种分布类型。通过EM算法计算得到其余4 类车重服从三维高斯混合分布。5 类车型概率密度函数分别为式(2)～(6)，拟合结果如图2 所示。

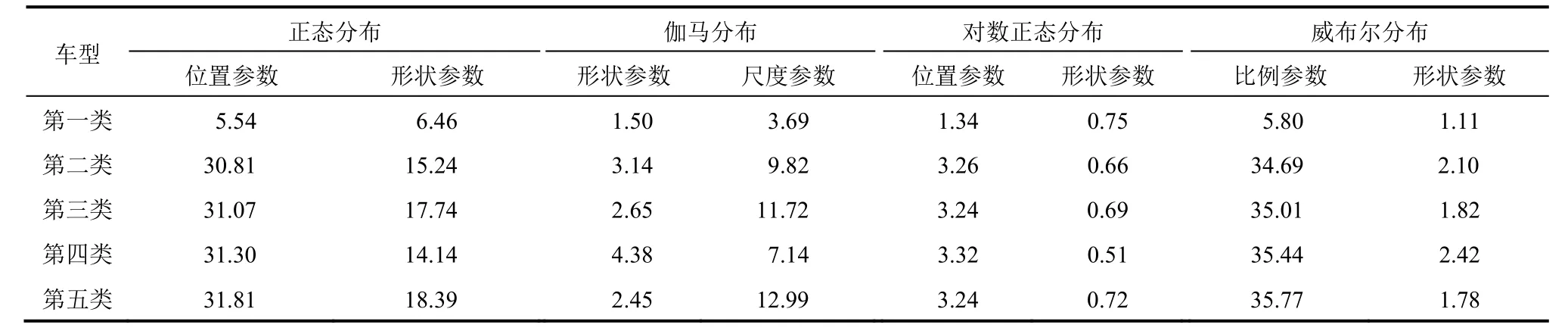
表2 车重分布特征参数Table 2 Vehicle weight distribution characteristic parameters

表3 K-S 检验过程Table 3 K-S inspection process

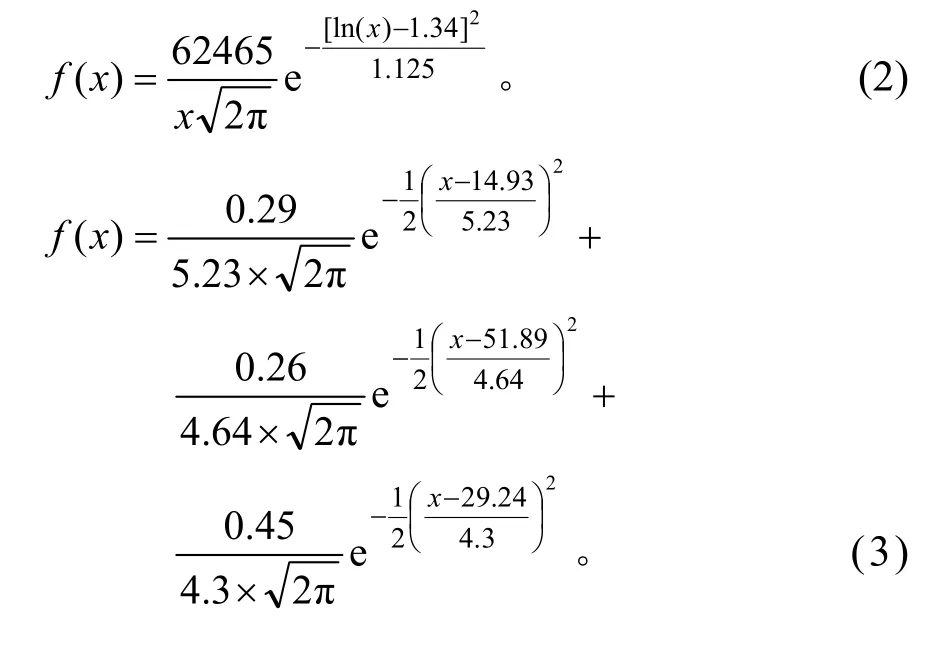
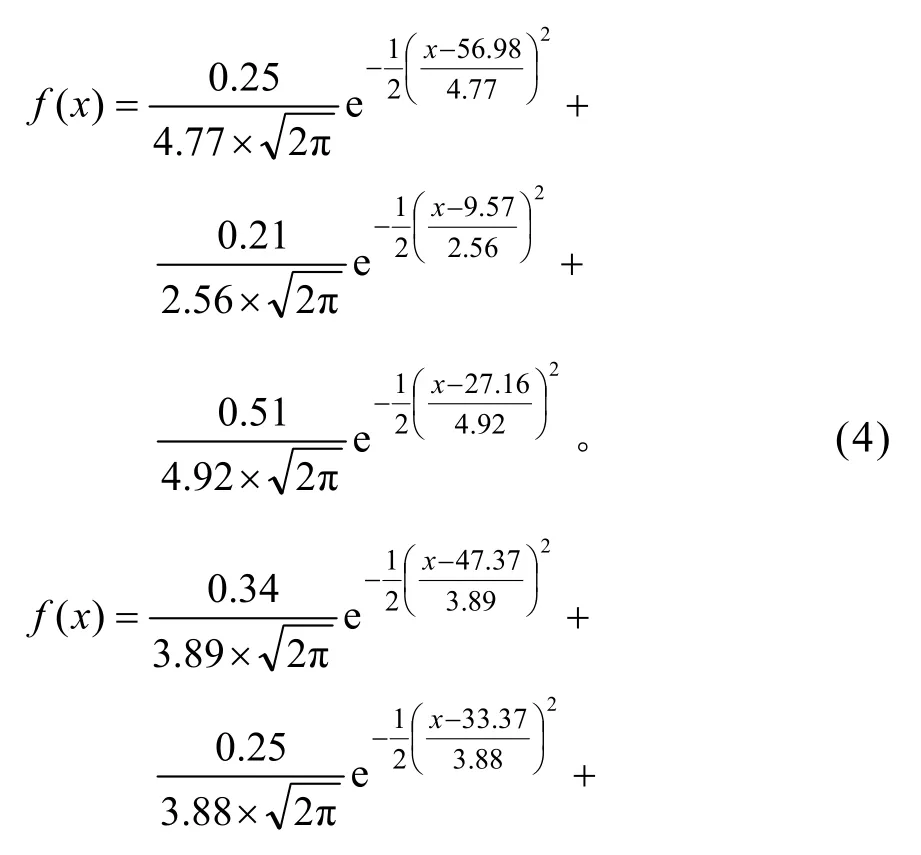
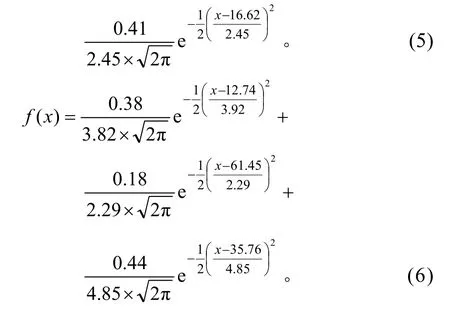
式中：x为车重，t。

除第一类车重服从对数正态分布外，其余4 类皆服从三峰正态混合分布，第一类车主要为两轴载客车辆与部分小型货车，其余4 类车以货车为主，根据《汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值(GB1589-2016)》[14]规定二轴车至六轴车最大允许总质量分别为18,25,35,43 和49 t，第二类至第四类车型函数拟合图的三峰分别对应货车空载状态、正常载货状态及超载状态。因此，图2 符合车辆实际运营情况，并且可以看出货车超载严重，第二类和第三类车超载率极高，这对桥梁的正常运营造成了极大的安全隐患。

3 疲劳荷载谱分析

3.1 典型车辆荷载谱

将调查所得33 种代表车型和5 类划分结果对应分析，根据聚类分析结果整理出超过30 kN(除V1～V3 和V10～V11 外)的云南省低等级公路上的典型车辆荷载谱，如图3 所示。

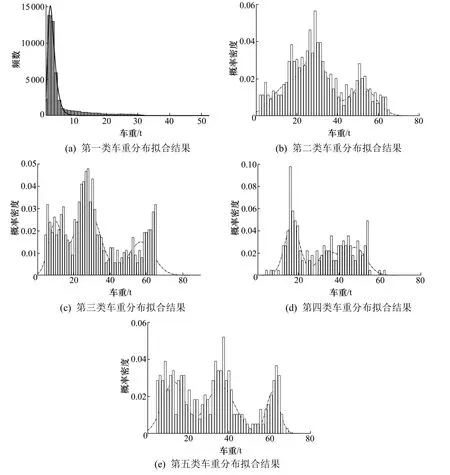
图2 各类车重分布拟合结果Fig.2 All types of vehicle weight distribution

3.2 专用车辆荷载谱

基于损伤积聚理论和等效损伤原理，分别对5类车型进行轴重和轴距的等效计算，获得每类车型中对桥梁损伤加载影响最大的代表车型，并基于此便可推导出专用疲劳荷载谱。

等效轴重和等效轴距[15]分别按照式(7)和(8)进行计算。

式中：fi为第i辆车在同一类车型中出现的频率；Wij为第i辆车的第j个轴的轴重；Wεj为该类模型车辆第j个轴的等效轴重；m为钢结构构造细节S-N疲劳曲线的斜率，取值为3。

式中：Aij为同一类车型中第i车辆的第j个轴距；Aj为分类模型车辆的第j个轴距。

根据式(7),(8)分别计算各类车的等效轴重和等效轴距，得到专用车辆荷载谱，如图4 所示。

3.3 标准车辆荷载谱

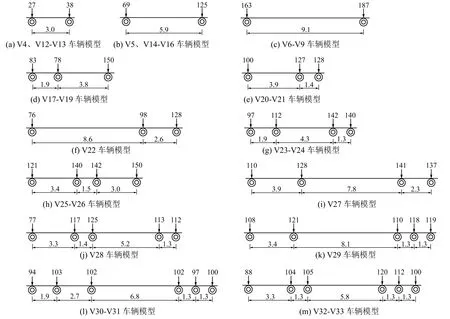
图3 典型车辆荷载模型Fig.3 Typical vehicle load model

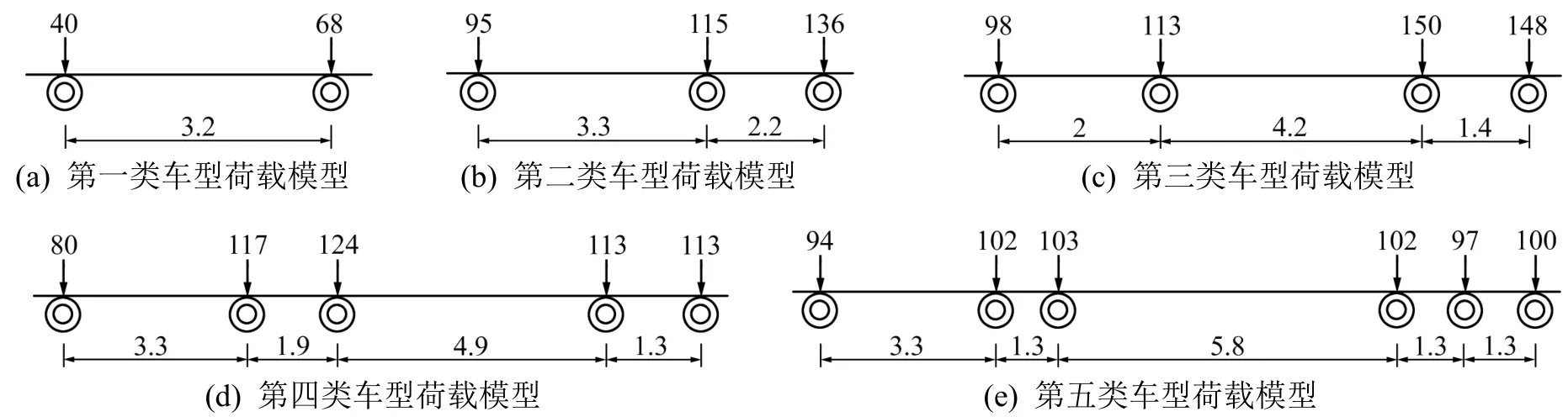
图4 专用车辆荷载模型Fig.4 Special vehicle load model

通过专用疲劳荷载谱计算出不同车型对桥梁结构的相对破坏能力[16]，进而找到对桥梁损害贡献率最大的车型，然后以该车型作为原型推导出标准车辆荷载谱。

根据S-N疲劳曲线幂函数方程，可认为变幅荷载所致疲劳损伤与常幅荷载所致疲劳损伤的S-N 曲线有相同的规律，即可定义损伤贡献率为：

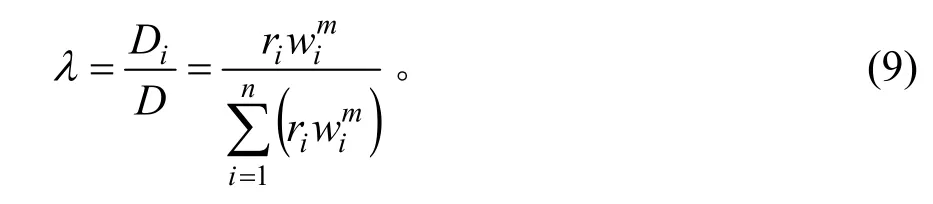
式中：Di为第i种车型对桥梁造成的损伤；D为不同车型对桥梁造成的损伤之和；ri为每类代表车型出现的频率；wi为第i种车型的等效车重。

由式(9)分别计算出5 类车的疲劳加载贡献率，计算结果见表4。

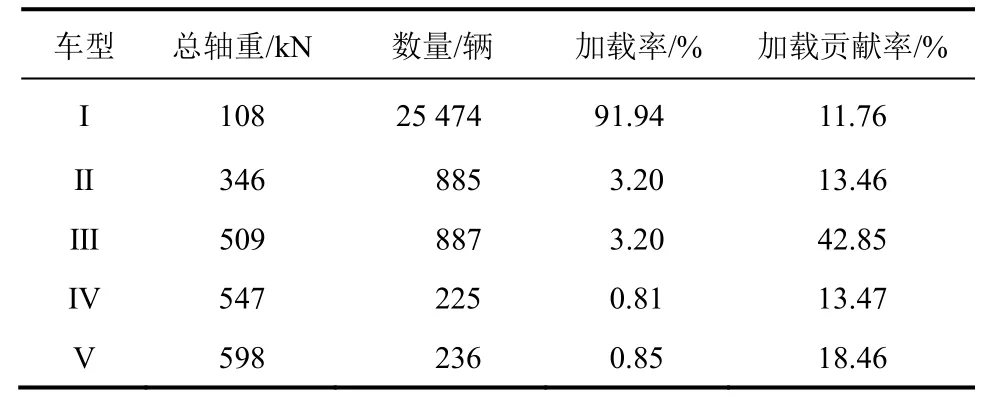
表4 疲劳加载贡献Table 4 Fatigue loading contributions

从表4 可以看出，加载贡献率主要受总轴重影响，车数影响不大。第三类车(总轴重509 kN)，加载贡献率最大，为42.85%，其次为第五类车(总轴重598 kN)，加载贡献率为18.46%；数量最多的第一类车(总轴重108 kN)，加载贡献率最小，仅为11.76%。采用加载贡献最大的第三类(四轴车)和第五类(六轴车)车型为云南省低等级公路的标准疲劳车[17]，两者的加载贡献值为61.31%。