湘府路高架桥桩基沉降计算及影响因素分析

2020-07-09胡超

交通科学与工程 2020年2期

胡超

(湖南湘江新区发展集团有限公司，湖南长沙 410205)

为了缓解城市交通车辆分流、提高城市交通容量及改善城市交通拥堵，在城市道路建设中，合理设置高架桥显得尤为重要。由于越来越多的高架桥修建在软弱土层或岩溶地区地层中，土层承载力不足，将导致桩基沉降增大，严重地危害了桥梁的安全[1-3]。近年来，已有一些学者对基桩沉降问题进行了相关的试验和理论研究。陈锦剑[4]等人根据300根单桩荷载试验结果，研究了软土地区单桩变形特性。张瑞坤[5]等人基于现场静荷载和桩身应力测试试验，利用一维杆系结构有限单元法与剪切位移法的耦合，分析了单桩沉降。成滢[6]等人建立了基桩受力分析的简化计算模型，得到了基桩内力与位移的挠曲微分方程及其幂级数解答。这些研究通过模型试验结果，从竖向承载角度来分析基桩的沉降变形和承载特性，但未考虑荷载施加过程中桩侧摩阻力和桩端阻力发挥程度。刘红军[7]等人基于荷载传递法的土弹簧模型，建立了用于单桩沉降计算的数学规划模型。靳建明[8]等人基于成层Gibson 地基模型，研究了轴向荷载作用下单桩的非线性沉降响应。刘忠[9]等人基于荷载传递法，采用描述桩-土相互作用特性的双折线荷载传递函数。已有的基桩承载特性和沉降的研究大多从试验和理论上分析了桩-土相互作用机理，研究嵌岩桩或摩擦桩的沉降特性和竖向承载性能。但现有的研究成果还不够完善，未体现基桩受荷过程中桩侧土非线性特征对基桩沉降的影响。因此，作者拟考虑桩侧土体应力-应变的非线性特征，分析竖向荷载作用下的桩-土相互作用的机理，建立双曲线模型，用荷载传递简化计算方法，推导基桩沉降的幂级数解，探讨桩径和桩长等参数对基桩沉降特性的影响，以期为桩基工程的设计提供参考。

1 计算基桩沉降的荷载传递法

由于荷载传递法能很好地拟合桩-土相互作用，在基桩沉降计算时被广泛采用。当竖向载荷施加于桩顶、桩身产生压缩与土体发生相对位移时，其位于基桩上部土层的桩侧摩阻力相较于下部土层先发挥出来，而桩侧阻力会比桩端阻力先发挥出来。因此，竖向荷载作用下桩土体系的传递荷载过程可看成是桩身沉降s(z)和桩身轴力Q(z)随深度逐渐递减，而桩侧摩阻力τ(z)发挥的过程，如图1 所示。

取桩身微端dz作为研究对象，由竖向受力平衡公式可得：

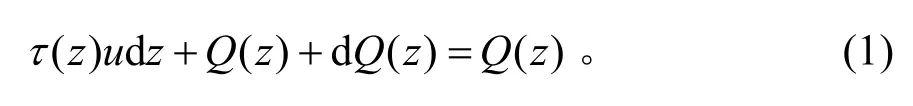
即：

任一深度z处桩身截面荷载为：

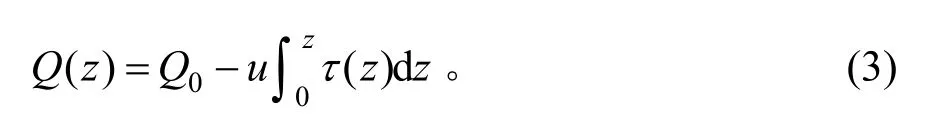
可得任一深度z处桩身位移为：

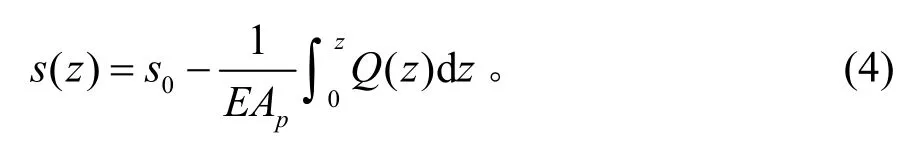
各微段dz压缩量与轴力的关系式为：

进一步可得桩身轴力表达式为：

联立式(2)和(6)，可得桩身控制方程为：

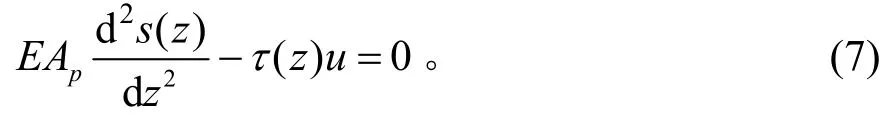
式中：z为基桩计算点深度；Ap为桩身截面面积；u为桩身周长；E为桩身混凝土弹性模量。

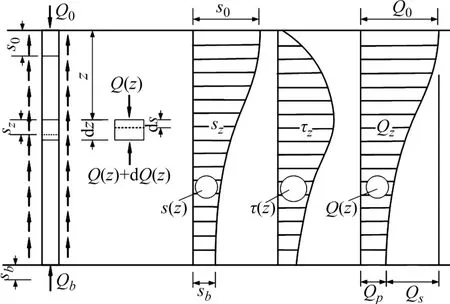
图1 基桩荷载传递模型Fig.1 Load transfer model of foundation pile

由于双曲线模型能较好地模拟桩侧土体的应力-应变非线性关系，因此，可采用双曲线模型作为求解基桩荷载传递基本方程。

关于桩侧土体的应力-应变关系，Kraft[10]等人考虑土的应力-应变的非线性特征，提出了相应的双曲线模型，其表达式为：

式中：s为桩土相对位移；a,b均为待定系数，其物理意义如图2 所示。

将传递函数双曲线模型式(8)代入式(7)，可得：

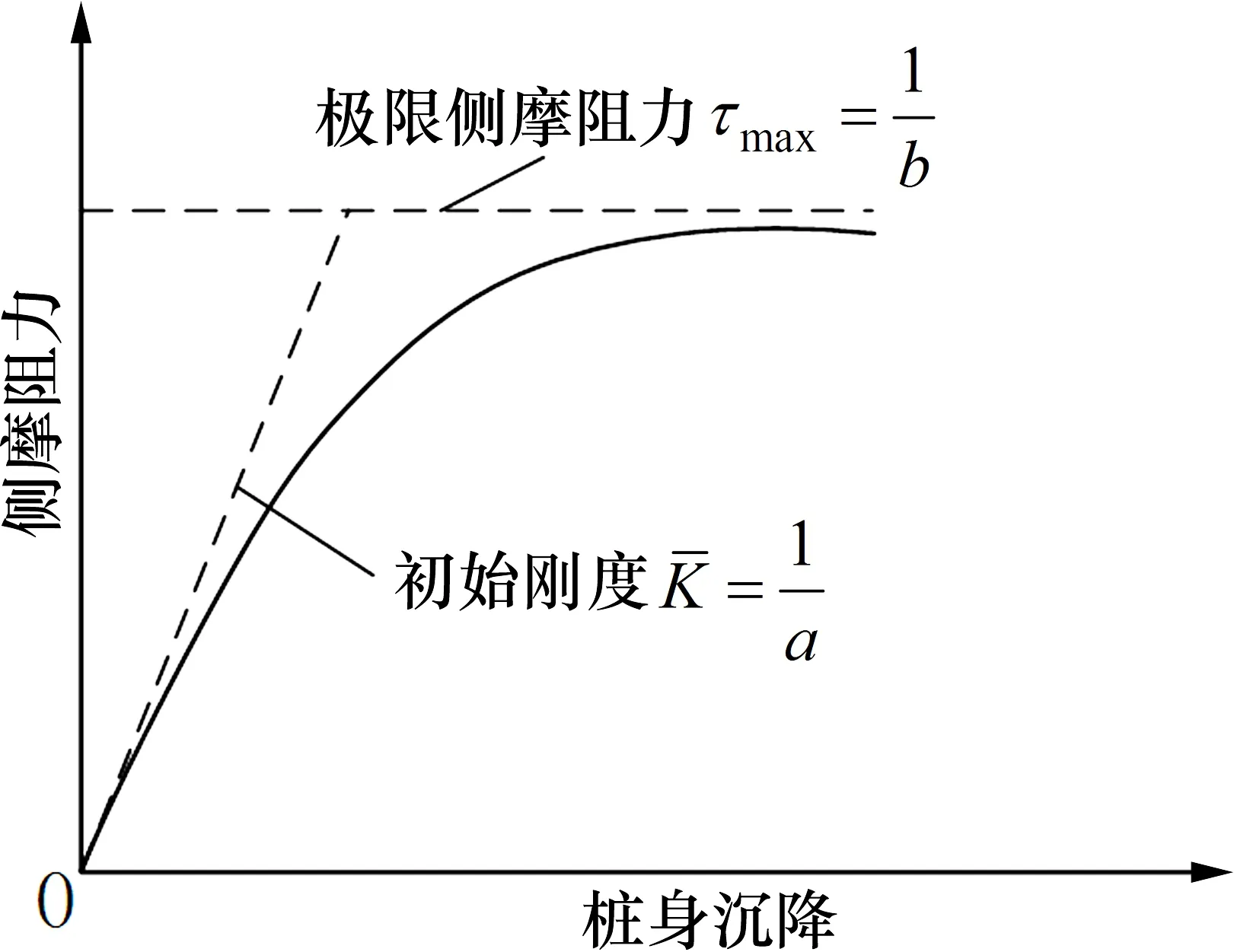
图2 双曲线模型Fig.2 Hyperbolic model

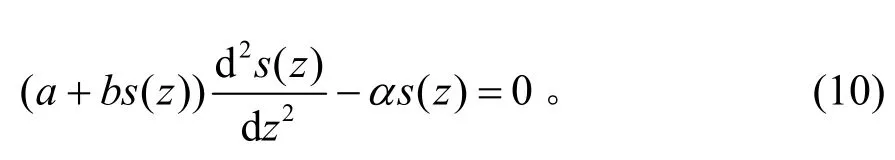
假设桩身沉降函数为：

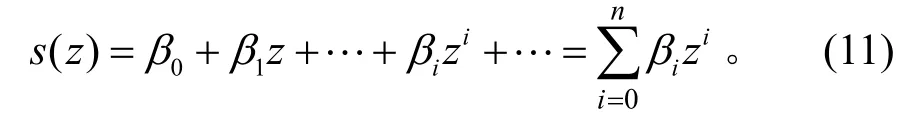
式中：βi为沉降方程展开系数。

桩顶边界条件为：

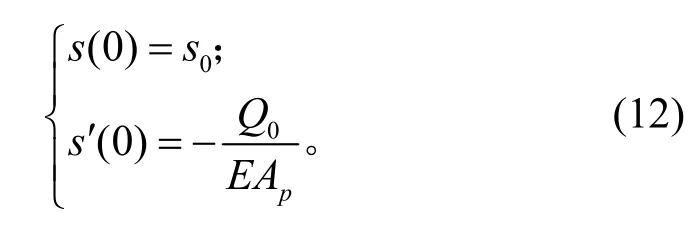
通过求解，得到计算系数的递推关系为：

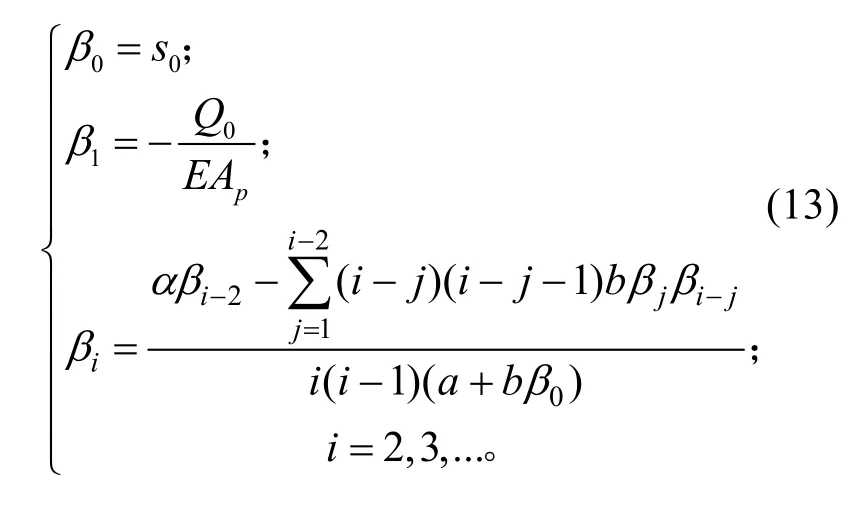
这一求解过程可编制相应的计算程序来实现。

2 桥墩基桩沉降的计算

2.1 工程概况

在湘府路(河西段)快速化改造工程中，ZX48～ZX51 墩台位于主线高架桥梁落地位置，东接湘府路大桥西侧路基挡墙段。ZX48～ZX51 联采用变高变宽连续梁，其中，ZX49R 墩为该联中墩，上部结构为预应力砼变高变宽连续箱梁。由该墩地质勘查资料显示，ZX49R 墩周覆盖层由填筑土、粉质黏土及圆砾等组成，其承载力较低，不宜做基础持力层(各地层参数见表1)。ZX49R 墩存在稳定持力岩层或埋深极深的情况，局部揭露岩层存在溶洞，不具备嵌岩桩设计的地质条件，故将ZX49R墩的基桩设计为摩擦桩，如图3 所示。

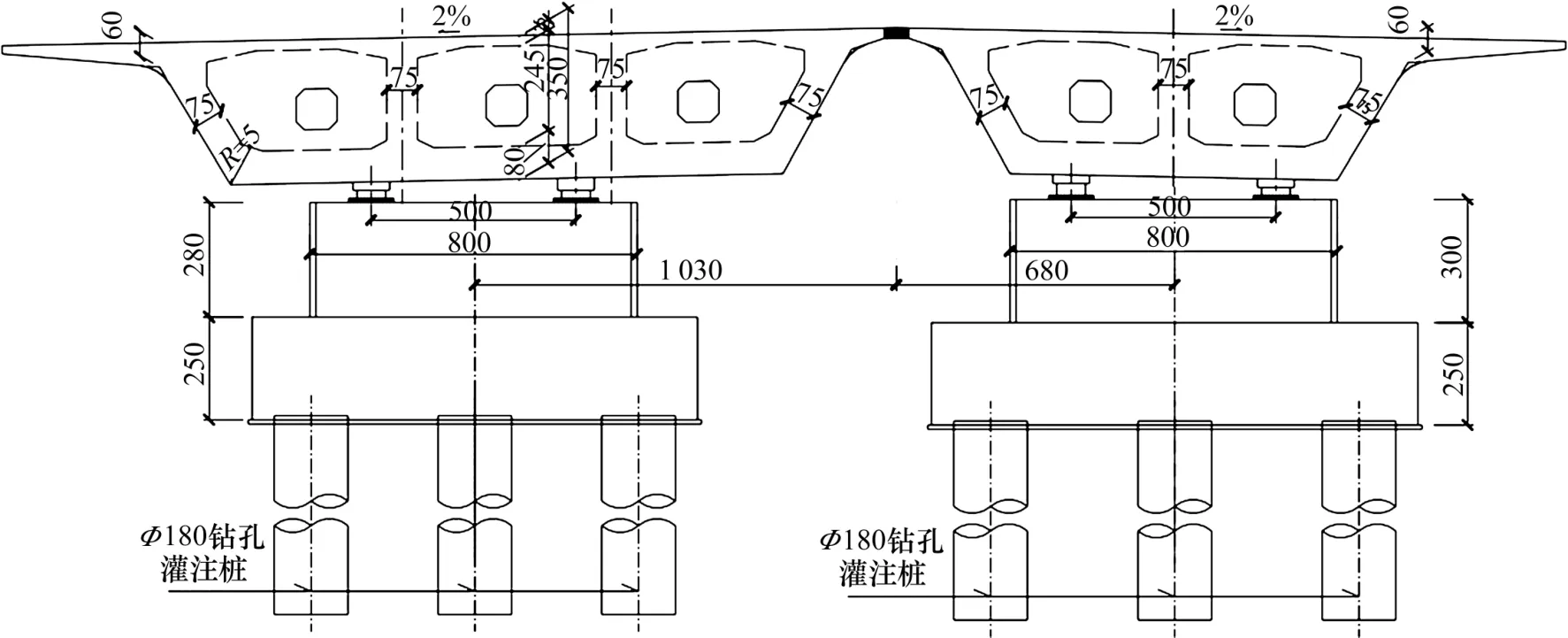
图3 ZX49R 墩桩基布置(单位：cm)Fig.3 Layout of the ZX49R pile foundation (unit: cm)

2.2 基桩沉降计算

ZX49R 墩基桩为钻孔灌注桩，桩径D=1.8 m；基桩总长L=44.0 m。桩侧土层自上而下依次为粉质黏土、圆砾和微风化灰质白云岩，如图4 所示。

基桩参数为：混凝土的弹性模量Ec为30.0 GPa，抗弯刚度EI为15.5 GN·m2。粉质黏土含水量w为25.0%，容重γ1为18.0 kN/m3，黏聚力c为10.0 kPa，内摩擦角φ为15.0°，压缩模量Es为6.0 MPa，摩阻力标准值q1k为60.0 kPa。圆砾的容重γ2为23.0 kN/m3，变形模量E0为23.0 MPa，摩阻力标准值q2k为130.0 kPa。微风化灰质白云岩单桩抗压强度标准值frk为40.0 MPa。计算得到的桩顶曲线如图5 所示。

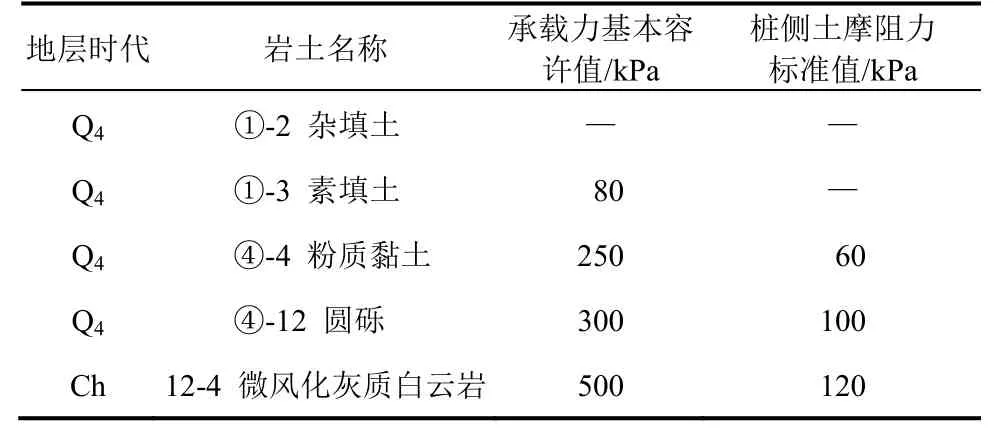
表1 地层力学指标推荐值Table 1 Recommended values for formation mechanics indexes

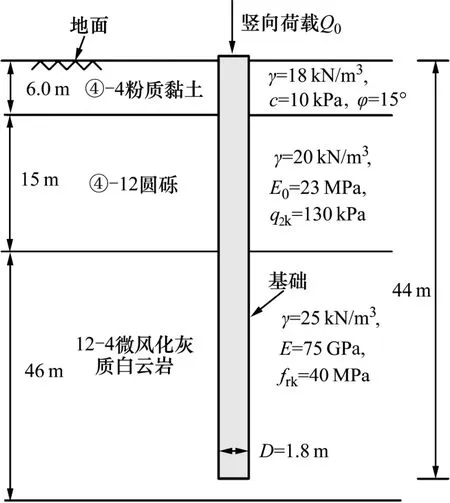
图4 ZX49 墩基桩计算示意Fig.4 Layout diagram of ZX49 pier foundation pile

从图5 中可以看出，实测荷载与沉降曲线和计算荷载与沉降曲线吻合较好，计算误差范围为-13.5%～3.9%，表明基桩沉降计算的荷载传递法是合理可行。实际工程中，由于基桩荷载不大，基桩荷载与沉降曲线近似呈线性增大趋势。

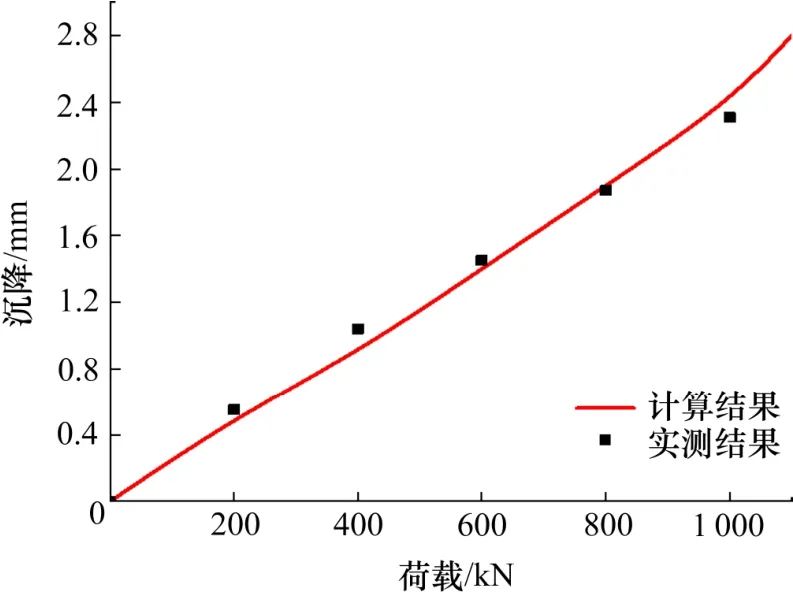
图5 桩顶荷载与沉降曲线Fig.5 The curve of the load and the settlement on the pile top

3 影响因素分析

桩径和桩长是影响竖向荷载作用下基桩沉降的主要因素。在不同桩径和桩长条件下，对桩顶沉降的变化规律展开影响因素及其敏感性分析。敏感性分析方法分为单因素敏感性分析法和多因素敏感性分析法[11]。本试验采用单因素敏感性分析法对该墩的基桩进行分析，即在保持其他参数条件不变的情况下，以桩径D=1.8 m 和桩长L=39 m 为基准，分别探讨D和L增(减)10%,20%和30%对基桩沉降的影响程度。

3.1 桩径的影响

以实际工程中D=1.8 m 为基准，桩径分别减(增)10%,20%和30%，对应的D分别为1.2,1.4,1.6,2.0,2.2 和2.4 m。经计算，得到不同D下的桩顶荷载与沉降曲线，如图6 所示。当竖向荷载Q=10 000 kN时，桩顶沉降s增量与桩径增量ΔD之间的敏感性关系见表2。

从图6 中可以看出，桩顶沉降随D的增大呈非线性减小趋势，随桩顶竖向荷载Q增加而呈非线性增大趋势。以实际D=1.8 m 为例，当Q0为2 000,6 000,10 000,14 000 和18 000 kN时，s分别为5.3,15.1,26.5,41.1 和59.4 mm，与前一荷载对比，其增幅分别为184.9%,75.5%, 55.1%和44.5%。从表2 中可以看出，当D在±30%范围内变化时，桩顶沉降变化幅度介于-4.91%～ 23.40%之间。可见，增大桩径对于减小基桩沉降具有显著效果，但当其增大到一定程度后，继续增大桩径对改善基桩沉降的效果已不明显。

图6 桩径的影响Fig.6 The effects of pile diameter

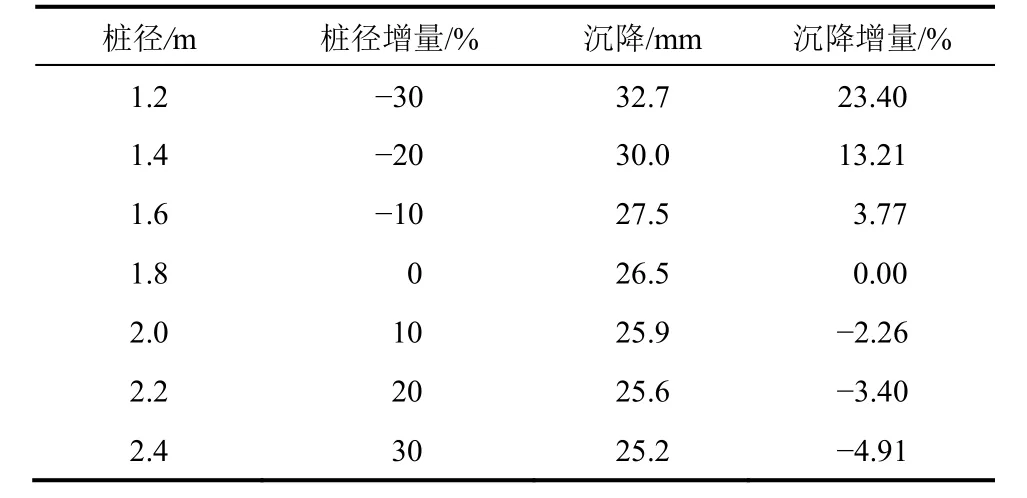
表2 桩径的敏感性分析Table 2 Sensitivity analysis of pile diameter

3.2 桩长的影响

以实际工程中的L=39 m 为基准，L分别减(增)10%,20%和30%，对应的L分别为27,31,35,43,47和51 m 经计算，得到不同桩长条件下的桩顶荷载与沉降曲线，如图7 所示。当Q=10 000 kN 时，桩顶沉降s增量与桩长增量ΔL之间的敏感性关系见表3。

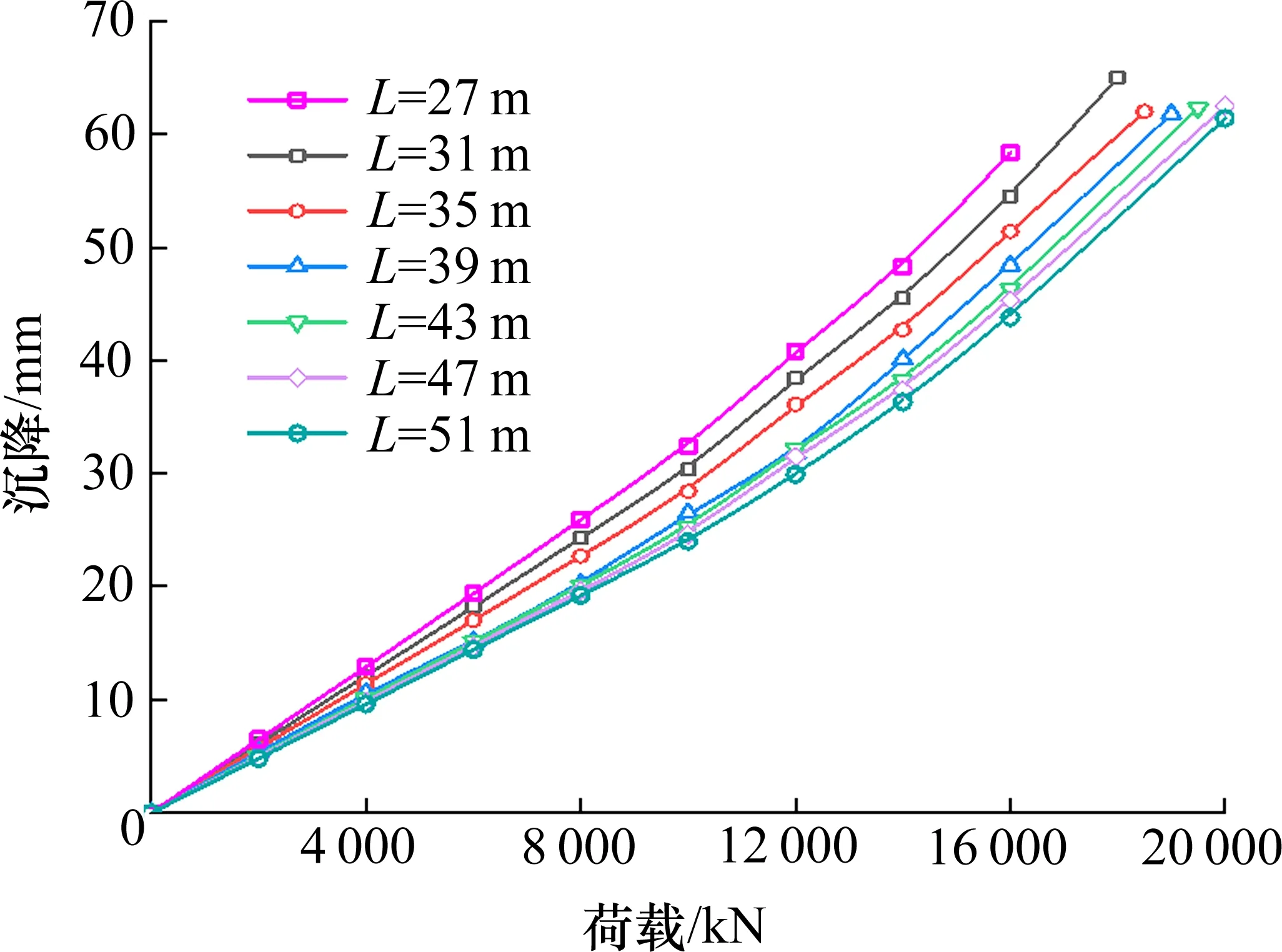
图7 桩长的影响Fig.7 The effects of pile length

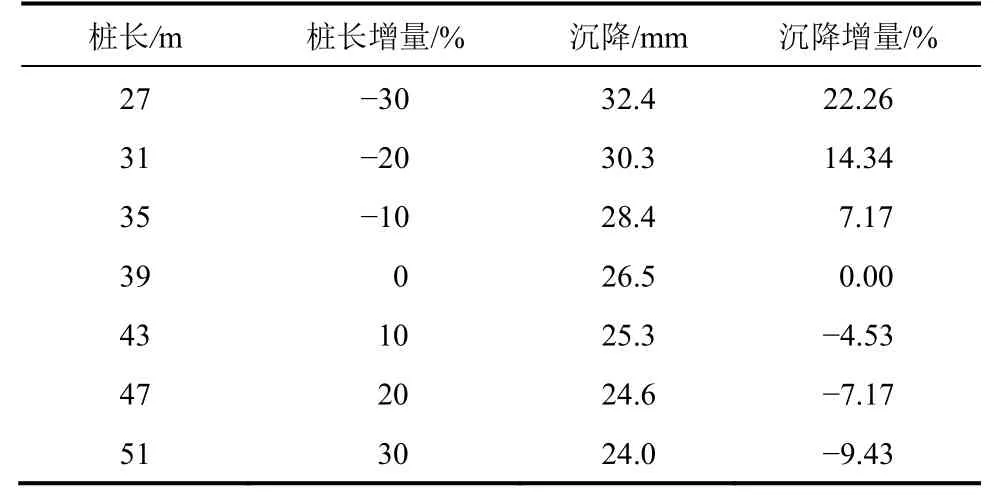
表3 桩长的敏感性分析Table 3 Sensitivity analysis of pile length

从图7 中可以看出，桩顶沉降随L的增大呈非线性减小趋势，随Q增加而呈非线性增大趋势。以桩长L=43 m 为例，当Q0为2 000, 6 000,10 000,14 000 和 18 000 kN 时，桩顶沉降s分别为5.0,15.1,25.2,38.2 和55.4 mm，与前一荷载对比，其增幅分别为202.0%,66.9%,51.6%和45.0%。从表3中可以看出，当D在±30%范围内变化时，桩顶沉降变化幅度介于-9.43%～22.26%之间。以Q为10 000 kN 为例，当L减小20%时，桩顶沉降约减小14.34%；而当L增大20%时，桩顶沉降约增加7.17%。表明：增大L对于减小基桩沉降作用明显。但随着L增大到一定程度后，桩长已不再是控制桩顶沉降的关键参数。

增大桩径和桩长均能减小基桩沉降，且基桩荷载与沉降曲线变化趋势相近，两者对基桩竖向受荷沉降的敏感性相差不大。