融合唤醒阈值与半休眠模式的云虚拟机调度策略
2020-07-09李吉良李文江金顺福王志斌
李吉良,秦 兵,李文江,金顺福,王志斌
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.通信网信息传输与分发技术国家重点实验室,河北 石家庄 050081;3.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;4.燕山大学 电气工程学院,河北 秦皇岛 066004)
0 引言
在云平台中,云服务提供商负责管理和分配云上的所有数据与资源,用户则按需获取资源。毫无疑问,这些资源对于用户和云提供商来说,是非常重要的资产。平衡云用户与云提供商两者利益的关键在于合理分配云资源[1-2]。越来越多的研究专注于以降低云计算数据中心能耗和提高系统资源利用率为目标的云计算资源管理。
Saikrishna等[3]将Web服务器看成一个含有两种控制输入(虚拟机个数和工作量)的可变容量系统,针对系统控制输入频繁改变的问题,建立了一个多输入多输出的线性变参数(Linear Parameter-Varying,LPV)系统,设计了一种增益调度线性二次型调节控制器用于保证性能。Paya等[4]提出了一种应用于云负载均衡与云应用扩展的能量感知操作模型,通过最大化运行服务器的工作负载,将空闲和低负载的服务器转换为休眠状态,达到节能的目的。Singh等[5]提出了一个能量高效的自优化云计算系统,用于数据中心云资源的高效调度,将能量视为服务质量参数,通过降低能量消耗优化云资源的使用。
以上研究只是考虑了云计算的能量节省而忽略了响应性能的要求。本文综合云平台上的能量消耗和云用户请求的响应性能,将唤醒阈值与半休眠模式相结合,提出一种新型的云虚拟机调度策略。将云平台上的虚拟机与云用户请求抽象为服务台和顾客,构造一个带有策略和多重异步工作休假的多服务台排队系统。结合虚拟机状态和云用户请求数量,构造二维连续时间马尔科夫(Markov)链,采用矩阵几何解方法,推导系统节能率与云请求平均逗留时间的表达式,评估云虚拟机调度策略的系统性能。按照云虚拟机调度策略的工作原理进行仿真实验,得到相对应的性能指标的统计结果。比较数值分析结果和仿真实验的统计结果,验证所提策略的可行性及模型解析的正确性。综合不同的性能指标建立成本函数,利用蚁群智能寻优算法,得到使系统成本最小的唤醒阈值与半休眠参数,进而给出云虚拟机调度策略的优化方案。
1 云虚拟机调度策略及系统模型
1.1 云虚拟机调度策略
在传统的云平台中,即便没有任何云用户请求,虚拟机仍要以正常速率运行,从而增加了能量消耗。
置空闲的虚拟机于休眠模式,可以有效降低系统的能耗水平,但云用户请求的响应性能将受很大影响。半休眠机制是指虚拟机在休眠期间以较低的速率为云用户请求提供服务,而不是完全停止服务。引入半休眠机制实质是使系统中的虚拟机以两种不同服务速率交替运行,以解决节能水平与响应性能之间的矛盾。
为了减少速率转换带来的额外耗能,在半休眠模式中引入唤醒阈值N。只有当云缓冲区中的云用户请求数量大于或等于唤醒阈值N时,虚拟机才可能从半休眠阶段进入唤醒阶段,以正常速率为云用户请求提供服务。基于此,提出一种融合唤醒阈值与半休眠模式的云虚拟机调度策略。策略中唤醒阈值N与虚拟机的数量c一定满足N≥c。
将云平台中虚拟机状态分为低速空闲、低速工作与正常工作,描述云虚拟机调度策略如下。
1) 当虚拟机以正常速率完成一个云用户请求的服务时,如果云缓冲区中没有其他云用户请求排队等待,虚拟机将进入半休眠阶段,启动半休眠定时器,开始一次新的半休眠周期,虚拟机由正常工作状态转换为低速空闲状态;否则,虚拟机将继续以正常速率为云缓冲区中排队等待的第一个云用户请求提供服务,即保持在正常工作状态。
2) 处于低速空闲状态的虚拟机可以立即为新到达的云用户请求提供服务,虚拟机由低速空闲状态转换为低速工作状态。当虚拟机处于低速空闲状态时,如果半休眠定时器到期,虚拟机将重新启动半休眠定时器,开始一次新的半休眠周期,即保持在低速空闲状态。
3) 当虚拟机以低速率完成一个云用户请求的服务时,如果云缓冲区中没有其他云用户请求排队等待,虚拟机由低速工作状态转换为低速空闲状态;否则,虚拟机将继续以低速率为云缓冲区中排队等待的第一个云用户请求提供服务,即保持在低速工作状态。
4) 处于低速工作状态的虚拟机在半休眠定时器到期时,统计云缓冲区中排队等待的云用户请求数量。如果云缓冲区中排队等待的云用户请求数量大于或等于唤醒阈值时,虚拟机将进入唤醒阶段,以正常速率为未完成的云用户请求持续提供服务,虚拟机由低速工作状态转换为正常工作状态;否则,虚拟机将重新启动半休眠定时器,开始一次新的半休眠周期,继续以低速率为未完成的云用户请求提供服务,即保持在低速工作状态。
1.2 系统模型
考虑云平台上的一台物理机。假设在这台物理机上部署多个虚拟机,称之为虚拟机集群。将半休眠模式抽象成工作休假,每个半休眠周期为一次工作休假;将虚拟机和云用户请求分别抽象成服务台和顾客。根据所提出的云虚拟机调度策略的工作原理,建立一个带有N策略和多重异步工作休假的连续时间排队模型。
假设云用户请求的到达时间间隔服从参数为λ的指数分布。假设处于正常工作状态的虚拟机服务一个云用户请求的时间服从参数为μh(μh>0)的指数分布,处于低速工作状态的虚拟机服务一个云用户请求的时间服从参数为μl(μl>0)的指数分布,且μh>μl。假设一次半休眠过程的时间长度服从参数为的θ(θ>0)指数分布,称θ为半休眠参数。当一次半休眠结束时,如果云缓冲区中的云用户请求数量大于或等于唤醒阈值N,虚拟机立即停止半休眠,服务率由μl提高至μh,此时云用户请求将以正常速率继续接受服务;否则,虚拟机重新开始一次独立同分布的半休眠过程。基于以上假设,得出系统的稳态条件为λ 令L(t)表示t时刻云用户请求的数量,J(t)表示t时刻处于正常工作状态的虚拟机数量。{L(t)=k,J(t)=j,t≥0}表示系统的状态,其状态空间为 Ω={(k,j)|k∈{0,1,2,…}, j∈{0,1,2,…,c}}。 {L(t)=k,J(t)=j,t≥0}构成一个二维连续时间Markov链[6]。假设{L(t)=k,J(t)=j,t≥0}正常返,令πkj表示二维连续时间Markov链的稳态分布。πkj定义为 πkj=limP{L(t)=k,J(t)=j},(k,j)∈Ω。 令πk(k≥0)表示在稳定状态下系统水平的概率分布,则 πk=(πk0,πk1,πk2,…,πkc),k≥0 Π=(π0,π1,π2,…)。 在Markov链的状态转移过程中,第n次结果只受第n-1次的结果的影响。故根据一步转移原则,系统状态变化分析如下: 1) 系统中云用户请求数量由k(k>0)变为k-1,说明有一个云用户请求离开系统。 当0 当1 当0 当k>c且j≤c时,系统中有(c-j)个虚拟机低速率工作,有j个虚拟机正常速率工作。云用户请求无论是由低速率工作的虚拟机完成,还是由正常速率工作的虚拟机完成,系统状态都由(k,j)转移到(k-1,j),转移率为(c-j)μl+μh。 2) 系统中的云用户请求数量保持在k(k≥0),说明既没有云用户请求离开也没有云用户请求到达。 当0 当1 当0 当k>c且j≤c时,系统中有(c-j)个虚拟机低速率工作,有j个虚拟机正常速率工作。系统状态保持不变的转移率为-(λ+(c-j)μl+jμh)。 当k≥c+N且j≤c时,系统中的虚拟机有(c-j)个低速率工作,有j个正常速率工作。如果某个低速率工作的虚拟机半休眠定时器到期,该虚拟机进入唤醒阶段,系统状态由(k,j)转移到(k,j+1),转移率为(c-j)θ;否则,系统状态保持不变,转移率为-(λ+(c-j)μl+jμh+(c-j)θ)。 3) 系统中的云用户请求数量由k(k≥0)变为k+1,说明有一个云用户请求到达系统。 当新的云用户请求的到达系统时,系统状态由(k,j)转移到(k+1,j),转移率为λ。 令Q表示二维连续时间Markov链的一步转移率矩阵。根据状态转移过程,在任意时刻,系统中的云用户请求数量只能减少一个、固定不变或增加一个,即转移只能发生在相邻状态。 1) 系统中的云用户请求数量减少一个。 当1≤k≤c时,子块Bk是一个(k+1)×k的非负矩阵,Bk表示为 k-1,0k-1,1k-1,2…k-1,k-1 (1) 当k>c时,子块Bk是一个c+1阶方阵,Bk表示为 k-1,0k-1,1 …k-1,c-1k-1,c (2) 2) 系统中的云用户请求数量固定不变。 当k=0时,子块A0退化为一个数值,表示为 A0=-λ。 (3) 当1≤k≤c时,子块Ak是一个k+1阶含负对角线元素的方阵,Ak表示为 k,0k,1…k,k-1k,k 其中,αx=-(λ+(x-1)μh+(k-x+1)μl),1≤x≤k+1。 当c k,0k,1…k,c-1k,c (5) 其中,βy=-(λ+(y-1)μh+(c-y+1)μl),1≤y≤c+1。 当k≥c+N时,子块Ak是一个c+1阶方阵,Ak表示为 k,0k,1k,2…k,c (6) 其中,φz=-(λ+(c-z+1)μl+(z-1)μh+(c-z+1)θ),1≤z≤c+1。 3) 系统中的云用户请求数量增加一个。 当k=0时,子块C0退化为一个数值,表示为 C0=λ。 (7) 当1≤k≤c时,子块Ck是一个(k+1)×(k+2)阶矩阵,Ck表示为 k-1,0k-1,1…k-1,k-1k-1,kk-1,k+1 (8) 当k≥c时,子块Ck是一个c+1阶方阵,Ck表示为 Ck=λI, (9) 其中,I是c+1阶单位矩阵。 由上述子块的表示形式可知,当k≥c+N时,子块Bk,Ak,Ck中的元素不再变化。将重复的子块Bk,Ak,Ck(k≥c+N)分别记作B,A,C。子块B,A,C分别表示为 (10) (11) 其中,ξp=-(λ+(c-p+1)μl+(p-1)μh+(c-p+1)θ),1≤p≤c+1。 C=λI, (12) 其中,I是c+1阶单位矩阵。 综合以上分析,给出二维连续时间Markov链的一步转移率矩阵令Q为 由矩阵Q的结构可知,二维连续时间Markov链{L(t),J(t),t≥0}是一个拟生灭过程(QBD)[7-8]。QBD正常返的充分必要条件是矩阵二次方程R2B+RA+C=0的最小非负解R的谱半径SP(R)<1。由式(10)~(12)可知,B,A,C都是上三角形式的矩阵,可知率阵R必然也是上三角形式的。设 (13) 将R,B,A,C代入矩阵二次方程得到矩阵R。 由矩阵几何解方法[9-10]可得ΠB[R]=0,其中 (14) 二维连续时间Markov链的平稳分布满足 (15) 其中,e1是(C+N)×(c+1)列全1向量,e2是c+1列全1向量,I是c+1阶单位矩阵。 通过式(15)可以给出系统稳态分布πk(k≥0)的数值解。 基于系统模型的稳态解,分析融合唤醒阈值与半休眠模式的云虚拟机调度策略的性能指标。 1) 定义云用户请求平均逗留时间W为一个云用户请求从进入系统开始到离开系统时刻所经历的平均时间长度(包括在云缓冲区中的等待时间与在虚拟机上接受服务的时间)。云用户请求平均逗留时间是衡量系统中云用户请求服务质量的重要指标。由Little公式[11]可知,云用户请求平均逗留时间W表达式为 (16) 2) 定义系统节能率φ为单位时间内因设置唤醒阈值与半休眠模式而节省的能量消耗。系统节能率是衡量云平台上节能策略有效性的重要指标。在所提出的云虚拟机调度策略中,在半休眠阶段,假设处于工作状态的虚拟机单位时间消耗能量为ωlb,处于空闲状态的虚拟机单位时间消耗能量为ωli;在唤醒阶段,假设处于工作状态和空闲状态的虚拟机单位时间消耗能量分别为ωhb和ωhi;将单位时间内虚拟机由半休眠阶段转入唤醒阶段时所消耗的能量记为ωt。系统节能率φ表达式如下: φ=(ωhi-ωliμl)·Nidle+(ωhb-ωlbμl) (17) 为了验证融合唤醒阈值与半休眠模式的云虚拟机调度策略的有效性,并进一步分析系统参数对系统性能的影响,进行数值与仿真实验,定量刻画云用户请求平均逗留时间与系统节能率的变化趋势。系统实验的运行环境:MATLAB R2011a,Eclipse,Intel Core i7-4790 CPU @ 3.60 GHz,8.00GB RAM。数值分析实验在MATLAB环境下运行,仿真实验在Eclipse环境下使用Java语言运行。 在保证系统平稳的前提下,参数的具体取值不会影响系统性能指标的变化趋势。本文的实验参数设置如下:系统中虚拟机数量c=10台,云用户请求到达率λ=5.0 s-1,正常工作服务率μh=2.0 s-1,处于唤醒阶段空闲虚拟机的能量消耗ωhi=0.55 mW,处于唤醒阶段工作虚拟机的能量消耗ωhb=0.62 mW,处于半休眠阶段空闲虚拟机的能量消耗ωli=0.5 mW,处于半休眠阶段工作虚拟机的能量消耗ωlb=0.6 mW,由半休眠阶段切换到唤醒阶段虚拟机的能量消耗ωt=2.5 mJ。 针对不同的唤醒阈值N与不同的虚拟机低速服务率μl,云用户请求平均逗留时间W随半休眠参数θ的变化趋势如图1所示。 图1 云用户请求平均逗留时间的变化趋势 对比图1(a)与(b)可知,当虚拟机低速服务率μl与半休眠参数θ一定时,随着唤醒阈值N的增大,云用户请求平均逗留时间W增加。当唤醒阈值较大时,虚拟机处于半休眠阶段的时间延长,更多的云用户请求被低速工作的虚拟机处理,虚拟机处理云用户请求的时间延长,因此云用户请求平均逗留时间增加。 分别观察图1中的(a)与(b)可知,当唤醒阈值N与半休眠参数θ一定时,随着低速服务率μl的增大,云用户请求平均逗留时间W减少。当低速服务率较大时,低速工作的虚拟机处理云用户请求的时间缩短,因此云用户请求平均逗留时间减少。 由图1中的(a)与(b)可知,当唤醒阈值N与低速服务率μl一定时,随着半休眠参数θ的增大,云用户请求平均逗留时间W减少。在等待的云用户请求数量达到唤醒阈值的情况下,当半休眠参数较大时,低速工作的虚拟机将更早地切换到正常工作状态。正常工作的虚拟机将以更快的速度处理云用户请求,因此云用户请求平均逗留时间减少。 针对不同的唤醒阈值N与不同的虚拟机低速服务率μl,系统节能率φ随半休眠参数θ的变化趋势如图2所示。 图2 系统节能率的变化趋势 对比图2中的(a)与(b)可知,当虚拟机低速服务率μl与半休眠参数θ一定时,随着唤醒阈值N的增大,系统节能率φ增加。当唤醒阈值较大时,虚拟机处于半休眠阶段的时间延长,虚拟机在半休眠阶段所消耗的能量较小,故系统节能率增加。 分别观察图2中的(a)与(b)可知,当唤醒阈值N与半休眠参数θ一定时,随着低速服务率μl的增大,系统节能率φ降低。当低速服务率提高时,虚拟机所消耗的能量随之增加,故系统节能率降低。 由图2中的(a)与(b)可知,当唤醒阈值N与低速服务率μl一定时,随着半休眠参数θ的增大,系统节能率φ降低。当半休眠参数较大时,低速工作的虚拟机将更早地切换到正常工作状态,正常工作的虚拟机所消耗的能量较大,故系统节能率降低。 以上的实验结果表明,云平台上的唤醒阈值N,低速服务率μl,半休眠参数θ对系统性能有着不容忽视的影响。唤醒阈值的加大使得云用户请求平均逗留时间与系统节能率均增加;低速服务率的提高使得云用户请求平均逗留时间与系统节能率均减小;半休眠参数的增大使得云用户请求平均逗留时间与系统节能率均减小。综上可知,不同参数对系统性能有着折中影响。为了能够更合理地满足云用户响应要求与最大限度地提高云平台能量效率,需要对唤醒阈值与半休眠参数进行联合优化。 为了平衡云用户请求平均逗留时间与系统节能率之间的折中关系,构造系统成本函数F为 F=fWW2-fφφ, (18) 其中,fW为云用户请求二次逗留时间影响因子,fφ为系统节能率影响因子。云用户请求平均逗留时间W由式(16)给出,系统节能率φ由式(17)给出。 沿用第4章给出的系统参数,并以fW=3.0,fφ=0.8为例,针对不同的低速服务率μl,进行系统实验,揭示唤醒阈值N与半休眠参数θ对系统成本函数F的影响。实验结果如图3所示。 图3 系统成本函数的变化趋势 观察图3可知,对于一定的低速服务率μl来说,适当地选取唤醒阈值N与半休眠参数θ,可以最小化成本函数F。针对每一个可选唤醒阈值,利用蚁群智能寻优算法找出最优半休眠参数θ以及最小成本。结合所选定的唤醒阈值及与唤醒阈值相关的最优半休眠参数,构造可选二元组(N,θ)。在全部的可选二元组中,进一步选取最小成本函数F*所对应的二元组,即唤醒阈值与半休眠参数最优组合(N*,θ*)。寻优结果如表1所示。 表1 唤醒阈值与半休眠参数的联合优化结果 低速服务率μl/s-1唤醒阈值与半休眠参数最优组合(N*,θ*)最小成本函数F*0.85(3,0.986 1)3.333 10.90(4,1.082 7)3.078 50.95(4,0.584 8)2.890 51.00(5,0.573 7)2.761 4 融合唤醒阈值与半休眠模式提出了一种最小化云平台成本的云虚拟机调度策略。唤醒阈值的引入可以提高云平台的节能效率;半休眠模式的引入可以满足云用户请求的响应要求。综合云平台上云用户请求数量与以正常速率服务的虚拟机数量,建立二维连续时间Markov链,利用矩阵几何解方法,给出了系统性能指标的表达式。分别采用MATLAB与Eclipse进行数值分析与系统仿真实验,实验结果表明,适当地选取唤醒阈值与半休眠参数,可以使所提出的云虚拟机调度策略在保证云用户请求响应性能的同时提高云平台节能效率。折中云用户请求平均逗留时间与系统节能率,构造成本函数,进行策略参数的联合优化,实现了系统成本的最小化。2 模型解析
2.1 状态转移过程
2.2 平稳分布
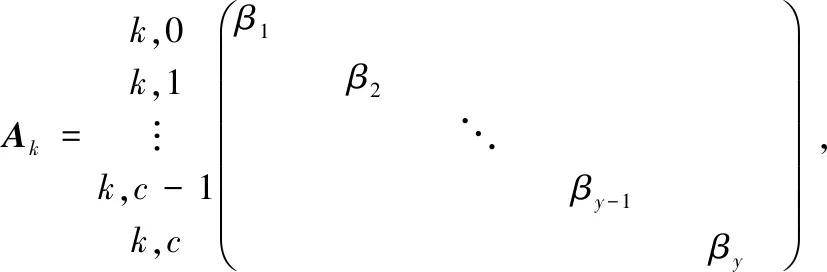

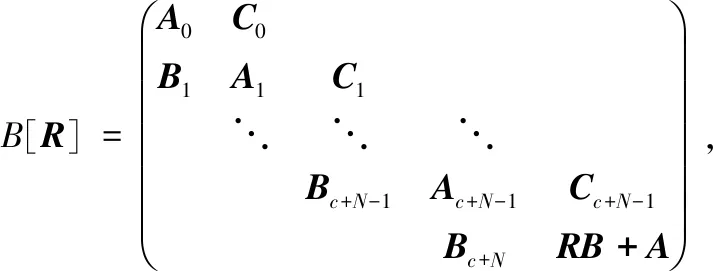
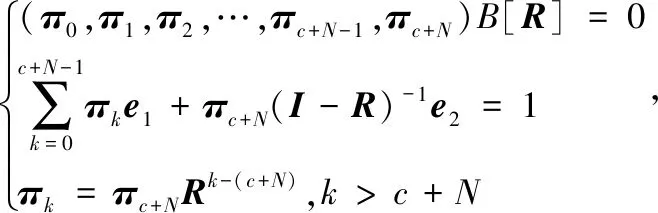
3 系统性能指标
Nbusy-ωtNtransterθ,
4 数值与仿真实验


Fig.1 Cloud users request an average trend of stay time
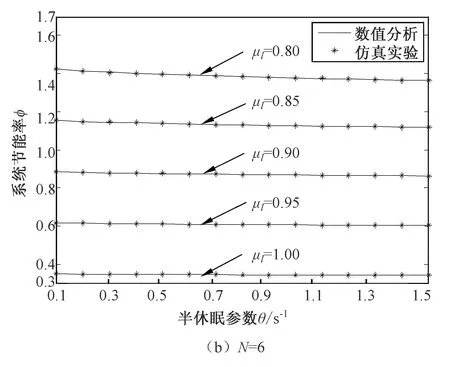
Fig.2 Trend of system energy saving rate5 系统优化
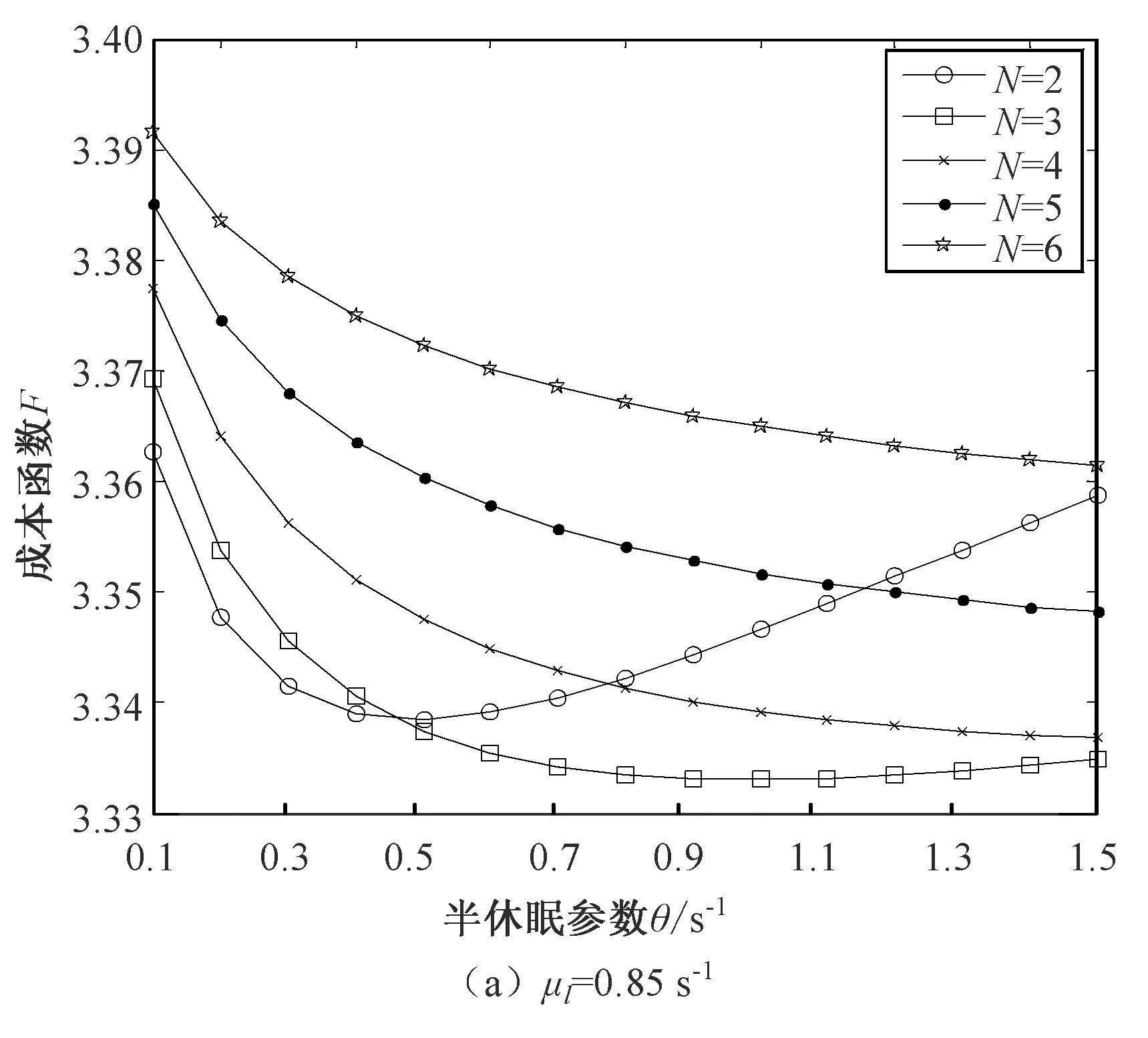
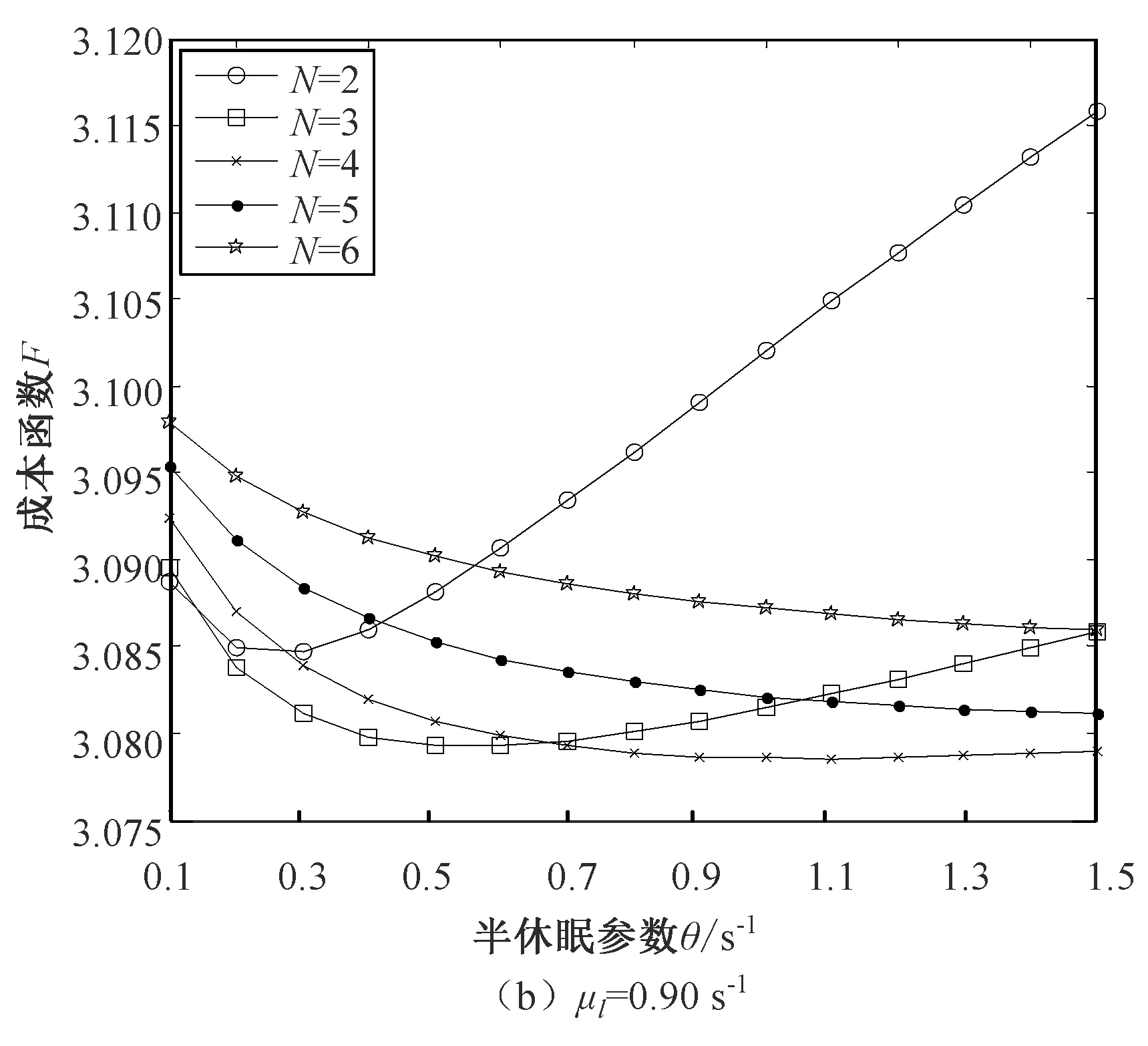
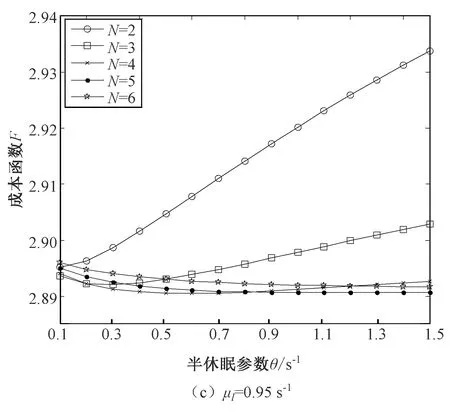
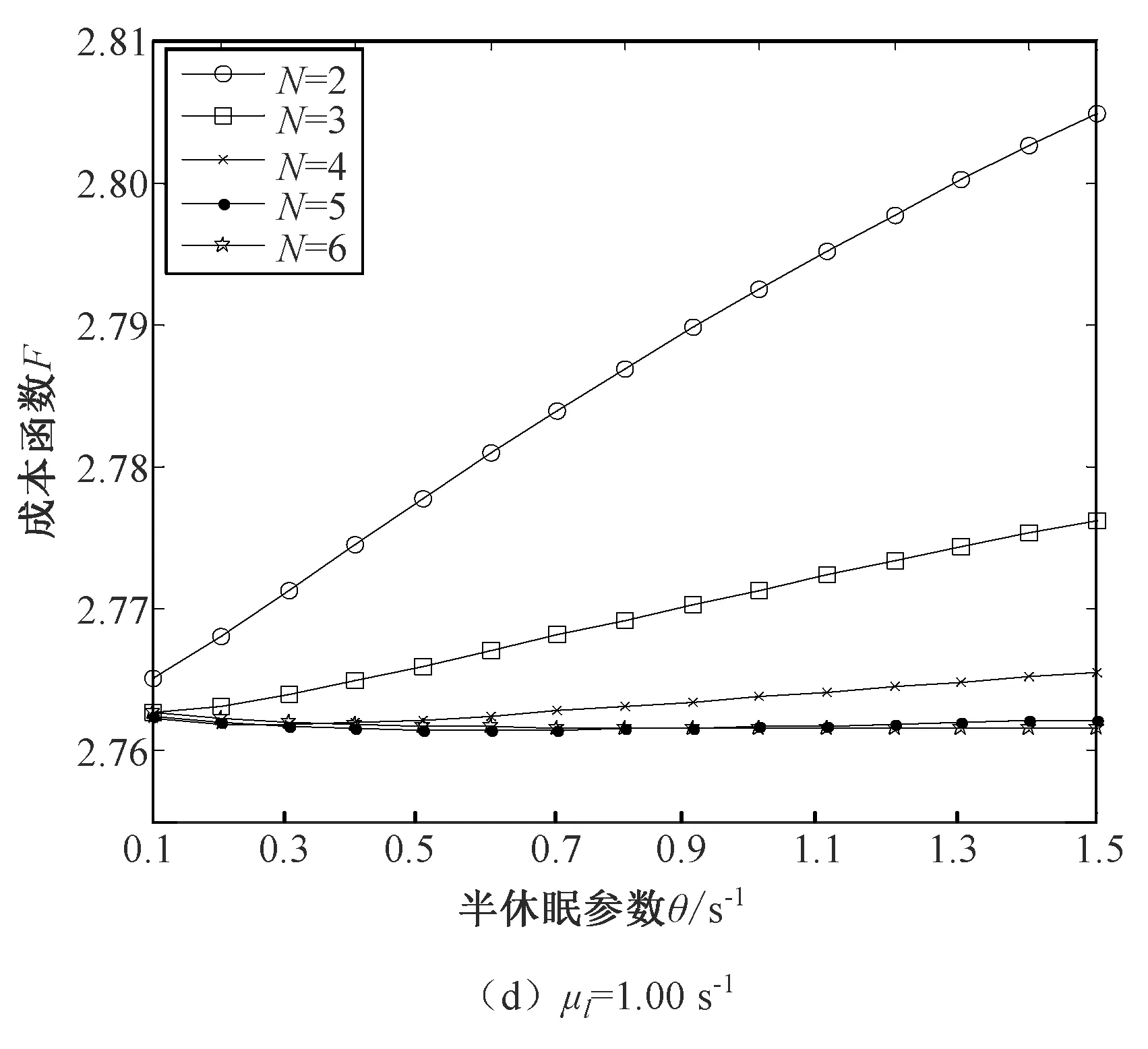
Fig.3 Trend of system cost function
Tab.1 Joint optimization result of wake-up threshold and semi-dormant parameter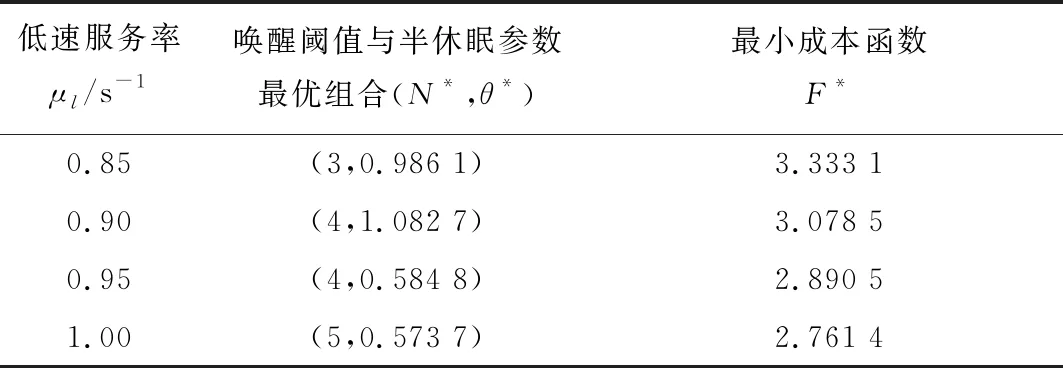
6 结论
