基于信息融合的风电机组老化评估研究

苏连成，邢美玲

(燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

近年来，风电机组的状态监测和维护优化领域的研究取得了很多进展[1-9]。文献[1-4]基于非线性状态估计方法对风电机的状态监测技术进行了研究，文献[5-7]建立了神经网络预测模型，用于判别风电机组异常问题，文献[8]通过支持向量回归的方法对风电机组进行状态评估。传统的风力发电机状态监测技术通常侧重于故障检测和诊断，忽略了老化对风电机组的影响[9]。

风力发电机的使用寿命通常为陆上20～25年，海上25～30年。在使用期间，由于老化效应，其性能和稳定性会随着时间的推移而降低。同时老化效应也会影响能量捕获和风力发电机的可靠性以及运行效率[10]。由于当今运行的大多数现代风力发电机处于使用初期，因此这类问题并未引起太多关注。然而，随着风电机组运行时间的增加，老化现象会逐渐凸显。老化与任何类型的故障不同，它会导致故障的频繁出现，从而增加停机时间和维护成本。因此研究风电机组老化问题对于提高风电机组的寿命管理具有重要意义。为了弥补风电机组在老化问题上研究的不足，本文提出了基于SCADA数据的老化评估准则，用不同评价标准对各个部件进行老化评估。并提出了一种基于神经网络的信息融合方法，对风力发电机整体进行老化评估。最后对所提出的方法进行了验证。

1 SCADA系统

1.1 SCADA系统简介

SCADA系统是数据采集与监视控制(Supervisory Control and Data Acquisition)系统的简称。很多风电场配备了SCADA系统，该系统从风力发电机的关键部件收集数据，以便了解风力发电机的运行状况。SCADA数据具有低采样频率的特点，并不适合进行风力发电机的全状态监测[11-13]。但是低采样率的SCADA数据可以长期描述风力发电机的性能，因此可用于研究风力发电机老化导致的性能退化问题。

1.2 SCADA参数选择

SCADA数据是SCADA系统从风电机关键部件收集的数据，这些数据反映了风电场中风电机的运行状态。但实际风电机组分类众多，从不同类型的风电机组收集到的SCADA参数均不同。例如，本文研究的风电机组是双馈异步风电机组，收集的SCADA数据包括风速，齿轮箱转速，齿轮箱油温，机舱温度，主轴承温度，环境温度等。因此，本研究将首先从这些数据中确定可用于风电机组老化评估的SCADA参数。

为明确地、定量地描述各监测项目之间的相关性，本文引入皮尔逊积矩相关系数，其定义为

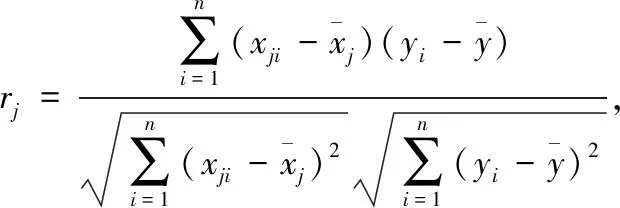
(1)

其中，rj为第j个监测项目与参考对象的相关系数，取值范围[-1,1]，相关系数接近1表明正相关性越强；接近-1表明负相关性越强；而接近0表示相关性越弱[14]。

根据上述理论以7号机组2016年12月份的SCADA数据作为实验样本，分别选取主轴承温度、输出功率、机舱振动、后轴承温度、齿轮箱转速、机舱温度、环境温度、塔筒温度、齿轮箱油泵压力为输出参数，计算各监测项目与输出参数整体发电量的相关系数。根据线性关系系数来研究各组变量间的相关关系，即对整体发电量进行主成分分析。相关系数图如图1所示。

图1 不同SCADA参数的相关系数图
Fig.1 Correlation coefficient diagram of different SCADA parameters

根据图中的系数大小选择出风电机组老化评估的SCADA参数。由图1可知，系数越大两者的相关性越高，与输出参数整体发电量相关性较好的参数分别为主轴承温度、输出功率和机舱振动。所以选取这3个参数作为老化评估参数。

1.2.1输出功率

在一定风速下，输出功率的稳定性是评估风电机组性能的重要标准之一。评估基于以下2个假设，即：在相同的天气条件下(即温度、湿度、风向等)，风电机组在一定风速下产生的功率应大致相同；当风速高于额定风速时，尽管天气条件发生变化，但输出功率应始终接近额定功率[15]。假设风电机组的机舱偏航角始终正确，那么理论上，输出功率的波动基本上取决于空气密度、风速、转子速度和叶片桨距角的变化，计算公式为

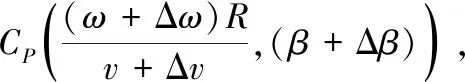
(2)

式中，ΔP表示输出功率的波动，ρ表示空气密度，υ表示风速，R表示转子的直径，CP表示功率系数，ω表示转子的速度，β表示叶片的桨距角。由于风电机组的桨距控制系统仅在风速高于额定风速时才开始工作，所以本文仅选取风速高于额定风速时的数据进行研究。若发电机的转换器正常工作，那么该区域的转子速度应基本保持不变，功率波动ΔP将主要依赖于叶片桨距控制的精度。因此，本文采用输出功率波动ΔP来反映叶片桨距控制系统的老化问题。

1.2.2机舱振动

机舱振动受许多因素的影响，例如外部载荷、塔架及其他支撑结构完整性的影响。一旦这些结构的刚度和阻尼因老化而改变，机舱的振动将随老化程度的增加而增加。若老化发生在服务期间，支撑结构的刚度和阻尼将偏离其原始状态，机舱振动将产生变化。基于这种考虑，本文使用机舱振动来描述塔架和风力发电机的其他支撑结构的性能退化问题。

1.2.3关键部件温度

风电机组的状态监测主要是对其关键设备(如齿轮箱、发电机、主轴承、叶轮、塔架等)进行监测。主轴承的温度是SCADA系统监控风力发电机组的关键数据之一。除了故障情况以外，轴承温度也受外部负载、环境温度和润滑油质量等条件的影响。在使用过程中，润滑油的物理性能和轴承部件的磨损状态都会因老化问题而发生变化，而且外部疲劳载荷和轴电流也会发生变化。当老化严重时，轴承在运转过程中就会发生更多的能量损失，其中一部分以热形式即温度存在。所以当老化程度显著时，主轴承的温度将会增加。因此，本文使用主轴承温度来描述风力发电机主轴承老化问题。

2 评估标准

为了实现风电机组的老化评估，对第1章中确定的3个SCADA参数设计可靠的评估标准至关重要。所以对相应的3个参数进行评估，评估标准δi的表达式为

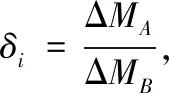
(3)

其中，ΔMB是当风力发电机处于其早期使用寿命时获得的参数(功率波动、机舱振动、主轴承温度等)的基准值，ΔMA是参数的当前值。

为了保证评估的可靠性，借助核密度估计对SCADA获取的数据做进一步处理，从而得到每个参数相应的基准值和当前值。

核密度估计是一种用于估计概率密度函数的非参数检验方法，x1，x2，…，xn为独立同分布F的n个样本点，设其概率密度函数为f，核密度估计可表示为

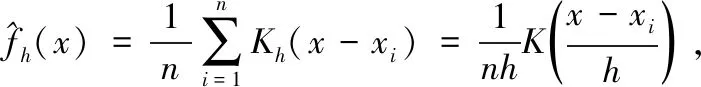
(4)

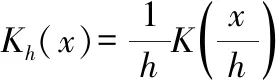
采用某风电场2014年11月份收集到的发电机前轴承温度数据，对此数据进行核函数相同(均为高斯函数)但是窗宽不同的核密度估计。假设e表示窗宽，在不同e值下的核密度估计曲线如图2所示。为确保估计结果的准确，窗宽的选取需要进行多次测试。

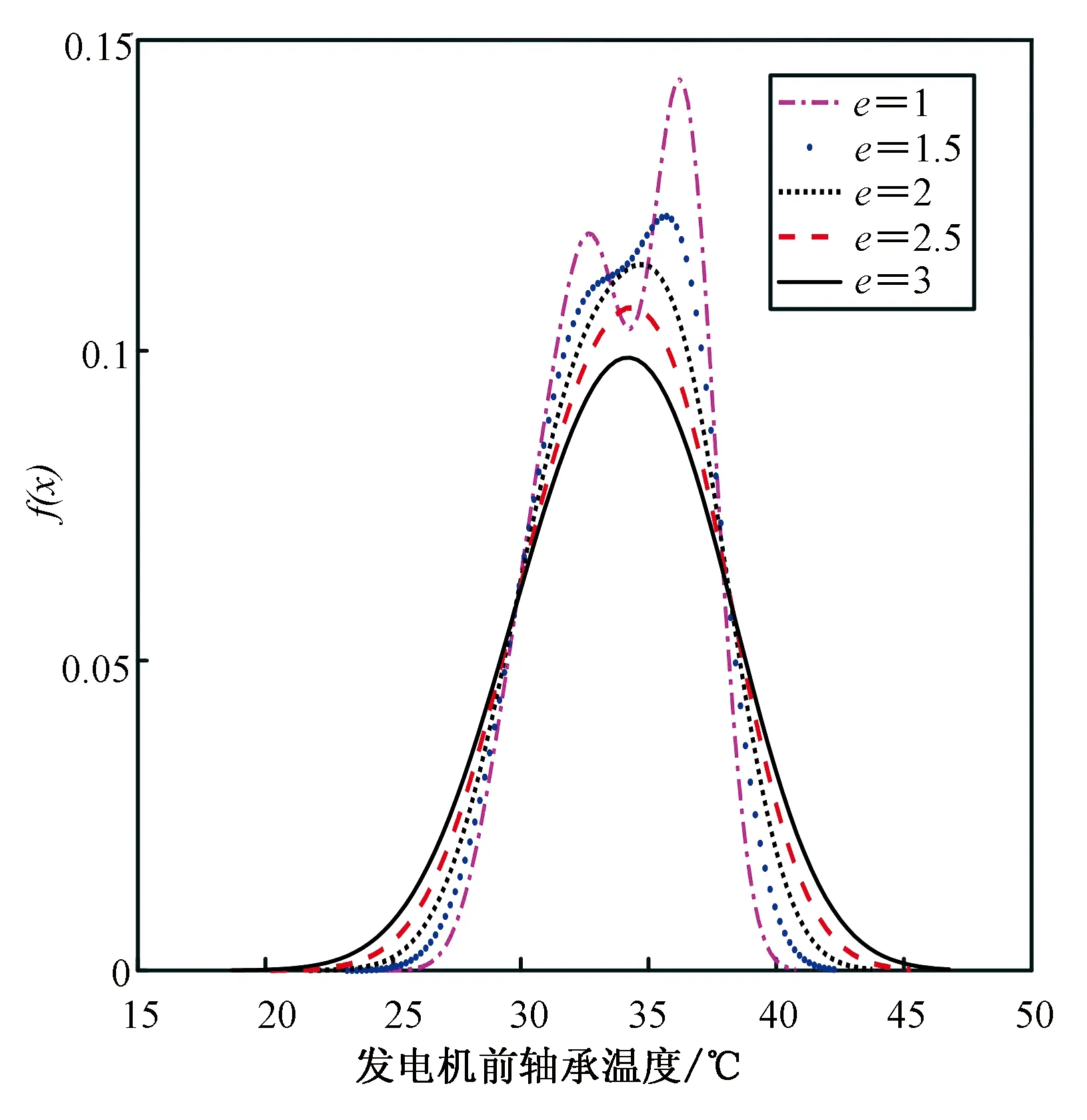
图2 不同窗宽的核密度估计图
Fig.2 Kernel density estimation graphs with different window widths

2.1 输出功率波动评估标准

在计算评估标准之前，应先对SCADA采集到的数据进行处理。由1.2.1节可知用于评估波动的输出功率数据仅是风速高于额定风速时收集的数据。此外，为了确保评估的准确性，无效数据(例如空数据、奇点数据等)以及在风电机组故障和待机时测量的数据应在计算之前去除。经过预处理后用于评估波动的数据可以表示为

Dk=[vki,Pki]，

其中，i=1,2,…,n，Pki为某时刻获得的功率值，并且大于额定功率。k为样本序列号，n为在某段时间内获得的数据总数。那么在此期间输出功率的波动可以通过输出功率的标准偏差来表示：

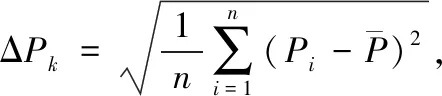
(5)

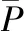
(6)

2.2 机舱振动评估标准

在风力发电机的运行期间，SCADA系统不断地监测机舱的振动。假设在水平和垂直方向上测量的机舱振动分别是vx和vy，则可以从vx和vy推断出风电机支撑结构的性能退化。

用在两个相互垂直的方向上测量的数据vx和vy，可以推导出风电机机舱的合成振动，即

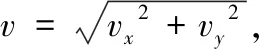
(7)

因此，最终可以获得一系列机舱合成振动数据v={v1,v2,…,vN}。然后，应用由(4)描述的核密度估计方法来识别风电机机舱的可靠合成振动，其对应于核密度曲线上的峰值。可求得机舱振动的评估准则为

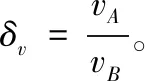
(8)

2.3 主轴承温度评估标准

风力发电机主轴承的温度是通过安装在轴承上的温度传感器进行监控的。考虑到风电机组在不同负载和运行条件下轴承温度可能不同，仅收集在风速达到额定风速时的温度数据。因此，在第k个时间段获得数据集Wk，即

Wk=[vk,Tk]，

其中，vk始终等于额定风速。Tk是在第k个时间段内由传感器收集的温度数据值。重复数据收集，最后获得N组数据进行评估W={W1,W2,…,WN}。同样，应用核密度估计方法获得主轴承温度的可靠估计。可求得主轴承的评估准则为

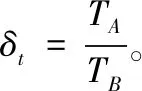
(9)

3 老化评估方法

本文提出了一种基于神经网络的信息融合方法，对风电机组整体的老化情况进行评估。上述3种评估标准在反映风电机组整体性能方面起着不同的作用，因此应该区别对待。为此，需要对每个标准分配适当的加权因子。加权因子能够反映各项标准对于整体评估的关联程度，但是目前公开文献中与此相关的研究甚少。所以为了解决这一问题，本文通过神经网络对加权因子进行合理估算。

假设风速和外界环境变化影响不大，那么风电机组的老化情况将直接影响某段时间内风电机组的整体发电量。所以确定神经网络的输入为输出功率波动、机舱振动和主轴承温度，输出为整体发电量。设置三层神经网络(输入层、隐含层、输出层)，其中输入层神经单元数为3，输出层神经单元数为1，隐含层个数为1，隐含层神经单元数为3。建立神经网络后，需要选择样本对网络进行训练，训练的数据为发电场34号机组2015年11月份的数据，处理后用于训练的数据为3 900个，设置相应的网络参数(最长步数为5 000，目标误差为0.001，学习率为0.3，动量为0.9)，求出第一层(输入层到隐含层)权值输出向量和第二层(隐含层到输出层)权值输出向量，得到权值系数见表1。

表1 权值系数表
Tab.1 Table of weight coefficient

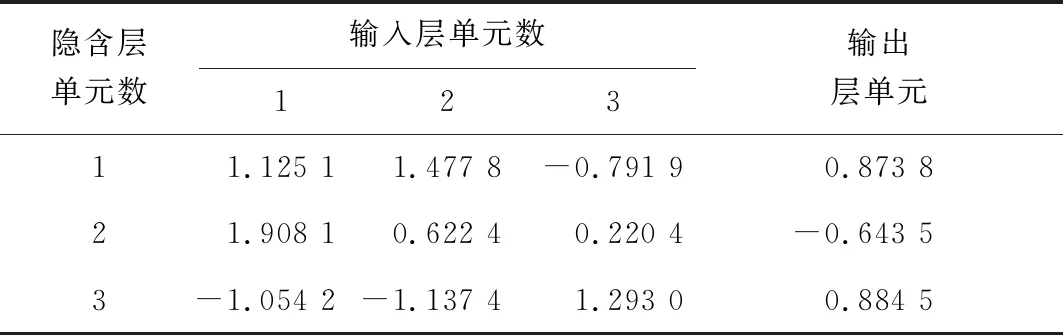
隐含层单元数输入层单元数 123输出层单元11.125 11.477 8-0.791 90.873 821.908 10.622 40.220 4-0.643 53-1.054 2-1.137 41.293 00.884 5

建立神经网络的目的是确定各标准的权重，而神经网络训练得到的结果是各神经元之间的关系，想要得到输入对输出的决策权重，还需要对神经元之间的权重加以分析和处理，所以利用以下公式来描述输入和输出因素之间的关系[16]：

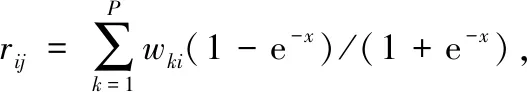
(10)

x=wjk，

(11)

Rij=|(1-e-y)/(1+e-y)|，

(12)

y=rij，

(13)

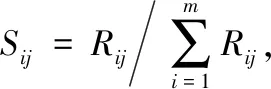
(14)

其中，i为输入单元，i=1,2,…,m；j为输出单元，j=1,2,…,n；k为隐含单元，k=1,2,…,P；wki为输入层神经元i和隐含层神经元k之间的权值系数；wjk为输出层神经元j和隐含层神经元k之间的权值系数，式中Sij就是所求的权重[17]。运用式(10)～(14)可得出输出功率、机舱振动、主轴承温度的权重分别为r1=0.257 6，r2=0.191 2，r3=0.551 2。已求得3个评估准则及其权重，设总体老化评估准则为

δ=r1·δp+r2·δv+r3·δt。

(15)

基于上述讨论，计算和分析老化评估的流程图，如图3所示。

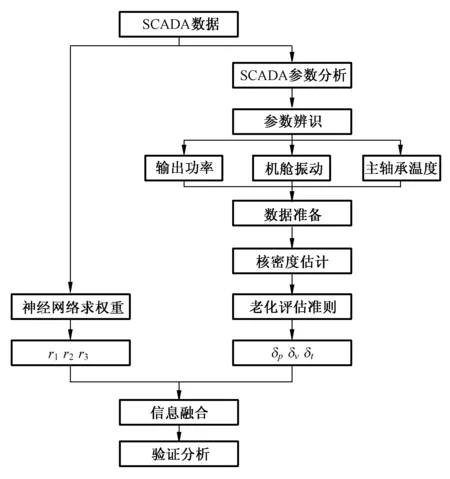
图3 老化评估流程图
Fig.3 Flow chart of aging assessment

首先，通过研究每个标准随时间变化的趋势，对风电机组相应部件的老化情况做具体分析。然后，应用神经网络对每个标准分配适当的加权因子。最后，将这3种信息进行融合求出风电机组整体的老化值。

4 试验验证

4.1 验证过程

为了验证所提出方法的可靠性，选择额定功率为1.5 MW的双馈异步风电机组作为示例，选取7号机组在2015年12月和2016年11月中收集到的5 000组SCADA数据，SCADA系统每间隔30 s采样一次。所选机组安装于2010年。在所研究时间段的区间中，选取了1 000组风速和功率波动数据如图4和图5所示。由图可看出这两年的风速和功率在相同时间的变化形式基本相同，可确保在“基本相同”的控制和操作条件下进行数据估计，从而可以达到更可靠的估计。

在画核密度估计图时，将频率直方图和正态分布密度图放在一起，利于结果的对比。选取收集的5 000组数据，根据式(5)计算功率标准差(参数n取10)，并根据核密度估计获得2015年12月和2016年11月的输出功率波动的核密度曲线，如图6所示。

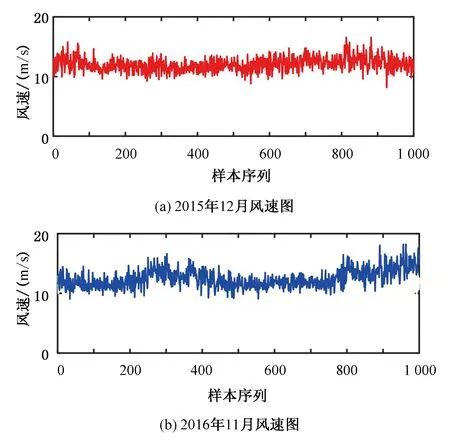
图4 风速对比图
Fig.4 Chart of wind speed comparison

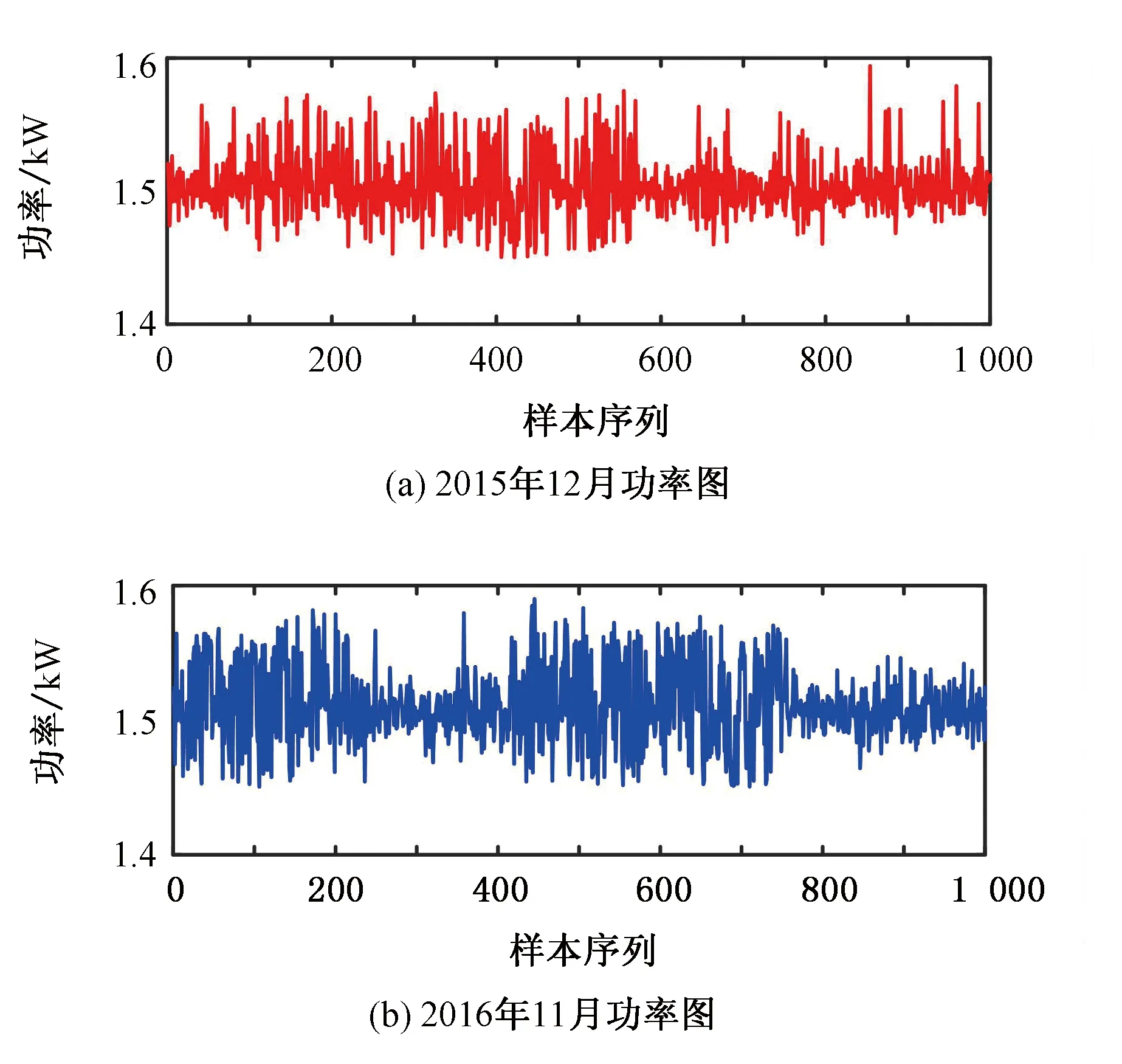
图5 功率对比图
Fig.5 Chart of power comparison

从核密度曲线可知，2015年12月功率波动值为75.186 0，2016年11月为86.429 1。由于核密度估计以最大概率给出了相应的数据值，因此该结果对SCADA数据中存在的不确定性具有鲁棒性。将2015年12月的功率波动的可靠估计值作为基准值，并应用式(6)来计算功率波动准则δp=1.149 5。此数据表明了2016年的功率波动变大，叶片桨距控制系统出现老化现象。然而，常识是风电机组不可能在一年内显示出如此显著的老化程度。因此，单独分析个体老化评估标准不能对风电机组整体老化情况进行可靠评估。

同样，使用这5 000组数据来计算机舱振动和主轴承温度的变化。得到的核密度曲线分别如图7和图8所示。

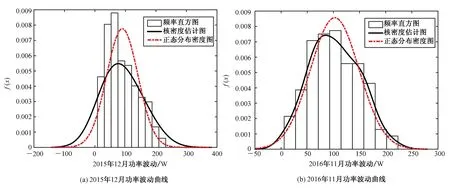
图6 功率波动对比曲线
Fig.6 Comparison curves of power fluctuation

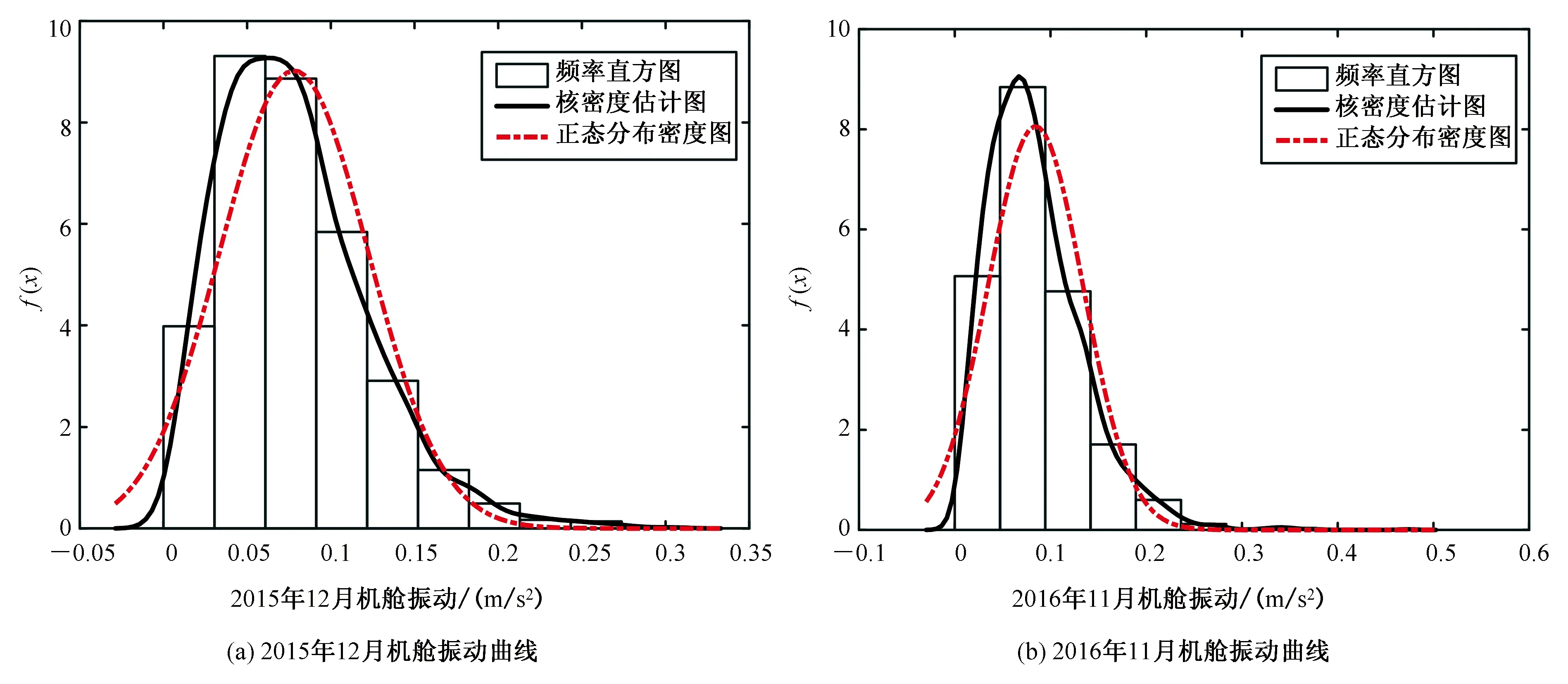
图7 机舱振动对比曲线
Fig.7 Comparison curves of nacelle vibration

由图7可知，2015年12月和2016年11月机舱振动的可靠估计值分别为0.062 5和0.066 9。所以机舱振动准则δv=1.070 4。由数据可知机舱的振动随着时间的变化在增加，可说明在近一年的服务期间，支撑结构的刚度和阻尼偏离了原始状态，塔架和其他支撑结构的性能逐渐降低。

由图8可知，2015年12月和2016年11月主轴承温度的可靠估计值分别为31.918 2和32.510 1。计算出主轴承温度准则δt=1.018 5。数据表明在近一年中主轴承的温度有小幅度的上升，说明主轴承中存在老化现象但是老化程度不高。

由于单独的老化评估标准不能对风电机组整体老化情况进行可靠评估，因此将上述计算结果进行信息融合。将3个老化准则和权重因子r1,r2,r3代入到式(15)中，得到总体老化评估准则δ=1.062 2。显然，这样的结果具有可靠性。所以得出结论，从2015年12月到2016年11月风力发电机存在老化现象。

4.2 改进方法的验证过程

虽然3个评估标准求出的结果真实地反映出了风电机组整体的老化情况，但是由于评估标准较少导致整体老化的综合评价有些误差。因此增加与风电机组老化相关性较好的发电机后轴承温度、齿轮箱转速和机舱温度3个评估标准来提高结果的准确性。

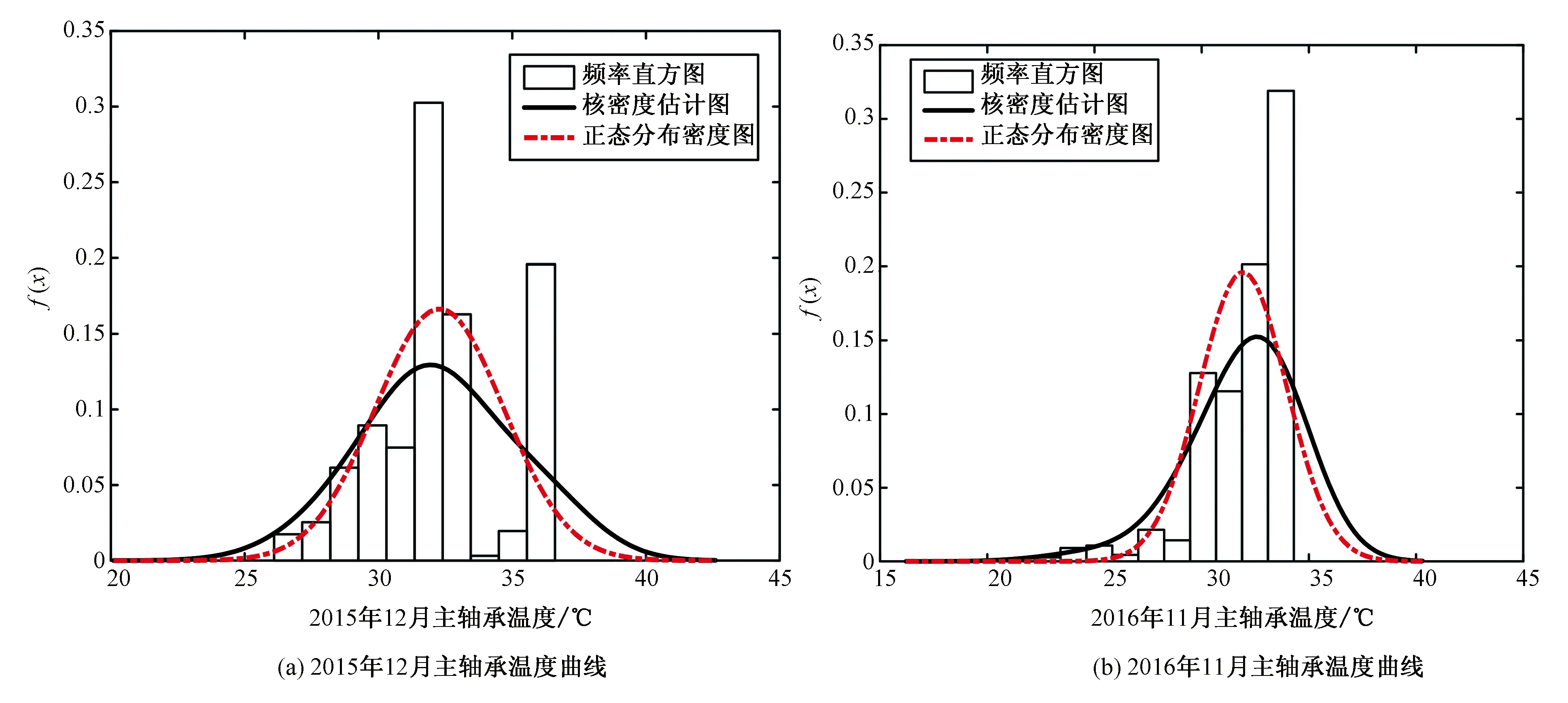
图8 主轴承温度对比曲线
Fig.8 Comparison curves of main bearing temperature

首先根据神经网络算出输入层到隐含层以及隐含层到输出层的权值向量。其中输入层神经单元数为6，输出层单元数为1，隐含层单元数为5。

运用式(10)～(14)可得出功率波动、机舱振动、主轴承温度、发电机后轴承温度、齿轮箱转速和机舱温度的权重分别为r1=0.077 0，r2=0.238 0，r3=0.257 8，r4=0.193 5，r5=0.181 7，r6=0.052 0。使用上述数据重新计算6个评价标准的准则，算出结果分别为δ1=1.149 5，δ2=1.070 4，δ3=1.018 5，δ4=1.028 0，δ5=0.997 0，δ6=1.018 0。进行信息融合可得到整体的老化评估准则δ=1.039 0。显然，这样的结果与3个评价标准的结果相比更加准确可靠。所以讨论风力发电机整体老化性能时，需要考虑更多的与老化相关的评估标准，这样得到的结果更准确。

为了进一步证明所提出的老化评估方法的可靠性，还处理了在同一风电场中另一个风力发电机(15号机组)收集的SCADA数据。15号机组的机型和7号机组完全相同，且安装于2010年。选取15号机组在2015年12月和2016年11月的3 100组数据，统计出两年的评估数据见表2。由此可计算出6个评估准则分别为δ1=1.071 1，δ2=1.154 0，δ3=1.012 0，δ4=1.016 4，δ5=0.997 0，δ6=1.016 0，最终可得到整体老化评估准则δ=1.048 8，数据表明15号机组在所研究的时间段中，存在老化现象，老化程度比7号机组略大。

表2 15号机组评估数据表
Tab.2 Evaluation data table for Unit 15

时间功率波动/W机舱振动/(m/s2)主轴承温度/℃后轴承温度/℃齿轮箱转速/(r/min)机舱温度/℃2015.1276.104 30.051 832.889 955.636 41 605.520.440 92016.1181.516 70.059 833.271 356.551 21 601.220.763 6

选取不同风电场中新装机的34号和36号机组的数据，用来说明提出的老化评估方法也适用于研究未老化的机组。两个机组为双馈异步风电机组，均安装于2013年。选取2014年11月和2015年11月的两个机组各7 000组数据用于研究，运用上述方法根据表3中的数据，可计算得到34号机组的评估准则分别为1.040 0,0.191 2, 0.551 2,0.989 8,1.003 5,0.925 9，36号机组的评估准则分别为1.074 3,0.956 5,0.801 0,0.942 0,1.003 5,0.933 0。由评估准则和相应的权重可计算出34号机组的总体老化评估准则δ=0.948 1，36号机组的总体老化评估准则δ=0.930 1。

结果表明所研究时间段内两个机组还未进入老化阶段。因为两个机组安装于2013年，所以按实际情况来说这两个机组不会出现老化情况，所以实验结果合理且准确。因此，可以得出结论，从2014年11月到2015年11月，34号机组和36号机组尚未老化，并且整体性能有少许提高。

表3 34和36号机组数据统计表
Tab.3 Data statistics table for Unit 34 and 36

机组 时间功率波动/W机舱振动/(m/s2)主轴承温度/℃后轴承温度/℃齿轮箱转速/(r/min)机舱温度/℃342014.1115.533 50.007 029.765 934.619 91 770.622.960 02015.1116.206 50.006 825.134 334.021 21 776.821.257 7362014.1116.494 50.006 929.188 232.277 11 770.025.871 12015.1117.719 50.006 623.030 930.393 61 777.024.138 2

5 结论

本文根据SCADA的监测数据，运用信息融合的方法对风电机组老化问题进行研究。首先，选取功率波动、机舱振动、主轴承温度、发电机后轴承温度、齿轮箱转速以及机舱振动6个SCADA参数作为老化评估标准，以便从不同的角度描述风电机组的老化问题；随后建立神经网络模型求取各个评估标准的权重值；最终，提出一种基于神经网络的信息融合方法对风电机组整体的老化情况进行评估。另外，根据在风电场收集的真实SCADA数据对不同装机时间的机组进行研究，说明了本文提出的基于神经网络的信息融合方法在评估风电机组整体的老化方面确实有效，为机组后期运行和维护提供了参考价值，在延长风电机组的使用寿命方面也具有重要意义。

但此研究仍存在一些问题，由于现有实验数据的局限性，本文提出的研究尚未考虑不同类型的风电机组的老化评估标准。所以在之后的研究中将侧重于区分风力发电机类型，并且还将考虑外部环境因素对风电机组老化的影响。