安达曼海内孤立波的潜标观测分析研究

崔子健,梁楚进,3,蔺飞龙*,金魏芳, 丁 涛, 王 隽

(1.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2.自然资源部 第二海洋研究所， 浙江 杭州 310012；3.南京信息工程大学 海洋科学学院，江苏 南京 210044)

0 引言

内孤立波是在温度、盐度垂向分层的海洋中产生的一种非线性内波[1]，其振幅通常可达几十到数百米，通过影响海水的垂向混合改变海水的热盐结构，在传递大、中尺度动能方面起着重要作用[2-3]。内孤立波通常携带大量能量，在传播过程中可导致部分海面形成强烈辐聚和突发性强流，会对海洋工程、石油钻井平台、海底石油管道和军事潜艇活动等构成严重威胁[4]。因此，海洋中内孤立波的研究一直备受关注。

自内孤立波被首次记录以来[5-6]，关于其生成机制的理论一直在不断发展。已有的研究表明边缘海的内孤立波主要通过潮流和地形的相互作用产生[1,7]，主要包含Lee波[8-9]和内潮裂变[10]两种生成机制。最常见的是Lee波机制[8]：当稳定潮流流经层化海洋时，在海山等凸起的地形后部产生背风波，背风波跨过海山向潮流相反的方向传播，在非线性效应的影响下逐渐发展为内孤立波。内潮裂变机制则是内潮在非线性效应的强化下直接发展为内孤立波[10]。

早期对内孤立波传播的研究大多基于浅水KdV方程或修正的mKdV方程[11-12]。随着研究的深入，科学家发现由于不同的海域水深和层结状态不同，应使用不同的理论进行描述[13]。目前，描述内孤立波传播的方程主要包括浅水KdV方程[14-15]、深水方程[16-17]以及有限深方程[18]，三者根据水深和波长之间的关系，分别适用于浅水、深水和有限深的海洋环境。

安达曼海位于印度洋东北部，安达曼群岛、马来半岛、尼科巴群岛和苏门答腊岛之间[19]，面积约为6×105km2，最大深度达4 419 m[20]，潮汐以半日潮为主导[21]。安达曼海的地形和海水层结状态为内孤立波的产生提供了基础条件[22-23]，是研究内孤立波的天然实验场[24-26]。1965年，PERRY et al[27]首次基于船载观测发现安达曼海南部等温面在短时间内起伏可达40 m，推测其可能由内孤立波引起。安达曼海内孤立波波源的分布是近年来的研究重点之一。OSBORNE et al[1]于1980年通过现场观测结合浅水KdV方程提出安达曼海的内孤立波主要产生于尼科巴群岛和苏门答腊岛北部的浅海区。ALPERS et al[7]利用遥感图像对安达曼海内孤立波进行研究，发现大部分内孤立波产生于安达曼海西部的浅海区域。许明光 等[19]基于数千幅遥感图像绘制了安达曼海的内孤立波分布图，发现了上述地点外另外4个可能的波源位置。近年来数值模拟也被用以研究内孤立波波源位置[28-30]，如BENNEY[12]发现大振幅内孤立波主要是从安达曼海西部岛链的间隙辐射出来的。除现场观测、遥感观测和数值模拟外，BAINES[31]提出的彻体力理论也是研究内孤立波波源位置的重要手段之一。该理论将潮流与地形的相互作用进行量化，可以很好地体现潮流经过复杂地形时激发内孤立波的能力。

目前对安达曼海内孤立波的研究缺乏长时间的连续观测，并且较少涉及其生成机制的探讨。基于此，本文通过潜标实测的温度和流速等数据，对安达曼海中部深水内孤立波的方向、振幅进行分析；应用彻体力理论研究安达曼海的内孤立波波源位置，并与卫星遥感观测结果进行对比；结合内孤立波的传播速度，分析了内孤立波在安达曼海中部海域可能的生成机制。

1 数据和方法

1.1 锚系潜标观测

潜标系统布放在安达曼海中部(位置见图1)，观测时间为2016年6月到2017年7月，观测海域水深约2 670 m，观测区的范围及安达曼海的水深如图1所示。潜标系统由1台声学多普勒海流剖面仪(ADCP，75 kHz，测层厚度16 m)、3台SBE37温盐深传感器、4台SBE39温深传感器、15台SBE56温度传感器、1台安德拉单点海流计和2台声学释放器组成，详细配置见表1，系统总长为2 495 m。

表1 观测站位锚系潜标配置Tab.1 Design of the mooring system

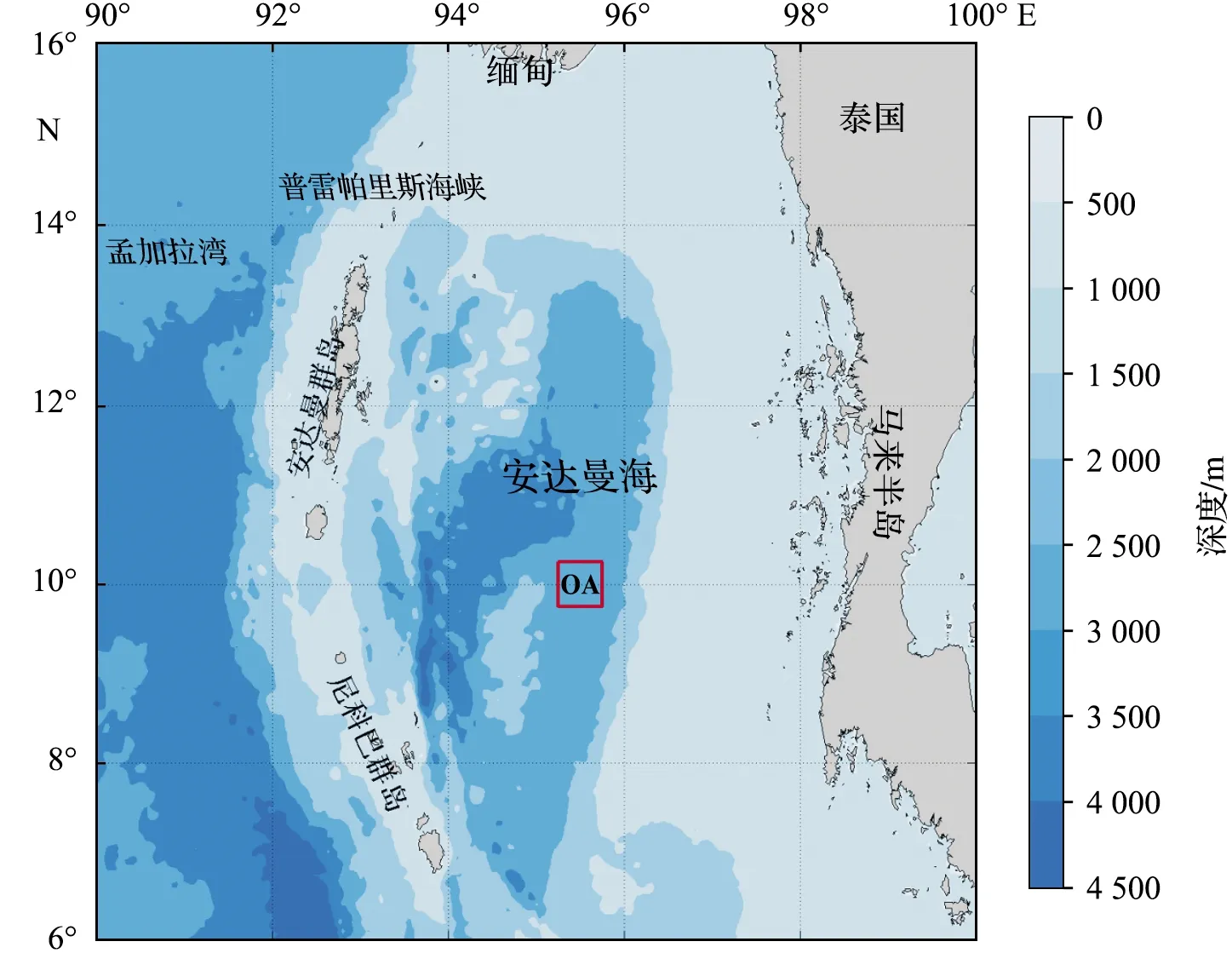
图1 观测范围及安达曼海水深图Fig.1 Observation area and the depth of the Andaman Sea (红色方框为潜标观测位置以及附近海域。) (The red box indicates the observation area by mooring system.)

对温度数据进行月平均处理，插值得到各温度剖面时间序列，其中17 ℃等温线的起伏最为明显，将其变化作为内孤立波的判定依据。如30 min内该等温线的深度变化幅度超过20 m，判定为有内孤立波发生，深度变化幅度定义为其振幅。在内孤立波数量统计时，剔除不同振幅的重复记录。对ADCP流速数据进行3阶高通滤波处理，使波致流不受半日潮和全日潮的影响。半日潮频率选取区间为1/(1.2×12×60×60) s-1～1/(0.8×12×60×60) s-1。

1.2 SAR卫星遥感图像

本文所使用的卫星遥感图像是基于ScanSAR模式的HH极化图像，来自日本先进陆地观测卫星2号(ALOS-2)，分辨率为25 m，图像时间为2016年12月4日5时29分。

1.3 Argo再分析数据集

安达曼海的温度、盐度背景场数据来自中国Argo实时资料中心(http://www.argo.org.cn/)的全球海洋(79.5°S—79.5°N，180°W—180°E)Argo温度、盐度月平均剖面资料，数据时间为2004年1月—2017年12月。该资料集通过线性插值法将温度、盐度进行垂向插值到标准层(56层)，水平分辨率为 1°×1°。

1.4 内孤立波波源计算

BAINES[32]认为海底地形的高度、形状和宽度均会影响特定水体激发内波的能力，在此基础上提出了彻体力理论，计算潮流和海底地形相互作用产生内波的能力，公式如下

(1)

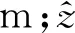
将公式(1)中的F值从海表到海底垂向积分，得到新的F值表达式：

(2)

全剖面的浮力频率N通过Argo再分析数据计算获得，公式如下

(3)

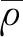
将研究海域(6°N—16°N，90°E—100°E)以0.2°×0.2°的网格进行划分，通过全球海洋潮汐模型TPXO9[33]获取4个半日潮(M2、S2、N2、K2)和4个全日潮(K1、O1、P1、Q1)在每个网格点上的潮流水平流速u(向东为正)、v(向北为正)分量，时间为2017年3月。海底地形坡度数据来自美国地球物理中心(National Geophysical Data Center，NGDC)的ETOPO2地形高程数据(https://www.ngdc.noaa.gov/mgg/global/etopo2.html)。根据公式(1)计算F值，按公式(2)再对F值进行从海表到海底的垂向积分。

根据潜标观测的内孤立波的传播方向，选择3个可能的波源位置并计算各分潮的F值，位置分别为L1(10°N，93°E)、L2(9.2°N，93°E)和L3(7°N，94°E)。

1.5 内孤立波波形的模拟和一阶非线性相速度的计算

用浅水KdV方程、深水方程和有限深方程分别对内孤立波的波形进行模拟。浅水方程和深水方程的垂直分层为2层，有限深方程为58层(深度200 m以浅，层厚为10 m；200～500 m之间，层厚为20 m；500～1 300 m，层厚为50 m；大于1 300 m，层厚为100 m)。三种方程中内孤立波的最大振幅η0均取38 m，即2016年12月4日实测的17 ℃等温线的最大起伏。各方程的解析解如下

(1)浅水KdV方程的解析解为[11]

η=-η0sech2(φ)

(4)

其中：η为波振幅，η0为最大振幅，单位：m。φ为相位角，φ=(x-Vt)/L，其中V为非线性速度，单位：m/s；L为特征半波宽，单位：m。V和L的计算方法分别为

V=c1+α1η0/3

(5)

L=(12β1/α1η0)1/2

(6)

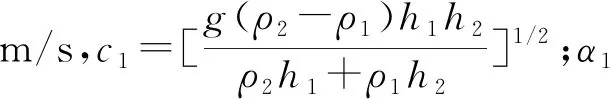
(2)深水方程中内孤立波的解析解为[11]

(7)

上、下层水体厚度、密度、时间步长取值均与浅水方程相同。

(3)有限深方程中内孤立波的解析解为[7]

(8)

其中：a和b是类似波数的参数，通过下式计算得出：

abtan(aH0)=1

(9)

(10)

其中：H0为最大深度，单位：m；βF为斜压频散参数，计算公式如下

(11)

其中：z表示深度，单位：m，Z0是波函数W最大值所在的深度。波函数W通过下式计算：

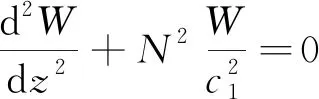
(12)

2 结果

2.1 安达曼海中部内孤立波的观测与分析

潜标系统在2017年3月4日8时40分左右捕捉到观测期间的最大振幅内孤立波。根据17 ℃等温线的起伏推测其振幅达100 m，此时最大流速达到了0.81 m/s，方向为北偏东68.43°。图2显示了该内孤立波发生前后1.5 h的温度剖面，流速u、v分量的变化。17 ℃等温线深度在10 min内急剧下降100 m左右，并在15 min内再次回到其初始位置；流速的东分量(u)和北分量(v)在25 min内迅速超过了0.4 m/s，其中u分量最大，可达0.6 m/s。

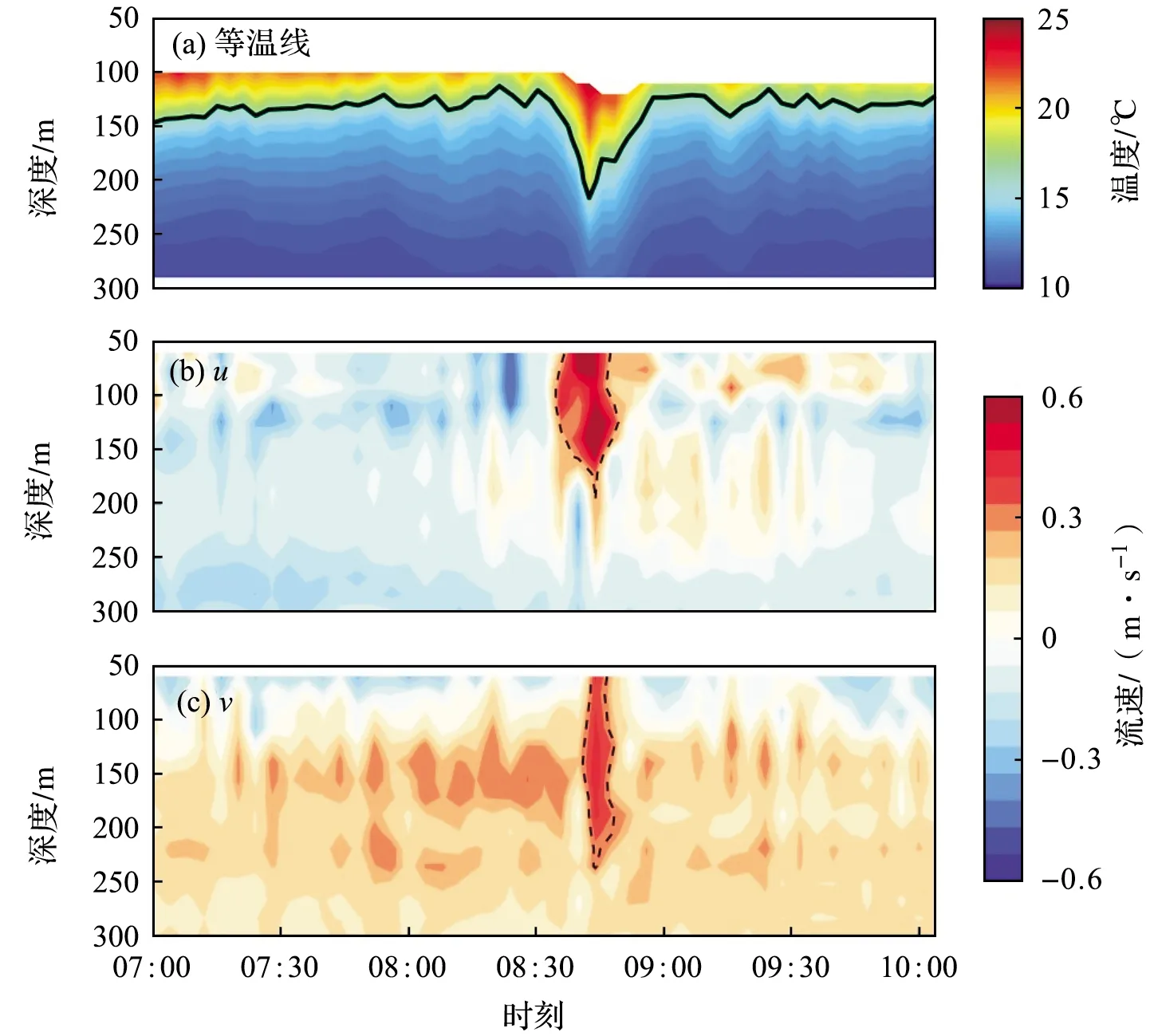
图2 潜标系统在2017年3月4日观测到的最大振幅内孤立波的等温线(a)、流速u分量(b)以及流速v分量(c)等值线图Fig.2 The isotherm(a), u component of current velocity(b) and v component of current velocity(c) of the internal solitary wave with maximum amplitude observed by mooring system on March 4, 2017 (图a中黑线为17 ℃等温线。图b和c中黑色虚线为0.4 m/s等值线。) (The black line indicates the 17 ℃ isotherm inFig.a. The dotted lines indicate the contour line of 0.4 m/s inFig.b and c.)

潜标观测期间，振幅>20 m的内孤立波发生1 900次，振幅>30 m的发生426次，振幅>40 m的发生105次，振幅>50 m的发生26次，振幅>60 m的发生7次。其中振幅>60 m的大振幅均向东北传播，方向介于北偏东16.92°～68.43°之间(图3)，最大流速介于0.61～0.84 m/s之间。振幅>20 m的同样以东北向传播为主，方向为北偏东55.92°。

2.2 内孤立波波源的分布

研究海域半日潮引起的F值分布如图3所示，其中大尼科巴岛东南、卡尔尼科巴岛附近以及普雷帕里斯海峡南部等地F值较大(F>6)。F的最大值为 9.901 5，位于普雷帕里斯海峡南部附近海域。在普雷帕里斯海峡南部有两处F值>6，彼此间不关联，表明该处可能存在2个内孤立波波源。与半日潮相比，全日潮引起的F值较弱(图略)。

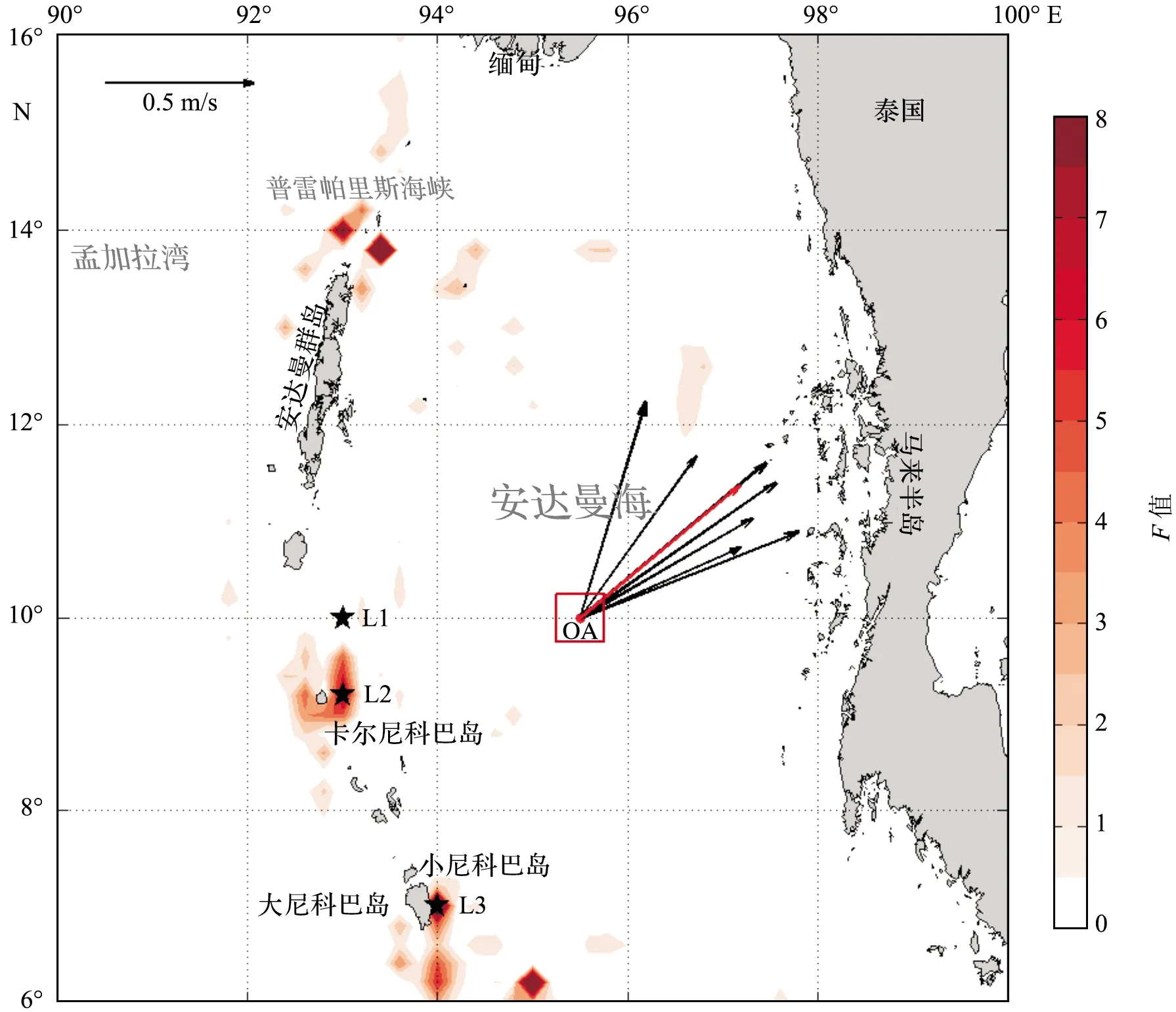
图3 半日潮引起的F值在安达曼海的分布以及研究区内振幅大于60 m的内孤立波Fig.3 The distribution of F caused by semidiurnal tides in the Andaman Sea and the internal solitary waves with amplitude greater than 60 m (红色斑块表示F值。红色方框为潜标观测及附近海域。箭头表示内孤立波，箭头长度表示流速大小，箭头方向表示波 的传播方向。黑色箭头表示潜标观测到的振幅大于60 m的内孤立波，红色箭头表示这些波的平均流速和传播方向。 L1、L2和L3为假定的潜标观测到内孤立波的波源位置。) (The red patchs indicate F value. The red box indicates the observation area of mooring system. The length and direction of the arrow indicates the current velocity and the propation direction of internal solitary waves. The black arrows indicate the internal solitary waves with amplitude of >60 m, the red arrow indicates the average propagation direction and the current velocity. L1, L2, and L3 are the assumed source positions of the internal solitary waves observed by the mooring system.)

8个主要分潮在3个可能的波源位置(L1，L2，L3)引起的F值见表2。L2和L3处的F值较大，L1处的F值较小；全日潮各分潮(K1，O1，P1，Q1)引起的F值较弱，约为半日潮(M2，S2，N2，K2)引起的F值的1/5。在4个半日潮分潮中，M2分潮引起的F值最大，是影响该海域F值的主导分潮。各分潮在不同位置引起的F值存在差异，大部分分潮在L3位置处的F值大于L2，但O1和Q1分潮的结果相反。

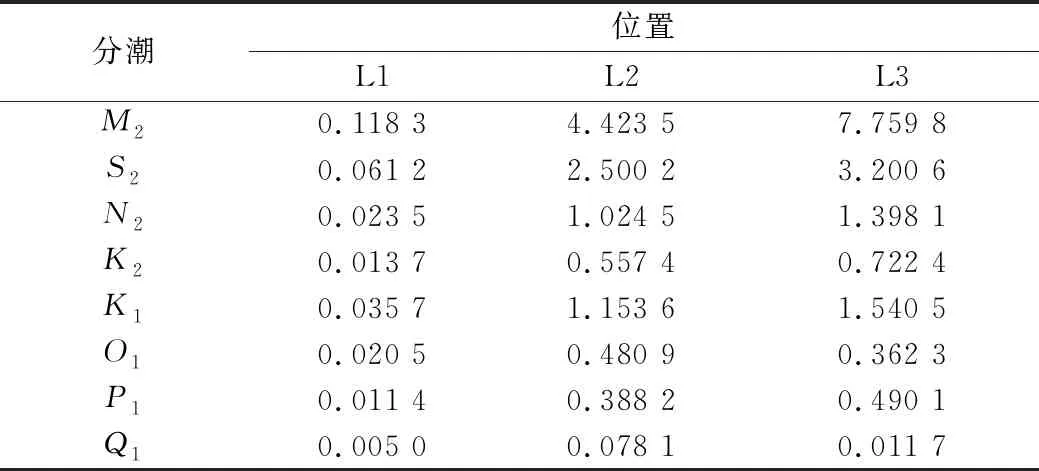
表2 主要半日潮和全日潮分潮在L1、L2和L3 位置引起的F值Tab.2 F values caused by main semidiurnal tides and diurnal tides at the locations L1, L2 and L3

2.3 潜标观测结合遥感图像计算内孤立波相速度

图4为2016年12月4日安达曼海的卫星观测图像，存在3处明显的内孤立波波峰。第一个和第二个波峰(自右向左)相距约37.2 km，两者在潜标中出现的时间相差约10 h，由此推算出第二个内孤立波传播的相速度约为1.03 m/s。同理，第二个和第三个内孤立波波峰相距约46.2 km，经过潜标位置的时间差约为10 h，则第三个内孤立波的传播相速度约为1.28 m/s。

图4 2016年12月4日观测海域附近的卫星遥感图像Fig.4 The remote sensing image near the observation area on December 4, 2016 (图中红色方框为潜标观测及附近海域。) (The red box indicates the observation area.)

2016年12月4日—5日，潜标的温度、流速如图5所示。图中3个内孤立波的振幅均在40 m左右，出现的间隔约为10 h。第一个内孤立波经过时，最大流速为0.48 m/s，方向为北偏东69.15°。

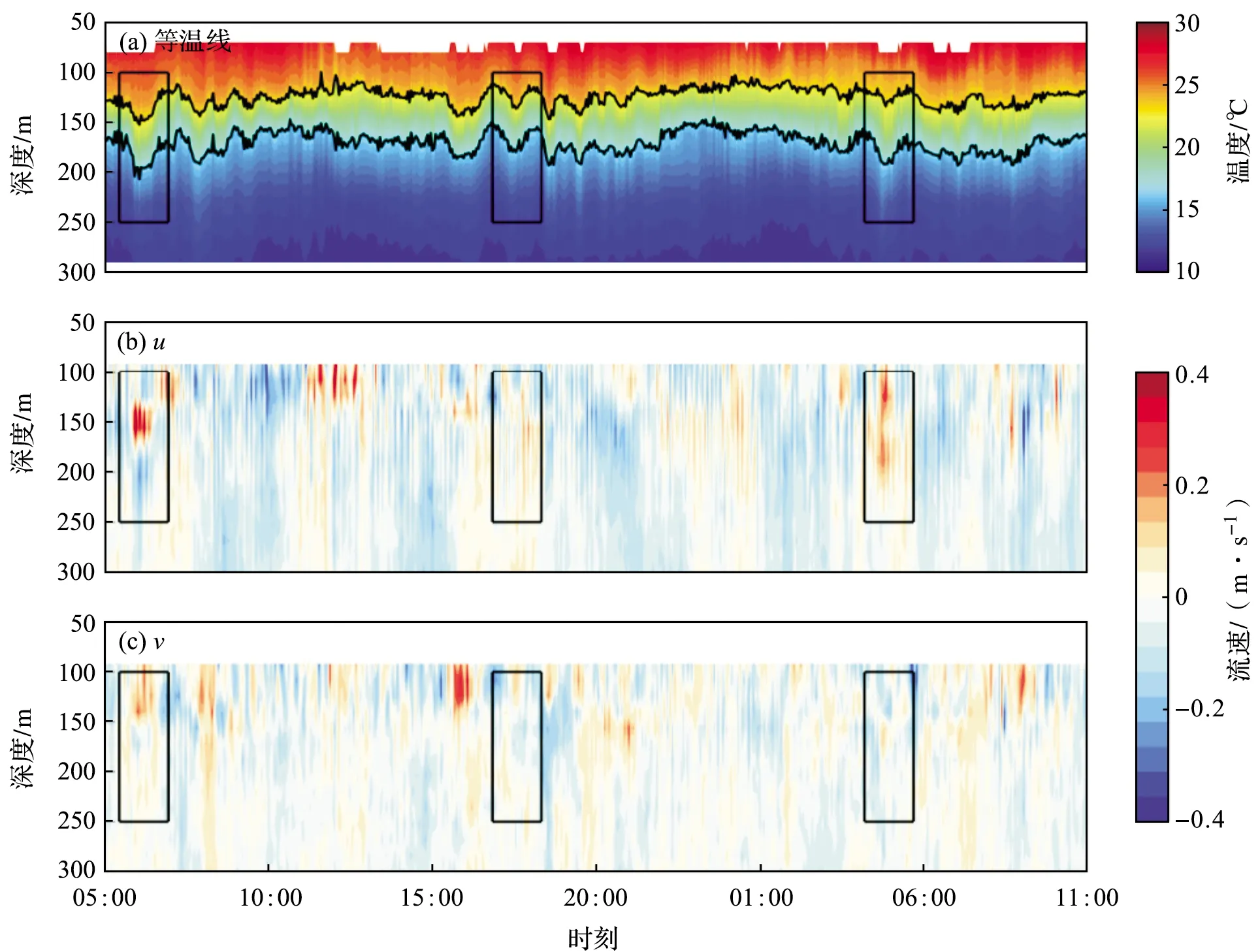
图5 潜标系统在2016年12月4—5日观测到的等温线(a)、流速u分量(b)以及流速v分量(c)等值线图Fig.5 The isotherm(a), u component of current velocity(b) and v component of current velocity(c) of the internal solitary wave observed by mooring system on December 4-5, 2016 (图a中上下两条黑线分别为23 ℃和17 ℃等温线。黑框为内孤立波经过时温度和流速的变化。) (The black lines from top to bottom indicate the 23 ℃ and 17 ℃ isotherm, respectively inFig.a. The black boxes are the change of temperature and current velocity when the internal solitary waves passed by.)

2.4 三种方程对安达曼海内孤立波振幅和相速度的 模拟

应用浅水KdV方程对安达曼海内孤立波的振幅进行模拟，计算显示该内孤立波的振幅远远超过潜标所在海域的最大水深，与事实明显不符，表明该方程不适用于描述该海域的大振幅内孤立波现象。

应用深水方程和有限深方程对2016年12月4日内孤立波的模拟结果如图6所示。有限深方程模拟的波形与潜标观测结果最一致，表明其计算的相速度最接近潜标观测结果。深水方程的模拟结果与有限深方程类似，但波形更加陡峭，表明其计算的相速度明显大于潜标实测数据。

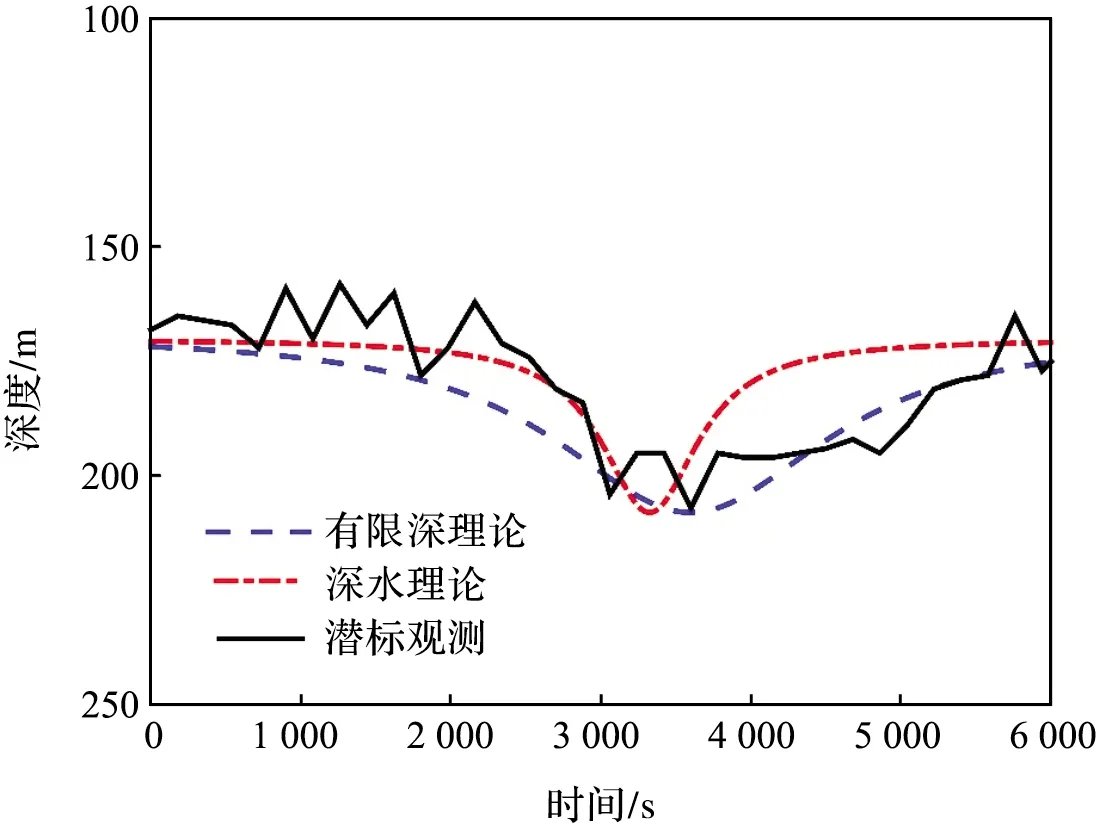
图6 2016年12月4日5时—7时的内孤立波振幅 观测及模拟结果Fig.6 The observation and simulation of the internal solitary wave during 5-7 am, December 4, 2016

分别用深水方程和有限深方程对2016年12月4日出现的第一个内孤立波的一阶斜压非线性相速度c1进行计算，结果分别为c1=3.16 m/s和c1=0.97 m/s。与潜标实测的相速度c1=1.03 m/s相比，显然有限深方程计算的结果c1=0.97 m/s更接近实测。如果某一内孤立波从L2位置(距潜标约300.78 km)发出，根据相速度c1=0.97 m/s计算，该内孤立波从波源传播到达潜标位置所需的时间大致为68.74 h(约3 d)。

假设L2位置(卡尔尼科巴岛以东，9.2°N，93°E)为2016年12月4日出现的内孤立波的产生源地，根据流速u分量和内孤立波到达潜标位置的时间，推算其在源地L2的生成时间，如图7所示。图7a为TPXO9模型预报的潮流时间序列，图7b为潜标观测到内孤立波的时间，斜线表示潜标观测到内孤立波的传播时间(68.74 h)。内孤立波的出现周期与半日潮周期基本一致，其在L2的生成时间与潮流u分量向西极大值的出现时间基本吻合。该结果表明，当潮流向西传播流经安达曼海西侧岛链时，在岛链的另一侧产生内孤立波，向东传播至观测海域。这种内孤立波的生成机制属于典型的Lee波机制。

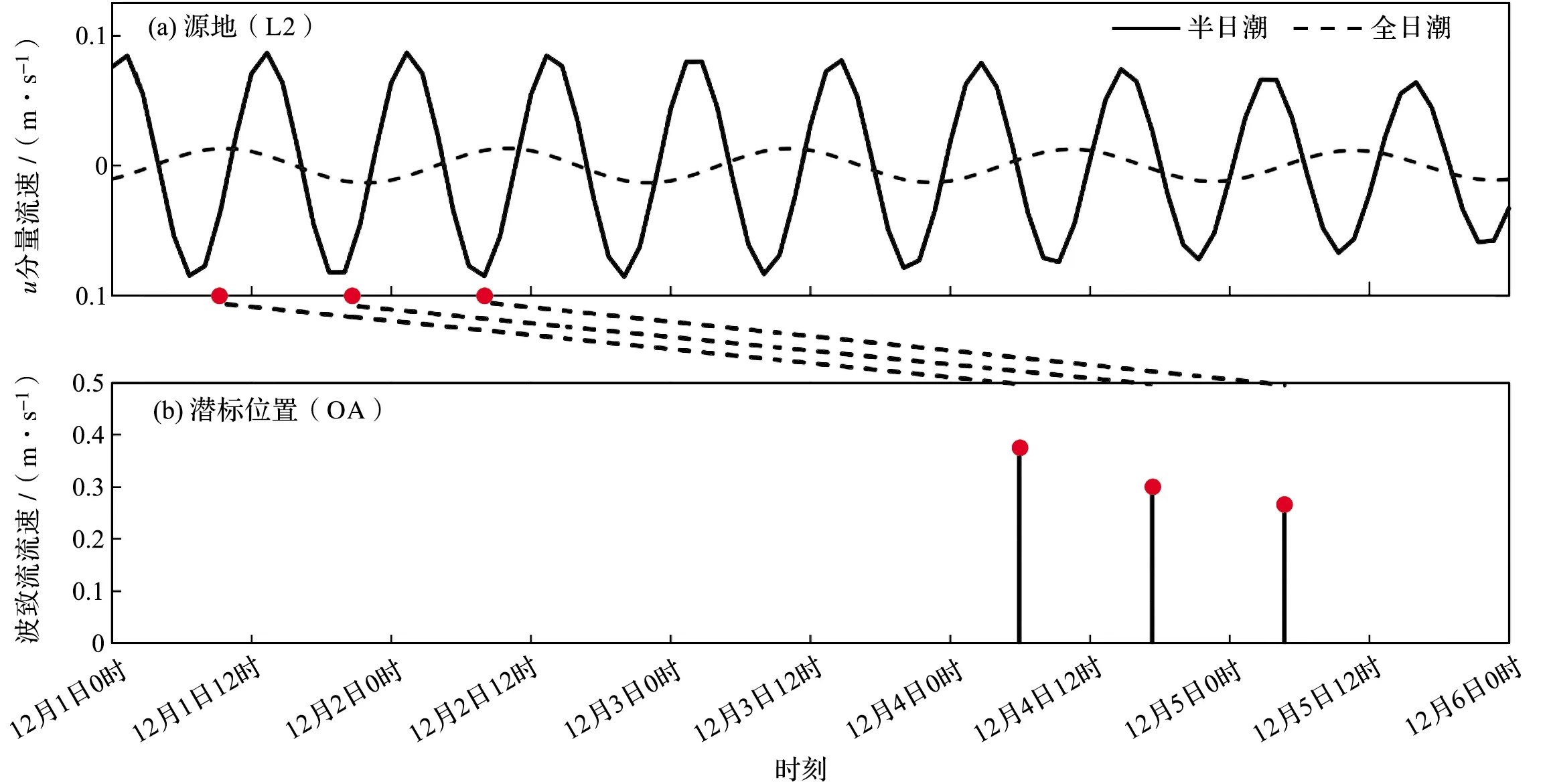
图7 2016年12月1日—6日L2位置的半日潮、全日潮的潮流u分量预报值(a)以及潜标位置捕捉到 内孤立波的时间及最大流速大小(b)Fig.7 The prediction of u component of tidal current at the location of L2 for semidiurnal and diurnal tides on December 1-6, 2016(a) and the time of internal solitary waves and the largest current velocity observed at the position of the mooring system(b) (斜线表示内孤立波传播时间。) (The oblique line represents the propagation time of the internal solitary wave.)

3 讨论

F值计算结果表明，在安达曼海普雷帕里斯海峡南部、卡尔尼科巴岛、大尼科巴岛附近是主要的内孤立波波源，与已有的卫星遥感统计分析[26,31]一致。本文研究显示普雷帕里斯海峡南部是2个内孤立波波源的叠加，这与前人基于卫星遥感图像的1个波源的结论相比可能更为精确[26,31]。该理论方法相比遥感统计更加简单，可经卫星遥感验证后广泛应用于内孤立波多发的各个海域。小尼科巴岛北部海域无明显的波源，这或许与全球海洋Argo温度、盐度剖面资料的空间网格精度较低有关，尤其在岛屿密集的海域往往存在温、盐数据的缺失，导致无法计算F值。

安达曼海观测海域内孤立波的传播用有限深方程模拟效果最佳，而浅水KdV方程的计算结果与实测相差较大。之前的研究也表明KdV方程更适用于模拟浅水海域的小振幅内孤立波，而对深水大振幅内孤立波的模拟则准确性较低[34]。对于有限深方程和深水方程，有学者研究认为在深海分层流体中，两个来源内孤立波的弱相互作用是可以受两种理论独立支配的[35]。

本文在深水方程和有限深方程的计算中对海水层结状态进行了简化，因此两个方程的模拟结果并不能完全反映海洋的真实状态。前人研究发现内孤立波在经过安达曼海中部的海脊时振幅有可能变大[36-37]，使相速度c1出现一定偏差，传播时间也与实际不同。如CAI et al[38]在对南海内孤立波的研究发现，由于不同区域海水分层状态差异较大，相速度和波长的近似计算可能存在较大误差。潜标等实测数据和数值模拟的结合有助于更加清晰地认识安达曼海内孤立波的生成、传播与演化。与卫星遥感观测相比，潜标观测具有高时间分辨率的优势，可以不间断地记录观测区域的内孤立波信息，极大地弥补了遥感研究的不足。

4 结论

本文通过2016年至2017年在安达曼海中部布放的锚系潜标的数据对目标海域内孤立波的方向和强度进行了研究，得到以下主要结论：(1)观测海域有大量向东和东北方向传播的内孤立波，最大振幅可达100 m。(2)使用浅水KdV方程、有限深方程和深水方程模拟内孤立波波形，结果显示三种方程中浅水KdV方程的模拟结果与实测差距较大，深水方程和有限深方程的模拟与实测较符合，其中有限深方程模拟的波形、流速以及一阶斜压非线性相速度均与潜标或遥感观测结果相符。(3)通过内孤立波波源位置、强度以及速度等研究，认为安达曼海内孤立波的生成机制可能为Lee波机制。