区域多机场系统辐射域竞争均衡模型研究

胡夏婷，曾小舟，潘怡凡

（南京航空航天大学民航学院，江苏 南京211106）

随着经济及社会的发展，我国民航运输体系已初具规模，民用运输机场数量也随之增加。 截止2018 年底，我国共有民航运输机场235 个[1]。 经济发达的长三角、珠三角地区，其机场密度已达到每万平方公里1.09，2.37 个。而世界典型机场群的机场密度，如纽约机场群、伦敦机场群，仅为0.43 及1.11 个。因此，机场群协同运行已成为我国区域机场运行面临的新问题， 对我国机场群进行辐射域竞争均衡研究具有重要意义。

随着机场密度的持续增加，区域多机场系统也随之出现。 区域多机场系统指区域内地理位置相邻的机场之间，为实现区域资源的有效分配及协调管理，形成具有一定竞争和协同关系的机场群。

机场腹地（hinterland）是为机场提供客流和货流的内陆地区，又称为机场的吸引范围、吸引地，其内涵是机场吸收和辐射能力能够达到并能促进其经济发展的地域范围[2]。本文所指的机场腹地是从空间角度出发，基于机场综合实力的地理辐射和经济辐射范围。

目前，对区域多机场系统的研究主要以机场间的竞争与协作为背景，以提升系统运作效率为目标，分析机场的功能划分及发展现状等[3-6]。 机场腹地的研究则以测算辐射范围为主：一类从城市空间相互作用角度出发，使用传统理论模型[7]、引力模型及其衍生模型[8]进行测算，也有学者基于空间分割原理，使用城市断裂点模型[9]或加权Voronoi 图[10]，对机场辐射范围进行研究；另一类则从旅客选择角度出发，使用非集计模型[11]等确定机场市场份额，得到辐射范围。

上述研究均取得了一定成果。但目前，针对机场辐射域交叉部分的竞争均衡研究还较少，而机场间腹地交叉区域的竞争和协同才是机场竞争的重点。 因此，本文以Lotka-Volterra 模型为基础，对区域多机场系统内的交叉腹地进行竞争均衡研究。引入机场综合实力为影响因子，从空间角度出发确定各机场的腹地范围；以腹地交叉区域的市场份额变化趋于稳定为均衡，构建竞争均衡模型，进而求解两机场间的竞争稳定状态及满足条件。 最后，以长三角机场群为例，对南京禄口机场、杭州萧山机场的辐射域交叉部分进行仿真，分析其竞争情况和可能的均衡结果，为机场提升在区域多机场系统内的竞争力明确方向。

1 竞争均衡模型构建

1.1 模型建立

20 世纪40 年代，美国生态学家Lotka 和意大利数学家Volterra 分别提出了生物数学经典模型，即Lotka-Volterra 模型。 该模型通常被用于描述生态系统中两种群间的种群规模演变过程，涉及的种群关系包括种间竞争、捕食与被捕食、寄生与共存。 Lotka-Volterra 模型的一般形式为

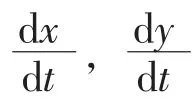
该模型由于其一般性被广泛运用，但同时，由于种群间的关系较多，包括种间竞争、捕食与被捕食、寄生与共存等，许多学者也随之对Lotka-Volterra 模型进行了改进。

对于区域多机场系统而言，机场之间普遍存在腹地交叉区域，该区域内的旅客拥有机场的自主选择权。对旅客来说，可选择的机场之间是存在竞争关系的。 同时，旅客是否选择某一机场与该机场的陆侧交通、航班数量、票价等密切相关，有学者将这一系列影响因素整合为机场综合实力[8]。 因此，为了定量描述机场的竞争情况和可能的均衡结果，本文基于机场综合实力这一影响因子，运用Lotka-Volterra 竞争模型进行分析。具体模型如下：

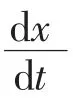
1.2 竞争均衡模型求解

根据式（2），本文对该模型求解其平衡点，使用雅可比矩阵对平衡点进行稳定性分析，最终得到具有稳定性的平衡点及其所需条件，并对竞争情况和可能的均衡结果进行分析。 在求得的具有稳定性的平衡点时，两机场市场份额的变化率趋于稳定，同时市场份额达到均衡，该种状态即为两机场间的竞争稳定状态，也是本文所需的最终结果。

令系统时间t→+∞，通过微分方程组（2）得到代数方程组（3）：

1.3 平衡点分析

对求得的具有稳定性的平衡点做进一步分析：

1） 当腹地交叉区域内的旅客对机场1 的需求量d1大于机场1 对机场2 的竞争系数γ12， 即1-γ21d1＜0时，点K2（d1，0）具有稳定性。 考虑旅客对机场2 的需求量d2及机场2 对机场1 的竞争系数γ21的大小关系，即考虑1-γ12d2＜0 或1-γ12d2＞0 的情况。

从坐标轴原点o 出发，机场1 及机场2 市场份额的变化率均大于0，故两机场的市场份额持续增加。 增加到两线交点时，两机场的市场份额达到均衡状态，虽然该交点处为两机场的平衡点，但这种状态很不稳定。 在交点两侧由实线、虚线和坐标轴构成的三角形区域内，机场2 市场份额的变化率仍大于0，因此该机场的市场份额会持续增长，而机场1 市场份额的变化率小于0，因此其市场份额会逐渐减少。经过时间t 后，两机场的市场份额均停止增长，机场2 在竞争中获得最大市场份额，机场1 被淘汰。

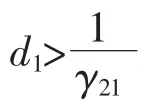
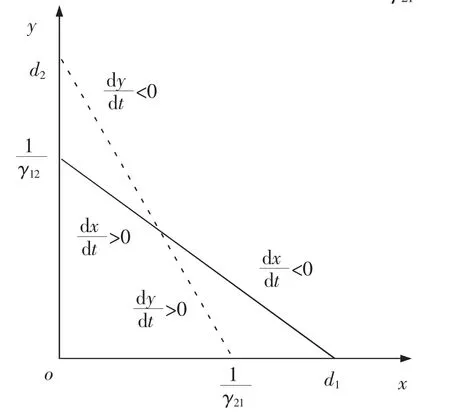
图1 条件1）a 时两机场竞争状态图Fig.1 The competition state diagram of two airports at Condition 1）a

图2 条件1）b 时两机场竞争状态图Fig.2 The competition state diagram of two airports at Condition 1）b

从坐标轴原点o 出发，机场1 及机场2 市场份额的变化率均大于0，故两机场的市场份额持续增加。 在实线、虚线和坐标轴构成的梯形区域内，机场2 市场份额的变化率开始小于0，因此其市场份额会逐渐降低，而机场1 市场份额的变化率仍大于0，故市场份额会持续增长。 经过时间t 后，两机场的市场份额均停止增长，机场1 在竞争中获得最大市场份额，机场2 被淘汰。

2） 当腹地交叉区域内的旅客对机场2 的需求量d2大于机场2 对机场1 的竞争系数γ21时， 即1-γ12d2＜0，点K3（0，d2）具有稳定性。考虑旅客对机场1 的需求量d1及机场1 对机场2 的竞争系数γ12的大小关系，即考虑1-γ21d1＜0 及1-γ21d1＞0 的情况。

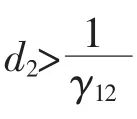
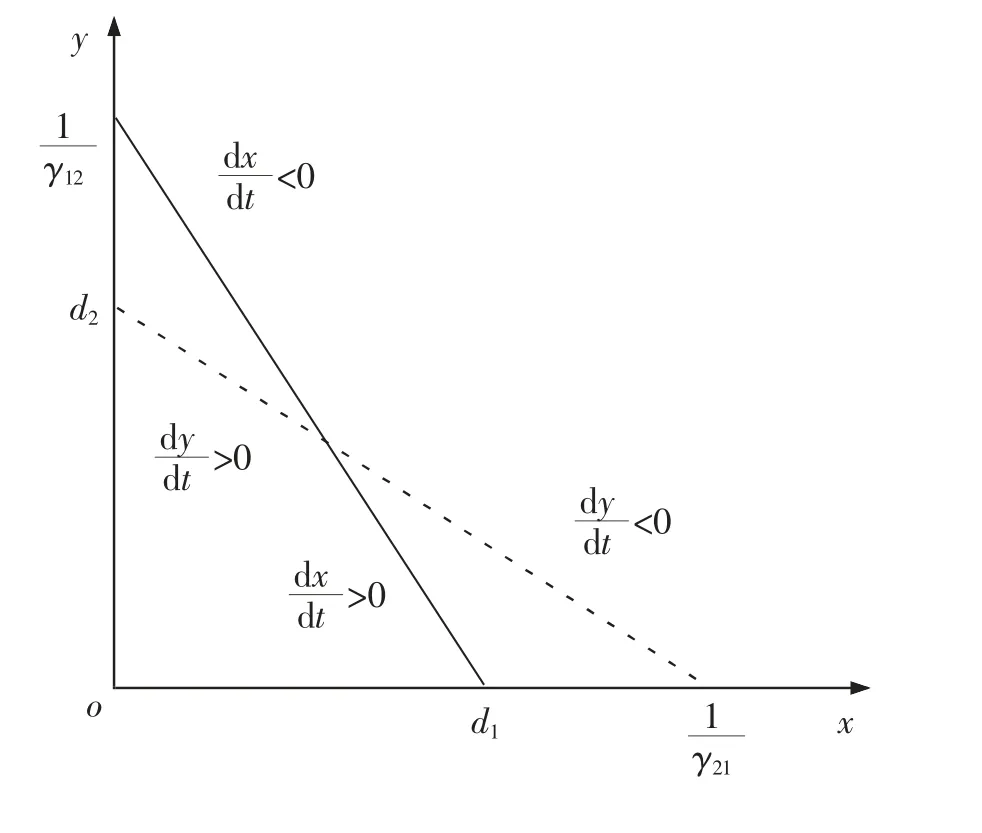
图3 条件3）时两机场竞争状态图Fig.3 The competition state diagram of two airports at Condition 3）

2 长三角机场群腹地范围测算

本文选取长三角城市群内的主要机场作为样本对象。由于上海浦东机场在长三角航空运输市场中承担大部分的国际航班，而长三角内其他机场则以国内航班为主。因此，对上海市本文仅选取上海虹桥机场作为研究对象。 最终选取的14 个机场样本如表1 所示。

由于需要通过机场辐射能力确定机场之间的腹地交叉区域，本文选择运用较为广泛的威尔逊模型，基于陈雨亭等[8]得到的综合因子得分并采用线性回归分析，将综合因子得分大于0 的机场认为是辐射能力较强的机场，得到具体的机场名称及其综合实力，如表2 所示。

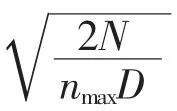
最终，各辐射能力较强的机场名称及其辐射半径如表3 所示。 根据辐射半径画出各机场的腹地范围，如图4 所示。

表1 长三角地区14 个主要机场Tab.1 14 major airports in the Yangtze river delta region

表2 辐射能力较强机场及其综合实力Tab.2 Strong radiation capacity airport and its comprehensive strength

表3 各机场辐射半径Tab.3 Radiation radius of each airport

通过对比5 个机场的辐射范围，可以发现任意两机场之间均存在腹地交叉现象，甚至还存在三机场、四机场的腹地交叉区域，机场之间已经构成了一个具有相互覆盖区域的网络。因此，腹地交叉区域应是机场竞争和协同的重点。

根据上文计算所得的各机场辐射半径，本文选取南京禄口机场及杭州萧山机场，以两机场间的腹地交叉区域为对象，研究其竞争情况和可能的均衡结果。 两机场的辐射半径分别为207.382，216.553 km，腹地范围如图5 所示，腹地交叉区域包括常州市、无锡市、苏州市、湖州市、宣城市全境及南京、杭州等市的部分区域。

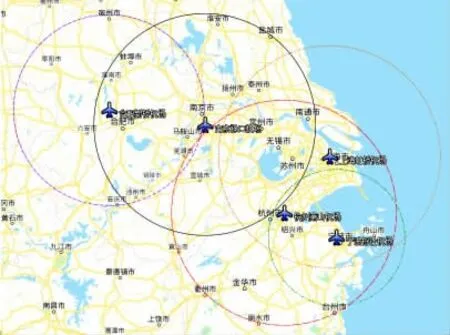
图4 各机场腹地范围图Fig.4 Hinterland map of each airport

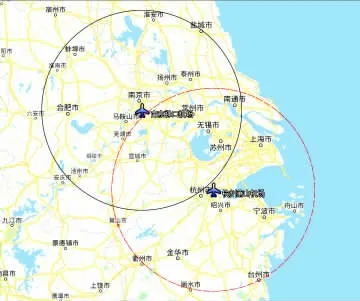
图5 南京禄口机场、杭州萧山机场腹地范围图Fig.5 Hinterland area of Nanjing Lukou Airport and Hangzhou Xiaoshan Airport

3 交叉腹地竞争均衡仿真

为了更直观地了解两机场间的竞争稳定状态及所需条件，分析参数在不同取值情况下对机场最终竞争均衡结果的影响，针对选取的南京禄口机场和杭州萧山机场，使用MATLAB 对两机场的竞争稳定状态进行仿真。

由于无法确定腹地交叉区域内两机场目前的市场份额， 本文假设两机场的初始市场份额均为50%，市场份额的变化率根据2018 年两机场旅客、货邮吞吐量的增速确定[13]，对数据进行无量纲化处理，得到两机场市场份额的变化率ρ1，ρ2为4.15，8.1。 按照第一节各平衡点的参数条件进行数值仿真，最终得到下列3 种情况。

1） 根据前文计算所得的机场综合实力，得到两机场的竞争系数γ12，γ21为0.81，1.24。 设最大需求量d1，d2均为100。 据此，两机场市场份额随时间的变化情况如图6 所示。

上述参数满足条件1-γ21d1＜0 且1-γ12d2＞0， 即腹地交叉区域内的旅客对机场1 的需求量d1大于机场1对机场2 的竞争系数γ12，且旅客对机场2 的需求量d2小于机场2 对机场1 的竞争系数γ21。

最终结果对应图2 的分析。在t=0 时，两机场拥有同样的市场份额。 但在该交点后，随着时间t 的推移， 南京禄口机场的市场份额逐渐增加，杭州萧山机场的市场份额逐渐减少。 最终，禄口机场获得全部市场份额，而萧山机场被淘汰。

2） 不改变两机场的机场综合实力，即竞争系数γ12，γ21。将最大需求量d1，d2设为100，200。据此， 两机场市场份额随时间的变化情况图7所示。

图6 两机场仿真结果1Fig.6 Simulation result 1 of two airports

上述参数满足条件1-γ21d1＜0 且1-γ12d2＜0， 即腹地交叉区域内的旅客对机场1 的需求量d1大于机场1对机场2 的竞争系数γ12，且旅客对机场2 的需求量d2大于机场2 对机场1 的竞争系数γ21。

最终结果对应图1 的分析。 随着时间的推移，南京禄口机场的市场份额逐渐增加，杭州萧山机场的市场份额在经历小段时间的增长之后开始逐渐减少。最终，仍是禄口机场获得全部市场份额，而萧山机场被淘汰。

3） 设两机场的竞争系数γ12，γ21均为1，最大需求量d1，d2均为50。 得到两机场市场份额随时间的变化情况如图8 所示。

上述参数满足条件1-γ12d2＞0 且1-γ21d1＞0， 即腹地交叉区域内的旅客对机场2 的需求量d2小于机场2对机场1 的竞争系数γ21，且旅客对机场1 的需求量d1小于机场1 对机场2 的竞争系数γ12。

最终结果对应图3 的分析。 在t=0 时，杭州萧山机场与南京禄口机场有着同样的市场份额，随着时间的增加，两机场的市场份额也随之变化，最终两机场均拥有一定的市场份额且达到均衡状态。 在该条件下，任何一个机场都不会被淘汰，两机场在竞争中实现了共存。

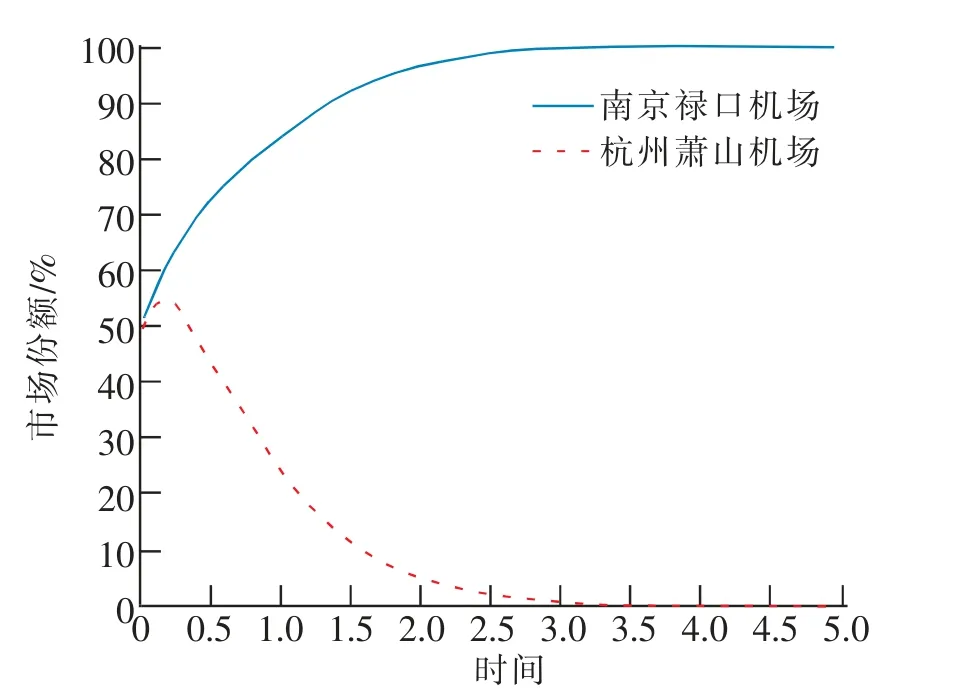
图7 两机场仿真结果2Fig.7 Simulation result 2 of two airports

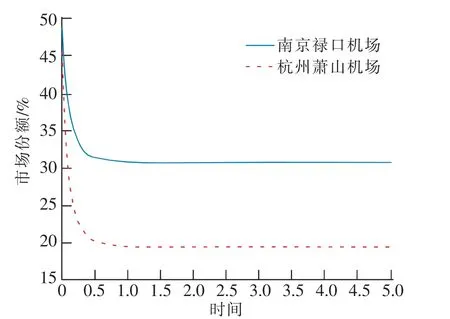
图8 两机场仿真结果3Fig.8 Simulation result 3 of two airports

4 结论

对辐射域交叉部分进行竞争均衡研究，可进一步确定影响竞争力的各类因素，进而为机场提升自身在区域多机场系统内的竞争力提供理论依据。 本文基于Lotka-Volterra 模型， 考虑机场综合实力对竞争的影响，求解区域多机场系统内两机场在腹地交叉区域的竞争均衡状态及满足条件，确定机场市场份额的变化趋势，最后对该模型进行数值仿真。

结果表明，本文建立的竞争均衡模型能较好地描述机场在辐射域交叉部分的竞争与协同态势。 机场间的竞争均衡结果随机场综合实力、腹地交叉区域旅客对机场的需求量而相应改变。 当旅客对两机场的需求量均小于本机场与另一机场综合实力的比值时，两机场将在腹地交叉区域内均占有一定的市场份额，实现了最终的竞争均衡。

同时，由于机场综合实力包含客货运吞吐量、飞机起降架次、航站楼面积等10 个指标，每一指标对机场综合实力、对辐射域交叉部分竞争均衡结果的影响及其数值关系则需要进一步研究分析。