基于深度学习的高速磁浮轨道不平顺预估
2020-07-09李东帅黄靖宇
李东帅,黄靖宇
(同济大学1. 交通运输工程学院; 2. 国家磁浮交通工程技术研究中心,上海201804)
轨道不平顺是列车振动的主要激扰源,是产生车轨间动作用力的主要原因,对列车运行的安全性、稳定性以及乘客的舒适性有着重要影响。
1 高速磁浮轨道不平顺研究方法
在目前高速磁浮的轨道不平顺测量中,采用的主要系统仍是以惯性基准法为原理设计的系统[1]。惯性基准法效率高、成本低,适用于大多数情景下的轨道不平顺测量。 然而,时瑾[2],石玉红[3]等指出,车辆振动响应与轨道不平顺之间存在滞后性,因此利用当前点的加速度计算当前位置处的轨道不平顺就不甚合理。此外,惯性基准法仅能够适用于轨道的高低不平顺,对于水平不平顺计算精度误差较大[4]。
目前,随着计算机算力的不断提升,利用惯性基准法的基本原理结合深度学习平台来研究车辆的动态响应成为了学术界研究的主流。 路天屿[5]建立了车辆轨道耦合模型,利用支持向量机算法,以车辆振动响应实现对轨道刚度突变位置的识别。史红梅[6]利用车辆轨道耦合模型,设计出一种基于车辆振动响应的轨道不平顺智能感知算法,同时考虑了几何不平顺和刚度不平顺等因素,实现了对轨道不平顺的预测。PANG X M[7]利用非线性自回归神经网络对轨道不平顺等序列类型特征的适应性,构建深度神经网络实现对轨道不平顺的预测。利用深度学习平台构建车辆振动加速度与轨道不平顺的关系未能够根本解决利用惯性基准法测量产生的根本问题,仍存在如下3 类问题:①采用单一BP 神经网络进行建模,未能充分考虑车辆在轨道不平顺激励下所产生滞后性的特点;②大多数研究是对高低不平顺进行建模,对水平不平顺研究较少;③数据量较少,BP 神经网络容易存在过拟合现象,导致神经网络泛化能力较差[8]。 基于上述因素,导致利用神经网络进行轨道不平顺预估的精度远不能够达到工程级别的要求。
本文基于车辆轨道耦合动力学理论,充分考虑车辆振动与不平顺激励的滞后性特点,对深度神经网络结构进行合理调整,构建适用于轨道高低及水平平顺状态检测的深度神经网络,基于车体动力学仿真数据验证表明,深度神经网络能够较好应用于轨道平顺状态检测场景。
2 TR08 高速磁浮车辆动力学特性分析
赵春发[9]指出,TR08 磁浮车辆结构主要包括了车体和悬浮架,悬浮架是整车的走行机构,通过空气弹簧、摇臂、摆杆、牵引拉杆等机构与车体底部连接,从而将悬浮力、导向力、牵引力和制动力通过二系悬挂系统传递给车体。 经过分析可知,TR08 型磁浮车辆各部件的自由度如表1 所示。

表1 TR08 型磁浮整车自由度Tab.1 TR08 maglev vehicle’s degree of freedom
时瑾[2],石玉红[3]等指出,车辆振动与轨道不平顺之间存在滞后效应,然而在以往的轨道不平顺预测中大多忽视了这种滞后效应所带来的影响。 如图1 所示为轨道高低不平顺示意图。
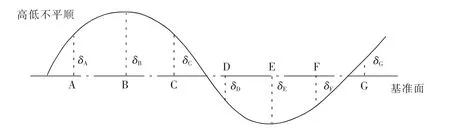
图1 轨道高低不平顺示意图Fig.1 Schematic diagram of track height irregularity
列车在G 点处的振动加速度aG不仅受G 点处的轨道不平顺δG的影响,还受G 点之前所有点的不平顺影响,如式(1)所示

式中:δi代表第i 点的轨道高低不平顺;ai代表第i 点的振动加速度。
由式(1)可得,通过振动加速度反算轨道不平顺时,某一点处的轨道不平顺,不仅与该点处的加速度有关,还与该点附近处的振动加速度有关,如式(2)所示

由此可以看出,利用传统的BP 神经网络进行轨道不平顺与列车振动响应建模,不能很好的表征这种滞后效应,而通过卷积核扫描的方式能够较好的表征这种滞后效应。 故选用CNN 网络构建深度神经网络,使其更能够符合列车真实的运行状态。
3 卷积神经网络
近年来,卷积神经网络(convolutional neural networks,CNN)凭借着其优异的性能,已经在图像理解、模式识别等领域得到了广泛的应用[10]。 与传统人工神经网络不同的是,CNN 有着权值共享以及局部连接的特点,减少了参数的数量,同时CNN 网络具有平移不变性,符合轨道不平顺预估的前提假设。CNN 网络主要包含卷积层、批量归一化(batch normalization,BN)层、激活层等结构。
3.1 CNN 的网络结构
3.1.1 卷积层
在卷积层,输入到卷积层的特征图被一个可训练的卷积核进行卷积,通过一个激活函数进行激活,可以得到输出特征图,多个卷积核可以产生多个输出特征图。 卷积层的作用在于为网络引入非线性特征,使其能够最大概率的拟合,其正向传播的公式如下

式中:ulj为卷积层l 的第j 个通道的卷积输出;f 为激活函数,作用在于为深度神经网络引入非线性因素;klij为卷积核矩阵;blj为卷积后特征图的偏置;*为卷积符号。
3.1.2 批量归一化层
在深度神经网络中,如果网络的激活函数输出很大,则相应地其梯度就变小,单次迭代造成的学习速率慢。 因此BN 的作用就是调整网络激活输出时的分布,使经过每层网络激活后的梯度能够到一个较大的范围内,加快网络的收敛速度。
批量归一化主要有以下4 个步骤:
1) 求得输出数据X 的均值μB

2) 求得输出数据的方差σB2

3) 对输出数据进行归一化

4) 给定超参数γ,β 用于调节数据分布

式中:m 代表输入批量训练中一个批量的样本数量;xi代表第i 个样本的输入值;ò 代表偏移项, 防止分母出现0,一般取0.001。
通过上述步骤,使网络能够有效调整层间数据分布,加快深度神经网络的收敛速度,同时在一定程度上缓解了过拟合现象。
3.1.3 激活层
激活层的作用在于为卷积神经网络加入非线性因素,因此激活层选用的激活函数全部为非线性激活函数,常用的激活函数有sigmoid,relu,tanh 等,为加快神经网络的收敛速度,简化神经网络的计算流程,选用relu 激活函数,其表达式如式(8)所示

从式(8)表达式可以看出,原始数据经过relu 函数激活后,数据值的分布介于[0,+∞),与高速磁浮轨道不平顺的真实数据分布相差较大,不能够很好地拟合。 因此为使神经网络的预测值能够更贴近于轨道不平顺的真实数据分布,神经网络最后两层采用自定义激活函数f(x)=5tanh(x),表达式如式(9)所示

通过自定义激活函数实现了输出值的分布介于[-5,5]之间,符合轨道不平顺的真实数据分布。
3.2 卷积神经网络的求解方法
本文选用卷积神经网络为基础理论,构建合适的网络结构,实现输入车辆的动态振动响应(包含车辆的垂向加速度,横向加速度以及速度),输出轨道不平顺(包含定子面的不平顺和导向面的不平顺)。 下面以某个1 km 长的区段为例,介绍应用卷积神经网络进行轨道不平顺预测的4 个主要步骤。
3.2.1 建立车辆-轨道耦合动力学模型
以第二节TR08 车辆自由度分析及动力学方程为基础,结合TR08 型高速磁浮列车车辆参数,利用SIMPACK 构建出TR08 型高速磁浮车辆单车体模型图,模型自由度为138,包含195 个体元、242 个力元和156个约束等元素,其中悬浮架按照弹性处理。
将实测的高低和水平不平顺数据导入,得出车体在轨道不平顺激励下的横向加速度序列ax和垂向加速度序列az。
3.2.2 数据预处理及数据增强
吴祥明[11]指出,由于乘客舒适度的影响,高速磁浮列车长时间运行的垂向加速度az和横向加速度ax应满足式(10)要求

同时,高速磁浮列车长期运行的垂向加速度应满足德国AGT 的建议值0.125 g 以内[12]。 因此,在实际建模过程中,应取车辆振动符合实际的区间段,避免在区间段内出现数据的异常值。
数据增强是深度神经网络预处理中常用的手段,用于解决数据量较少的问题,进而缓解过拟合现象的发生。 以本案例为例,可将1 km 的不平顺线路随机切分为小长度序列,可实现对样本量的扩充。
3.2.3 卷积神经网络搭建
在充分考虑到轨道不平顺与车辆振动间的非线性关系条件下, 以卷积层和批量归一化层为基础结构,分别设计了5~12 层的卷积神经网络实现对轨道不平顺的预测。 同时亦可探究轨道不平顺预测的最优网络结构。 在损失函数选择方面,由于通过车辆振动响应来对轨道不平顺进行预测本质是一个预测连续值的回归问题,故采用二阶均方差来衡量预测值和真实之间的差异,表达式如式(11)所示

式中:Yi为样本i 的轨道不平顺真实值;为样本i 的轨道不平顺预测值。
3.2.4 效果评估为了衡量深度神经网络的预测效果,采用相对精度来表征模型的预测能力。 其表达式如式(12)所示

由式(12)可知,R2的值介于[0,1],且R2越接近于1,模型越接近于真实值。
综上所述,利用卷积神经网络进行轨道不平顺预测的流程示意图如图2 所示。

图2 CNN 预测轨道不平顺流程图Fig.2 Flow chart of CNN predicted track irregularity
4 案例分析
案例以某地实测的高速磁浮轨道左右、高低不平顺数据作为输入,基于车辆轨道耦合动力学理论,利用SIMPACK 构建车轨耦合动力学模型,得到不平顺激励下的车辆动力学响应(垂向加速度,横向加速度以及速度),最终取数据较为稳定的区间段进行建模。
4.1 原始数据分析
由于列车运行初期数据波动较大,导致测量得到的轨道不平顺存在异常值,最终对数据进行合理清洗后,选取了列车运行稳定的2 km 区间段内约83 000 个采样点进行建模分析,区间段内轨道的高低不平顺及水平不平顺如图3,图4 所示。

图3 轨道高低不平顺Fig.3 Track vertical irregularity
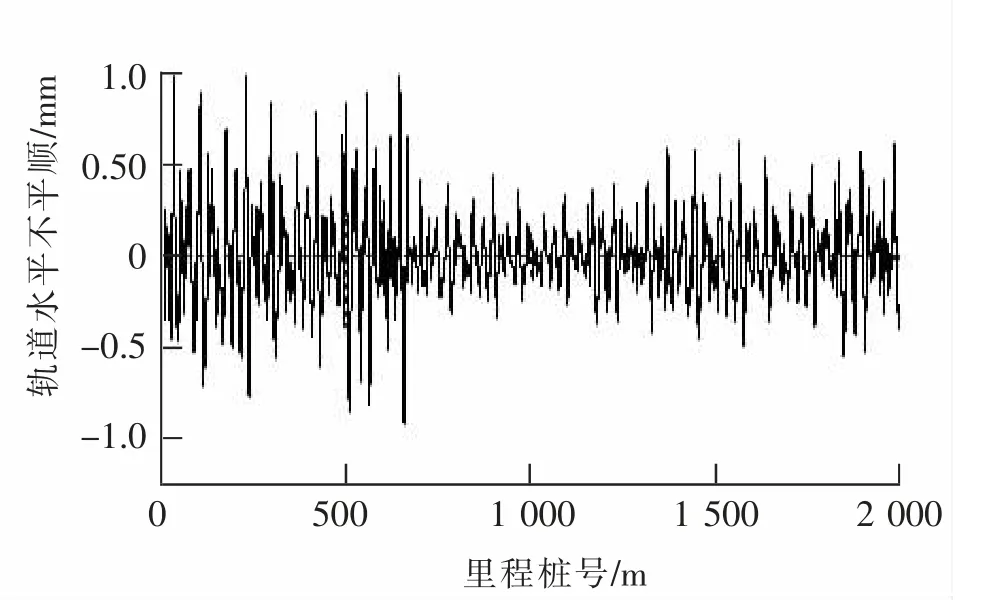
图4 轨道水平不平顺Fig.4 Track lateral irregularity
将上述不平顺输入到SIMPACK 建立的车辆轨道耦合动力学模型中,得到轨道在高低、水平不平顺激励下车辆的垂向加速度及横向加速度,如图5,图6 所示。
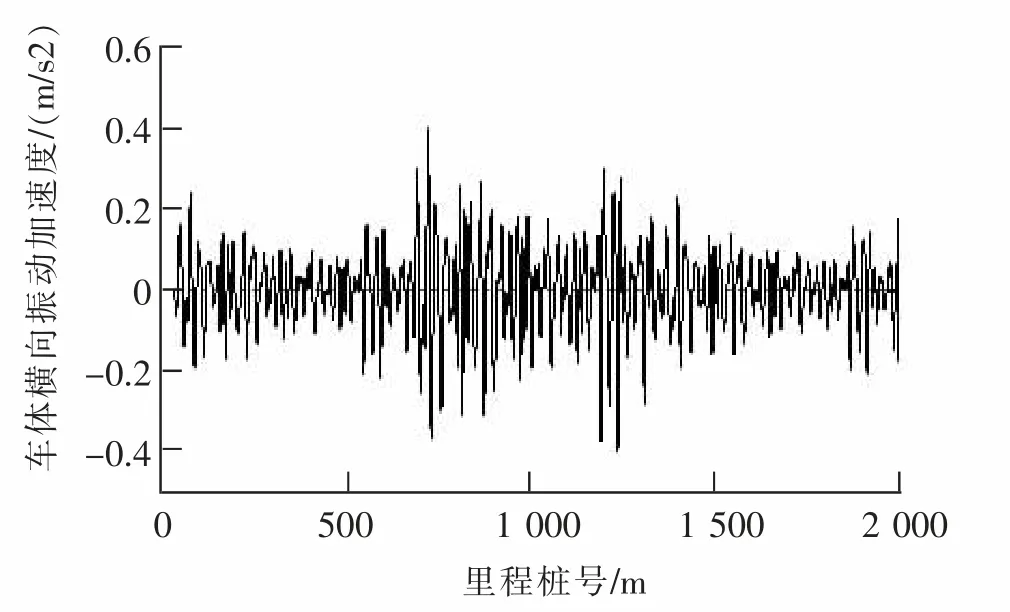
图5 车体横向加速度Fig.5 Lateral accelerationof vehicle
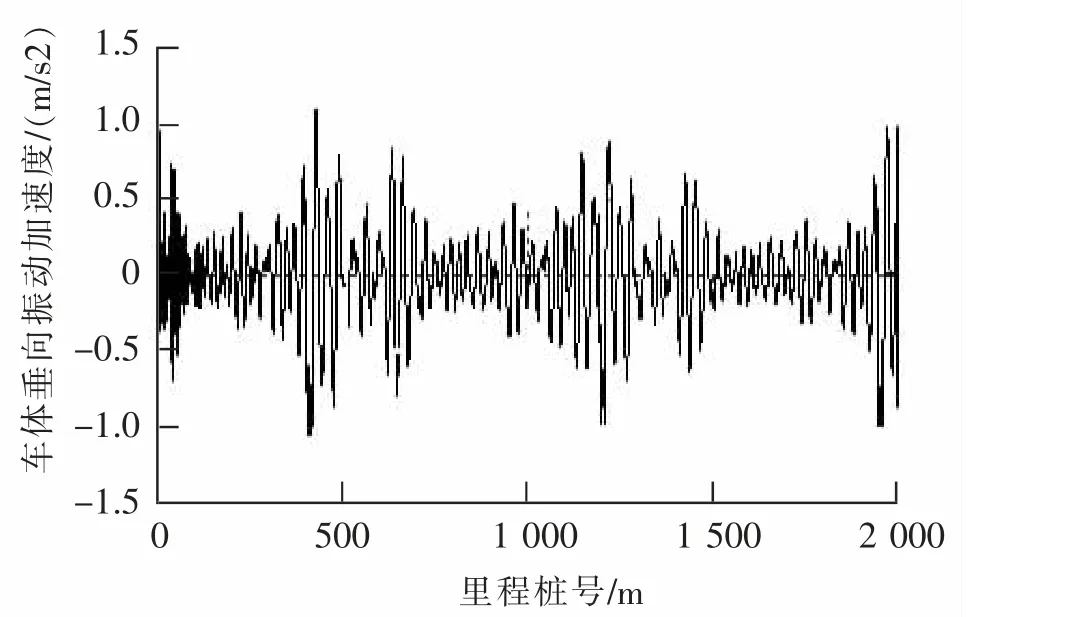
图6 车体垂向加速度Fig.6 Vertical acceleration of vehicle
为实现对神经网络的充分训练,需要进行数据增强。 将上述83 000 个采样点随机裁剪为8 000 个区间长度为10 000 的小区间(区间允许存在重叠)。 同时,对8 000 个样本进行随机划分,取6 000 个样本作为训练集对深度神经网络进行训练,取剩余2 000 个样本为测试集,用于表征深度神经网络对未知数据的预测能力,即模型的泛化性能。
4.2 深度神经网络训练过程
为探究神经网络的最优层数, 利用Google Tensor Flow 结合Python 分别构建5~12 层的卷积神经网络,输入原始数据对模型进行训练,利用Tensorboard 监控模型的训练过程。 图7 展示了不同层数下深度神经网络的迭代次数与训练集测试集精度的关系曲线,从图中可以看出:
1) 随着迭代次数的不断增加, 训练集的相对误差一直降低, 表明神经网络对训练集数据拟合越来越好;测试集的相对误差呈现先升高后降低的趋势,表明在深度神经网络训练初期,随着迭代次数的增加,模型越来越拟合数据的真实分布规律,直至测试集精度达到最高,之后随着迭代次数的增加,模型更多关注于训练集的随机误差而使得模型对未知数据的预测能力变差,此时模型认为模型达到过拟合,应停止继续训练。 定义在测试集最高点处所对应的迭代次数为神经网络的收敛点,用于表征不同层数下神经网络的收敛速度。
2) 随着网络层数的加深,神经网络的收敛点逐渐增加,由21 轮迭代后收敛逐步升高至59 轮迭代后收敛,神经网络的收敛速度越来越慢,随着网络层数的加深,深度神经网络表征非线性能力逐步增加,同时收敛速度变慢。
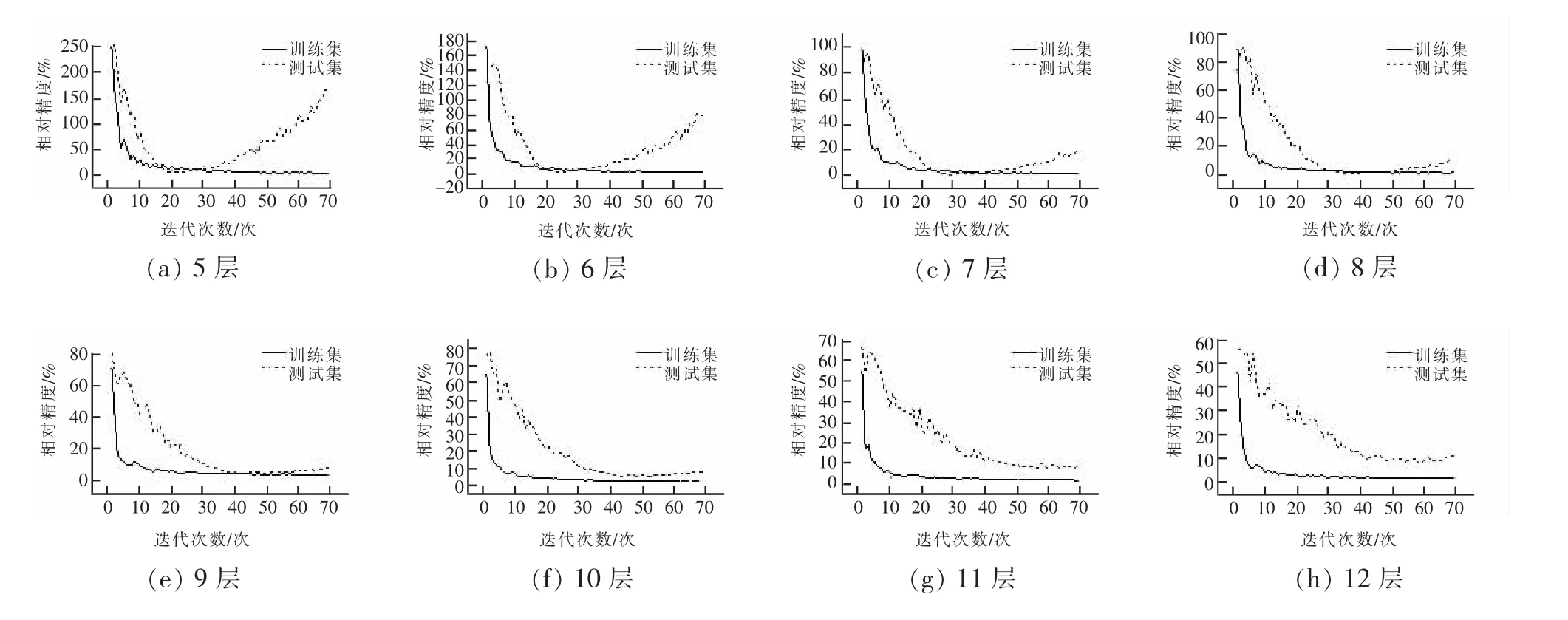
图7 不同层数下神经网络迭代次数与相对误差的训练曲线Fig.7 Training curve of iterative times and relative errors of neural network in different layers
3) 随着网络层数的加深,神经网络在训练集的初始相对误差由250.31%降低至44.81%,测试集的初始相对误差由236.90%降低至54.51%,随着网络层数的加深,深度神经网络初步迭代误差逐步降低,但同时加深迭代次数所带来的精度收益降低。 考虑到计算时长的限制,需合理控制深层神经网络的迭代次数。
4.3 结果分析
为验证不同层数的神经网络在训练集和测试集的性能表现, 在深度神经网络达到收敛点的前提下,随着网络层数的加深,神经网络在训练集和测试集的相对精度如表2 所示。
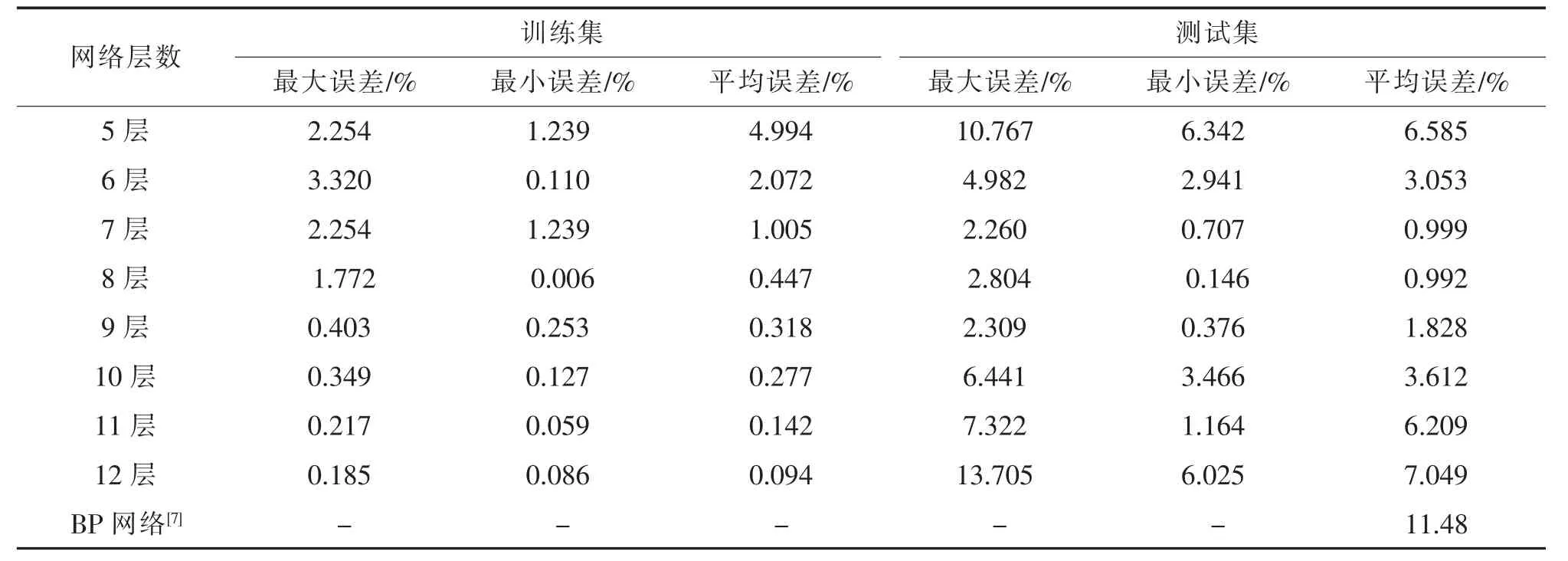
表2 不同网络结构训练测试误差表Tab.2 Training and testing error of different network structures
从表中可以得出以下结论:
1) 随着网络层数的加深,训练集的精度一直升高,说明随着网络深度的不断增加,深度神经网络表达非线性的程度越高,使得模型能够对训练集最大程度的拟合;
2) 随着网络层数的加深,测试集的精度呈现着先升高后降低的趋势,说明起初深度神经网络层数的加深使得模型的泛化性能和拟合程度有着明显的提高,之后随着深度神经网络层数的增加,拟合程度虽然进一步提高,但是模型的泛化性能变差,此时出现了过拟合的现象。
综上所述,深度神经网络的最优层数为8 层,在8 层神经网络在训练集和测试集上的精度达到最高。 为直观表征神经网络的泛化性能,在测试集上随机抽取一个长度为10 000 的样本,测试8 层深度神经网络未参与训练的样本下的性能,用于验证该结论的普遍性,作为对比,依据PANG X M[7]的结构方案训练双层BP神经网络,在同等样本下对比两者的预测效果。
从图8 及表3 中可以看出:
1) 从整体图像看,双层BP 神经网络和CNN 网络均能够较为准确地实现对轨道不平顺的预测,精度均超过80%,均可实现对轨道不平顺的定性预测;
2) 从局部放大图可以看出,双层BP 神经网络明显存在着线性程度不够的问题,在不平顺波动较大的区间段往往会采用低阶多项式曲线的策略进行处理,误差较大。 8 层CNN 由于层数较深,能够比双层BP 神经网络有更强的非线性预测的能力,因此对于不平顺波动较大的区间预测程度较好;
3) 从单个样本来看,CNN 在水平不平顺的预测精度略好于在高低不平顺的预测精度,同时远好于双层BP 神经网络的拟合程度。 这与表2 所得出的结论一致。
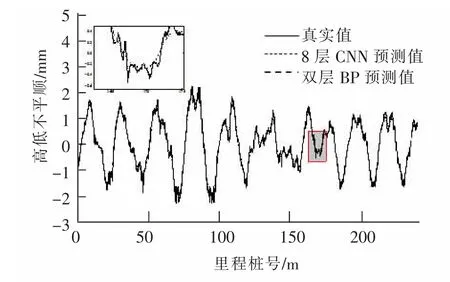
图8 高低不平顺的真实值与预测值对比图Fig.8 Comparison between real value and predicted value of vertical irregularity
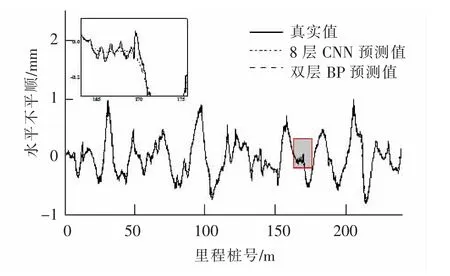
图9 水平不平顺的真实值与预测值对比图Fig.9 Comparison between real value and predicted value of lateral irregularity
分别计算CNN 模型预测值和BP 模型预测值的相对精度R2,如表3 所示。

表3 不同网络结构预测精度表Tab.3 Prediction accuracy of different network structures
结合表2、 表3 以及图9 可以看出,8 层CNN 在训练集的平均误差为0.447%, 在测试集的平均误差为0.992%,同时为了表征模型的泛化性能,在为参与训练的测试集中抽取一个样本进行测试。 发现8 层CNN在高低不平顺的测试精度为0.988 2,在水平不平顺的测试精度为0.990 7,可以看出,模型在未知数据集下的训练效果良好,证明试验所得出的结论具有普遍性,符合高速磁浮轨道不平顺的测量精度要求。
5 结论
本文的主要结论如下:
1) 本文提出了一种新型的测量轨道不平顺的方案,通过测量车辆加速度,构建CNN 实现对轨道不平顺的检测,克服了传统的惯性基准法只能够测量高低不平顺的缺点,实现了对高低不平顺和水平不平顺的精细化测量;
2) 与目前主流的BP 神经网络测量轨道不平顺方案相比, 本文提出的CNN 无论是对训练集的拟合程度还是对未知数据的预测能力上均表现较好,相较于BP 神经网络有大幅度提升;
3) 使用CNN 实现对轨道不平顺测量的方案考虑了轨道不平顺对振动加速度影响的滞后性,实现了对轨道不平顺的精细化测量, 实验结果证明,8 层CNN 网络能够较为合理的表征轨道不平顺与车辆振动相应的关系,测试集精度高达99%以上。
