基于小波包分解和支持向量机的局部放电识别方法研究
2020-07-09姜伊欣娄雨靖
陈 峰,姜伊欣,娄雨靖
(1.国网浙江杭州市余杭区供电有限公司,浙江 杭州 310012;2.杭州电子科技大学,浙江 杭州 310018)
0 引言
10 kV 配电线路是电力系统中主要线路之一,其开关设备质量性能对整个电网系统运行存在较大影响[1]。局部放电的超声波检测法是基于局部放电现象发生时产生机械信号的原理提出来的,超声波信号检测具有较好的抗电磁干扰能力,易于实现在线检测和空间定位。同时,超声波检测方法也有分类识别局部放电的潜力,便于更进一步实现绝缘状态的细致评估[2]。因此,目前主要使用超声波探头采集局部放电信号进行分析。
如何从非平稳的超声信号中提取出特性信息是判断开关柜有无局部放电及局部放电类型的关键。传统的特征提取方法主要包括时域上的波形结构特征提取、频域上的谱估计特征提取、时频分析中的短时傅里叶变换等方法。由于局部放电信号的非线性、非平稳性和较强的时变性,传统的特征值提取方法在处理此类信号时有一定的局限性。如傅里叶变换分析方法在变换时丢掉了时间信息,无法判断一个特定信号的发生时间[3]。小波变换虽然能较好地分析局部放电信号的时频特性,但过分依赖小波基的选取,而且小波基长度有限,处理时会产生能量泄漏,因而难以对信号进行精准时频分析[4]。由于小波变换在分解的过程中只对低频信号再分解,对高频信号不再实施分解,使得频率分辨率随频率升高而降低。在这种情况下,小波包分解应运而生,它不仅对低频部分进行分解,对高频部分也实施了分解,而且小波包分解能根据信号特性和分析要求自适应地选择相应频带与信号频谱相匹配,是一种比小波分解更为精细的分解方法[3]。因此,本文运用小波包分解方法对局部放电信号进行处理分析。
在局部放电分类算法方面,主要有贝叶斯决策法[5]、决策树法[6]、随机森林[7-8]、人工神经网络法[9]和支持向量机法(SVM)[10-12]等。将小波包分解方法结合SVM 技术(SVM-Wavelet)应用到开关柜超声局部放电信号的识别分类中,运用小波阈值分析法对采集的开关柜超声局部放电信号进行去噪处理,再利用小波包分解方法对消噪信号进行分解,信号经过小波包分解后得到若干个小波包分解系数,然后提取小波包分解系数的能量,得到小波包节点能量特征向量,最后运用SVM 作为决策分类器来识别信号的局部放电类型。
1 基于SVM-Wavelet 的开关柜局部放电信号识别方法

图1 基于SVM-Wavelet 的开关柜局部放电信号识别流程
基于SVM-Wavelet 的开关柜局部放电信号识别的实现流程如图1 所示,首先对采集的开关柜局部放电信号进行小波包分解,分解后对得到的小波包分解系数进行特征提取,最后使用SVM 对开关柜局部放电信号进行分类识别。
1.1 小波包分解
小波分析是一种时频域的分析方法,在分析非线性的平稳信号过程中十分具有优势[13]。以小波包3 层分解为例,其分解结构如图2 所示。信号经过小波包分解后得到近似信号的细节信号,之后在第2层再对近似信号和细节信号再分解。

图2 小波包分解结构
设原始信号S 为(0,0)节点,(1,0)表示第1 层小波包分解的低频系数S10,(1,1) 表示第1 层小波包分解的高频系数S11,再对S10和S11进行分解。分解S10,(2,0)表示第2层小波包分解的低频系数S20,(2,1)表示第2 层小波包分解的高频系数S21;分解S11,(2,2)表示第2 层小波包分解的低频系数S22,(2,3)表示第2 层小波包分解的高频系数S23,以此类推得到各个节点表示的含义。
S 信号3 层小波包分解具有如下含义:
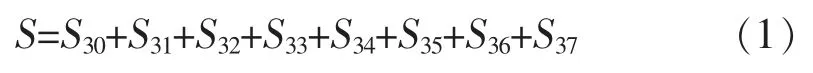
小波包分解的层数影响着局部放电信号的时频分析精度。若提高分解层数,那么信号频带分辨率也提高,反之信号频带分辨率就相应减少,分析速度加快。若信号的采样频率为f,经过i 层小波包分解,信号被划分到2i个频带上,其中第j 个频带频率范围为
1.2 开关柜超声局部放电信号的小波阈值去噪
在对开关柜超声局部放电信号采集的过程中,由于现场的环境条件多变,采集到的局部放电信号的噪声干扰较多,会影响局部放电信号识别分类的准确性。针对局部放电信号检测中出现的噪声干扰问题,使用小波阈值分析法对信号进行分析处理。小波阈值去噪基本过程如图3 所示。

图3 小波阈值去噪基本过程
1)小波基函数的选择。
对信号进行小波分析过程中,小波基函数的选取是非常重要的。与傅里叶分析不同,小波分析的基函数不是唯一的,常用的小波基函数包括Haar 小波、Daubechies 系列小波、SymletsA 系列小波等,选取不同的小波基函数会导致去噪效果的不同。研究发现Daubechies(DB)系列小波具有紧支性且是正交小波基,非常适合处理突变信号,而且文献[3]使用DB6 小波基对局部放电信号进行去噪,取得的效果比较理想。因此,选取DB 系列中的DB6 小波基作为去噪的基函数。
2)阈值和阈值函数的选择。
设w 为小波系数,T 为阈值门限,sign()为符号函数,常见的阈值函数有硬阈值函数和软阈值函数,分别如式(1)和式(2)所示。

软阈值函数和硬阈值函数虽然对信号的去噪取得了一定的效果,但它们仍然存在着缺陷[14]。可选取Birge-Massart 处罚算法获取去噪的阈值门限。
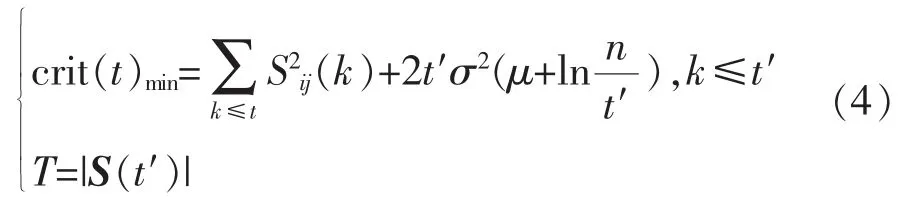
式中:crit 为熵名;t′为crit(t)取最小值的解;Sij为按绝对值从大到小排列的小波包系数,k≤t,t=1,2,…n;σ 为噪声标准差;n 为系数的个数;μ 是用于处罚的调整参数(必须大于1);S(t′)为Sij(t′)组成的矩阵。
1.3 开关柜超声局部放电信号特征构造
在整个开关柜局部放电超声信号分类识别的体系中,最重要的环节就是局部放电信息的特征提取。当开关柜发生不同的局部放电时,局部放电信号中频率分布会发生改变,能量分布也会发生改变。局部放电信号经过小波包分解得到的小波包分解系数代表了信号从高到低不同频段的成分。因此,根据各个小波包分解系数的能量变化进行局部放电类型的分析。将各个小波包分解系数进行能量特征提取,具体步骤如下。
1)对信号S 进行i 层小波包分解,其中Sij为第i层第j+1 个分解节点的系数,根据式(5)计算Sij的能量。
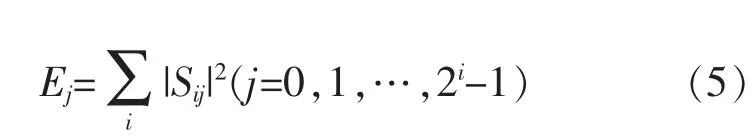
1.4 基于SVM 模型的分类方法
SVM 是一种基于统计学习理论的机器学习方法,由Vapnik 等人在20 世纪90 年代提出。这是一种基于统计学习理论为基础的机器学习算法,对非线性问题具有较强的拟合能力,并被广泛应用于时间序列预测、模式识别和系统控制等领域,是一种有效的人工智能模型。SVM 构造一个最优分类超平面,此超平面将两类样本无错误地分开且分类间隔达到最大值,以此实现样本的分类。
对于确定的样本观测集A={(x1,y1),…,(xl,yl)},特征向量xi∈Rn,样本的类标记yi∈{-1,1}(i=1,2,…,l),l 为样本个数,分类的本质就是寻找到能将正负两类完全分开的超平面。构造其分类模型如式(6)所示,其具体推导过程可参考文献[15]。
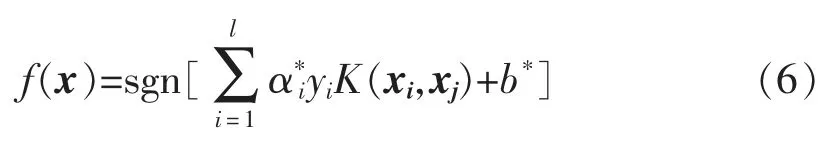
2 分类试验
选取某电子研究所研发的开关柜局部放电故障模拟实验装置采集数据。利用超声波传感器和示波器采集并储存电晕放电和悬浮放电信号,采样频率为500 kHz,各得100 组数据。
首先对原始信号进行小波阈值去噪处理,得到一系列消噪后的信号,如图4—图5 所示。
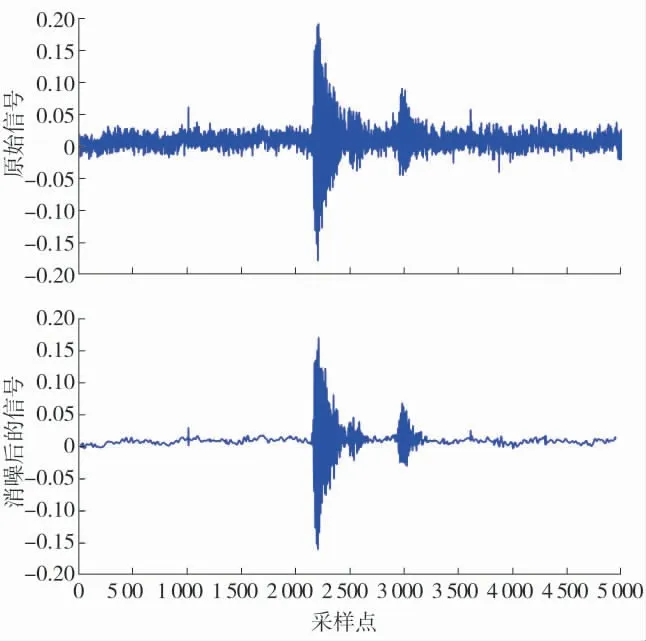
图4 电晕放电信号的小波阈值去噪

图5 悬浮放电信号的小波阈值去噪
选取DB6 小波基函数,对去噪后的局部放电信号进行4 层的小波包分解,分解后第4 层的各个节点波形的频带约为16 kHz。小波包分析得到的部分波形如图6—图7 所示。
局部放电信号经过小波包的分解和重构,得到了不同频带的信号波形。将小波包分解结果提取能量信息组成特征向量,得到200 组小波包能量特征向量。2 种放电类型各随机抽取40 组作为训练样本,剩余的120 组作为测试样本。
经测试,当非负惩罚因子C 为5.278,核函数参数g 为0.10882 时,分类准确率最高,达到了100%。将最优C 和g 代入到SVM 分类模型中,对局部放电信号进行分类识别。将SVM-Wavelet 算法与基于EMD 分解的识别方法,以及粒子群和遗传算法参数优化的方法进行比较,测试结果如表1 所示,电晕放电和悬浮放电的标签分别为0 和1,可以看出,SVM 对测试样本的分类识别正确率很高,这说明基于小波包能量谱进行局部放电信号识别的方法是有效的。

图6 电晕放电的小波包分解重构
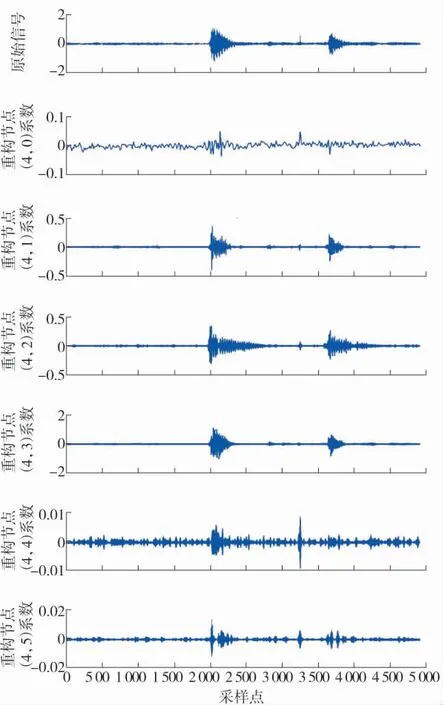
图7 悬浮放电的小波包分解重构

表1 SVM 参数寻优结果和局部放电类型识别准确率
3 结语
运用小波阈值分析法对开关柜超声局部放电信号进行去噪处理,运用小波包分析方法对消噪信号进行分解,将分解得到小波包系数提取能量特征作为特征向量,运用SVM 进行局部放电信号的分类识别,这种方法能较好地识别局部放电信号的类型。结果表明小波包分析方法能很好地处理非线性、非平稳的局部放电信号,基于SVM-Wavelet 的方法可以准确地识别局部放电类型。
