永磁同步电机神经网络速度控制器设计

田 雨，康尔良

(哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080)

0 引 言

永磁同步电机(以下简称PMSM)具有结构简单、运行可靠、体积小、效率高、高功率密度[1-2]等优点，在新能源汽车、航空航天、工业自动化等领域有着广泛的应用前景。PMSM本身是一个非线性、多变量、强耦合[3]的控制系统。传统的PID控制器结构简单，参数固定，难以满足非线性系统的高精度控制要求[4]。近年来，在矢量控制和直接转矩控制的基础上，各种非线性控制方法被广泛应用在PMSM的控制系统中，包括自抗扰控制[5]、滑模变结构控制[6]、预测控制[7]和神经网络控制[8]等。

其中，神经网络控制不依赖于被控对象的数学模型，具有自适应能力，可降低扰动和参数变化对控制系统带来的影响，受到广泛应用。文献[9]应用BP神经网络与PID控制器相结合，构建了用于调整PID控制器参数的BP神经网络模型。但是，最后实验结果表明，BP神经网络训练速度慢、泛化能力差，难以满足控制要求。文献[10]应用学习能力强的径向基函数(以下简称RBF)神经网络进行控制器参数整定。但是，没有对RBF神经网络中参数进行考虑，会降低系统的逼近能力。

本文将传统PID控制与具有强自适应、自学习能力的RBF神经网络相结合，设计一种PMSM神经网络速度控制器。用RBF神经网络自适应整定PID速度控制器参数，提高系统鲁棒性和控制精度。针对神经网络初始隐节点数难以确定的问题，通过改进资源分配网络进行离线训练，得到隐节点数，提高RBF神经网络的运算速度。

1 PMSM数学模型

在PMSM磁路线性、忽略铁心饱和等条件下，建立同步旋转坐标系下的电压方程：

(1)

式中：Rs为电机定子电阻；uq，ud，id，iq分别为d,q轴电压、电流分量；ψd，ψq为d，q轴磁链；ωr为转子电角速度。

磁链方程：

(2)

式中：Ld，Lq为d，q电感；ψf为永磁体磁通。

电磁转矩方程：

Te=p(ψdiq-ψqid)

(3)

式中：p为转子极对数。

机械运动方程：

(4)

式中：TL为负载转矩；J为转子转动惯量；B为摩擦系数。

2 PMSM速度控制器

2.1 神经网络速度控制器

采用RBF神经网络对PID参数进行自适应整定，原理框图如图1所示。

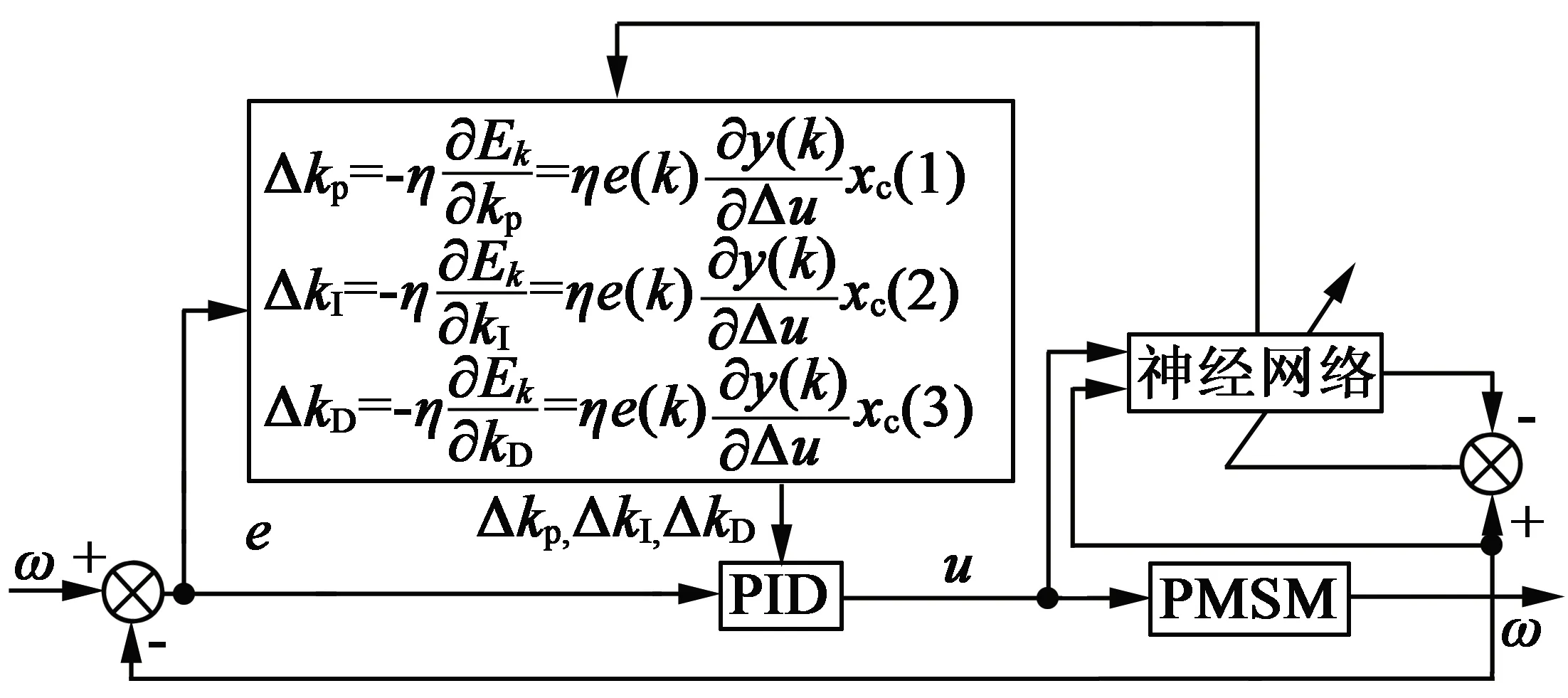
图1 自适应整定原理框图

本文采用了增量式PID控制算法，控制器的控制误差:

e(k)=ω*(k)-ω(k)

(5)

神经网络的性能指标函数：

(6)

增量式PID控制算法的三个输入:

(7)

控制器的输出：

Δiq(k)=kP[e(k)-e(k-1)]+kIe(k)+

kD[e(k)-2e(k-1)+e(k-2)]

(8)

采用梯度下降法，得到kp,kI,kD的调整量，分别如下:

(9)

(10)

(11)

2.2 RBF神经网络算法

为精确调整ΔkP，ΔkI，ΔkD，保证系统在最佳状态下运行，设计RBF神经网络算法，提供雅克比信息，对控制器参数进行自适应整定。

RBF网络结构有三层，分别为输入层、隐含层和输出层[9]。输入层到隐含层之间非线性连接，隐含层到输出层通过输出权值程线性连接[11]。RBF神经网络结构如图2所示。

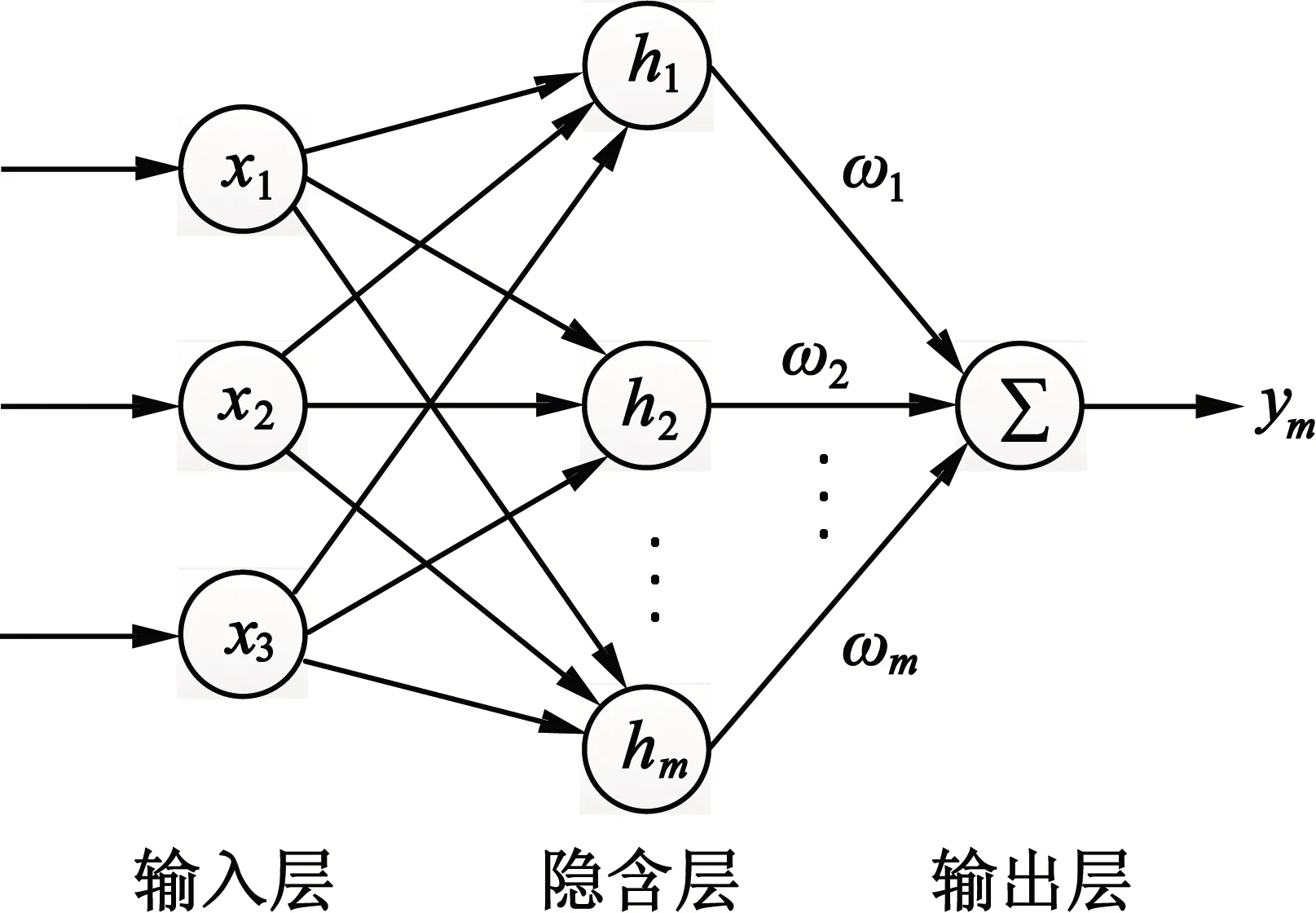
图2 RBF神经网络结构

图2中，x=[x1，x2，x3]T为网络的信号源输入。h=[h1,h2,…,hm]T为隐含层的RBF，采用高斯函数，其表达式如下：

(12)

式中：第j个隐节点的中心矢量cj=[cj1，cj2，cj3]T，bj为隐含层第j个神经元的高斯奇函数的宽度。

RBF网络输出权值：

W=[w1,…,wm]T

(13)

RBF网络输出:

ym=wTh=w1h1+w2h2+…+wmhm

(14)

RBF网络性能指标函数:

(15)

根据梯度下降法对输出权值、数据中心和基宽进行更新：

(16)

(17)

(18)

式中：k为运算次数；η为学习速率；α为动量系数。

雅克比(Jacobian)算法：

(19)

3 改进资源分配网络

构建RBF神经网络的关键在于隐节点数的确定，隐节点数过多，增加系统复杂程度，计算时间长；隐节点数过少将无法对非线性系统进行准确描述。本文采用改进资源分配网络(以下简称IRAN)方法，对神经网络进行离线训练，得到隐节点数，优化神经网络性能。

训练过程中，一般将初始节点数设为0，通过“新颖性”准则，不断对隐节点数进行调整。

RAN学习算法“新颖性”准则：

(20)

E(i)=‖y(i)-yL(i)‖>ε

(21)

式中：dj为距离准则，E(i)为误差准则。δ(i),ε分别为距离分辨率和误差精度。当新输入的样本满足“新颖性”准则时，网络中增加新的节点。不满足条件时，则通过梯度下降法对数据中心和输出权值进行调整，逐步消除误差。

因受到输入样本数据的影响，学习样本的鲁棒性较差。随着学习的不断进行，隐节点数不断增加，且增加之后不能及时删除，使网络的结构变得复杂，中间许多节点可能是无用的或冗余的。

对RAN学习算法进行改进，引入了滑动窗口的概念。“新颖性”准则增加新的条件：

(22)

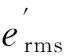
在利用梯度下降法进行数据中心和输出权值的微调时[9]，可能出现两个或多个隐节点的数据中心和输出权值都比较接近的情况，则应进行合并。

‖ci-cj‖<Δcmin

(23)

|ri-rj|<Δrmin

(24)

式中：Δcmin,Δrmin分别为数值中心和基宽的阈值，当满足条件时，将j节点合并到i节点。

wi1=wi+wj

(25)

(26)

式中：wi1，ci1为隐节点合并后的输出权值和数据中心。

随着数据中心和基宽的不断调节，会使一些隐节点远离工作区域。当多个样本输入都不在触发该隐节点时，则删除该节点。

count>Cmax

(27)

式中：count为距上一次触发隐节点后，样本输入的累计值；Cmax为进行删除的最大值。

对电机的电流和速度进行采样，作为训练样本，共1 200组数据，其中800数据作为离线训练的训练样本，400数据作为测试样本对网络进行测试。

在网络的学习训练过程中，记录归一化误差RSME和隐含层节点数的变化情况，其中：

(28)

式中：ei为第i个测试样本的误差。

IRAN测试过程中，隐节点数变化及误差精度变化曲线如图3所示。

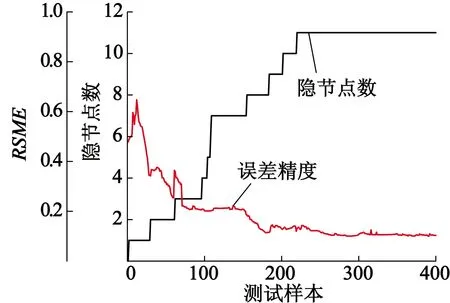
图3 隐节点数、RMSE变化图

测试过程中，随着测试样本的不断增加，隐节点数增加，在200个样本后，隐节点数稳定在11。测试网络的实际输出与期望输出之间的误差变化，随着样本的增加逐渐减小，最终稳定在0.1左右，在很小的范围内稳定波动。

4 仿真验证

在MATLAB/Simulink仿真环境中，搭建基于RBF神经网络的PMSM矢量控制系统[12]仿真模型。仿真用表贴式PMSM参数如表1所示。

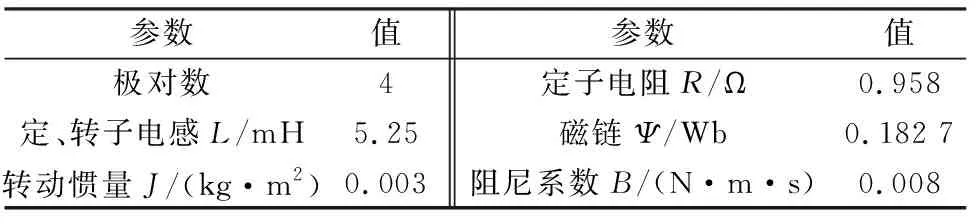
表1 电机参数

RBF神经网络无法用传递函数表示，算法由S函数和外部延时环节实现。RBF神经网络模块如图4所示。

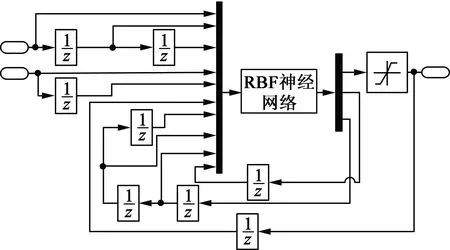
图4 基于S函数的子系统仿真模块

为说明神经网络控制器的有效性，将基于RBF神经网络速度控制器的PMSM控制系统与基于传统PID控制器的控制系统进行对比仿真。

图5中，电机空载起动，给定速度为1000r/min，在0.1s时，电机突加10N·m负载。由速度响应曲线可以看出，传统PID控制器在突加负载后，电机转速下降明显，达到稳定运行状态所需时间较长。与PID控制相比，RBF神经网络自适应控制系统在突加负载后，转速波动小、运行平稳、快速恢复到给定转速，具有更好的鲁棒性。

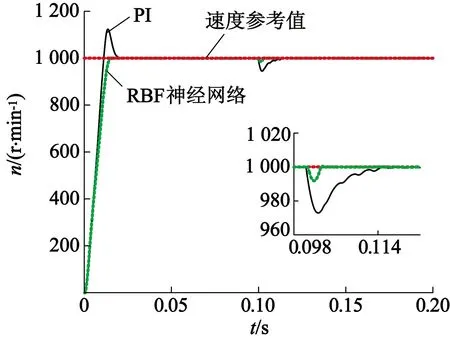
图5 负载变化时速度响应曲线

图6中，电机负载转矩2N·m保持衡定，电机的初始给定速度为600r/min，0.1s时电机速度阶跃为1 000r/min，由传统PID控制和RBF神经网络自适应控制的速度响应曲线图对比可见，基于RBF神经网络的自适应控制器在转速突变后，能够快速响应，且无超调，转速波动较小。

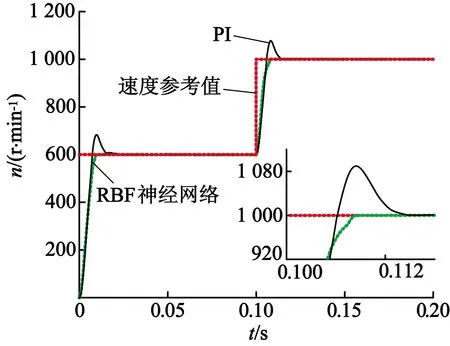
图6 转速变化时速度响应曲线

仿真结果表明，神经网络速度控制器可以快速跟踪转速变化，同时具有良好的鲁棒性。

5 结 语

本文将RBF神经网络算法与传统PID控制器相结合，利用RBF神经网络的自适应、自学习能力，在线整定PID控制器参数。并且利用IRAN算法和梯度下降法，对神经网络进行训练，得到结构简单且运算速度快的网络结构。

仿真结果表明，与传统PID控制器相比，该控制器解决了传统PID控制器因参数调节困难而无法满足PMSM控制系统高性能调速的问题，具有更高的控制精度，更好的调速性能和鲁棒性。