基于扩张状态观测器的无传感永磁同步电机研究
2020-07-09卢青高唐春茂王会明李清都
卢青高,唐春茂,王会明,李清都
(重庆邮电大学,重庆 400065)
0 引 言
永磁同步电机(以下简称PMSM)因具有结构简单、功率密度高、控制性能好、噪声低、寿命长的优点,而被广泛应用于数控机床、机器人、航空航天等领域[1-2]。在实际应用中通常采用矢量控制的方法对PMSM进行控制,利用坐标变换技术把定子电流分解为定子电流转矩分量(q轴电流分量)和定子电流励磁分量(d轴电流分量)。由于转子磁链幅值保持不变,只要定子d轴电流分量的方向与转子永磁体磁链方向保持一致就能实现解耦控制,所以系统需要获得转子磁链的位置。传统的方式是通过电机转子轴向安装机械式位置传感器,来获取转子位置信息。这会增加电机转轴上的转动惯量,加大了电机的空间尺寸和体积,降低了系统的可靠性。因此,对无传感器的PMSM矢量控制系统的研究具有较大意义[3-4]。
针对PMSM无传感器矢量控制,国内外学者经过大量研究,提出了各种解决方案[5-7],其中基于各种观测器模型的闭环算法是研究的热点之一。文献[8]提出一种全阶的滑模观测器,并加入饱和函数来减弱高频切换引起的抖振。滑模观测器方法需要用低通滤波器提取感应电动势信号,这会带来原信号幅值和相位的变化。文献[9-10]采用新型滑模观测器对反电动势进行估计,为得到平滑感应电动势,对估算的感应电动势进行了滤波处理,对滤波后估算角延时问题进行了补偿,并对抖振问题做了相关处理,使PMSM稳定带载运行。文献[11]采用了降阶观测器,起动阶段采用开环控制,采用平滑的方式进行低速与高速切换,并应用观测器进行转子速度观测,具有较强的实用性。文献[12]设计了一种三阶扩张状态观测器,提高了估计值的精度,抑制了微分峰值的现象,但是观测器阶数较高,设计复杂,从而增大了计算量。文献[13]分析了一阶线性状态观测器具有的收敛速度慢、动态响应慢,抗干扰能力差等特点,将PMSM的反电动势扩展为新状态,设计二阶状态观测器,提高了观测精度及抗扰能力,实现了扩张状态观测器对无传感器PMSM的控制,但是所设计的扩张状态观测器是线性状态观测器,需要较高的增益。文献[14]针对有位置传感器PMSM的d,q轴电流,利用扩张状态观测器对总干扰进行观测,计算出扰动前馈补偿和误差反馈律相结合的复合控制器,提高了PMSM的控制精度。
本文研究无传感器PMSM控制问题,将包含转子位置与速度信息的感应电动势扩张为新的状态,采用二阶非线性扩张状态观测器对感应电动势进行观测,从而获取转子的位置与速度信息;同时,对系统稳定性与稳态误差进行了分析。该方法增益小,无抖振,观测精度较高。仿真验证了本文方法的可行性,并获得较好的估计精度与控制效果。
1 PMSM数学模型
本文以表贴式三相PMSM为研究对象,其在α,β坐标系下的电压方程:
(1)
(2)
式中:uα,uβ为定子电压在α,β轴的分量;eα,eβ为α,β轴的感应电动势;iα,iβ为定子电流在α,β轴的分量;Rs,Ls为定子电阻,定子电感;ψf,ke为转子磁链,感应电动势系数;ωe,θe为转子电角速度,转子电角度。
从式(2)中可以看出,eα,eβ中包含了转子位置和速度信息。由于α,β轴的感应电动势无法直接测量,但是转子位置信息又是对无传感器PMSM控制的必要条件,所以需要通过一定的算法来估计感应电动势。本文通过建立二阶非线性扩张状态观测器来估计感应电动势的值,然后从中解算出转子的位置和速度信息。
2 扩张状态观测器设计过程
2.1 扩张状态观测器的原理
对于如下形式的系统[15]:
x(n)=f[x,…,x(n-1),t]+bu(t)
(3)

式(3)则可写为:
(4)
对于未知函数f(x1,x2,…,xn,t),把其扩张为新的状态变量xn+1,令xn+1=f(x1,x2,…,xn,t),此时则可构造出扩张状态观测器(以下简称ESO):
(5)
式中:e(t)=z1-x1,若非线性连续函数满足[15]:e=0,gi(e)=0,∀e1≠0,fal(0,ai,δ)≠0且当egi(e)>0,则z1,…,zn+1能够对x1,…,xn+1进行观测。
2.2 ESO在PMSM中的应用
由于eα,eβ中包含了转子位置和速度信息,为了能够对PMSM进行精准控制,可将α,β的感应电动势作为扩张的状态x2,即x2=f(x1,t)=[-keeα-keeβ]T,则可建立ESO进行观测。令:
则可将式(1)扩张为如下形式:
(6)
由此建立ESO[16]:
(7)
式中:z1对x1进行观测;z2对x2进行观测;β1为电流输出误差反馈增益;β2为感应电动势输出误差反馈增益。
为提高观测精度,可选取:g1=g2=fal(e1,ai,δ)建立非线性ESO:
(8)
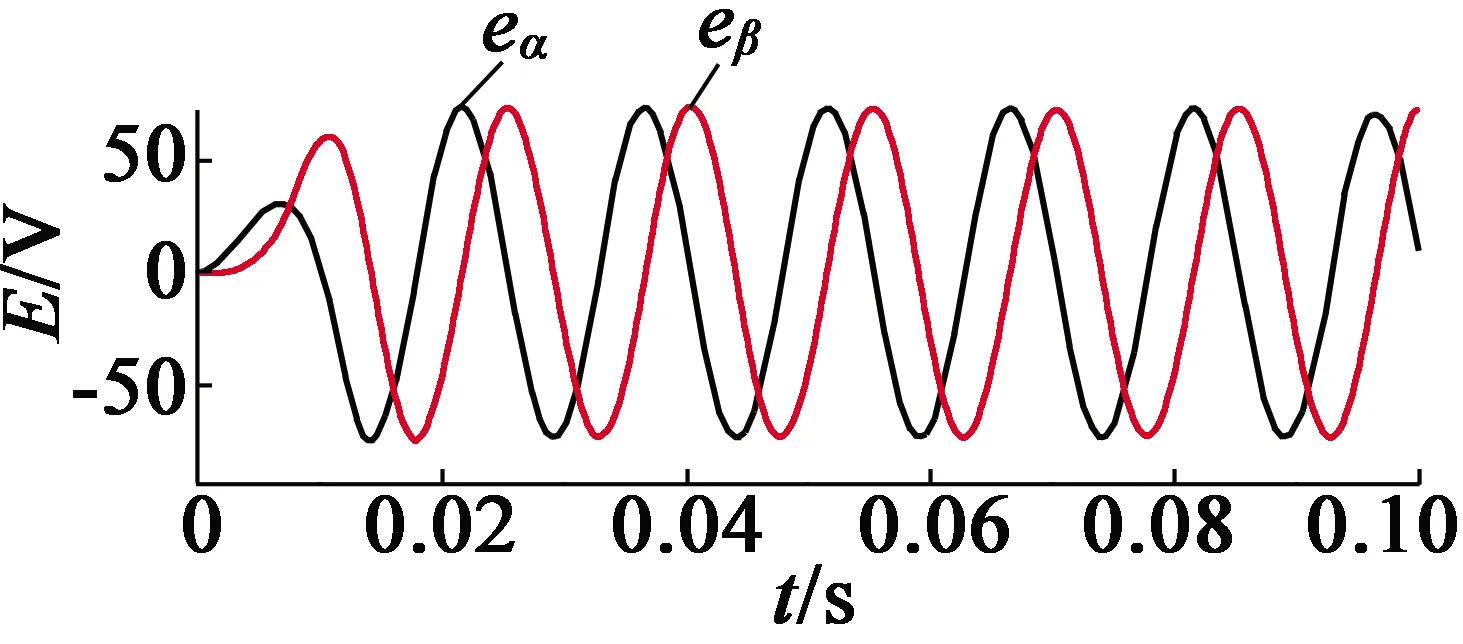
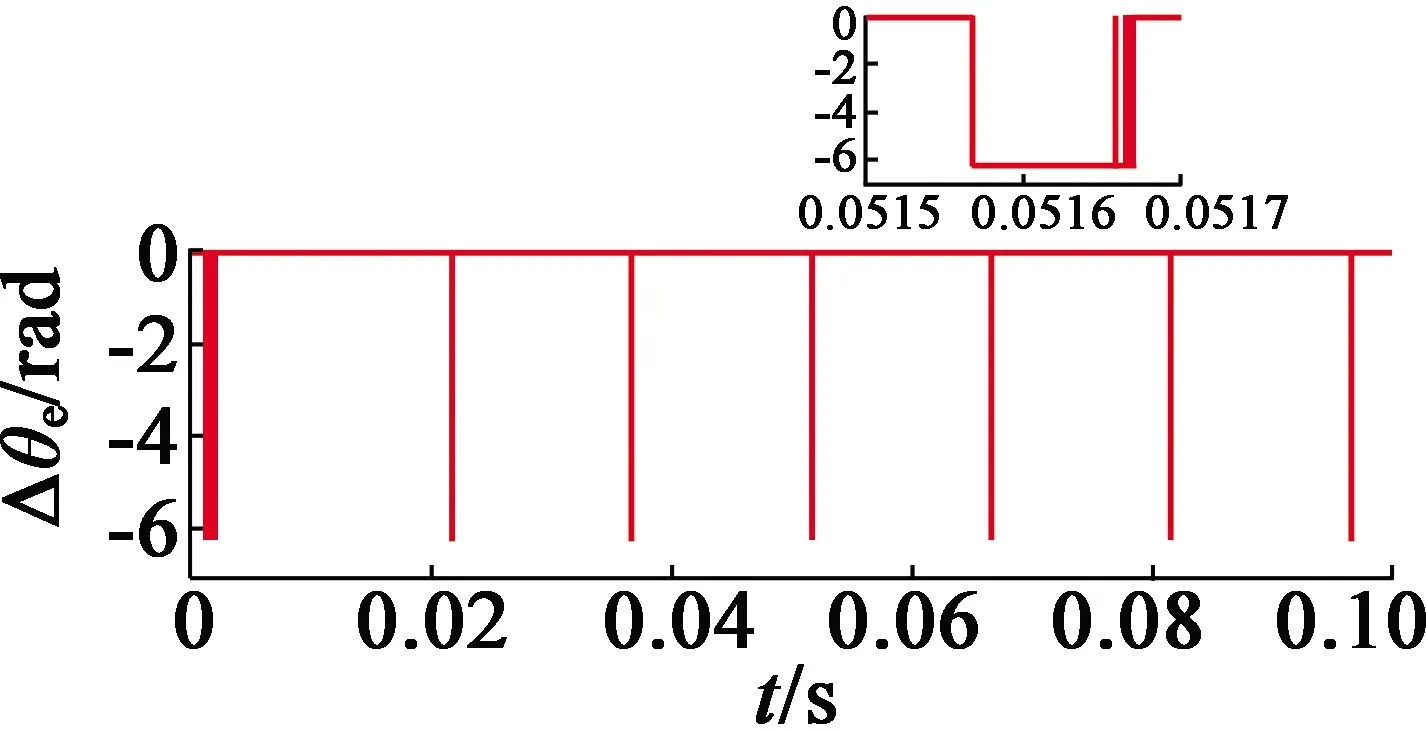
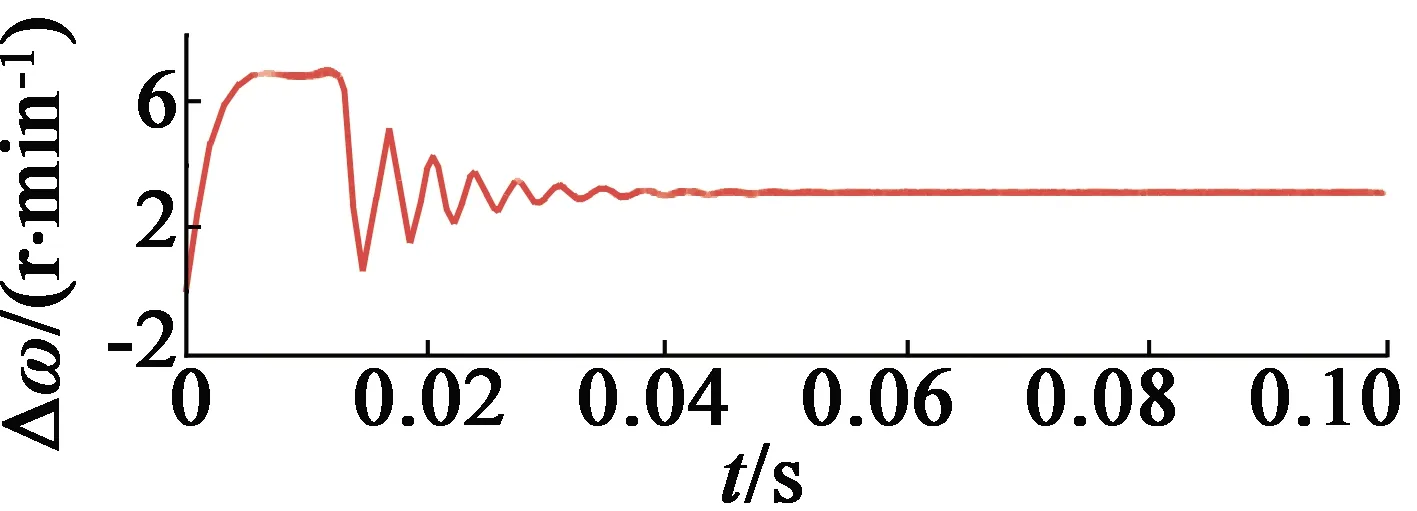
式中:δ>0(0 由式(6)与式(7)建立误差方程: (9) (10) 当|e1|>δ时估计误差可表示: (11) 当|e1|<δ时,估计误差可表示: (12) 因此,在选择参数时,尽可能使|β2|≫wo,β1尽可能小,这样稳态误差e2才能取得较小的值。 在观测出感应电动势后就可以根据以下公式计算转子的转速与位置: (13) 与传统矢量控制系统类似,本文电流环与转速环均采用PI调节器进行调节。控制系统结构如图1所示。 图1 基于ESO的PMSM矢量控制系统 本文在MATLAB /Simulink平台上进行仿真实验,PMSM参数如表1所示。 表1 PMSM主要参数 基于式(7)搭建观测器仿真结构如图2所示。 图2 ESO仿真结构图 无位置传感器控制系统中设置ESO的参数β1=100,β2=6 000 000,a1=0.65,a2=0.5,δ=0.01。相比于文献[13]中线性观测器,本文增益较小,就可以达到控制效果。以下是给定1 000r/min,空载情况下起动电机仿真结果。 感应电动势估算值如图3所示,从图3可以看出,通过非线性ESO的方式可以获得平滑的感应电动势估算值。 图3 感应电动势eα,eβ估算值 图4为电机估计速度与实际速度的对比图。从图4可以看出,非线性状态观测器的转速值已经能较好地跟踪真实值,实现了系统无位置传感器矢量控制,并具获得了较好的控制效果。 图4 ESO的估算速度与真实速度 采用非线性ESO估算的感应电动势精度较高,则转子位置的估计精度也比较高。下面将ESO与常用的sign函数和sat函数构建的两种滑模观测器进行对比,三种观测器均采用双闭环PI调节器。设置电流环、速度环PI参数和电机参数相同。采用sat函数的滑模观测器中设置δ=0.01。 (14) (15) 三种观测器的观测角度与角度误差如图5、图6所示。由图5,图6可以看出,传统的基于sign函数的滑模观测器在起动时,角度的观测会有一个较大的误差。ESO与采用sat函数的滑模观测器角度观测误差相对要小。 (a) 滑模观测器 (b) sat函数-滑模观测器 (c) ESO (a) 滑模观测器 (b) sat函数-滑模观测器 (c) ESO 三种观测器的到的速度误差如图7所示。从图7可以看出,采用sign函数的SMO无位置传感器控制系统,速度的估计会出现较大的波动。采用ESO的无位置传感器控制系统和采用sat函数滑模观测器的无位置传感器控制系统的速度观测值误差相对比较平滑。在起动阶段,基于ESO的无位置传感器控制系统速度估计值误差更小,能更快地跟踪速度变化,说明非线性ESO比两种传统的滑模观测器具有更高的观测精度。 (b) sat函数-滑模观测器 (c) ESO 本文设计了一种ESO对PMSM的转子位置和速度进行观测,通过在MATLAB/Simulink上进行仿真,验证该方法的可行性,并与常用的两种滑模观测器进行了观测效果对比。仿真结果表明:基于ESO进行PMSM位置观测的方案能准确地获取转子转速与位置信息,并且在电机起动阶段与两种传统的滑模观测器相比,ESO具有更高的观测精度,实现了PMSM无传感器矢量控制,为实现PMSM无位置传感器控制中转子位置辨识方法提供思路。

3 仿真分析



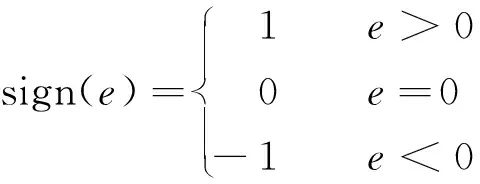






4 结 语
