磁悬浮列车应用场景多普勒分集技术研究
2020-07-09梁建英刘先恺侯圣杰马汉城
梁建英,刘先恺,侯圣杰,田 毅,马汉城
(中车青岛四方机车车辆股份有限公司,山东 青岛 266000)
0 引言
在高速铁路环境中,当列车移动速度大于250 km/h时,多普勒效十分明显[1]。而高速磁悬浮列车最大运行速度为600 km/h,产生的多普勒频偏会严重破坏OFDM子载波之间的正交性,带来载波间干扰,进而降低OFDM系统性能[2-3]。多普勒分集技术将多普勒频偏作为分集增益来源,进而提高OFDM系统在高速移动环境中的性能。高速磁悬浮环境中存在强磁场,且环境复杂多变,很难保证接收机可以获得高信噪比。这样的环境下传统LS信道估计带来的误差会对多普勒分集性能造成不利影响,因此对多普勒分集技术在中低信噪比条件下的信道估计算法进行研究很有必要。
文献[4-5]对单载波系统的多普勒分集技术展开研究。文献[4]设计了基于时-频相关的接收方案来减少多径和多普勒效应对系统性能的影响。文献[5]研究了快时变平坦衰落信道中的多普勒分集技术,将接收信号正负频率偏移部分进行匹配滤波,然后合并,实现多普勒分集。由于OFDM系统自身特点会导致其在高速移动场景中产生严重的载波间干扰,而单载波系统中的多普勒分集技术无法解决此问题。文献[6]针对OFDM系统多普勒分集技术展开研究,对接收信号进行频移产生多种分集支路最终进行加权相加。但文章研究过程中忽略了信道时变性,选择在频域直接对各支路信号进行加权,在时变信道下性能严重下降。文献[7]针对时变信道提出一种新的时-频处理方案来降低误码率,该研究中各支路信号的合并放在了OFDM解调之前即时域上进行,虽然有效降低了信道时变性对研究性能的影响,但在由于信号传输过程中在时域上呈现卷积特性,而频域呈现乘积特性,因此在时域进行加权合并会严重增加算法复杂度。文献[8]提出了简化的多普勒分集技术,利用频域估计出的信道参数计算各支路信号时域权重,在不降低多普勒分集性能的前提下降低了实现复杂度。但该方案中权重是否准确仍然受到频域信道估计准确性的制约。关于信道估计与多普勒分集性能之间的关系,也有学者进行过定量分析。文献[9]研究了高速移动无线通信环境下信道估计误差对多普勒分集性能的影响,通过简单的重复码分析前导符号与数据符号之间的能量差异对分集性能的影响,确定了最优的前导符号与数据符号的能量配比。文献[10]则是将这种研究手段进一步应用到单输入多输出系统中,文章分析了信道估计误差对系统性能的影响,然后利用分析结果对前导符号进行设计,尽可能减小信道估计误差,提高分集增益。文献[11]则是利用MMSE信道估计方案来减小信道估计误差,减小该误差对多普勒分集性能的影响。文献[12]设计了一种针对快速时变衰落信道的迭代信道估计算法,利用该算法将迭代后的前导符号反馈给发射端,以便更加准确地获得信道状态信息,但这无疑给业务的调度又带来新的麻烦。综上所述,时变信道下较低信噪比的多普勒分集技术研究很有必要。
本文主要考虑磁悬浮应用场景列车高速移动与中低信噪比信道的特点,对多普勒分集技术中的LS信道估计方案进行改进,提高信道估计准确度,并将最大比合并与均衡技术结合,提高多普勒分集系统性能,最后通过仿真分析验证了改进方案的性能。
1 系统模型
1.1 信道模型
考虑无主径的多径环境,无线时变信道的冲击响应可以表示为:
(1)
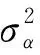
根据OFDM调制原理,一个包含有N个子载波的OFDM符号可以表示为[7]:
(2)
式中,di为第i个调制后的QPSK符号,g(t)表示如下:
(3)
式中,T为一个OFDM符号的持续时间,Tg为循环前缀的持续时间,因此g(t)包含了一个含有循环前缀的完整OFDM符号。
1.2 多普勒分集接收机结构
本文设计的OFDM系统多普勒分集接收机结构如图1所示。接收端首先去掉接收信号OFDM符号中的循环前缀(Cyclic Prefix,CP),然后通过频移处理得到接收信号在多个频域的分集支路,通过FFT变换将各支路信号变换到频域,利用信道估计的结果对每条支路上的对应子载波进行最大比合并(Maximal-Ratio-Combining,MRC)及频域均衡,然后对信号进行解调与信道译码,最终输出信号[13]。
经过时变信道后,在接收端去掉循环前缀的接收信号经过采样后可以表示为:
(4)
式中,Ts为采样时间,为方便分析且不失一般性,将Ts设定为1,则一个OFDM符号的持续时间T可以通过T=N×Ts=N来计算得到。

图1 OFDM系统接收端多普勒分集结构Fig.1 Doppler diversity structure at the receiving end of OFDM system
去掉循环前缀后的信号经过Q-1次频移处理后得到频移分别为fxq的Q个频偏支路,可得到频率偏移为fx的分集支路上第i个子载波的频域信号X(fx,i):
Xs(fx,i)+Xi(fx,i)+N(fx,i),
(5)
式中,Xs(fx,i)为频率偏移为fx的分集支路第i个子载波上的有效信号,Xi(fx,i)表示其他子载波对第i个子载波造成的干扰,N(fx,i)表示噪声。下面对这3个组成部分进行定义。
其中,Xs(fx,i)表示为:
(6)
定义H(fx,i)为频率偏移为fx的分集支路第i个子载波上的信道增益,且与Xs(fx,i)具有关系:Xs(fx,i)=H(fx,i)di,则其表示如下:
(7)
从式(7)可看出,H(fx,i) 由Np个{fDp-fx}构成的复指数分量线性组合而成,在接收端基带处理过程中,该信道增益可由OFDM系统信道估计求得。
式(5)中,Xi(fx,i)表示为:
(8)
式(5)中,N(fx,i)表示为:
(9)
Xi(fx,i)与N(fx,i)均会对后续接收端处理过程造成不利影响,而N(fx,i)由信道决定,与接收端处理流程无关,而Xi(fx,i)由该支路频偏fx决定,因此在选取频偏支路时需要考虑各支路之间的相互干扰。
2 多普勒分集关键模块与参数分析
2.1 信道估计
由以上分析可知在多普勒分集接收过程中要对每个子载波上的多径时变信道增益H(fx,i)进行信道估计。基于前导序列的信道估计方案在复杂度与性能之间较好的平衡,因此被广泛应用。目前主流的基于前导序列的信道估计算法为最小二乘(Least Square,LS)信道估计算法,在高信噪比条件下,该算法可以较好地估计信道增益。但在中低信噪比条件下,LS算法受噪声影响会产生较大偏差,降低多普勒分集性能,而磁悬浮列车应用场景下,接收信噪比很难保证在15 dB以上,因此需对LS信道估计算法进行改进设计。本文将频域信道估计的结果变换至时域,在时域对估计结果进行修正后将其变换回频域,从而有效抑制噪声及信道时变性对信道估计准确性的影响。
OFDM系统帧结构设计如图2所示。在一个或多个OFDM符号前添加一段已知前导序列,实现估计每个子载波上的信道增益,该序列长度与一个OFDM符号的子载波数相同[14]。帧结构中OFDM符号个数根据磁悬浮列车应用场景下信道相干时间确定,每个OFDM符号中循环前缀长度由信道相干带宽确定。对传统的频域LS信道估计算法进行优化,使得系统可在磁悬浮场景下获得更好的性能。

图2 基于前导序列的信道估计方案下OFDM帧结构设计Fig.2 Structure design of OFDM frame in channel estimation scheme based on leading sequence
考虑到列车最大行驶速度为600 km/h,系统工作中心频率为600 MHz,可知信道相干时间约为3 ms,而系统采样率为11.2 MSample/s,因此每个帧最多可采样3 360个采样值。每个OFDM符号包括循环前缀及数据共有294个采样值,因此每个物理帧最多可包含11个OFDM符号,已知的前导序列占其中一个,即每个帧中包含1段已知序列以及10个OFDM符号。而相干带宽的大小取决于信道多径时延,只要循环前缀的长度不小于最大多径时延即可,具体参数见仿真结果。
传统基于前导序列的频域LS信道估计方案中,每个OFDM符号可视为N个并行单载波系统,每个单载波系统同时受到乘性干扰和加性高斯噪声的影响。每个OFDM符号的频域表示式为:
Y(k)=H(k)X(k)+N(k)k=0,1…,N-1,
(10)
式中,H(k)为第k个子载波的信道增益。X(k)在信道估计时可视为前导序列,用于估计每个子载波上的信道增益;在均衡时视为携带未知数据的OFDM符号。N(k)为第k个子载波经过信道时叠加的高斯白噪声,其实部与虚部相互独立,且均服从均值为0的高斯分布。令传统LS信道估计得到的频域信道响应估计值为HLS(k),有:
(11)
利用该方法可估计每个子载波上的信道增益H(fx,i),当信噪比较高时,此算法的性能较为理想,但当信噪比低于15 dB时,传统LS估计产生的偏差会对最大比合并以及均衡的性能造成影响。本文将频域LS信道估计后的信道响应通过IDFT转换于时域,根据阈值将增益较小的点置零,再将时域信道估计结果通过DFT匹配滤波变换至频域,通过时域修正降低高斯噪声带来的影响,且不增加后续最大比合并以及均衡的复杂度。信道估计算法流程如图3所示。

图3 基于时域修正的LS频域信道估计算法流程Fig.3 Algorithm flow of LS frequency - domain channel estimation based on time - domain correction
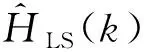
(12)
(13)
式中,Α为判决门限,文中将其设为未修正的每个子载波上的时域信道增益的平均值,其表示为:
(14)
(15)
对每个分集支路上的OFDM符号,分别利用此信道估计算法便可以得到频率偏移为fx的分集支路第i个子载波上的信道增益H(fx,i),进而为最大比合并权值选取以及均衡系数的选取提供参考。
2.2 最大比合并及均衡
传统多普勒分集方案中未考虑均衡过程,仅通过估计出的信道增益补偿各支路信号然后做最大比合并。但在磁悬浮列车应用场景中多普勒扩展导致的载波间(ICI)干扰对OFDM系统影响较大,为减少载波间干扰,本文设计的多普勒分集方案中引入了均衡模块。
最大比合并后第i个子载波上的信号YMRC(i)表示为:
(16)

当接收信号有效信号功率与干扰功率比值(SIR)较大时,干扰项I(i)可以忽略不计,此时可用迫零均衡,则第i个子载波频域均衡系数为:
(17)
式中,
(18)
则经过频域均衡后第i个子载波上的数据为:
(19)
当接收信号SIR较小时,需要考虑干扰项I(i),可采用MMSE方法对接收数据进行均衡,此时第i个子载波频域均衡系数为:
(20)
式中,PI/PS为干扰功率与信号功率的比值,其计算方法见式(21)和式(22)。考虑到循环前缀的引入可以有效减少符号间干扰与载波间干扰,本文采用迫零均衡方法。
2.3 支路频偏参数选取
在确定各支路频偏fx的大小时需要考虑两方面因素:当频偏逐渐增大时,有效信号的功率逐渐减小,而干扰功率逐渐增大,若选取频偏过大,导致有效信号被严重干扰,则会导致接收错误;但当支路频偏过小时,各频偏支路的之间仍然存在较大的相关性,无法获得有效的分集增益。二者均会对多普勒分集的最终结果造成不利影响,因此需要选择合适的支路频偏参数[15]。
由式(6)和式(7)可知,频移为fx的频偏支路第i个子载波上有效信号功率PS(fx,i)可以表示为:
(21)

由式(9)可知,频移为fx的频偏支路上第i个子载波上干扰信号功率PI(fx,i)可以表示为:
(22)

由式(21)和式(22)可以得出SIR与FDT间的曲线图如图4所示,从图中可以看出,当fxT在0~0.5之间时,随着归一化支路频偏fx的增大,有效信号功率逐渐减小,而干扰功率逐渐增加;当fxT取值为0.75或0.8时,SIR随着FDT增大而增大,这说明在多普勒频移逐渐增大时,该频偏支路性能逐渐变好。

图4 SIR与FDT关系曲线图Fig.4 Graph of relation between SIR andFDT
信号间的相关性可以由两路信号间的相关系数衡量,两路信号间有效信号完全相同,因此不相关性取决于两路信号上的干扰信号,因此可以利用信号间干扰信号功率相关系数来衡量两路信号间的相关性。根据相关系数的定义,频偏分别为fx1及fx2的两条支路干扰信号功率相关系数的绝对值为:
(23)
由式(23)可求得当fxT接近0.8时,频偏支路间的相关性最小。图5为不同最大多普勒频偏下,误码率与支路频偏之间的关系,可以看到当fxT处于0.75~0.85之间时误码率性能最佳。
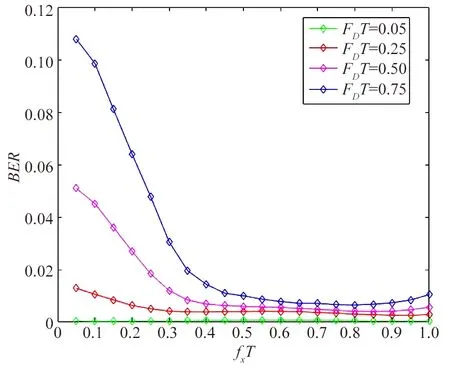
图5 BER与fxT曲线图Fig.5 Graph of BER andfxT
3 仿真结果
仿真参数设置如表1所示。
表1 仿真参数设置
Tab.1 Simulation parameter setting

系统参数取值系统采样率11.2 MSample/s系统带宽10 MHz多径数(Np)6最大多径时延(τmax)32多径时延(τp)均匀分布,(i.i.d),0<τp<τmax多普勒频偏(fDp)均匀分布,(i.i.d),-FD 当信噪比为15 dB时,采用多普勒分集的OFDM系统与无多普勒分集OFDM系统误码率性能如图6所示。当信道中最大归一化多普勒频偏较小时(FDT<0.25),多普勒分集系统的性能并没有明显的改善。但随着FDT的增长,多普勒分集系统的优势逐渐体现出来,相同信道最大归一化多普勒频偏下其误码率明显低于传统OFDM系统。当FDT>0.5时,多普勒分集系统的误码率相比于传统OFDM系统下降一个数量级。这意味着通信双方相对移动速度越快,多普勒分集可以得到越高的分集增益。因此本文设计的多普勒分集技术可以显著提升高速磁悬浮应用场景下OFDM系统的性能。 图6 15 dB信噪比下系统误码性能Fig.6 System error performance under 15 dB SNR 当信道中最大归一化多普勒频偏FD=0.75/T时,采用时域修正LS信道估计算法的多普勒分集系统与采用传统LS信道估计算法的多普勒分集系统误码性能如图7所示,在中低信噪比条件下,采用时域修正信道估计算法的多普勒分集系统误码性能明显要优于采用传统LS信道估计算法的多普勒系统。在信噪比低于16 dB时,本文设计的多普勒分集系统平均可以获得约0.8 dB的增益。 图7 FDT=0.75时误码性能Fig.7 System error performance when FDT=0.75 本文针对磁悬浮场景下高速移动与中低信噪比的环境特点,对传统多普勒分集系统进行优化,针对中低信噪比场景下系统性能受到信道估计准确性制约的问题,对LS信道估计算法进行优化,并将均衡技术加入到多普勒分集接收过程与最大比合并结合起来,使系统达到良好的误码性能。通过仿真证明本文设计的基于OFDM系统的多普勒分集接收技术相比于传统多普勒分集技术在信噪比低于16 dB时高约0.8 dB的分集增益,且相比于传统OFDM系统对于磁悬浮环境有更好的适应性。3.1 多普勒分集对系统接收性能的影响
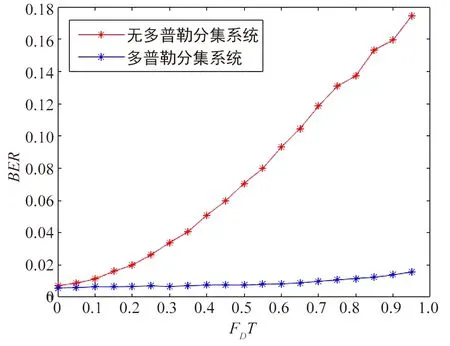
3.2 时域修正信道估计算法对多普勒分集接收性能的影响

4 结束语
