一种基于PEG的构造矩阵在压缩感知中的应用

杜凤强，叶 润，闫 斌

(电子科技大学 传感网络与智能信息处理实验室，四川 成都，611731)

0 引言

随着信息量的不断增加，信号带宽越来越宽，随之而来的采样速率也是越来越高，人们希望降低如此巨大的数据处理压力。在实际应用中，我们获取的信息中大部分是不被利用的，并且这部分的数据对于整体数据并没有太多的影响，那为何不直接去获得我们需要的那部分数据呢？实际上，有损压缩技术在数据处理方面的成果应用从某种意义上验证了人们的设想。作为一种全新信号采样理论，压缩感知打破了传统奈奎斯特理论限制，在信号稀疏或可压缩的基础上，实现数据降维，并通过有效算法，从部分测量数据集中恢复出全局信息。理论一经问世，便取得了广泛关注，近几年在多个领域取得了有效进展。本文基于信道编码理论，对压缩感知测量矩阵进行了浅显的研究，验证压缩感知理论和低密度奇偶校验码间的理论联系，并使用稀疏校验矩阵设计原则构造了压缩感知测量矩阵。

1 压缩感知

压缩感知(Compressed Sensing，CS)是在信号采集的同时完成对信号的压缩，理论本身是“通过对信号的高度不完备线性测量的高精确重建”。假设x(数字图像或数字信号)是n空间中的一个未知向量，其在某个正交基(Wavelet，Fourier等)或紧框架(Curvelet，Gabor等)下有一个稀疏表示：x=Ψθ，其中‖θ‖0≤k，即x为k稀疏信号。对于这样的n维信号x只需m=O(n1/4log5/2(n))个测量样本，即可在特定的算法下准确恢复[1]。

令Φ∈m×n表示压缩感知测量矩阵，令y表示包含m个测量值的实向量。最优的压缩感知过程是通过测量矩阵直接观测出信号x(c∈n)的m个测量值，即求解问题：

CS1:min‖x‖0s.t.Φ·x=y，

(1)

这一问题可看作部分线性解码问题[2]。

在CS1问题求解中，一方面，0范数的求解为NP-Hard问题；另一方面，如果一个问题可以被表示为凸优化(Convex optimization)问题，就可以认定其一定可以得到很好的解决。对于凸优化问题来说，局部最优解就是全局的最优解[3]，可以通过对部分测量信息的求解而得到满足全局信息的解。在满足一定约束的情况下，l0范数求解问题可转化为l1范数下的凸优化问题求解：

CS2:min‖x‖1s.t.Φ·x=y。

(2)

压缩感知理论[4-5]证明了在适当的测量矩阵Φ下最小l0范数优化问题可转化为求解最小l1范数优化问题。在线性稀疏域中，一个“好”测量矩阵Φ∈m×n仅需m=O(klog(n/k))行就可实现k-稀疏信号的高概率重建。

(3)

(4)

此时，对于满足式(4)中零空间特性的测量矩阵，认为问题CS2的求解等价于问题CS1的求解。这一结论在文献[6]中以定理的形式给出。

2 LDPC码与压缩感知的联系

信道编码又称差错控制编码，是一种通过对原始信号添加校验冗余以抵抗错误干扰的技术[7]。在新一代移动通信中，低密度奇偶校验( Low-density Parity-check，LDPC)码[8]作为增强移动宽带场景下数据信道编码方案。线性是指码字信息位与监督位之间为线性关系，二者间满足特定的线性方程组。分组是指在编码过程中将待编码信息进行分组，每组信息码再附加若干监督码。分组码用符号(n,k)表示，n表示码长，k表示码字中信息码元的数目，re=n-k则为监督位数目。分组码的结构为图1所示。

图1 分组码结构Fig.1 Structure of block code

低密度体现在校验矩阵H为稀疏矩阵，即矩阵的行、列中非零元素数目(也称行重、列重)非常小。奇偶校验是奇校验和偶校验的总称，规定了GF(2)中码字中“1”的数目，二者原理相同。以偶校验为例：偶校验中，监督位使得码字中“1”的数目为偶数，即满足：

an-1⊕an-2⊕…⊕a1⊕a0=0，

(5)

接收端若计算为“0”则认为无错码，奇校验同理。

(6)

(7)

为了简化计算及表述简洁，常常将概率比转化为对数形式。又因为平方误差函数是线性的，且一个线性函数总在一个凸集(Convex Set)的极值点中获得最小值，所以对问题CD1的求解又可写作：

CD2:min〈λ,x′〉 s.t.x′∈conv(Ccc)。

(8)

问题CD2的求解复杂度是指数级的，Feldman[9-10]对以上问题的求解进行了转化，对Ccc的凸包(Convex Hull)conv(Ccc)进行了扩展，转而寻找问题的最优解，降低了求解的复杂度。

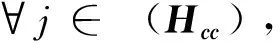
(9)

则Hcc的基础多胞形(Fundamental Polytope)定义为集合：

(10)

(11)

其中

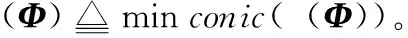
(12)

证明：在矩阵Φ的基锥中，所有的向量ω∈n满足

|ωi|≥0, ∀i∈I(Φ)，

(13)

(14)

令ω≜|v|，显然有任意的ω满足式(13)。当v∈Nullsp(Φ)，对于有即对于有由此，可以得出：

(15)

即任意的向量满足式(14)，得证。

3 G-PEG测量矩阵

为验证稀疏校验矩阵可作为压缩感知测量矩阵，本节基于校验矩阵设计原则构造压缩感知测量矩阵，在现有渐进边生长法基础上提出分组渐进边生成算法(Progressive Edge Growth by Group，G-PEG)，在赋予矩阵一定结构规律的同时，保持了随机特性。矩阵所有校验节点的集合记为C，所有变量节点的集合记为V，实现步骤如下：

步骤3：分组结束条件判断：若Vn的长度为0(n整除m)，结束分组；若Vn的长度小于m(n不能整除m)，将Vn中元素放入最后一个分组slast中，结束分组。

步骤4：确定分组s0连接到校验节点c0。

步骤5：当sj连接ci时，若ci为sj-1的相连节点或者为sj-1相连节点的邻节点，则索引i自增1，当不存在满足条件的i时，sj连接c0。

其中，步骤1对输入参数m和n进行参数计算；步骤2～3对校验矩阵集合进行分组，获得所有变量节点的随机排列；步骤4～5生成边，生成原则为相邻的分组sj所连接的校验节点ci不相同且不相邻。

图2 一维信号重构Fig.2 One-dimensional signal reconstruction

表1 使用不同矩阵测量值重构时间
Tab.1 Reconstruction time using different matrix measurements s

矩阵类型PEG生成矩阵G-PEG生成矩阵运行时间3.987 43.017 7

在一维信号仿真中，由图2可以看出，G-PEG矩阵测量集和PEG矩阵测量集均能够有效地恢复原始信号。以上结果验证了稀疏校验矩阵可以作为压缩感知测量矩阵。表1给出了在不同矩阵测量值下对原始信号重构100次的运行时间。由表1结果可以看出，在相同的条件下，使用G-PEG矩阵作为测量矩阵对于整体运行时间有着明显改善，说明了G-PEG算法能够有效提高矩阵的生成速度。

由图3结果可以看出，在信号稀疏度相同的情况下，使用G-PEG构造矩阵获得的相同测量值具有比其他矩阵更高的重构成功率。这是因为采用G-PEG构造的矩阵，具有比其他测量矩阵更好的不相关性。

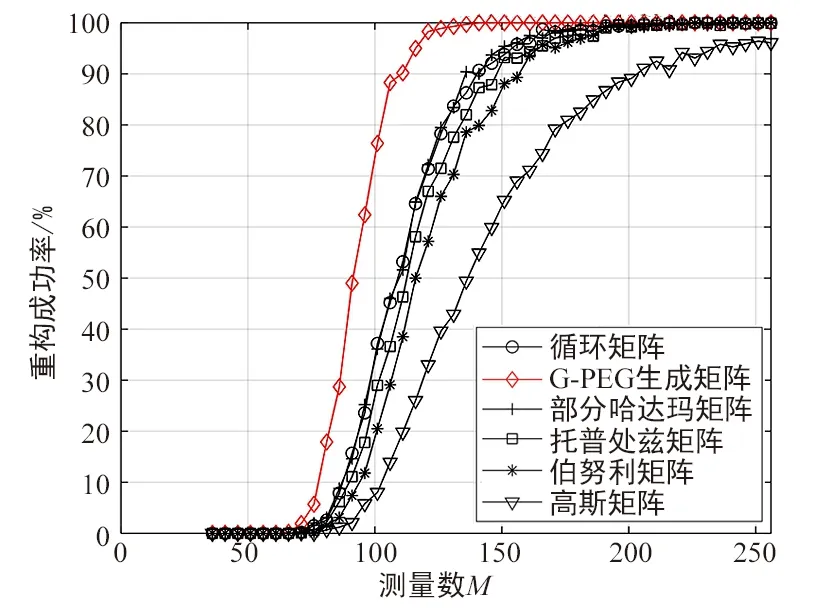
图3 重构成功率与测量数关系曲线图Fig.3 Reconstruction power vs.Measurement number

图4结果显示，在保持测量数M相同的情况下，G-PEG生成矩阵获得的测量集在相同重构算法下具有比其他测量矩阵更高的重构成功率，随着信号稀疏度的增加，优势愈加明显。

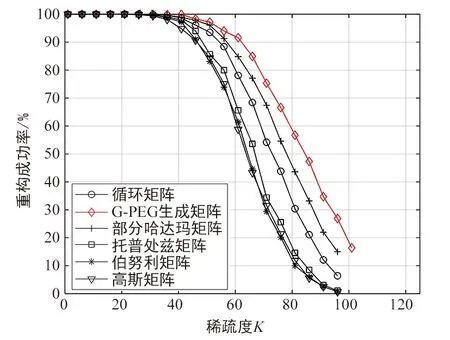
图4 重构成功率与稀疏度关系曲线图Fig.4 Reconstruction power vs.Sparsity

表2展示了G-PEG算法构造的测量矩阵与常用测量矩阵在使用相同重构算法(OMP)时的误差，对比得出：在相同的重构条件下G-PEG生成矩阵能够取得较好的重构效果，对一维信号的重构准确性稍弱于部分哈达玛矩阵，但相较于部分哈达玛矩阵有着更低的复杂度与存储空间，这使得G-PEG算法构造的测量矩阵在整体性能上优于对比的随机测量矩阵。

表2 一维信号重构误差比较
Tab.2 One-dimensional signal reconstruction error

矩阵类型循环矩阵G-PEG生成矩阵部分哈达玛矩阵托普利兹矩阵伯努利矩阵高斯矩阵NMSE0.855 50.876 60.892 90.789 70.764 70.703 4

在二维图像仿真中，采用指纹扫描图像，尺寸为512×512，使用小波(wavelet)稀疏基，重构算法为正交匹配追踪(OMP)。

如图5所示，对于二维图像的重构中，G-PEG生成矩阵优势明显。主要是基于LDPC码构造矩阵其自身的稀疏性，在对于二维图像的采样中，相较于其他测量矩阵获得测量值相关性更强，避免了信息的连续采样。一维信号和二维图像仿真结果表明，基于LDPC码的稀疏测量矩阵不仅能够满足压缩感知的采样需求，并且在二维图像的重构过程中表现出更好的性能。这也验证了G-PEG矩阵是一种性能优良的测量矩阵。

图5 不同测量矩阵重构图像比较Fig.5 Reconstruct image using different measurement matrix

表3 二维信号重构误差比较
Tab.3 Two-dimensional signal reconstruction error

矩阵类型循环矩阵G-PEG生成矩阵部分哈达玛矩阵托普利兹矩阵伯努利矩阵高斯矩阵PSNR20.251 222.761 720.896 319.150 515.428 916.813 7

4 结束语

在压缩感知的实际应用场景中，测量矩阵在信号的采样、压缩、恢复环节扮演着重要角色。G-PEG矩阵在压缩感知中的应用，不仅验证低密度奇偶校验码与压缩感知间的理论联系，同时为测量矩阵的研究提供了新的思路。在压缩感知的应用过程中，研究者应考虑具体场景下的数据特征，构造满足要求的测量矩阵以提高压缩感知的重构效率。