一种变参数模型平方根UKF 锂离子电池SOC 估计方法

高文凯, 严利民,孙 叠

(1.上海大学微电子研究与开发中心,上海200444;2.上海大学机电工程与自动化学院,上海200444)

锂离子电池作为一种能源,广泛应用于便携式设备、电动汽车、可再生能源以及人造卫星等多种领域.与铅酸、镍镉等其他电池比较,锂离子电池具备更高的能量密度、更低的自放电率和较长的循环寿命等品质.然而,锂离子电池过充电或过放电会对电池的性能和寿命造成不可逆的损害.为了保障电池的安全和性能,现代电池管理系统迫切需要一种稳定、精确的荷电状态(state of charge,SOC)估算方法[1].

目前，已有学者提出了多种SOC估计方法[2-9],其中库伦计数法以其算法简单、计算量小等优点而成为应用最广泛的方法.然而库仑计数法是开环估计,累积的电流测量误差可使误差高达25%[4].潘贵财[5]开发了基于模糊逻辑和人工神经网络的智能计算方法用于SOC估计,虽然该方法能够提供准确的估计结果,但是计算成本高,此外还受到训练过程和训练数据集质量的影响.另外,有些文献报道了基于电池状态空间的估计方法,如滑模观测器[6]和扩展卡尔曼滤波(extended Kalman filter,EKF)[7-8].虽然滑模观测器能较好地处理模型的非线性效应,但当输出有噪声时其性能会变差;EKF已被广泛应用于SOC估计,然而EKF中非线性函数(或雅可比矩阵)的线性化近似增大了实现复杂度,同时不准确的雅可比矩阵计算会导致滤波器发散,影响其稳定性.

考虑到以上这些方法存在的问题,本工作结合变参数2阶戴维南等效模型的平方根无迹卡尔曼滤波算法(square root unscented Kalman filter,SRUKF),提出了新的SOC估算方法.SRUKF不需要对非线性模型进行线性化,并且比EKF(1阶)具有更高的误差阶(2阶).另外,SRUKF不需要像常规的无迹卡尔曼滤波(unscented Kalman filter,UKF)那样对状态协方差进行重构.变参数2阶戴维南等效模型能够反映锂电池各项参数随SOC变化的情况,能够比常规的固定参数模型更好地描述锂电池实际工作状态,使SOC的估计值更接近真实情况.该方法经实验验证,与EKF,UKF以及使用固定参数模型的估计值进行了对比.结果表明,本工作提出的基于变参数模型的SRUKF比其他方法具有更低的误差.

1 锂离子电池模型

图1为本工作所提出的锂离子电池变参数2阶戴维南等效模型.在该电路中,可变电阻R0表示为在电池充电/放电过程中的瞬时电压降;采用2组可变电阻-电容(resistorcapacitance,RC)网络来模拟电池充电/放电过程中的驰豫效应.一般来说,这种网络比具有单个RC网络的电池模型具有更高的建模精度,Rs和Cs网络分支模拟电池的短时瞬态响应,而Rl和Cl是用来代表长期的瞬态响应[10].模型中的R0,Rs,Cs,Rl和Cl都是随电池SOC变化的参数.VOC代表电池的开路电压(opening circuit voltage,OCV),Vt为电池端电压,IB为充放电电流.

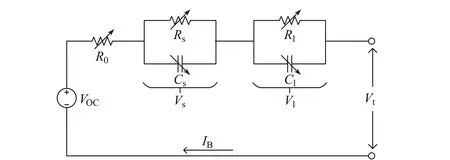
图1 锂离子电池的变参数2阶戴维南等效模型Fig.1 Variable-parameter second-order Thevenin equivalent model for Li-ion batteries

1.1 开路电压与荷电状态的关系

电池的OCV与SOC具有非线性关系.为了获得这一非线性函数,试验使用36 A·h 3.6 V的镍钴锰酸锂(Li(NiCoMn)O2)电池进行复合脉冲功率特性测试(hybrid pulse power characterization test,HPPC).HPPC可以获得在不同SOC水平下相应的OCV,同时也可以对不同SOC水平下相应的电池参数进行计算[11].HPPC的步骤如下:①以恒流-恒压方式将电池充满;②以1 C的电流放去10%的电量(1C为在1 h的时间内将电池电量从0充到 100%的电流,在数值上等于以A·h为单位的电池容量,本实验中为36 A);③静置1 h,此时可测量SOC水平下相应的VOC;④依次进行10 s放电脉冲、40 s静置、10 s充电脉冲,之后重复步骤②∼④9次,分别在SOC为1.0,0.9,···,0.1共10个点上进行电流脉冲试验.图2为HPPC全过程电流脉冲和电压响应曲线.图3显示了从实验中得到的每个SOC水平下相应的OCV曲线.

为了描述图3中OCV与SOC之间的关系,采用多项式曲线拟合

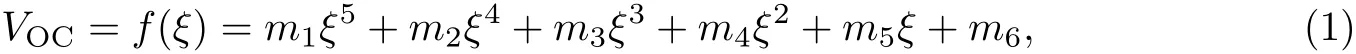
式中:ξ表示为SOC.基于图3中的实验数据,利用Matlab软件中的拟合工具计算出的系数分别为m1=8.388,m2=−28.65,m3=35.58,m4=−19.14,m5=4.743,m6=3.231.此处拟合为一个5阶方程是适当的,产生误差的范数仅为0.019 5.

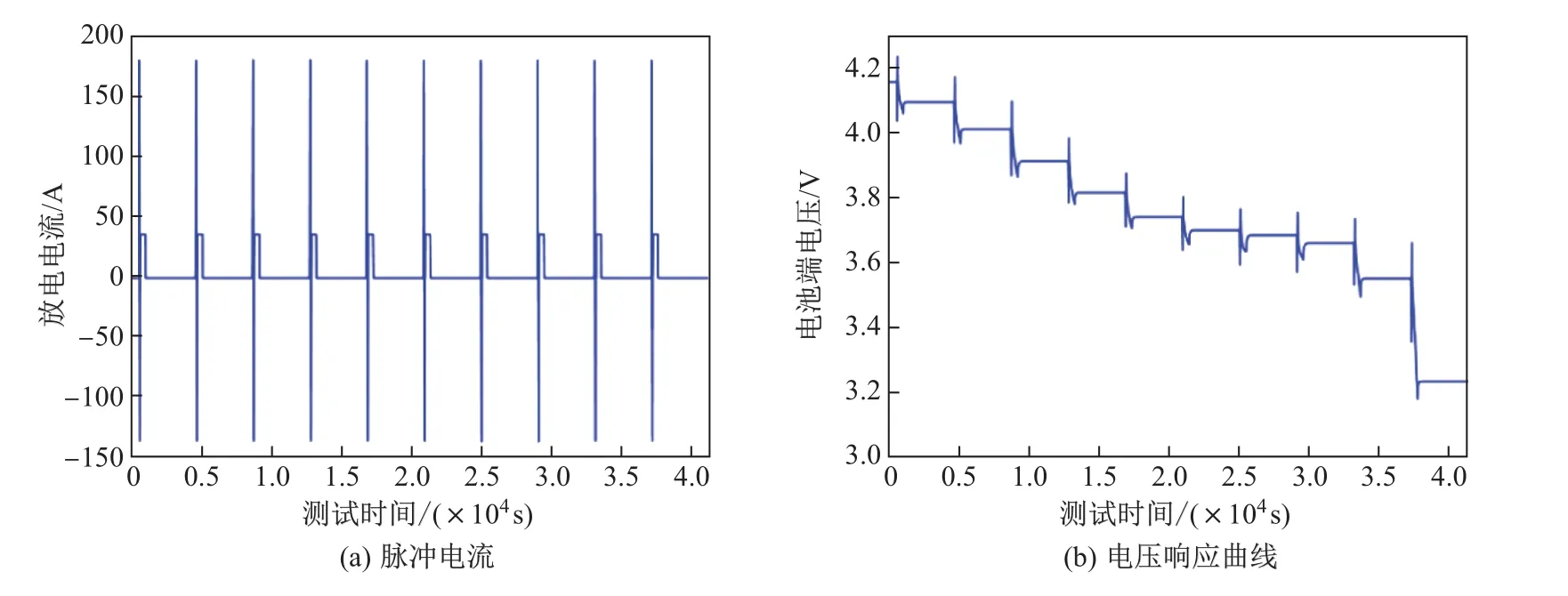
图2 HPPC全过程电流脉冲和电压响应曲线Fig.2 Current pulse and voltage response curves of HPPC

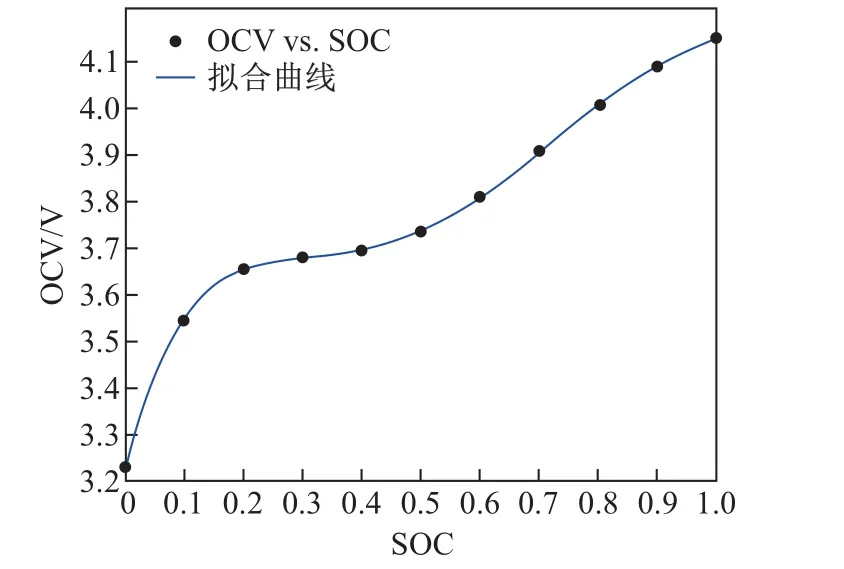
图3 实验得到的SOC-OCV关系及其拟合曲线Fig.3 SOC-OCV relation obtained from experiment and its fitting curve

1.2 电池状态空间方程

电池SOC可以表示为离散时间变量

式中:Qb表示为电池放电容量;IB为放电电流;∆t为采样时间;η为库伦效率.根据基尔霍夫电路定律,2个RC网络的电路动力学方程为

将[ξVsVl]T作为状态变量,由式(2)∼(4)可以得到电池状态空间方程为

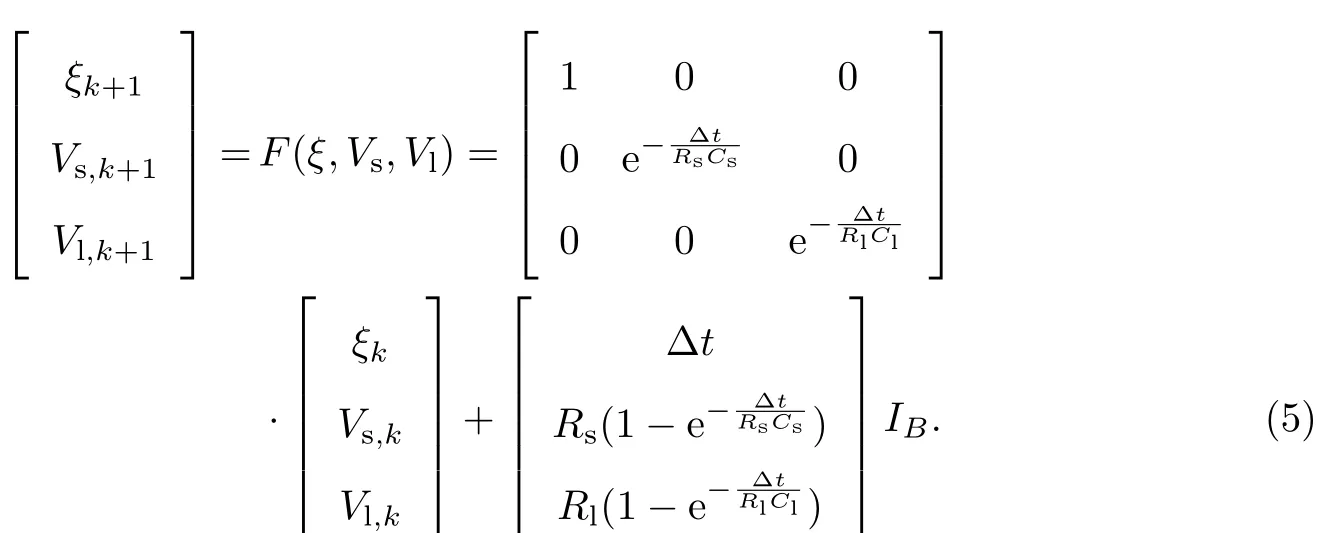
根据图1,以电池端电压Vt作为系统输出,以充放电电流IB作为系统输入,可以获得Vt的测量函数H为

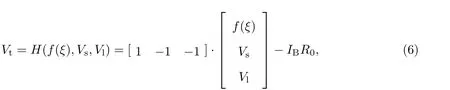
这里,为了估计ξ,Vs和Vl,需要知道电池参数R0,Rs,Rl,Cs和Cl.

1.3 电池参数的提取

在本工作中,使用传递函数法来识别所需的电池参数[12].在频域的电池端电压可以写成

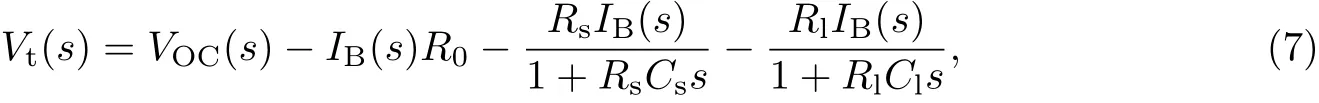
式中:S为拉普拉斯变换变量.考虑Vt−VOC作为输出,电流IB作为输入,则能够导出传递函数G(s)为

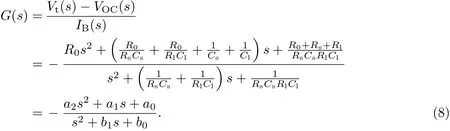
通过在HPPC中不同的SOC间隔内注入充放电脉冲,并测量相应的电压响应,可以识别出传递函数和辨识参数.图4为在90%的SOC下充放电脉冲和电压响应的一个示例.

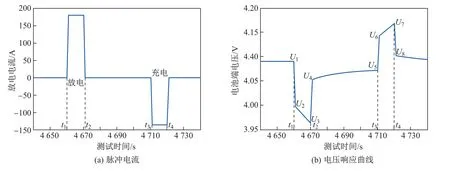
图4 HPPC单个电流脉冲和对应的电压响应曲线Fig.4 Single current pulse and corresponding voltage response curve in HPPC

利用注入的电流脉冲和相应的电压响应,可以得到传递函数G(s)的系数(a2,a1,a0,b1和b0).通过求解这些系数,能够得到电池参数(R0,Rs,Cs,Rl和Cl).在每个SOC水平上,针对每个测量电压识别不同的传递函数并辨识参数.由于参数的变化对SOC有重要的影响[9],故不能取参数的平均值,而要使模型中的这些参数随SOC的变化而变化,这就是变参数模型.表1列出了已辨识的电池参数,图5为利用所得到的SOC-OCV关系和电池参数在Matlab软件上建立的锂电池变参数2阶戴维南等效模型.

为了验证所建立的电池模型,在模型上进行同样的HPPC.真实电池的电压响应和模型的电压响应及其绝对误差分别如图6和7所示.从图7中能够看出,在施加充放电脉冲时,端电压最大绝对误差小于50 mV,说明利用所得到的SOC-OCV关系和电池参数建立的电池模型能够准确地表示出真实电池的工作状态.

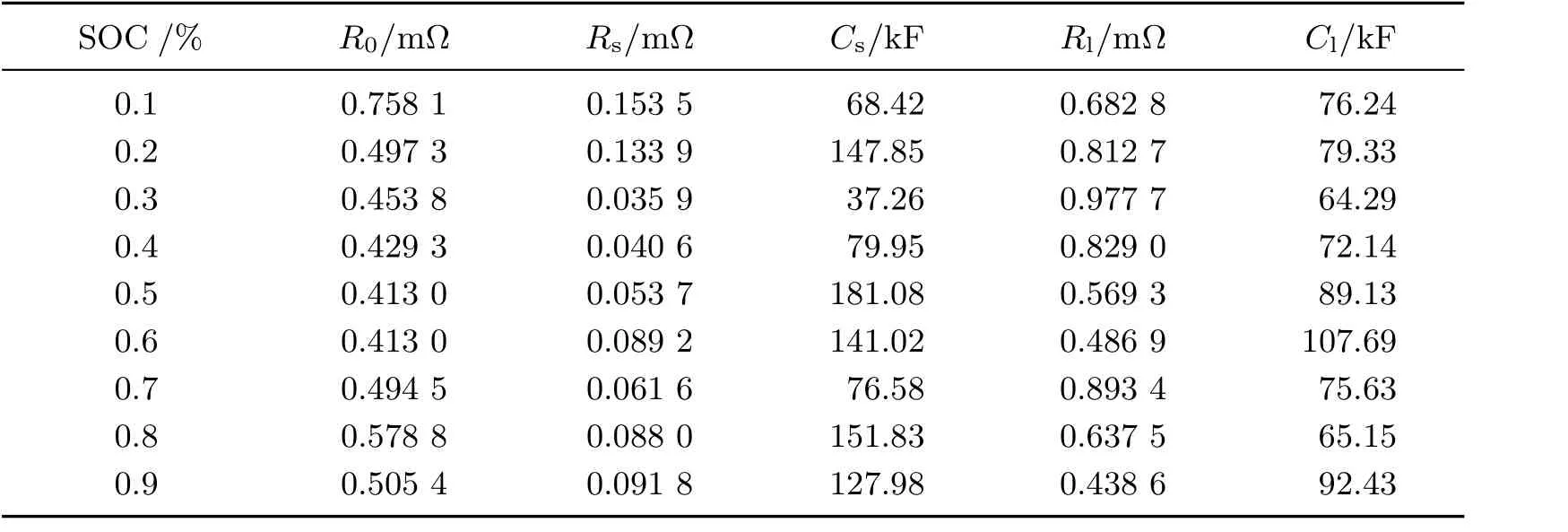
表1 参数识别结果Table 1 Results of parameter identification

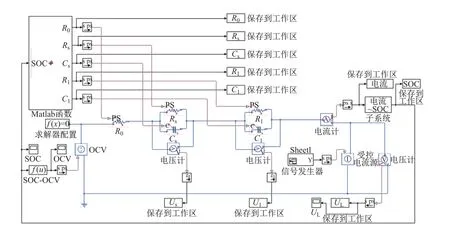
图5 在Matlab软件上建立的变参数2阶戴维南等效模型Fig.5 Variable-parameter second-order Thevenin equivalent model based on Matlab software

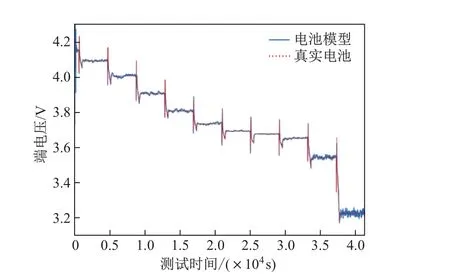
图6 真实电池电压和模型电压的比较Fig.6 Comparison between real battery voltage and model voltage

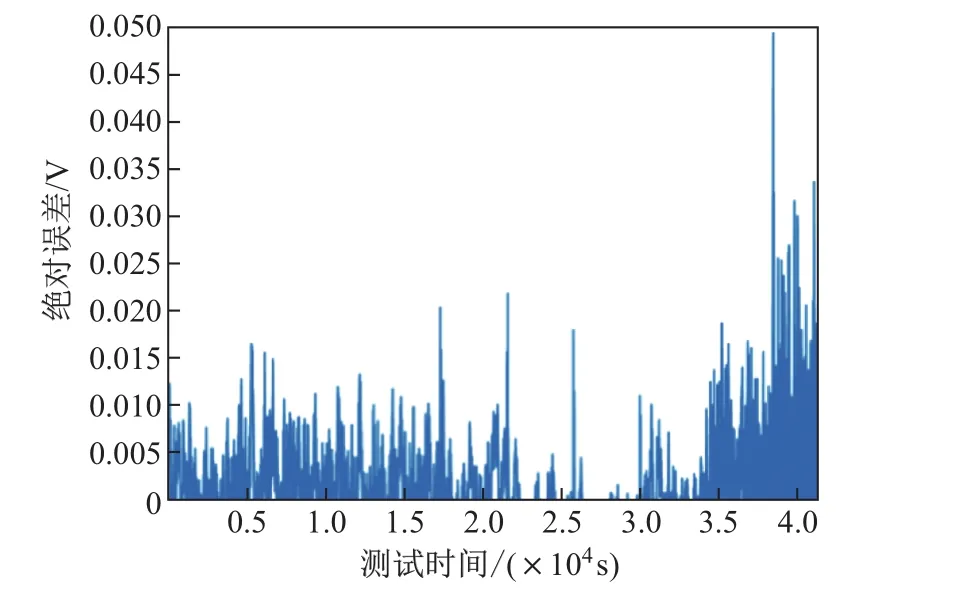
图7 模型电压的绝对误差Fig.7 Absolute errors of model voltage

2 平方根无迹卡尔曼滤波SOC估计算法

本工作引入了SRUKF算法,运用矩阵的QR分解和Cholesky分解来处理UKF算法在数字计算的稳定性和状态协方差的半正定性方面存在的问题[13].

卡尔曼滤波的主要思想是,结合前一时刻状态的估算量、新的系统输入量和观测量,通过系统的状态转移方程得到当前时间的状态估计.通常非线性系统离散状态空间方程为

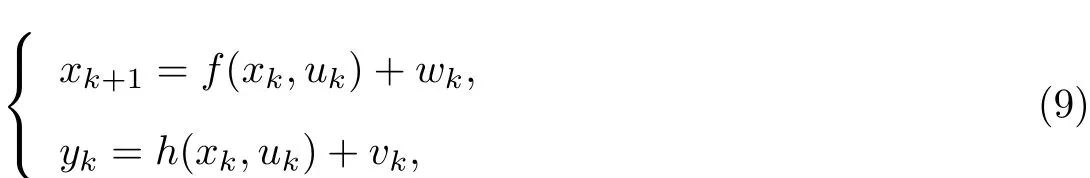
式中:x为状态变量[ξ VsVl]T;y为观测变量Vt;f为非线性状态转移方程(见式(5));h为非线性观测方程(见式(6));wk,vk为状态变量x与观测变量y的高斯白噪声,其方差矩阵分别为

当估算系统的状态时,需要预先给出状态量的初始值.设状态量的初始值为bx0,初始状态估算误差的协方差P0的Cholesky分解因子为S0,则有

2.1 无迹变换

每一时刻状态变量的均值bx与协方差P的Cholesky分解因子S,经过无迹变换获得2n+1个(n为状态变量的维数)采样点(称为Sigma点集)与其权值ω,Sigma点集的选择通常根据先验均值和先验协方差矩阵平方根的相关列来实现:

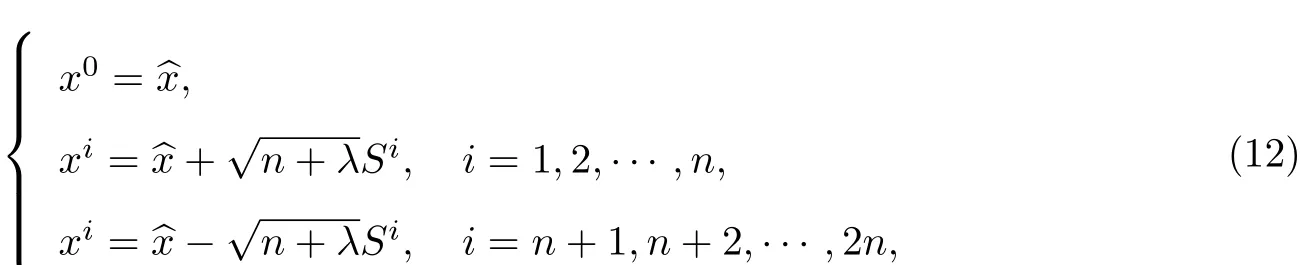
式中:Si表示为S的第i列.Sigma点集权值的计算为

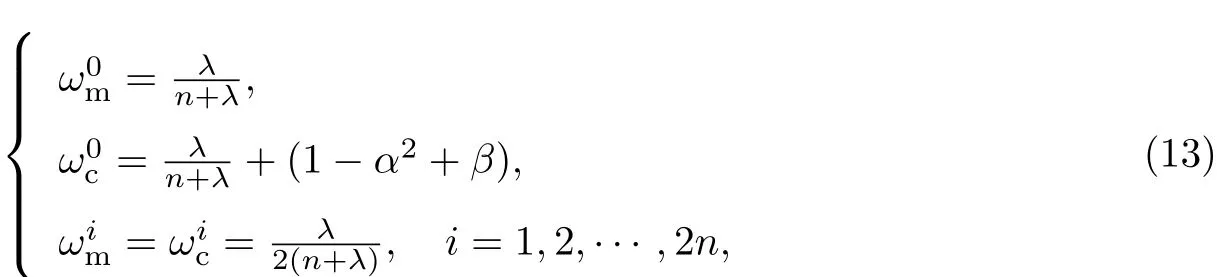
式中:ωm为Sigma点集均值的权重;ωc为协方差的权重;参数λ=α2(n+ki)−n是一个缩放比例,能够降低系统总的估计误差;α与采样点的状态分布有关,通常将α设为较小的正值以降低高阶矩的影响;β是一个非负权系数,可以减小状态估计的峰值误差,改善协方差的准确度.

2.2 平方根无迹卡尔曼滤波

SRUKF算法的基本步骤如下:

(1)利用式(12),(13)中无迹变换得到2n+1个采样点及其对应的权值,即

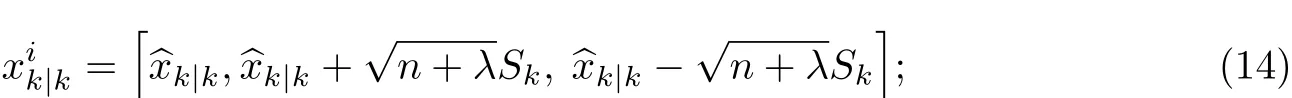
(2)通过系统的状态转移方程,计算这些采样点的一步预测,

(3)由Sigma点集的一步预测和Sigma点集的权值ω计算状态量的一步预测均值,

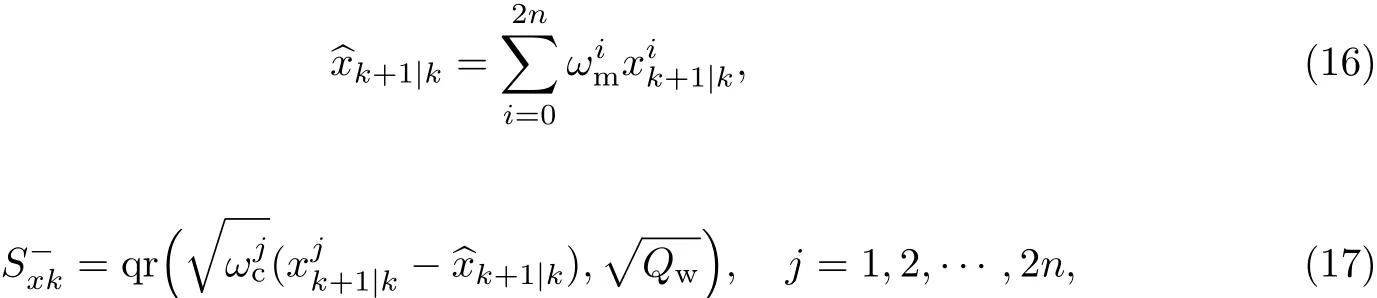
(4)由Sigma点集的一步预测值和系统输入量,通过系统的观测方程,计算得到系统观测量的2n+1个预测值,

(5)2n+1个观测量预测值加权求和,获得系统观测变量的预测均值以及观测变量协方差的Cholesky因子,

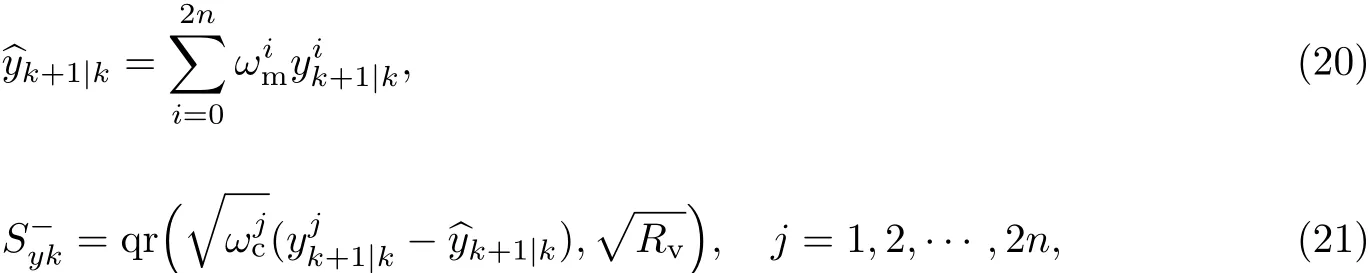
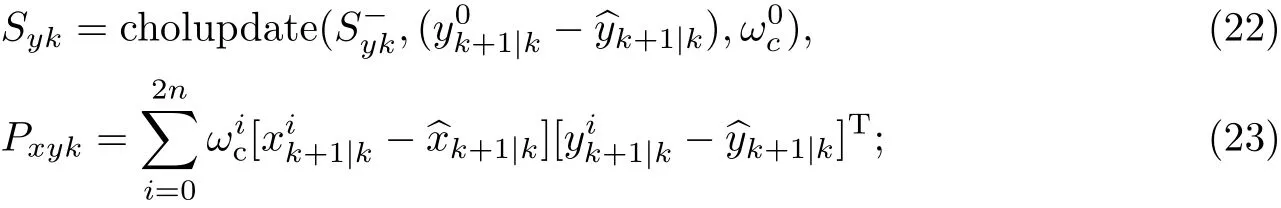
(6)计算卡尔曼增益矩阵,

(7)利用K更新,

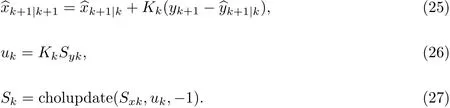
3 实验结果与讨论

为了验证所提出的方法,将上述对36 A·h 3.6 V的Li(NiCoMn)O2电池做HPPC时获得的电池充放电电流数据,与端电压数据分别输入给应用在变参数模型的EKF,UKF和SRUKF算法,将这3种方法得到的SOC估计值与HPPC过程中记录到的电池SOC真实值作对比,其结果如图8所示.图9显示了3种估计算法所得结果的绝对误差,可以发现在初始的一段很短的时间内3种方法误差均较大,原因是对于算法来说初始SOC值是未知的,因此需要一定的时间将估计值收敛到真实值.从图9中还可以看出,3种方法均能在200 s内收敛到真实的SOC,收敛时间非常短,说明这3种卡尔曼滤波算法都有着较好的收敛性.在3种算法的结果都收敛到真实SOC时,可以直观地看出SRUKF的误差是相对最小的.为了准确评价这3种不同的SOC估计方法的性能,分别计算其估计结果的最大绝对误差、平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE),结果如表2所示.在3种同样应用于变参数模型的SOC估计算法中,SRUKF的3项指标都是最小的,这表明SRUKF对SOC的估计有着更高的精确度.

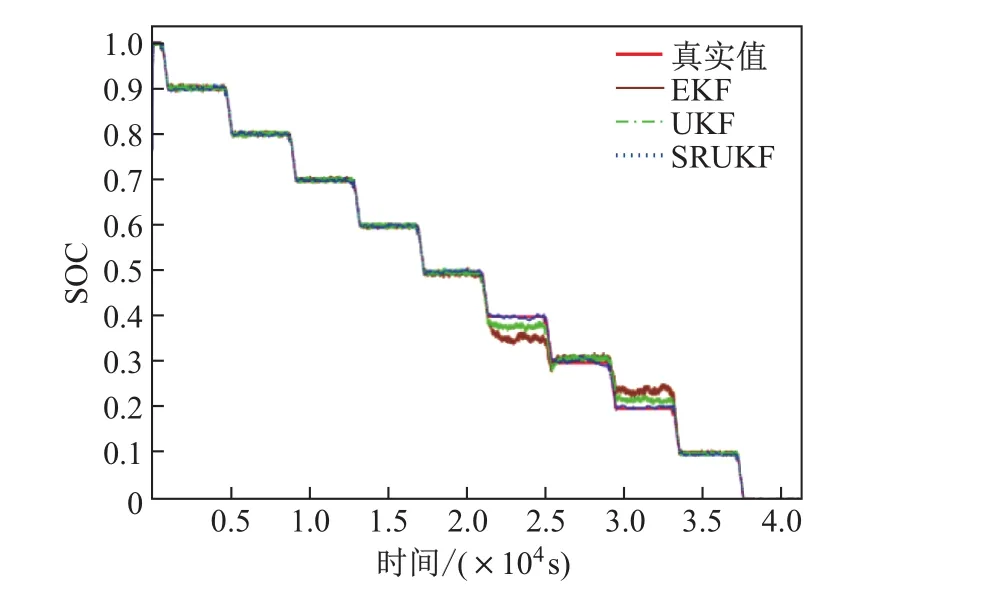
图8 3种SOC估计算法结果对比Fig.8 Comparison between results of three SOC estimation algorithms

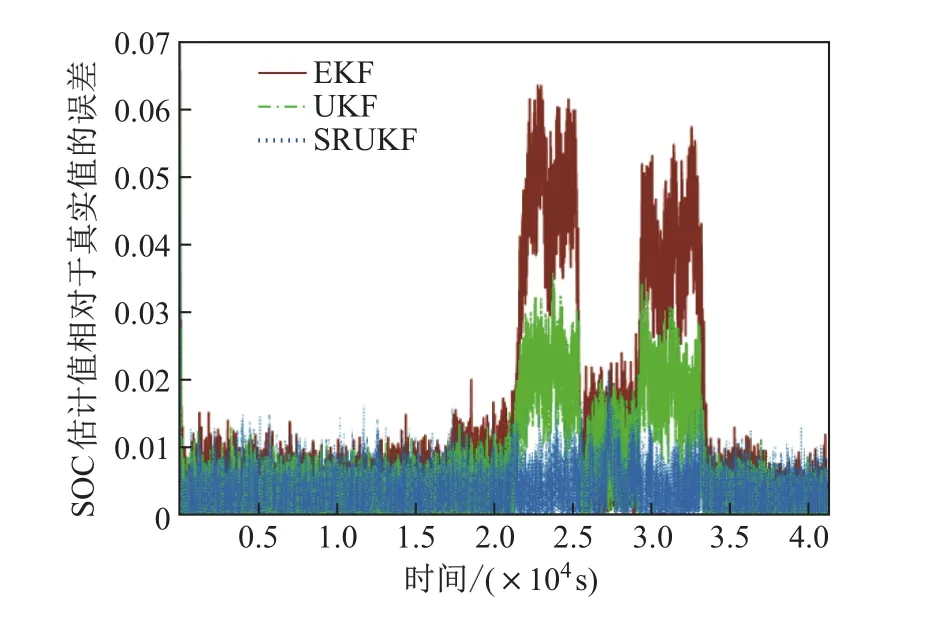
图9 3种估计算法的绝对误差Fig.9 Absolute errors of three estimation algorithms

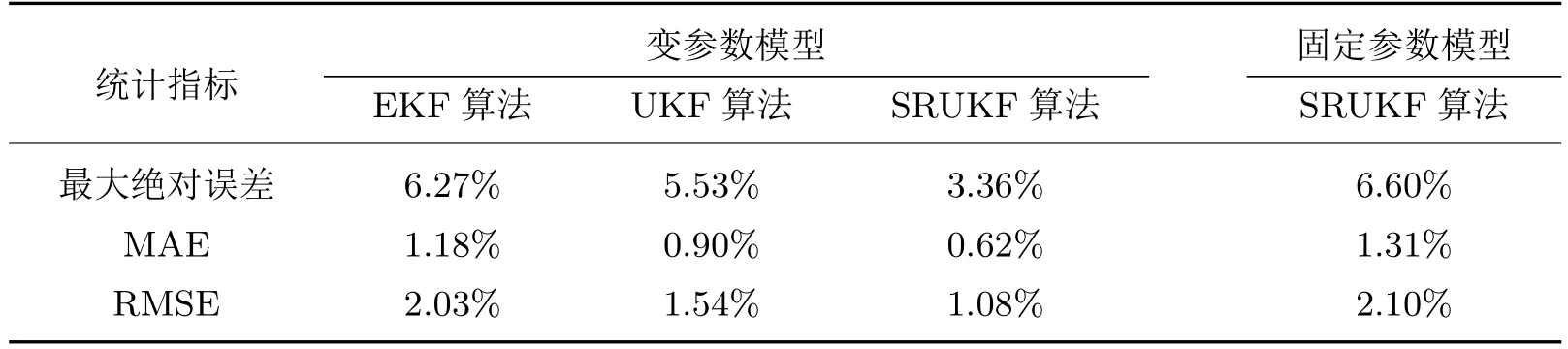
表2 各估计算法的误差指标Table 2 Error indexes of each estimation algorithm

为了将本工作所建立的变参数模型与固定参数模型作对比,将辨识出的不同SOC水平下的各项参数取平均值作为这些参数的固定值,建立常规的2阶戴维南等效模型;并在此模型上应用SRUKF,输入同样的电池充放电电流数据与端电压数据,将所得的SOC估计结果与变参数模型下得到的估计结果作对比,结果如图10所示.图11显示了2种模型所得结果的绝对误差,可以直观地看出变参数模型的误差是相对较小的.为了准确评价2种模型的SOC估计方法的性能,分别计算其估计结果的最大绝对误差MAE和RMSE,其结果亦列于表2中.从表2可以看出变参数模型的3项指标比较小,说明应用于变参数模型的SOC估计算法有着更高的准确度.

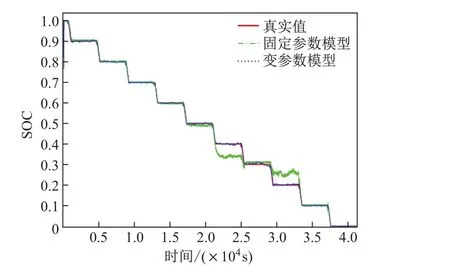
图10 SRUKF分别应用在变参数模型和固定参数模型上的估计结果Fig.10 Estimation results of SRUKF applied to the variable-parameter model and the fixedparameter model respectively

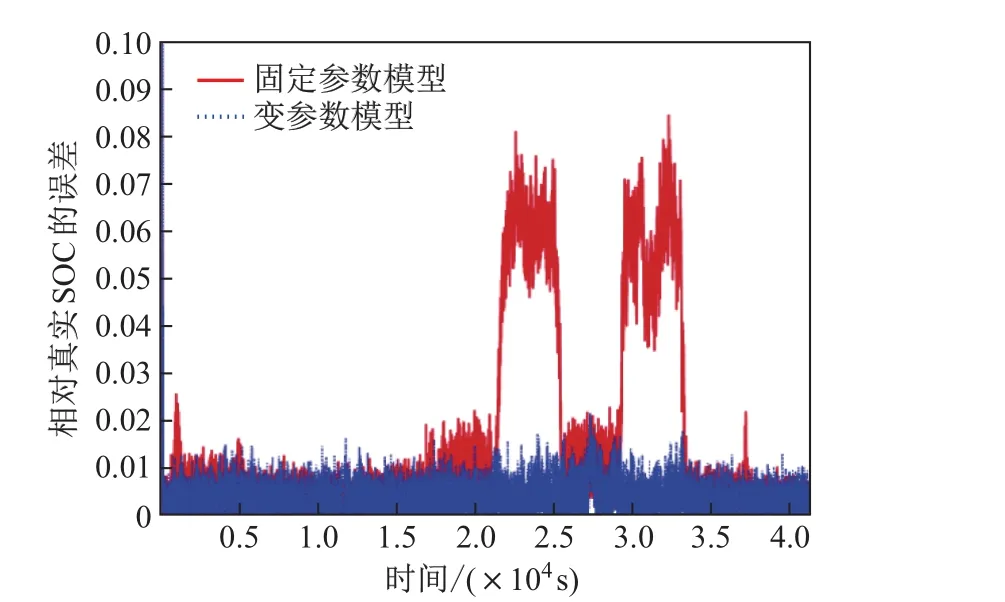
图11 固定参数模型与变参数模型的绝对误差Fig.11 Absolute errors of fixed-parameter model and variable-parameter model

为了进一步验证本工作所提出的SRUKF与锂电池变参数模型结合的方法在SOC估算方面的准确性,本工作与其他文献中同类使用SRUKF估算SOC的结果进行了比较.其中文献[14]使用了SRUKF估算SOC,该文献亦考虑了电池模型参数随SOC变化的状况,但没有应用如本工作类似的变参数模型;文献[15]则采用了做球面变换的SRUKF来估算SOC,该方法对SRUKF算法本身进行了改进,降低了计算要求,对比结果如表3所示.从表3中可以看出,采用本工作的方法估算SOC的准确性比其他2种文献中的方法高.

表3 本方法与其他文献中同类方法的比较Table 3 Comparison between the method in this paper and the similar methods in other literatures

4 结束语

本工作为改善锂离子电池SOC估算的准确性,在锂离子电池2阶戴维南等效模型的基础上,建立变参数模型以提高电池模型的精确度,并在此模型上应用SRUKF算法进行锂离子电池的SOC实时估计.该算法不存在EKF中线性化处理非线性函数时产生的误差,同时解决了UKF中难以分解非正定矩阵的问题,优化了数字计算的稳定性和状态协方差的半正定性.经过实验结果的分析,证实了在变参数模型上应用SRUKF的方法估算电池SOC具有较强的实用性、较快的收敛性和较高的准确性.