基于SA-PSO的多平台多型反舰导弹组合攻击目标分配模型研究∗

（海军航空大学岸防兵学院 烟台 264001）

1 引言

反舰导弹携带平台众多，有空基、海基、潜艇、岸基四种平台。随着战争信息化程度加快，现在战争更加趋近于体系作战，以单型号反舰导弹进行攻击的传统攻击模式已经很难适应现代化海上战争，多平台多型反舰导弹武器协同作战才能获得更加理想的对敌毁伤效果。多平台多型反舰导弹协同作战是未来战争的主体作战方式，在进行体系作战中，合理分配反舰导弹，部署我方反舰导弹对敌方目标进行打击，是提高导弹毁伤效能的重要手段［1～2］。

2 目标问题分析

多平台多型反舰导弹组合攻击目标分配问题是一个约束众多的优化问题，按照一定的约束条件与优化原则将要打击的目标分配给不同的火力单元，以期待达到最佳的毁伤效果，属于火力分配范畴［3］。在目标火力分配领域，目前已经有较多的研究成果，例如文献［4］研究了导弹对目标打击火力分配问题，引入了毁伤下届作为约束条件来优化目标函数；文献［5］研究了基于先期毁伤准则的防空火力分配问题等。

在多平台协同作战中，以信息技术为纽带，将实时的态势感知、准确的情报分析、精确地火力打击连为一体，形成一体化的整体作战能力。为了更加充分地发挥反舰导弹体系的作战效能，需要对体系中不同平台的反舰导弹单元进行必要的打击目标分配［6～7］。

3 目标分配模型

3.1 基本作战想定

假设该问题为红蓝对抗问题，红方为多平台协同作战，蓝方由m艘舰艇组成的舰艇编队。红方为多平台协同作战，具有n种不同类型的反舰导弹，每型导弹的数量为NMi(i=1,2,…,n)，共有N枚弹。假设反舰导弹具备航路规划能力，红方发射的导弹都可以到达蓝方舰艇，并以一定的概率对蓝方舰艇进行毁伤，作战目标毁伤程度区间如表1所示。

表1 作战目标毁伤程度区间

3.2 约束条件

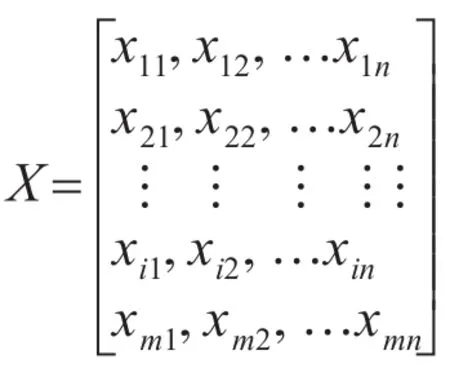
其中，表示非负整数。

2）毁伤要求约束，对目标舰队毁伤下届规定β,β∈[0 , 1]，即目标函数F(x)≥β。设定毁伤下界的目的在于保证对目标毁伤的可靠性。

3.3 舰艇编队综合价值Vj

舰艇编队综合价值是编队中单个舰艇总体价值Sj。与单个舰艇威胁程度wj按照一定比例加权求和获得，ω1、ω2为权重系数。舰艇的总体价值需要综合考虑舰艇的经济价值、政治价值、军事价值等因素；舰艇的威胁程度需要综合考虑舰艇的战斗能力指标与舰艇类型指标。根据作战任务情况，与舰艇各自的实际情况赋予舰艇不同的权重系数值，经过加权来确定舰艇编队整体的综合价值。即

其中0＜ω1,ω2＜1，且ω1+ω2=1。

引入舰艇编队综合价值的目的在于更好的完成作战任务，直击要害，更符合作战目的。

3.4 多目标分配目标函数

多平台反舰导弹体系组合攻击时的目标分配比单一的反舰导弹单元攻击时的目标分配要复杂得多。设F(x) 为目标毁伤效益函数。下面通过分析目标函数里的变量和因素值对最大毁伤的目标函数进行建模。

1）导弹综合毁伤概率

第i反舰导弹的单枚毁伤概率pij为

2）第j艘舰艇的毁伤概率Pj

设为第i型反舰导弹对敌编队第j艘舰艇的毁伤概率，则

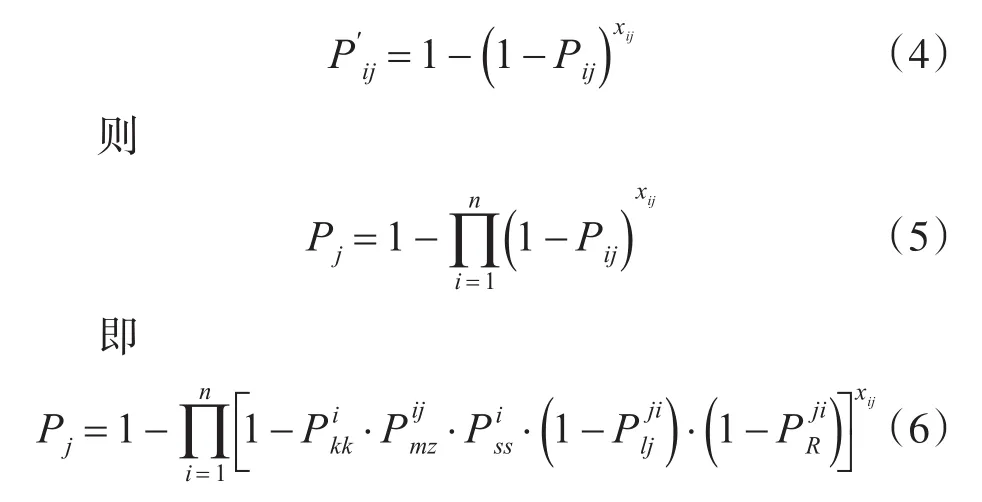
编队所有舰艇毁伤概率之和为

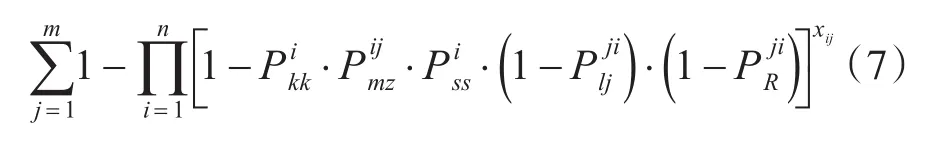
则舰艇编队毁伤效益模型为

则最大毁伤模型为

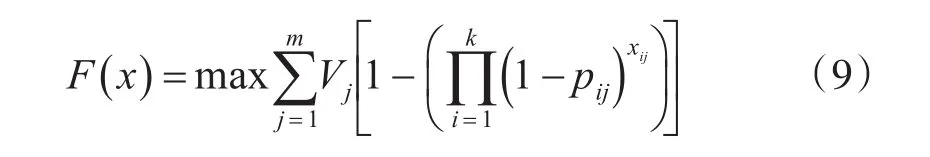
综上所述，最大毁伤效益模型为

4 模拟退火的粒子群算法

4.1 基本思想

模拟退火算法（Simulated Annealing，SA）来源于固体退火原理，是一种基于概率的算法，最早是由Metropolis提出。将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小［8～9］。

粒子群算法（Particle Swarm Optimization，PSO）是一种源于对鸟群捕食行为的研究而发明的进化计算技术，它通过不断迭代来搜寻目标函数的最优值，开始算法初始化一组随机解，而每个粒子都可看成是问题的潜在解［10～12］。为了克服标准粒子群搜索算法在函数优化中出现的迭代速度慢、精度低且易陷入局部最优等缺点，将两种算法进行融合。粒子群算法可以控制寻优方向，模拟退火算法在搜索过程中具有一定概率的突跳能力，在接受新解时既可以接受好的解也能以一定的概率接受坏解，可以解决局部收敛问题。该混合算法不仅提高了算法的灵活性与多样性，还能提高粒子的多样性，充分发挥了粒子群算法的快速收敛性和模拟退火的全局搜索能力。在解决反舰导弹体系攻击目标分配问题时，具有极高的效率，从而使得混合算法获得了较强的全局与局部优化能力。

4.2 算法步骤

1）初始化微粒的速度和位置；

2）计算种群中每个微粒的目标函数值；

3）更新个体最优位置和群体最优位置；

4）对微粒个体最优位置进行SA搜索；

5）更新各微粒的个体最优位置；

6）选择最优，更新群体最优位置；

7）群体最优位置是否满足？是，输出；否，转步骤4）。算法总体流程图如图1所示。

图1 总体算法流程图

4.3 算法公式

基于模拟退火的微粒群算法采用带压缩银子的PSO优化算法，速度和位置公式如下：

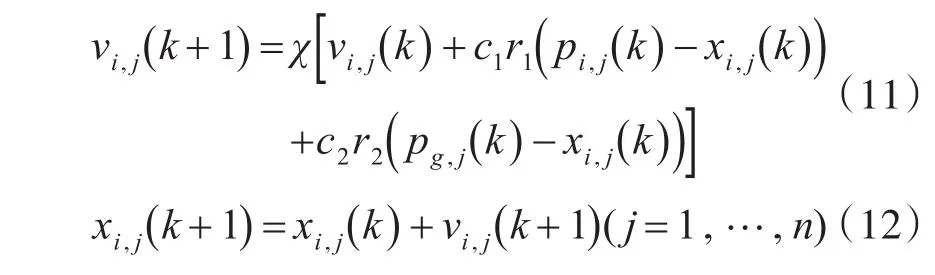
其中，压缩因子：

借用SA算法公式，即突跳概率公式为

其中f为目标函数值进行计算。

5 实例验证

红方为多平台协同作战，由两艘驱逐舰，两架飞机，一艘潜艇和岸舰导弹部队组成；蓝方由一艘驱逐舰和两艘护卫舰组成的舰艇编队。红方具备4种不同平台类型的反舰导弹，其中两艘驱逐舰携带某型反舰导弹的数量为16枚，飞机携带某类型反舰导弹的数量为6枚，潜艇携带某类型反舰导弹的数量为4枚，岸舰导弹部队携带某型反舰导弹的数量为6枚。其中，通过专家评判法对目标舰艇进行价值评判，目标舰艇的总体价值为S=(0.4,0.3,0.3)，权重为0.6；目标的威胁程度为W=(0.25,0.4,0.35) ，权重为0.4。最后得到舰艇综合价值为V1=0.34;V2=0.34;V3=0.32。四种类型的反舰导弹对目标的综合毁伤概率见表2。

用SA-PSO算法进行寻优，按照上述约束条件为（10），设c1=1,c2=2 。

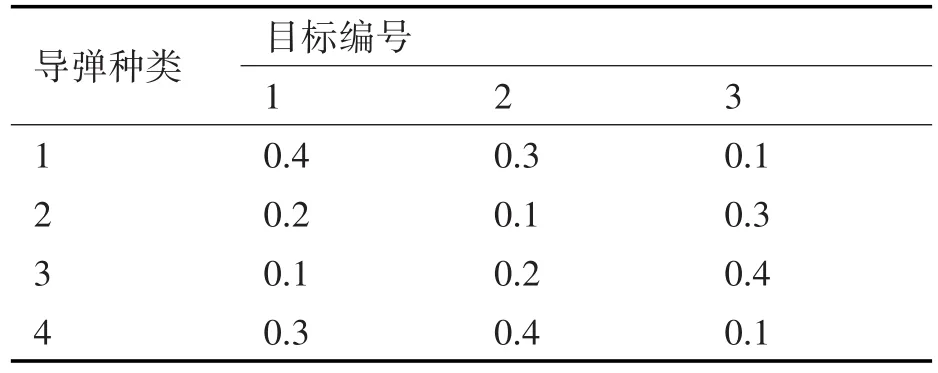
表2 4类导弹对目标综合毁伤概率

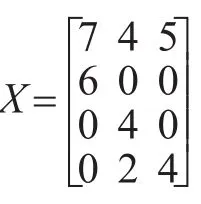
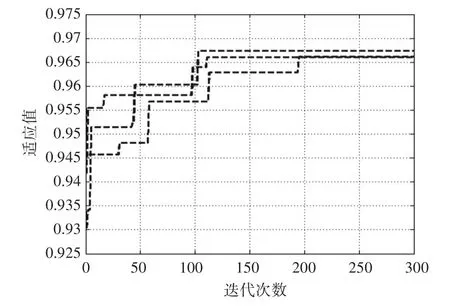
图2 最大毁伤值曲线图

如图2所示，在种群设为300时，对目标函数进行多次运行后，分别运行到110代和200代左右就得到最优目标函数值。计算结果收敛的速度越来越快，收敛的结果越来越好，得到的最优函数值为0.9674，可以达到压制性毁灭的结果。结果可以为指挥员提供一定的参考。

6 结语

本文从多平台多型反舰导弹作战想定出发，综合考虑多种因素，建立了多平台多型反舰导弹打击目标的火力分配模型，利用改进了位置和速度公式的SA-PSO算法对最大毁伤模型进行了求解。具有操作方法简单，通用性强等特点，实例计算结果也表明模型有一定的参考价值，算法收敛性好，稳定性高，通过全局寻优可以较快得到火力分配方案，该模型和算法结果可供决策者参考。