运用坐标系变换 简化宏程序编程

摘 要：本文论述在我们机械加工过程中，无论是数控车床，还是数控加工中心，有时会遇到加工非圆曲线零件，诸如椭圆、抛物线、双曲线、正弦、余弦函数图形，或者有规律布置的几何图形，这时就会涉及到宏程序编程，而非圆曲线的数学方程变化比较繁琐。本文提出通过编程坐标系变换，可以简化数学方程式，从而达到简化宏程序编程的目的。

关键词：非圆曲线;坐标系变换;宏程序;数控加工

1. 前言

在我们机械加工过程中，无论是数控车床，还是数控加工中心，有时会遇到加工非圆曲线零件，诸如椭圆、抛物线、双曲线、正弦、余弦函数图形，或者有规律布置的几何图形，这时我们就会涉及到宏程序编程。宏是一段具有一定独立功能的汇编代码。而数控宏程序就是用变量代替常量来表述一个地址数字值的程序。

数控宏程序由于在程序中使用了变量、算术和逻辑运算及条件转移，使得编制相同加工操作的程序更方便，更容易。宏程序其具有以下基本特点：

1.1高效性

在数控加工中，常遇到数量少、品种繁多、有规则的几何形状的工件，在编程中只要把这些共同点进行分析与总结，把这些几何形状的共同点设为变量应用到程序中，只需改变其中几个变量中的赋值，就可通过多次调用进行加工。这样大大节省了编程时间，而且在运用中准确性也大大提高。

1.2经济性

在加工中经常出现品种多数量少的零件，这些零件在某些特征上变化不定，如果采用常规的加工方法，需要定制许多类型的成形刀具，制作这些刀具既费时又加大制造成本，而采用宏编程就可以降低制造成本。

1.3多功能性

宏程序的功能包含多个方面：

（1）、同一类相同特征不同尺寸的零件，给定不同的参数，使用同一个宏程序就可以加工，编程得到大幅度的简化。

（2）、非圆曲线的拟合处理加工

对于椭圆、双曲线、抛物线等可以用数学公式描述的非圆曲线的加工，数控系统一般没有这样的插补功能，但是应用宏程序功能，可以将这样的非圆曲线用非常微小的直线段或圆弧段拟合加工，得到满足精度要求的非圆曲线。

（3）、曲线交点的计算功能

对于一些复杂零件的交点、切点坐标，不用人工计算，只要输入已知的条件，节点坐标可以由宏程序计算完成，在很大程度上增强了数控系统的计算功能，降低了编程的难度。

所以，宏程序的功能非常强大，宏程序是程序编制的高级阶段，是数控机床编程功能的提高和扩展。因此，宏程序的编制要求编程人员有多方面的基础知识：

1.4数学基础知识

编制宏程序必须有良好的数学基础，数学知识的作用有多方面：非圆曲线如椭圆、抛物线、双曲线的直角坐标系方程和参数方程的转换;不同位置的函数方程的转换;在加工规律曲线、曲面时，必须熟悉其数学公式并根据公式编制相应的宏程序拟合加工。

1.5计算机编程基础知识

宏程序是一类特殊的、实用性极强的专用计算机控制程序，其中许多基本概念、编程规则都是从通用计算机语言编程中移植过来的。所以，学习计算机语言，有助于快速理解并掌握宏程序。

2. 问题的提出

在我们的实际生产数控加工中一般遇到加工的非圆曲线图形只是单个的诸如椭圆、抛物线、双曲线。且坐标系建立在这些图形的中心上。对于这样的工件图形，其数学方程比较简单。例如椭圆直角坐标方程X2/a2+Z2/b2=1，参数方程X=a*sinα  Z=b*cosα;抛物线标准方程X2=2*P*Z;双曲线标准方程X2/a2-Z2/b2=1   参数方程X=a*secα    Z=b*tanα。如果在数控编程的图形上出现这样简单的数学模型，且几何图形的中心在数控编程坐标系的原点上，那么在编制宏程序时，只要在车床的对刀过程中将刀具补偿参数设置在非圆几何图形的中心上，这样函数方程的变化比较简单，也好理解。椭圆直角坐标方程的变化形式X=a*SQRT（1- Z2/b2）， 抛物线标准方程的变化形式X=SQRT（2*P*Z）， 双曲线标准方程的变化形式X=a*SQRT（1+Z2/b2）。

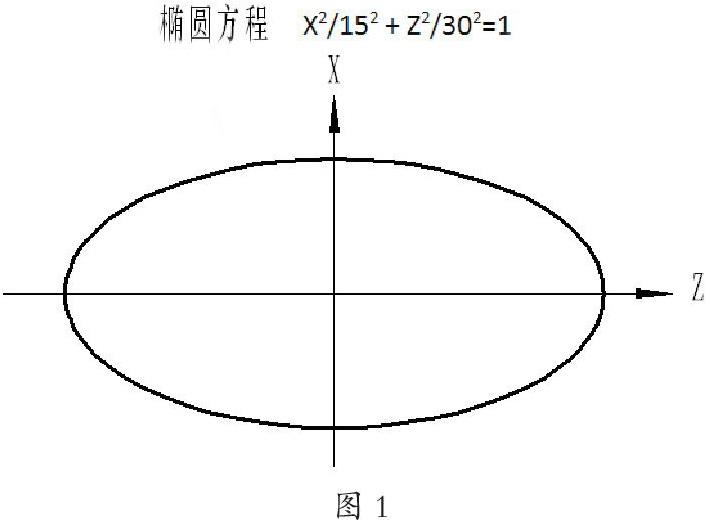
例如：对如下图所示的椭圆，长半軸是30，短半轴是15

由于，其中心在坐标系的原点上，所以该椭圆方程为X2/152 + Z2/302=1。方程式比较简单，好理解。

但是，如果在数控编程的图形上出现这样的非圆曲线图：非圆曲线的中心不在数控编程坐标系的原点上，而是在X轴和Z轴的方向上都偏移原点一段距离，并且是有2个或者以上的非圆曲线图形，那么这些非圆曲线的方程式就开始变得比较复杂，麻烦了。这样对于数学基础较薄弱的人来说变得比较困难，且不好理解。

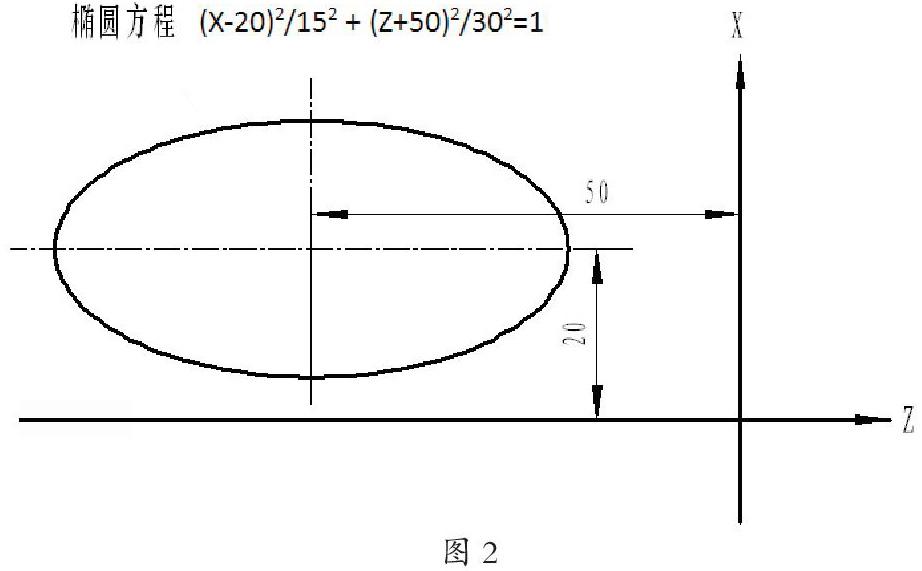
例如：如下图所示的椭圆。同样是：长半轴是30，短半轴是15。

由于该椭圆的中心不在坐标系的原点上，而是在X轴和Z轴两个方向上发生了偏移，这样，方程式就变得复杂了。在方程式X2/152 + Z2/302=1的基础上进行了数学变化，新位置的椭圆方程变为（X-20）2/152 + （Z+50）2/302=1。

对于双曲线、抛物线、正弦曲线等非圆曲线图形，它们的数学处理方式和上面的椭圆方程是一样的。

3. 解决的方法

对此，为了简化非圆曲线数学方程式的内容，我们可以在数控机床的 MDI面板上输入刀具补偿的过程中通过坐标系偏移即分别建立几个坐标系G54，G55，G56。把每个非圆曲线的中心相对于基准坐标零点在X、Z方向的偏移计算出来，然后分别输入到各自的坐标系中：G54，G55，G56。这样，对于非圆曲线有坐标系偏移的情况，我们在书写方程式的时候，不必理会其图形偏移以后的数学方程式是什么样，而只要按照非圆曲线的中心在坐标系原点的方程式格式书写出图形的函数方程即可。

例如：在数控编程图中如果出现图2那样的带坐标系偏移的图形，我们先把该曲线中心相对于坐标系原点的偏移量计算出来，X轴偏移20，Z轴偏移-50。注意：由于是采用直角坐标系编程，X20需要变成X40。这样，我们就把X40，Z-50输入到G55坐标系中。然后，对于椭圆方程式，我们不用写出（X-20）2/152 + （Z+50）2/302=1这样的方程式，而只要写出X2/152 + Z2/302=1这样的方程式即可，再對它进行数学变化。

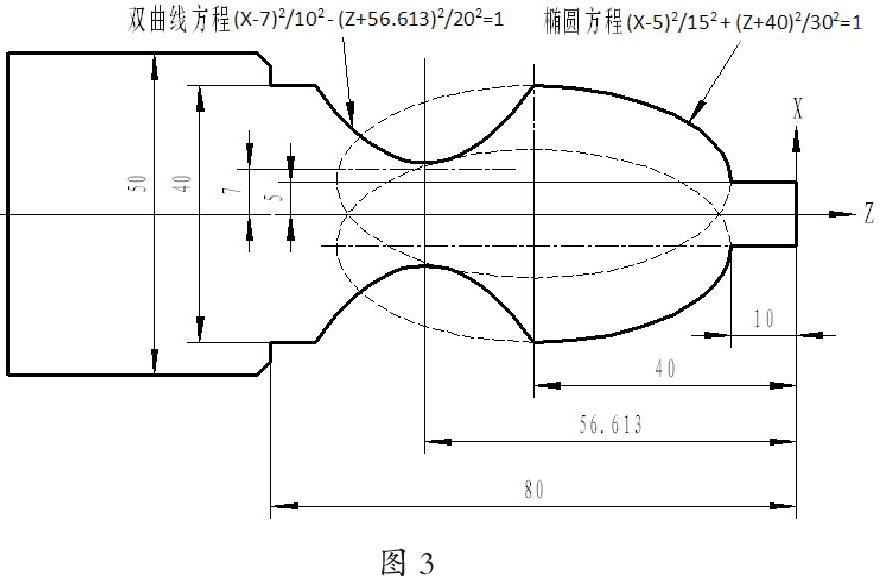
现在，我们以下图为例，详细说明一下坐标系偏移的刀补输入过程以及在坐标系偏移的情况下如何编制宏程序。

如图3所示，我们可以看到，有2个非圆曲线：椭圆和双曲线相连接，并且这两个非圆曲线在X轴和Z轴两个方向都发生了偏移。在以右端面建立的坐标系中，椭圆方程为（X-5）2/152 + （Z+40）2/302=1，双曲线方程为（X-7）2/102 - （Z+56.613）2/202=1。另外，图中的尺寸基准为工件右端面。这样，我们以右端面为基准坐标系，可以建立3个坐标系：3个坐标系分别为右端面是G54坐标系，椭圆的中心是G55坐标系，双曲线的中心是G56坐标系。通过计算，椭圆中心相对于基准坐标系偏移值为X5，Z-40。双曲线中心相对于基准坐标系偏移值为X7，Z-56.613。

由于采用直径编程，把椭圆中心的偏移值X10，Z-40输入到数控系统G55坐标系上。如下图所示：

把双曲线中心的偏移值X14，Z-56.613输入到数控系统G56坐标系上。如下图所示：

这样就完成了非圆曲线坐标系偏移的参数设置。然后，采用试切法对工件进行对刀。试切工件的端面后在G53坐标系上输入Z0，再点击软键【测量】;试切外圆，输入X直径值，再点击软键【测量】，对刀完成。G53基准坐标系建立完毕。如下图所示：

这样，在以后的宏程序编制过程中，椭圆方程只按照方程式X2/152 + Z2/302=1，双曲线方程只按照方程式X2/102 - Z2/202=1进行数学变化就可以了。

下面是根据图3，利用坐标系偏移编制的完整宏程序。

O0001

M03 S800 T0101

G98 M08

G54

G00 X52. Z3.

G90 X45. Z-80. F100

G90 X41.

G55

G00 X42. Z43.

#1=15.

#2=30.

#3=15.

WHILE[#3GE0]DO1

#4=#2*SQRT[1-#3*#3/[#1*#1]]

G90X[2*#3+0.6]Z[#4+0.4]F100

#3=#3-1.

END1

G00 X0.4 Z42.

#5=30. WHILE[#5GE0]DO1

#6=2*#1*SQRT[1-#5*#5/[#2*#2]]

G01X[#6+0.4]Z[#5+0.3]

#5=#5-0.1

END1

G01X31.

G56

#7=10.

#8=20.

#9=8.6

WHILE[#9GE0.6]DO1

#10=16.613

#11=-16.613

WHILE[#10GE#11]DO2

#12=2*#7*SQRT[1+#10*#10/[#8*#8]]

G01X[#12+#9]Z#10F80

#10=#10-0.1

END2

G00 X28. Z16.613

#9=#9-2.

END1

G00 X28.

G54

G00 Z3.

G00 X10.

G55

#5=30.

WHILE[#5GE0]DO1

#6=2*#1*SQRT[1-#5*#5/[#2*#2]]

G01X[#6]Z[#5]

#5=#5-0.1

END1 G56

#10=16.613

#11=-16.613

WHILE[#10GE#11]DO1

#12=2*#7*SQRT[1+#10*#10/[#8*#8]]

G01X#12Z#10

#10=#10-0.1

END1

G54

G01 Z-80.

G01 X46.

G01 X50. Z-82.

G01 X52.

G00 X100. Z100.

M30

结论

对于非圆曲线的复杂数学变换模型，利用坐标系偏置原理，在每个非圆曲线的中心上建立自己的坐标系，再通过数控系统的MDI面板，把每个非圆曲线的中心相对于基准坐标系的偏置量输入到参数坐标系中。这样，就可以实现简化非圆曲线的数学方程式内容，从而达到简化宏程序编程的目的。

作者简介：

仲伟进（1969-），男，山东泰安，大学本科，工程师，高级技师，2013年，在泰安市技能人才职业技能大赛中，获得加工中心组一等奖。2012年，在第四届全国技工院校技能大赛山东省选拔赛数控组中，2016年，在第44届世界技能大赛山东省选拔赛数控车组中，担任评委和裁判。

（泰山科技学院，山东 泰安 271000）