数学期望在农业生产中的应用

张艳玲

数学期望在农业生产中的应用

张艳玲

（衡水学院河北衡水053000）

现代化农业的发展离不开其他领域先进理论和技术的支撑，文章对数学期望与现代农业的结合进行了分析，探讨了数学期望在农业生产中的应用案例，以期可以在农业生产中起到指导作用。

现代化农业；数学期望；应用

“锄禾日当午，汗滴禾下雨”，这首广为流传的古诗道出了劳动人民的辛苦。农业生产受自然环境、气候因素影响外，还受供求关系影响，跟农民自身的文化素质也有很大关系。随着科技的发展和社会的进步，农民逐渐从“看天吃饭，解决温饱”一步步转变为以知识和科技为依托的现代化农业。现代化农民掌握现代化技术和设备，根据气象资料，市场供需情况等，进行分析，组织更高效的农业生产。文章就数学期望在农业生产中的应用做些探讨。

1 数学期望

数学期望是概率论与数理统计中的一个概念。“数学期望”这一词源于一场著名的中途中止的赌局的赌金分配问题，由法国数学家帕斯卡最早提出。数学期望是随机变量取值的平均值，完全由随机变量的概率分布所确定。

若随机变量为离散型随机变量，则数学期望为随机变量取值与对应概率的乘积的和。即

设是离散型随机变量，它的分布率是：

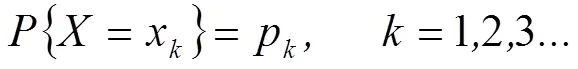
则随机变量的数学期望为

若随机变量为连续型随机变量，则数学期望为随机变量取值与对应概率的乘积的和。即

则随机变量的数学期望为

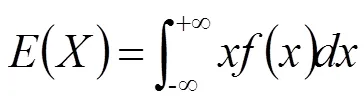
2 数学期望与现代农业的结合

农业生产会受到多种因素的影响，如环境、气候等。现代农业生产不再仅仅是为了解决自家温饱，更需要充分利用现代化的机械、科技，结合现代化的理论知识，将生产作物的经济收益最大化。科学技术蓬勃发展，各个学科也不再单独孤立。数学是其他学科的基础，数学本身就是为了解决问题而产生。将数学理论知识应用于农业发展是人类发展史的一大创新，而其中数学期望的概念应用于现代农业，从理论的角度可以推测出方案能够实现的效果，以及可能存在的风险。再结合实际生产的各种情况进行综合考虑，选定最佳的生产方案，实现最优化的经济收入。在这个过程中，可以将一些看似随机、没有规律的随机事件抽象出来，发现事件间的内在关联，发现其潜在的内在规律，为以后农业的发展计划安排、农业的生产、农业的效益等提供积极的预测指导作用。

3 数学期望在农业生产中的应用案例分析

数学期望与方差在农业生产中有着广泛的应用。文章选取几个典型案例来分析说明数学期望在农业生产中的应用。

案例1：一个农场要种植水果，要在苹果、梨或葡萄选一种。根据过去的经验可知，天气干旱、天气正常、天气多雨的概率分别为0.3、0.5、0.2。每种农作物在3种天气下获利情况见表1。该农场种植何作物才能获得最大利润（万元）？

表1　三种水果收益表

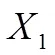
苹果、梨、葡萄3种水果收益的数学期望分别为：

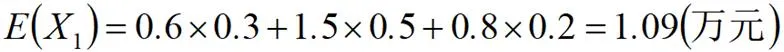
可看到，种植苹果平均收益最大，种植葡萄平均收益最小。所以农场选择种植苹果可获得最大利润。

案例2：某农场拟投资2个项目：种植西红柿和大蒜，其收益受市场行情影响。市场行情可划分为好、中、差3个等级，已知其发生的概率分别为0.3、0.5、0.2。在对应行情下，种植西红柿的收益X（万元）分别为10、8、-4，种植大蒜的收益Y（万元）分别为9、6、-2，详情见表2。该农场应该种植西红柿还是大蒜？

表2　西红柿与大蒜的收益表

分析：要确定农场种植哪种农作物，可以结合利润和风险两部分来考虑。先看数学期望。

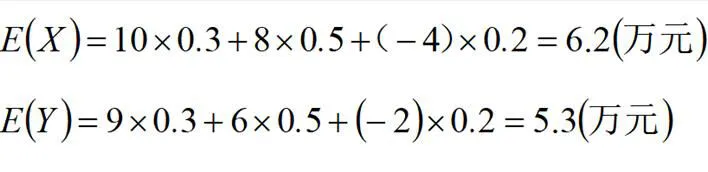
可以看到种植西红柿的利润要高于种植大蒜的利润。

风险需要结合另一个重要概念——方差，进行分析。

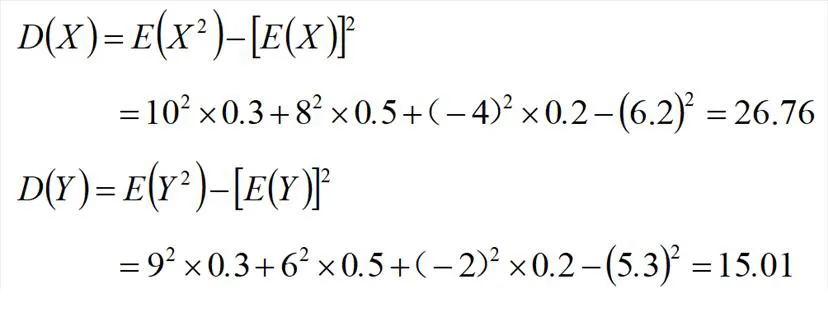
方差越大，收益的波动越大，也就意味着风险越大。

所以如果农场主具有冒险精神，敢于承担风险，追求最大利润的话，可以选择种植西红柿。如果农场主相对保守，追求稳定，可以选择种植大蒜。

由以上两个案例可以看到，可以利用求解对应的数学期望来解决种植哪种农作物的决策问题。有了这样的理论依托，就能在种植前对农作物的情况有大致的了解，确定种植哪种农作物能产生最大的经济效益，从而确定种植哪种农作物。

案例3：某农业基地种植某种黄瓜，已知黄瓜的市场需求量服从（500，800）上的均匀分布。每售出1 t黄瓜，基地利润2万元；若滞销，基地每吨亏损0.5万元。问该农业基地应该种植这种蔬菜多少吨才能使收益最大？

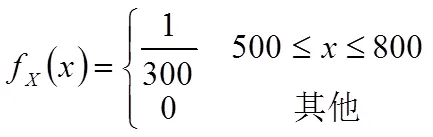
设农场种植黄瓜吨，收益为，则由题意可知

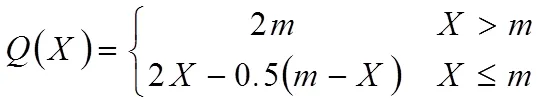
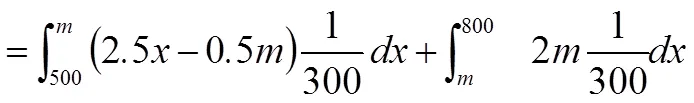
所以，该农业基地应该种植740 t黄瓜才能使收益最大。

由案例3可以看到，通过对期望收益最大化的求解，可以判断出农作物最合适的种植产量。这样既节省了时间，减少了不必要的投入，同时又增加了收入。这也体现了数学期望对农业发展规模的决策指导功能。

案例4：已知甲乙两种冬小麦实验品种连续5年的单位面积产量。如表3所示，试分析哪个品种更值得推广？

表3　甲乙两种小麦的产量（单位：t / km2）

分析：需要确定哪个品种更值得推广，需要考虑小麦的产量和稳定性。

通过求解数学期望，可分别求得甲乙两个品种小麦的平均产量。

设甲乙两种小麦的产量分别是，，

可以看出甲乙两个品种小麦的均产量是相等的。

接下来考虑小麦产量的稳定性。小麦的稳定性可通过两个随机变量的方差来确定。

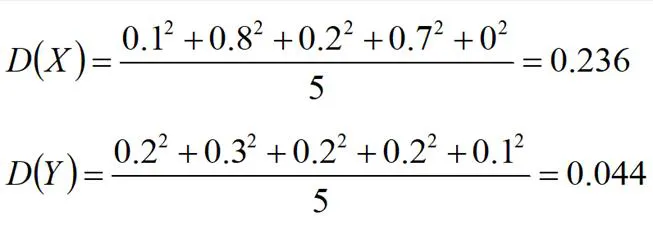
方差越小，小麦产量越稳定。甲种小麦的稳定性明显低于乙种小麦。所以综合考虑均产量和稳定性之后，确定可以推广乙种小麦。

案例4集中体现了数学期望和方差在农业生产中对农产品的选择优化的决策指导作用。由此就可以在种植前通过数据分析筛选优良品种，从而提高农产品的产量，加速现代化农业的发展。

4 小结

文章只是简单介绍了数学期望在农业中的几点应用，但其实数学期望在农业生产中的应用远不仅如此。可以说整个农业生产过程，从种植前选种到农作物收获，都可以用到数学期望来进行预测指导。而且现在国家已经出台了农业保险，农业保险也是与数学期望息息相关的。数学期望在农业中还有更多的应用需要进一步挖掘。现代农业逐渐产业化，数学理论与现代化农业的结合，必然会促进现代化农业更加快速地发展。

[1]张少华.数学期望在农业生产中得应用[J].安徽农业科技,2011,39(16):948.

[2]刘淑芳.概率与数理统计在农业卫生中的应用[J].安徽农业科学,2013,41(3):941-942.

[3]董斌斌.数学期望与方差在实际生产中的应用[J].科技信息:学术版,2011(1):254-255.

[4]陈海能,王文琴.浅谈数学期望在农业生产中的应用[J].农家参谋,2018,579(7):20.

10.3969/j.issn.2095-1205.2020.02.08

S11

A

2095-1205(2020)02-13-02