绕顶转动模式下三维被动土压力的数值研究*

史克宝 卢坤林② 陈一鸣 赵瀚天 尹志凯 石 峰

(①合肥工业大学土木与水利工程学院，合肥 230009，中国) (②安徽工业大学建筑工程学院，马鞍山 243002，中国)

0 引 言

挡土墙上被动土压力的确定是一个经典的土力学问题。二维被动土压力的研究在实际工程中已经得到广泛应用(姚攀峰等，2004；应宏伟等，2016；赵梦怡等，2018)，在理论上也已经使用不同的方法，如极限平衡法(顾慰慈，2005; 秦立科等，2009)、上限极限分析法(高和斌等，2003)、下限极限分析法(Kérisel et al.，1990)。但在现实工程中，许多挡土结构物都以三维的方式产生被动土压力，例如深基坑中支撑结构物挡土墙、边坡预应力的锚杆式支护结构、拱形构筑物的局部支护结构、承受水平荷载作用下的支护挡墙，这些挡土结构物上的被动土压力显著大于经典土压力的计算值，具有明显的三维空间效应(Duncan et al.，2001)。为了保证挡土结构物安全和经济设计的需要，应按空间问题来研究挡土结构物上的被动土压力。

目前，已有相关学者就三维被动土压力开展了相应研究。Horn(1972)进行了三维被动土压力的模型试验研究，总结并提出了挡土墙上三维被动土压力的组成；Soubra et al. (2000)采用上限分析的方法计算出不同参数条件下三维被动土压力系数；krabl et al. (2005)在满足运动许可的条件下，构造了旋转双曲线的空间破坏模式，且利用上限分析法计算空间效应下的被动土压力系数；Benmebarek et al. (2008)采用数值模拟技术研究了平移模式下三维被动土压力的空间效应系数数值解，并与极限平衡解、上限解和试验成果相印证，给出了不同参数下的空间效应系数。

上述这些三维被动土压力的研究均基于挡土墙的位移模式为平移模式(T位移模式)，而其他位移模式(徐日庆等，2002；卢坤林等，2011)下的三维被动土压力的研究甚少。因此，本文拟开展挡土墙绕顶转动位移模式(RT位移模式)(龚慈等，2006)下，无黏性土体挡土墙上三维被动土压力系数及墙后土体滑裂面的研究。

1 数值计算过程

1.1 模型的建立

挡土墙后土体达到极限状态时，挡土墙宽度的减小，会造成挡土墙上被动土压力的增加。本文采用的是有限差分代码FLAC3D软件(Itasca，2000)。利用显式的有限差分程序来数值研究三维条件下连续介质达到平衡或稳定塑性流动时的极限状态(Benmebarek et al.，2008)。研究有限宽深比的刚性挡土墙上三维被动土压力和空间滑裂面。建立模型时把刚性挡土墙中的一面与土体进行接触。考虑到模型建立的对称性，取整体结构的1/4建立数学模型，如图 1所示。其中，b为挡土墙的宽度，h为挡土墙的高度。

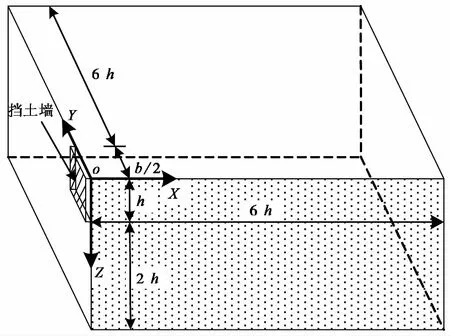
图 1 FLAC3D-1/4对称数学模型Fig. 1 FLAC3D-1/4isymmetrical mathematical model

图2a显示了挡土墙在水平方向施加的速度梯度场，图2b显示了模型中的网格尺寸划分。参照Antão et al. (2011)模型建立的依据，在变形集中的墙土接触面处加密网格单元数量。这是由于变形集中位置处的网格单元数量越多，挡土墙上三维被动土压力系数Kpγ(3D)(Benmebarek et al.，2008)的获取就越精确。

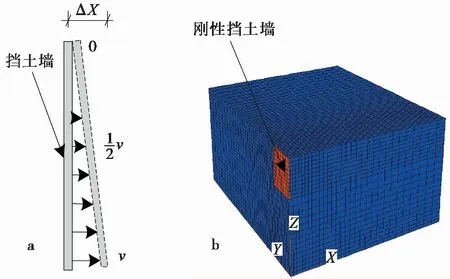
图 2 RT位移模式下网格模型示意图Fig. 2 Schematic diagram of grid model in RT modea. 挡土墙的水平速度场；b. FLAC3D 生成的网格模型

1.2 模型的分析

由于模型尺寸会对数值计算结果产生影响，因此建立模型时，考虑到不同参数条件下，墙后土体滑裂面的大小，除去挡土墙自身的宽度和高度，土体模型为：X方向与Y方向模型尺寸设置为6h，Z方向模型尺寸设置为2ih。模型的边界条件为：X=0和X=6ih界面处固定X方向的移动，Y=0和Y=(6h+b/2)界面处固定Y方向的移动，Z=0界面处固定Z方向的移动。

在挡土墙与土体接触处建立接触面本构模型(陈育民等，2008)，接触面本构模型是由线性库仑剪切强度标准定义的。接触面单元是由许多的三角形单元组成，接触面单元和实体单元通过接触面节点建立联系，每个接触面节点都可以由相关面积进行表示(图 3a)。

在图 3b中，挡土墙与土体接触面的应力-应变关系可用接触面本构模型的元件示意图表示，具体描述如下：

Fn=knμnA

(1)

Fs=ksμsA

(2)

式中：Fn为接触面的法向力矢量(N)；Fs为接触面的切向力矢量(N)；μn为接触面节点法向绝对位移量(m)；μs为接触面剪切相对位移增量(m)；kn为接触单元的法向刚度(N·m-3)；ks为接触面单元的切向刚度(N·m-3)；A为接触面节点代表的面积(m2)。

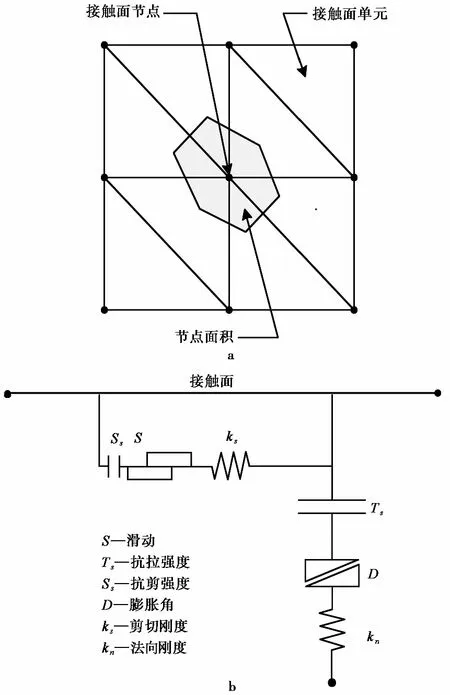
图 3 接触面本构模型示意图Fig. 3 Schematic diagram of constitutive model about the interfacea. 接触面节点面积；b. 接触面本构模型元件示意图

1.3 基本假定

(1)假设挡土墙为绝对刚性体，挡土墙在移动过程中不发生变形。

(2)假设墙后土体是均匀及各向同性的材料，遵从莫尔-库仑屈服准则(李广信等，2008)，且土体没有黏聚力。

(3)模型建立中，挡土墙垂直放置，墙后土体的顶表面为水平面。

(4)墙与土体接触面的摩擦角大小不随挡土墙的移动而发生改变。

(5)挡土墙的移动距离达到一定程度时，墙后土体形成稳定的塑性流动状态。

1.4 计算方案及参数

为了研究模型中挡土墙的宽深比(b/h)、土体的内摩擦角(φ)以及墙土接触面处的摩擦角比值(δ/φ)对挡土墙上三维被动土压力系数及墙后土体滑裂面的影响，本次数值模拟采用的是在不同参数条件下，定向改变其中某一参数来分析该参数对研究结果的影响。因此，模型中6种不同的土体内摩擦角值(φ)和5种不同的墙土接触面摩擦角比值(δ/φ)被考虑。各种参数汇总如下(表 1)。

表 1 数值建模中的参数汇总Table1 Parameter summary in numerical modeling

模型参数的取值范围挡土墙宽深比b/h=0.5、1、2、5、10土体内摩擦角ϕ=15°、20°、25°、30°、35°、40°墙土接触面摩擦角比值δ/ϕ=0、1/3、1/2、2/3、1

(1)接触面单元的法向刚度Kn=109iPa·m-1，剪切刚度Ks=109iPa·m-1。

(2)土体剪切模量G=22iMPa，土体体积模量K=60iMPa，土体重度γ=20ikN·m-3，土体剪胀角ψ=φ。在无黏性土体中，土体剪胀角ψ的变化会对挡土墙上土压力值变化产生影响，本文研究的重点是挡土墙的宽深比(b/h)、土体内摩擦角(φ)及墙土接触面摩擦角比值(δ/φ)对挡土墙上三维被动土压力的影响，土体剪胀角ψ的变化(孔位学等，2009)将是探讨该3种参数后下一阶段的研究重点之一。

1.5 运算过程

(1)模型初始建立过程中，由于土体自重应力和挡土墙的额外刚度作用下，需运算一定的步数使得模型的最大不平衡力达到FLAC3D默认的收敛标准(陈育民等，2008)。达到平衡后，使模型单元返回到初始状态，使得模型处于平衡状态。

(2)RT位移模式下(龚慈等，2006)，由于FLAC3D计算(Itasca，2000)过程中得到的被动土压力误差值取决于挡土墙上所施加的速度场，因此通过将挡土墙壁面速度的减小可以获取更为精确的被动土压力值(Benmebarek et al.，2008)，继而达到新的稳定塑性流动状态。特别对于土体内摩擦角和界面处摩擦角比值较大土体，FLAC3D的计算过程可以重复设置挡土墙的不同速度大小，直到稳态塑性流动状态下的挡土墙上被动土压力之间的计算误差变得可以忽略不计。

1.6 判别依据

本文数值模拟采用剪切应变速率云图(Contour of Shear Strain Rate)来观察挡土墙后土体的滑裂面形成，且用fish函数功能(陈育民等，2008)记录与挡土墙接触的所有土体单元水平方向被动土压力值，观察水平方向被动土压力的发展情况。用此种方法的依据：①剪切应变速率云图可以显示出墙后土体的塑性变形过程及塑性屈服区域(Itasca，2000)，用其分析滑裂面的形成是合理的，从而可以判断墙后土体是否达到了极限状态；②挡土墙在移动过程中，与之接触的土体单元水平方向被动土压力不断增加，墙后土体中的塑性屈服区域不断发展，当墙后土体滑裂面的塑性屈服区域发生贯通并稳定时，用fish函数记录的挡土墙上的水平被动土压力基本都达到最大值，因此用fish函数功能获得的水平方向被动土压力来描述挡土墙上三维被动土压力系数是可行的。

2 数值结果分析

2.1 土体空间滑裂面

在RT位移模式下，当数值计算完成后，沿Z轴负方向观察墙后土体最大剪切应变速率云图，即为挡土墙后滑裂面在主平面上的形态；沿Y轴正方向观察墙后土体最大剪切应变速率云图，即为挡土墙后滑裂面在侧平面上的形态。取最大剪切应变速率云图的中间位置，视为墙后土体滑裂面的边界线(杨山奇等，2018)，如图 4所示。对于b/h=5和b/h=1两种情况下，提取了模型中墙后土体滑裂面在主平面和侧平面上的边界线坐标，绘制墙后土体滑裂面在主平面和侧平面上的形态(图 5)。观察挡土墙后土体的滑裂面形态和滑裂面大小，分析模型中各参数对挡土墙后土体滑裂面的影响。

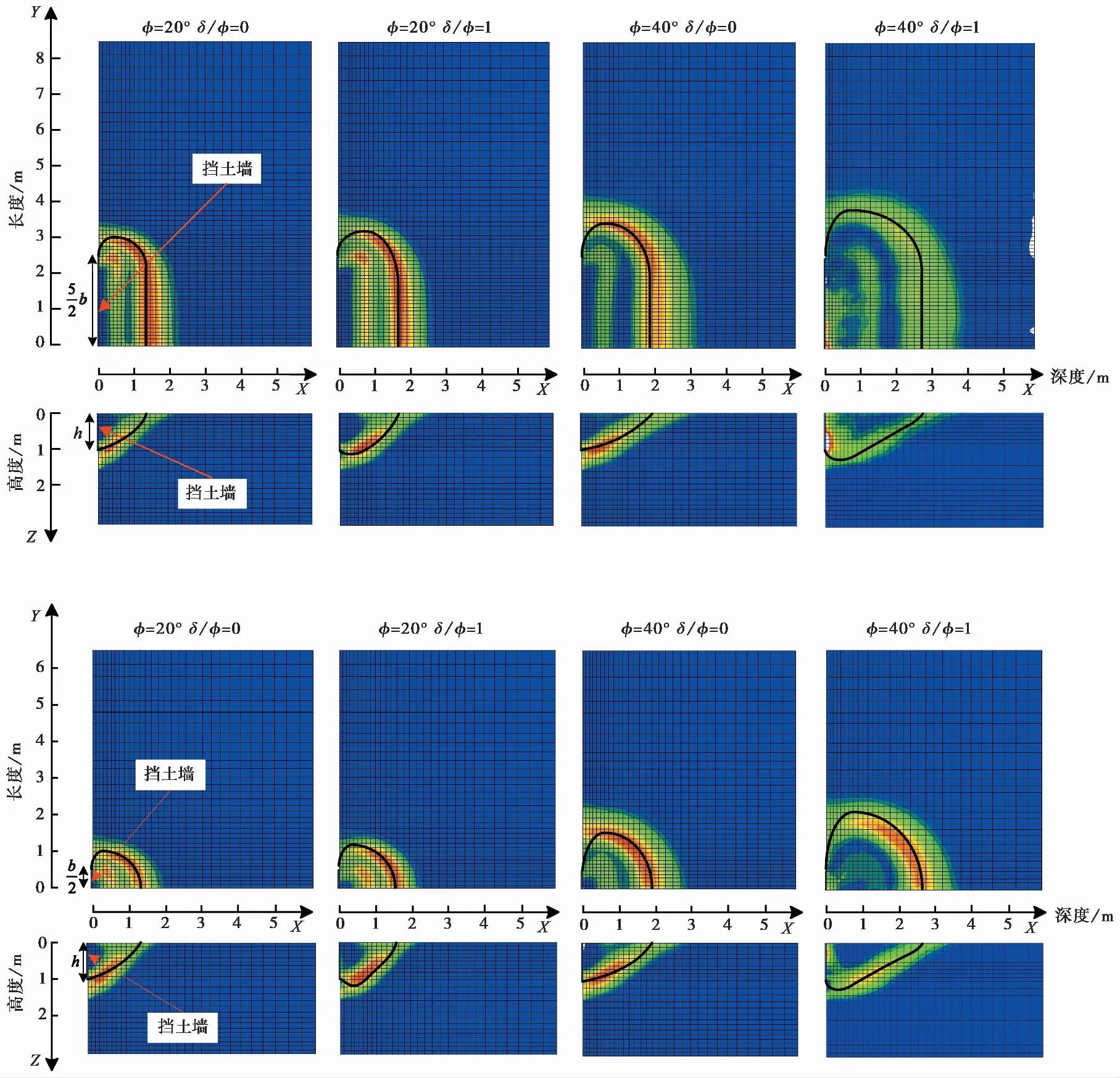
图 4 RT位移模式下挡土墙后土体的剪切应变速率云图Fig. 4 Shear strain rate clouds of soil after retaining wall in RT mode

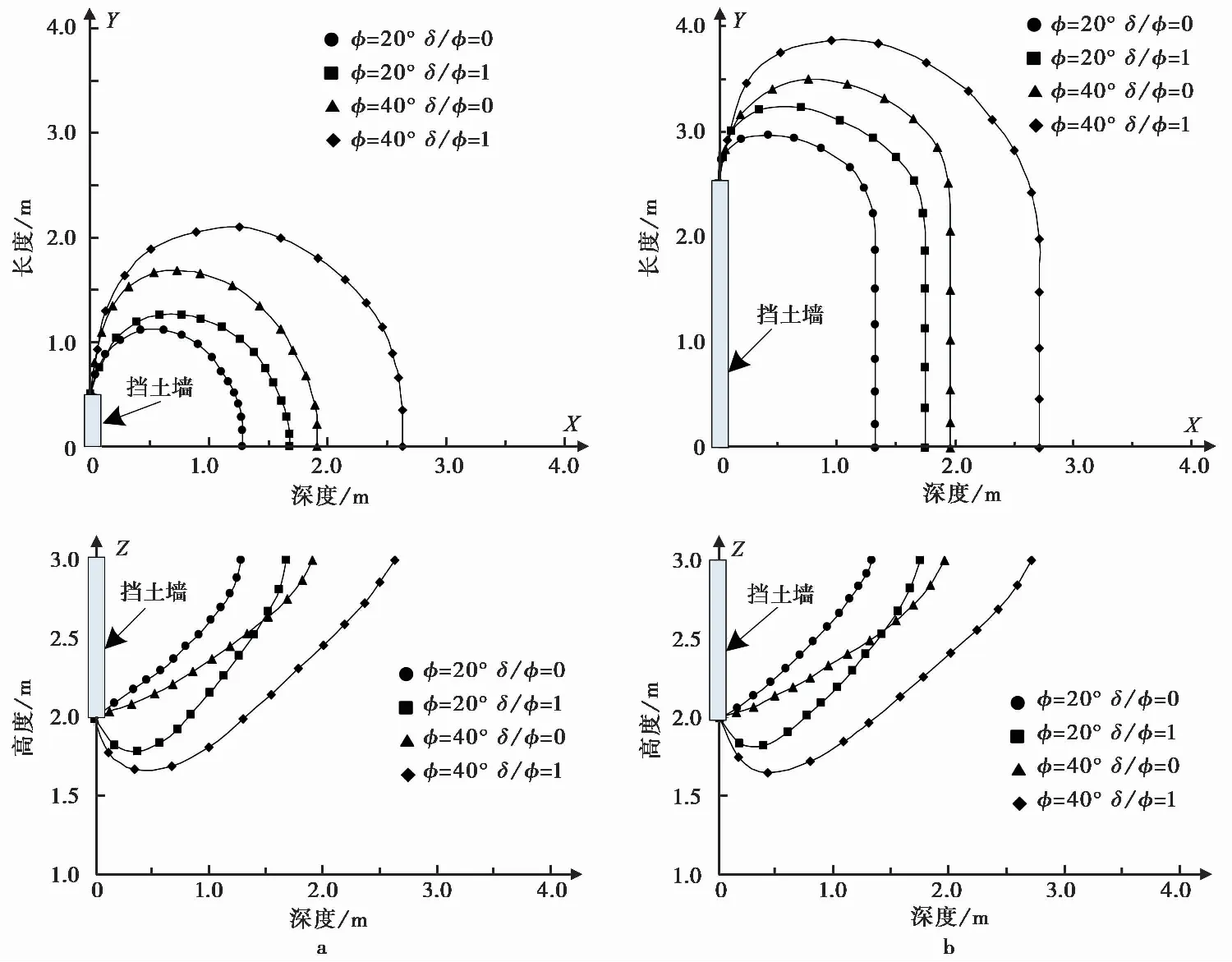
图 5 RT位移模式挡土墙后土体的滑裂面Fig. 5 The spatial slip surface of soil behind retaining wall in RT modea. 挡土墙宽深比b/h=1；b. 挡土墙宽深比b/h=5

由图 5可得到，在挡土墙宽深比b/h=1时，墙后土体滑裂面的主平面形态随X轴方向坐标值的增大呈弧线往外发展后逐渐收敛；在挡土墙宽深比b/h=5时，墙后土体滑裂面的主平面形态随X轴方向坐标值的增大先呈弧线往外发展后逐渐收敛，最远处位置为平行于挡土墙的直线。说明了随着挡土墙宽深比b/h的增加，墙后土体滑裂面的主平面形态由开始的弧线形态逐渐转变为弧线加直线形态。Blum(1932)假设了墙土接触面处为光滑的，基于库仑假设的基础上，认为墙后土体的主平面形态随X轴方向坐标值的增大为先沿某一斜直线往外扩散，达到最远处位置为平行于挡土墙的直线。而本文墙土接触面处为光滑和粗糙两种情况。因此，本文获得的墙后土体滑裂面在主平面上的形态与Blum(1932)假设的主平面形态有一些差别。在墙土接触面处摩擦角比值δ/φ=0时，墙后土体滑裂面的侧平面形态随X轴方向坐标值的增大是从挡土墙的底部沿斜直线的方式往上发展。这同库仑被动土压力造成的墙后土体破坏，形成滑动楔体基本相同。在墙土接触面处摩擦角比值δ/φ=1时，墙后土体滑裂面的侧平面形态随X轴方向坐标值的增大是从挡土墙的底部先沿弧线的方式往上发展，后沿斜直线的方式继续上升(Tejchman et al.，2011)。并且在上述两种情况下时，当滑裂面的侧平面形态将要贯穿土体表面时，滑裂面的斜直线发生偏转。说明了随着墙土触面处摩擦角比值δ/φ的增加，墙后底部土体滑裂面的侧平面形态由斜直线形态逐渐转变为弧线形态，并且也得出了挡土墙的位移模式也会对墙后土体滑裂面形态产生影响。

在挡土墙宽深比b/h=1时，对于模型中土体内摩擦角和墙土接触面摩擦角比值分别为φ=20°，δ/φ=0；φ=20°，δ/φ=1；φ=40°，δ/φ=0；φ=40°，δ/φ=1的4种情况，墙后土体滑裂面在主平面上形态的最大宽度分别为1.1im、1.25im、1.68im和2.1im。与挡土墙宽度b的比值分别为2.2倍、2.5倍、3.36倍和4.2倍；墙后土体滑裂面与挡土墙的最远距离分别为1.28im、1.68im、1.91im和2.62im，与挡土墙高度h的比值分别为1.28倍、1.68倍、1.91倍和2.62倍。同理在挡土墙宽深比b/h=5时，墙后土体滑裂面在主平面上形态的最大宽度分别为3im、3.15im、3.5im和3.86im，与挡土墙宽度b的比值分别为1.2倍、1.26倍、1.42倍和1.544倍；墙后土体滑裂面与挡土墙的最远距离分别为1.33im、1.75im、1.96im和2.71im，与挡土墙高度h的比值分别为1.33倍、1.75倍、1.96倍和2.71倍。可以得出土体内摩擦角φ及墙土接触面摩擦角比值δ/φ均对墙后土体空间滑裂面的范围产生影响，两者之间存在相互联系。且随着挡土墙宽深比b/h的增大，墙后土体主平面上滑裂面形态宽度与挡土墙宽度b的比值减小，墙后土体滑裂面最远距离与挡土墙高度h的比值略微增加。

2.2 三维被动土压力系数

在RT位移模式下，当墙后土体滑裂面的塑性屈服区域发生贯通并稳定时，且fish函数记录的水平被动土压力基本达到最大值时，对挡土墙上某一单元面作受力分析。如图 6所示，每个单元面中心位置处水平方向被动土压力值为pxi，垂直于挡土墙单元面中心位置处方向的被动土压力值为pαi，作用于挡土墙上单元面中心位置处被动土压力值为ppi，作用于整个挡土墙上的被动土压力值为Pp。其中挡土墙与竖直方向的夹角为α，墙土接触面摩擦角为δ。

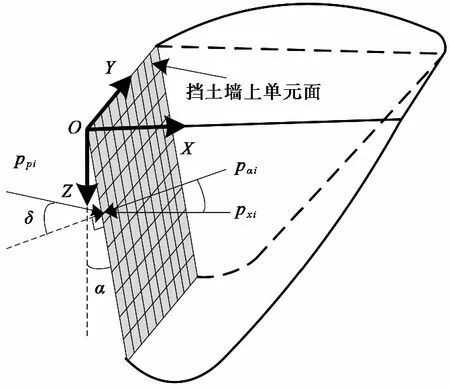
图 6 RT位移模式下挡土墙上单元面受力分析示意图Fig. 6 Schematic diagram of element interface analysis on retaining wall in RT mode

上述被动土压力值之间的关系可以根据下面的公式进行换算(Itasca，2000；Soubra et al.，2000；顾慰慈，2005；Benmebarek et al.，2008)：

pai=pxicosα

(3)

(4)

(5)

对于代表土体重量的三维被动土压力系数Kpγ(3D)，在相同参数条件下，具有黏聚力的土体被无黏聚力的土体(c=0)代替(Benmebarek et al.，2008)，且地面上不存在附加荷载(q=0)情况下，则三维被动土压力系数Kpγ(3D)可以由下述的公式表达：

(n=50，100，……)

(6)

其中，γ表示土体重度；n表示挡土墙上单元的数量(挡土墙上单元的起始数量n可以由挡土墙宽深比进行判断)。

利用上述式(6)完成了对不同参数作用下的刚性挡土墙上三维被动土压力系数Kpγ(3D)的计算，统计挡土墙在RT位移模式下的挡土墙上三维被动土压力系数Kpγ(3D)，如表 2所示。

表 2 RT位移模式下挡土墙上三维被动土压力系数Kpγ(3D)Table2 3D passive earth pressure coefficients Kpγ(3D) on retaining walls in RT mode

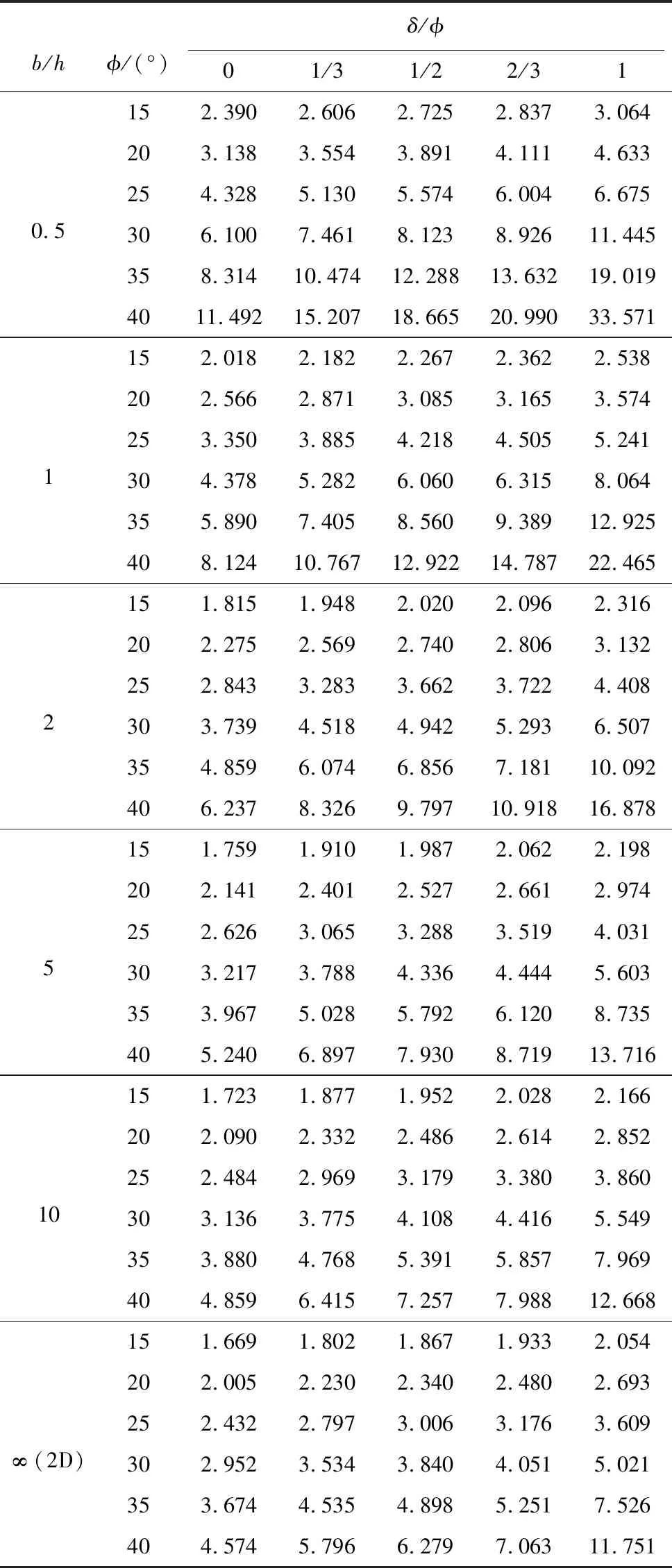
b/hϕ/(°)δ/ϕ01/31/22/310.5152.3902.6062.7252.8373.064203.1383.5543.8914.1114.633254.3285.1305.5746.0046.675306.1007.4618.1238.92611.445358.31410.47412.28813.63219.0194011.49215.20718.66520.99033.5711152.0182.1822.2672.3622.538202.5662.8713.0853.1653.574253.3503.8854.2184.5055.241304.3785.2826.0606.3158.064355.8907.4058.5609.38912.925408.12410.76712.92214.78722.4652151.8151.9482.0202.0962.316202.2752.5692.7402.8063.132252.8433.2833.6623.7224.408303.7394.5184.9425.2936.507354.8596.0746.8567.18110.092406.2378.3269.79710.91816.8785151.7591.9101.9872.0622.198202.1412.4012.5272.6612.974252.6263.0653.2883.5194.031303.2173.7884.3364.4445.603353.9675.0285.7926.1208.735405.2406.8977.9308.71913.71610151.7231.8771.9522.0282.166202.0902.3322.4862.6142.852252.4842.9693.1793.3803.860303.1363.7754.1084.4165.549353.8804.7685.3915.8577.969404.8596.4157.2577.98812.668∞(2D)151.6691.8021.8671.9332.054202.0052.2302.3402.4802.693252.4322.7973.0063.1763.609302.9523.5343.8404.0515.021353.6744.5354.8985.2517.526404.5745.7966.2797.06311.751

2.3 三维被动土压力系数的空间效应

如图 7所示，RT位移模式下，分别显示了挡土墙上三维被动土压力系数Kpγ(3D)随(b/h)、(φ)和(δ/φ)的变化。其中，b/h表示挡土墙自身宽度与深度的比值；φ表示无黏聚力土体中的土体内摩擦角；δ/φ表示墙土接触面摩擦角与土体内摩擦角的比值。分析该3种参数对挡土墙上三维被动土压力系数的影响。

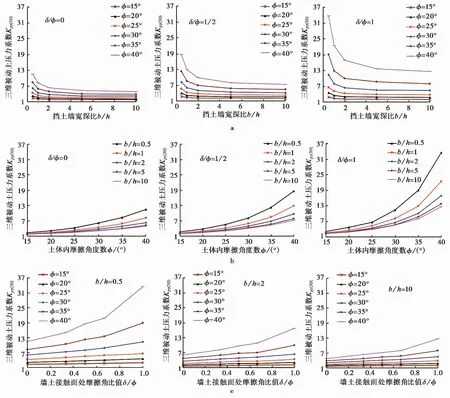
图 7 RT位移模式下挡土墙上三维被动土压力系数Kpγ(3D) 随3种参数变化Fig. 7 3D passive earth pressure coefficients on retaining walls varies with three parameters in RT modea. 随b/h的变化；b. 随φ的变化；c. 随δ/φ的变化

在图 7a中，挡土墙上三维被动土压力系数Kpγ(3D)随着挡土墙宽深比b/h的变大而不断减小，这与Antão et al. (2011)建立的有限单元法的分析结果相一致。且当挡土墙的宽深比b/h大于2时，挡土墙上三维被动土压力系数Kpγ(3D)缓慢减小，而当挡土墙的宽深比b/h小于2时，挡土墙上三维被动土压力系数Kpγ(3D)快速减小，最后趋向于平缓的直线状态。这说明了随着挡土墙宽深比b/h的增大，其对挡土墙上三维被动土压力系数Kpγ(3D)的影响逐渐减小。且通过观察表 2发现，当挡土墙的宽深比b/h等于10时，由于本文篇幅的原因，列举土体内摩擦角等于40°时，挡土墙上三维被动土压力系数Kpγ(3D)分别为4.859、6.415、7.257、7.988、12.668；挡土墙上二维被动土压力系数Kpγ(2D)分别为4.574、5.796、6.279、7.096、11.751。挡土墙上三维被动土压力系数Kpγ(3D)与二维被动土压力系数Kpγ(2D)的比值略微大于1。说明了当挡土墙的宽深比b/h足够大时，挡土墙上三维被动土压力值最终趋向于二维被动土压力值。

在图 7b中，在不同宽深比及墙土接触面摩擦角比值情况时，观察图表中折线的起始位置，可以看出当土体内摩擦角φ较小时，挡土墙上三维被动土压力系数Kpγ(3D)都较小，但随着土体内摩擦角φ的增大，挡土墙上三维被动土压力系数Kpγ(3D)不断增加，且增加的幅度趋向于不断上升。说明了土体内摩擦角φ对挡土墙上三维被动土压力系数Kpγ(3D)的增加具有促进作用，且土体内摩擦角φ会对不同宽深比及墙土接触面摩擦角比值条件下三维被动土压力的空间效应产生相当影响。这与Benmebarek et al. (2008)得出的当挡土墙的宽深比一定时，土体的内摩擦角φ较大时，挡土墙上三维被动土压力的分布具有明显的空间效应相一致。

在图 7c中，通过观察发现，当模型中土体的内摩擦角φ<20°时，挡土墙上三维被动土压力系数Kpγ(3D)的增大随着墙土接触面摩擦角比值δ/φ的增加并不明显。而当模型中土体的内摩擦角φ>30°时，挡土墙上三维被动土压力系数Kpγ(3D)随着墙土接触面摩擦角比值δ/φ的增加而明显增大。从而得出墙土接触面摩擦角比值δ/φ会对挡土墙上三维被动土压力系数Kpγ(3D)产生影响，但要受到模型中土体内摩擦角的限制。

3 RT位移模式与T位移模式的对比

3.1 三维被动土压力系数的对比

表 3给出了RT和T两种位移模式下挡土墙上三维被动土压力系数Kpγ(3D)的大小。其中T位移模式下的挡土墙上三维被动土压力系数大部分是由Benmebarek et al. (2008)通过有限差分代码FLAC3D软件(Itasca，2000)数值模拟获得，对于土体内摩擦角φ=15°和墙土接触面摩擦角比值δ/φ=1/2参数下的挡土墙上三维被动土压力系数Kpγ(3D)，是由本文的数值模型在挡土墙T位移模式下获得的。为了分析RT和T两种位移模式之间三维被动土压力系数差值的变化(Fang et al.，1994)，选取了本文中数值模型的部分参数，对比生成两种位移模式下的挡土墙上三维被动土压力系数Kpγ(3D)的示意图(图 8)。

表 3 RT和T两种位移模式下三维被动土压力系数Kpγ(3D) 的比较Table3 Comparison of 3D passive earth pressure coefficients Kpγ(3D) on retaining walls in RT and T modes

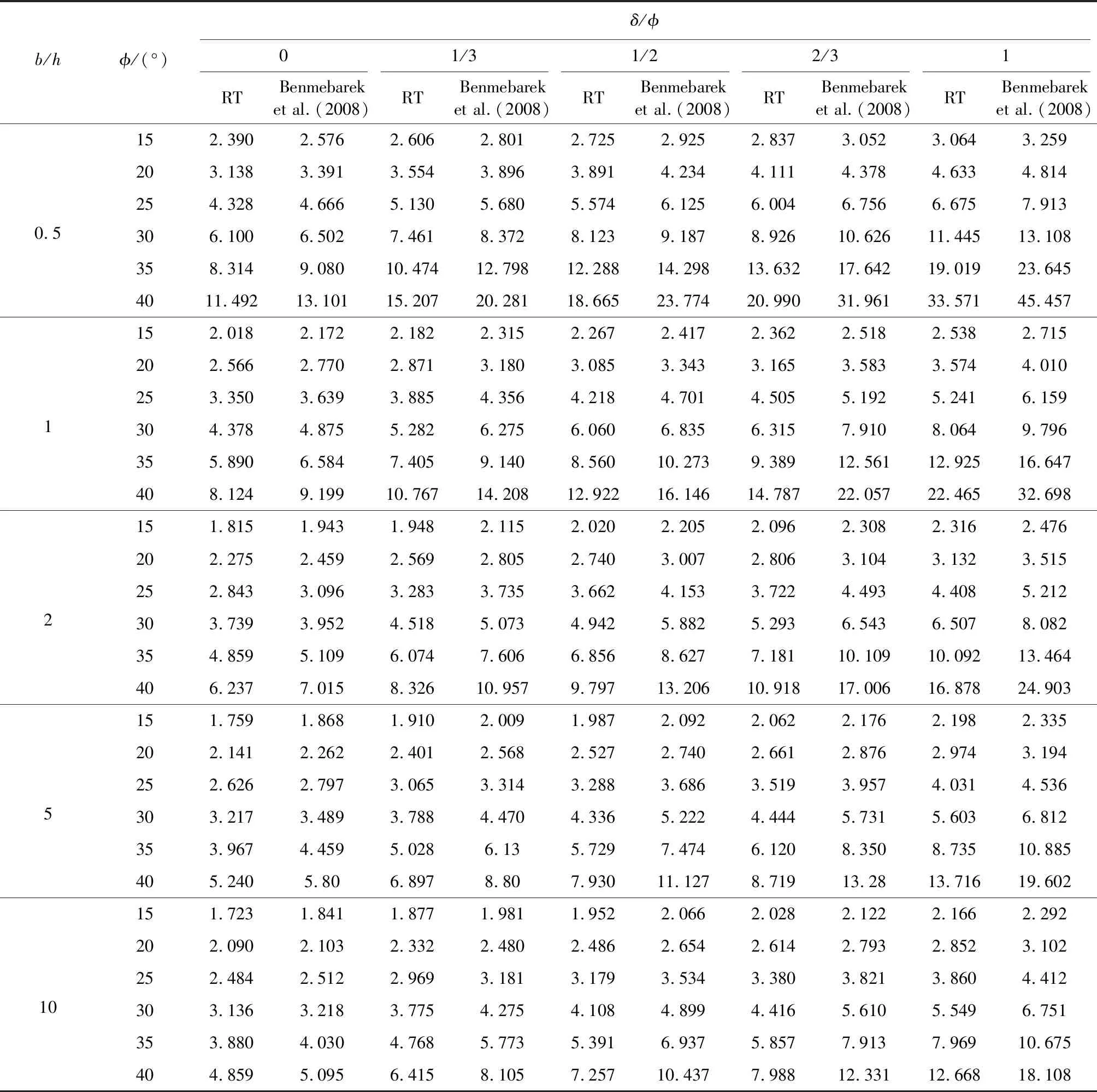
b/hϕ/(°)δ/ϕ01/31/22/31RTBenmebareket al.(2008)RTBenmebareket al.(2008)RTBenmebareket al.(2008)RTBenmebareket al.(2008)RTBenmebareket al.(2008)0.5152.3902.5762.6062.8012.7252.9252.8373.0523.0643.259203.1383.3913.5543.8963.8914.2344.1114.3784.6334.814254.3284.6665.1305.6805.5746.1256.0046.7566.6757.913306.1006.5027.4618.3728.1239.1878.92610.62611.44513.108358.3149.08010.47412.79812.28814.29813.63217.64219.01923.6454011.49213.10115.20720.28118.66523.77420.99031.96133.57145.4571152.0182.1722.1822.3152.2672.4172.3622.5182.5382.715202.5662.7702.8713.1803.0853.3433.1653.5833.5744.010253.3503.6393.8854.3564.2184.7014.5055.1925.2416.159304.3784.8755.2826.2756.0606.8356.3157.9108.0649.796355.8906.5847.4059.1408.56010.2739.38912.56112.92516.647408.1249.19910.76714.20812.92216.14614.78722.05722.46532.6982151.8151.9431.9482.1152.0202.2052.0962.3082.3162.476202.2752.4592.5692.8052.7403.0072.8063.1043.1323.515252.8433.0963.2833.7353.6624.1533.7224.4934.4085.212303.7393.9524.5185.0734.9425.8825.2936.5436.5078.082354.8595.1096.0747.6066.8568.6277.18110.10910.09213.464406.2377.0158.32610.9579.79713.20610.91817.00616.87824.9035151.7591.8681.9102.0091.9872.0922.0622.1762.1982.335202.1412.2622.4012.5682.5272.7402.6612.8762.9743.194252.6262.7973.0653.3143.2883.6863.5193.9574.0314.536303.2173.4893.7884.4704.3365.2224.4445.7315.6036.812353.9674.4595.0286.135.7297.4746.1208.3508.73510.885405.2405.806.8978.807.93011.1278.71913.2813.71619.60210151.7231.8411.8771.9811.9522.0662.0282.1222.1662.292202.0902.1032.3322.4802.4862.6542.6142.7932.8523.102252.4842.5122.9693.1813.1793.5343.3803.8213.8604.412303.1363.2183.7754.2754.1084.8994.4165.6105.5496.751353.8804.0304.7685.7735.3916.9375.8577.9137.96910.675404.8595.0956.4158.1057.25710.4377.98812.33112.66818.108

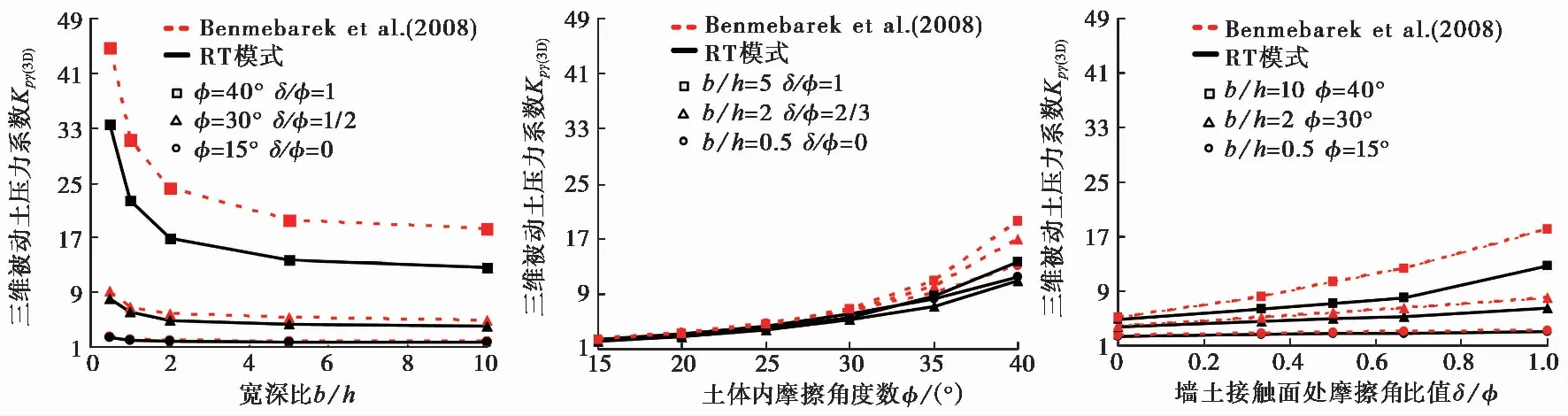
图 8 RT与T两种位移模式下挡土墙上三维被动土压力系数Kpγ(3D) 的对比示意图Fig. 8 Schematic diagram of comparing 3D passive earth pressure coefficients Kpγ(3D) on retaining wall in RT and T modes

结合表 3和图 8得出，当土体内摩擦角和墙土接触面摩擦角比值相同的条件下，例如在φ=15°，δ/φ=0；φ=30°，δ/φ=1/2；φ=40°，δ/φ=1 3种情况时，RT位移模式和T位移模式两者之间的三维被动土压力系数的差值分别为0.186、0.154、0.128、0.109、0.118；1.064、0.975、0.94、0.886、0.791；11.886、10.233、8.025、5.886、5.44。从中可以看出RT位移模式下挡土墙上三维被动土压力系数Kpγ(3D)总是小于T位移模式下挡土墙上三维被动土压力系数Kpγ(3D)。并且两种位移模式下三维被动土压力系数的差值，随挡土墙宽深比b/h的增大而逐渐减小。可见挡土墙的宽深比b/h对两种位移模式之间的三维被动土压力系数的差值影响，随着挡土墙宽深比b/h的增大而不断减弱。

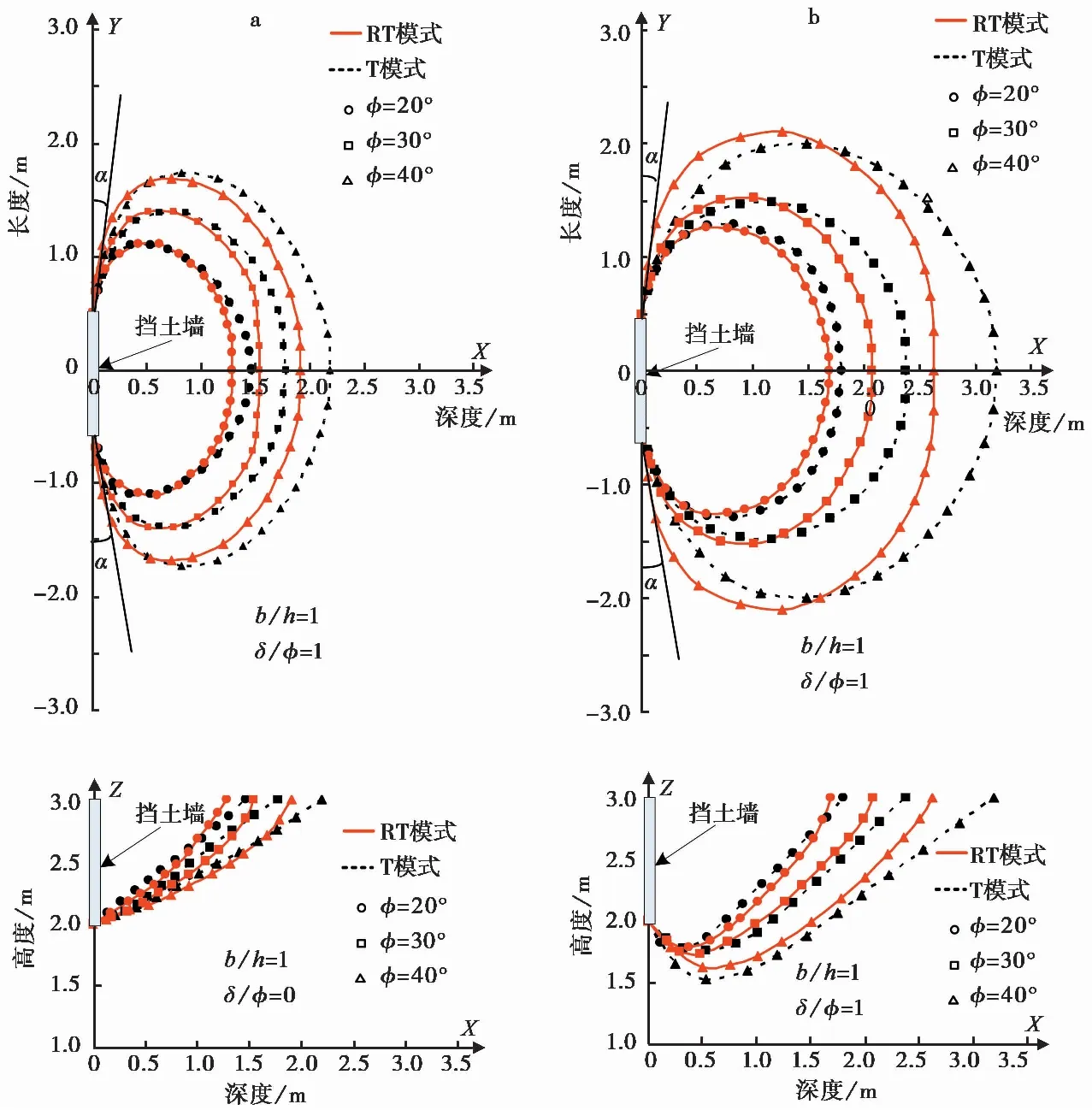
图 9 RT和T两种模式下挡土墙后土体空间滑裂面比较Fig. 9 Comparison of spatial slip surfaces behind retaining wall in RT and T modesa. b/h=1，φ=20°、φ=30°、φ=40°，δ/φ=0；b. b/h=1，φ=20°、φ=30°、φ=40°，δ/φ=1

当挡土墙的宽深比和墙土接触面摩擦角比值相同的条件下，例如b/h=0.5，δ/φ=0；b/h=2，δ/φ=2/3；b/h=5，δ/φ=1 3种情况时，RT位移模式和T位移模式两者之间的三维被动土压力系数的差值分别为0.186、0.253、0.338、0.402、0.766、1.609；0.212、0.298、0.771、1.25、2.928、6.008；0.137、0.22、0.505、1.239、2.15、5.886。从中看出两种位移模式下三维被动土压力系数的差值随着土体内摩擦角φ的变大而不断增加，且增加的幅度趋向不断上升。可见土体内摩擦角φ对两种位移模式之间的三维被动土压力系数差值影响是显著的。

当挡土墙的宽深比和土体摩擦角相同的条件下，例如b/h=0.5，φ=15°；b/h=2，φ=30°；b/h=10，φ=40° 3种情况时，RT位移模式和T位移模式两者之间的三维被动土压力系数的差值分别为0.186、0.195、0.2、0.215、0.195；0.213、0.555、0.94、1.25、1.575；0.236、1.69、3.18、4.343、5.44。从中可以看出两种位移模式下三维被动土压力系数的差值随着墙土接触面摩擦角比值δ/φ的变大而逐渐增加，但是增加的幅度趋向于先上升后下降。

观察表 3数据，选取挡土墙的任意宽深比，对比发现土体内摩擦φ影响下的两种位移模式间的三维被动土压力系数差值的变化幅度明显大于墙土接触面摩擦角比值δ/φ影响下的变化幅度，可见墙土接触面摩擦角比值δ/φ对两种位移模式之间的三维被动土压力系数差值的影响比土体内摩擦角φ的影响较为次之。

3.2 挡土墙后土体空间滑裂面的对比

在RT和T两种位移模式下，数值模拟获得了墙后土体空间滑裂面的对比图(图 9)。其中图 9a显示了墙后土体滑裂面在主平面上的形态，图 9b显示了墙后土体滑裂面在侧平面上的形态。观察墙后土体空间滑裂面的形态和大小，拟选取参数为b/h=1，φ=20°、φ=30°、φ=40°，δ/φ=0和b/h=1，φ=20°、φ=30°、φ=40°，δ/φ=1的两种情况，来对两种位移模式下的墙后土体空间滑裂面的相似处和差异处进行分析和总结。其中，α为墙后土体滑裂面在主平面上的起始扩散角。

由图 9观察，在RT和T两种位移模式下，当土体内摩擦角比值δ/φ=0时，墙后土体滑裂面在主平面上的形态都基本先沿弧线的方式往外扩展，后逐渐收敛。墙后土体滑裂面在侧平面上的形态都基本沿斜直线的方式贯穿土体表面。同理当土体内摩擦角比值δ/φ=1时，墙后土体滑裂面在主平面上的形态基本同δ/φ=0时一致，墙后土体滑裂面在侧平面上的形态都基本先沿弧线往上发展，后沿斜直线的方式贯穿土体表面。但在RT位移模式下(龚慈等，2006)，在主平面形态上，墙后土体滑裂面的起始扩散角α小于T位移模式下的墙后土体滑裂面的起始扩散角α(Soubra et al.，2000)。并且随着墙土接触面摩擦角比值δ/φ的增大，两种位移模式下的扩散角差值不断加大，两种位移模式下的墙后土体滑裂面的宽度大小基本一致。在侧平面形态上，当墙后土体滑裂面将要贯穿土体表面时，墙后土体滑裂面的斜直线发生偏转。其对墙后土体滑裂面的最远处位置影响较大。尤其是当土体内摩擦角φ和墙土接触面摩擦角比值δ/φ都较大的情况下，两种位移模式下的墙后土体滑裂面在主平面上的最远位置的差值就很大。

4 结 论

(1)通过大量的数值计算，总结了RT位移模式下三维被动土压力系数和空间滑裂面形态。

(2)随着挡土墙宽深比b/h的增大，挡土墙上三维被动土压力系数Kpγ(3D)呈先快速减小后缓慢减小的趋势，最后趋于二维被动土压力系数。随着土体内摩擦角φ和墙土接触面摩擦角比值δ/φ的增大，挡土墙上三维被动土压力系数Kpγ(3D)趋不断增加。

(3)挡土墙的宽深比b/h会使得墙后土体滑裂面的主平面形态产生由弧线形态逐渐转变为弧线加直线形态，墙土接触面摩擦角比值δ/φ会使得墙后土体滑裂面的侧平面形态产生由斜直线形态逐渐转变为弧线加斜直线形态。且RT位移模式使得墙后土体表面的滑裂面斜直线发生偏转。土体内摩擦角φ及墙土接触面摩擦角比值δ/φ均会对墙后土体空间滑裂面范围产生影响。

(4)通过对比T和RT两种位移模式，发现位移模式对土压力系数和空间滑裂面形态有着显著的影响。