颗粒形态对砂土抗剪强度影响的试验和离散元数值模拟*

朱 遥 刘 春② 刘 辉 黄靥欢 秦 岩 邓 尚②

(①南京大学地球科学与工程学院，南京 210046，中国) (②南京大学(苏州)高新技术研究院，苏州 215123，中国)

0 引 言

砂土分布广泛，是人类工程建设活动的主要对象之一。抗剪强度是砂土的重要力学指标之一，很多工程实践活动都与砂土的抗剪强度息息相关：如道路地基稳定性问题(王文，2017)、土质边坡稳定性问题、建筑物地基承载能力问题等。因此，分析砂土抗剪强度的影响因素，研究砂土抗剪强度的变化规律，对于指导工程建设以及保障人民群众的生命财产安全有着重大的意义。

黏聚力与内摩擦系数是抗剪强度的评价指标，两者对抗剪强度影响的作用机理有一定差别(蒋明镜等，2009)。C.A.Coulomb提出的抗剪强度表达式认为砂土的黏聚力为0，其抗剪强度主要受到内摩擦力的影响，内摩擦力则是由法向应力以及颗粒间的内摩擦系数所决定的。因此，探求砂土颗粒抗剪强度的影响因素应从砂土颗粒的粗糙程度、颗粒形态、粒径及级配等方面进行考虑(刘熙媛等，2017)。

目前对砂土的颗粒形态的主要研究方式有3种：定量化指标法、试验方法以及计算机模拟法(高金翎，2013)。对于颗粒形态的定量化指标法，Cho et al.(2006)基于球形度、棱角度以及粗糙度3个角度对颗粒形态进行描述；而Bowman et al.(2001)则从数学的角度，采用傅里叶变换以及分析理论对砂土的颗粒形态进行描述，但是砂土的颗粒形态描述理论从单个颗粒描述到群体颗粒描述以及群体颗粒形态的分布特征仍不成熟，颗粒形态的定量化描述目前仍存在着很多的困难。随着计算机技术的发展以及离散元法的出现，室内试验与数值模拟逐步成为了分析砂土颗粒形态的重要手段。

在直剪试验的数值模拟中，最早采用的是弹塑性有限元法(FEM)(Cividini et al.，1992; Tejchman，2005)，但是由于砂土为非连续介质，基于连续介质理论的FEM并不能反映出粒径、颗粒形态等材料参数对模拟结果的影响。因此，基于非连续介质力学的离散元法DEM在颗粒介质的数值模拟中得到了广泛的应用(Mora et al.，1993)。该方法成本低、易操作，非常适用于砂土等离散介质体的数值模拟。与定量化描述法不同，砂土颗粒形态的数值模拟法更加方便快捷，建立合适的离散元模型，结合室内试验和数值模型来进行研究。同时，在宏微观尺度上，利用离散元法模拟岩石力学与土力学试验，可以定量的分析岩土体宏观变形和破坏的微观机制，为探究岩土体宏观力学性质的微观机制提供了一个很好的手段(李世海等，2003，2004；蒋明镜等，2012，2014)。离散元法可以通过重叠和拼合基本的球形单元来拟合不规则的砂粒，来模拟砂土颗粒的不规则形态，可以定量化分析研究颗粒形态对砂土抗剪强度的影响。目前研究砂土抗剪强度的影响因素最常用的手段就是将数值模拟法与室内试验相结合，通过数值模拟法可以探究其微观特性，并采用室内试验来确定模拟结果的准确性。严颖等(2009)对非规则颗粒材料的力学行为进行了离散元数值模拟，并通过碎石料的直剪试验进行了验证；邓雄等(2014)通过离散元法模拟自然条件下断层物质的直剪过程得到断层物质的受压剪切特性；金博等(2015)通过PFC3D软件从刚度、密度、粒径等方面对混合型颗粒材料进行详细的数值模拟分析，获得了详细的力学表征; 乐天呈等(2018)通过室内试验以及离散元软件MatDEM研究了不同级配下砂土的压缩性。

目前，针对颗粒形态对砂土抗剪强度影响的研究已取得了一定的成果，但是数值模拟多局限于二维，且颗粒数量相对较少。基于课题组自主研发的高性能三维离散元数值模拟软件MatDEM(刘春等，2014；Liu et al.，2017)，该软件具备强大的二次开发功能，可以通过二次开发完成复杂的岩土试验数值建模。本文拟对多组球形石英砂以及实验室标准砂进行室内直剪试验，就颗粒形态如何影响砂土抗剪强度进行研究，并基于MatDEM数值模拟得出的结果加以验证。

1 直剪试验

1.1 试验材料、方法和过程

试验材料为球形石英砂和实验室标准砂，均为干燥颗粒，球形石英砂和实验室标准砂按粒径可分为0.6～0.8m、0.8～1.0m、1.0～1.2m、1.4～2.0m以及2.0～2.5m 5个粒组，每一组球形石英砂均对应着一组相同粒组的实验室标准砂。共计10个砂土试样。球形石英砂颗粒表面光滑规整，实验室标准砂为自然采集筛分后的自然石英砂，表面粗糙无规则，且每一组的级配服从正态分布。

本文采用砂雨法制作石英砂试样，试样为圆柱形试样，直径61.8imm，高20imm。制样时石英砂颗粒从漏斗竖直落入下方的直剪盒内，砂样落距均为6icm以保证不同粒径砂样的密度均相同，各粒径试样的自然休止角如表 1、表 2所示，自然休止角不受落距、漏斗直径影响(仇亮等，2019)。

表 1 标准砂自然休止角Table1 Angle of repose of standard sand

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8自然休止角/(°)31.0828.6526.6325.5923.99

表 2 球形石英砂自然休止角Table2 Angle of repose of spherical quartz sand

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8自然休止角/(°)19.8316.9213.6212.0810.84

当颗粒从直剪盒的边缘溢出则立刻停止落砂，并用刀片刮去多余的部分，在上方依次放上滤纸、透水石和传压板。然后在直剪盒上方施加荷载进行直剪试验，参照土工试验规范，以对应快剪的0.8imm·min-1的剪切速度进行剪切，使试样在4imin内剪损，并通过电子千分表测量刚环变形量，从而间接测得剪切过程中的剪应力。为测得砂土的内摩擦系数，每一组试样分别在4级荷载下进行剪切试验，荷载分别为：100kPa、200kPa、300kPa、400kPa。

1.2 剪切特性曲线

以在100ikPa荷载下的剪切特性曲线为例(图 1、图2)，剪切试验过程中，球形石英砂和标准砂的剪切特性曲线变化趋势一致，前期剪应力迅速增加然后逐渐趋于一个定值。试样的抗剪强度为剪切过程中的峰值强度，颗粒形态规则的球形石英砂峰值强度较低，表面形态不规则的标准砂峰值强度较高。在相同的正向压力下，颗粒形态为影响抗剪强度的主要因素，颗粒形态不规则的标准砂试样抗剪强度明显大于球形石英砂试样；同时粒径也影响着抗剪强度，在相同的表面形态条件下，砂土颗粒粒径越大，抗剪强度就越大。

图 1 100ikPa荷载下标准砂剪切特性曲线Fig. 1 Shear characteristic curve of standard sand under 100ikPa load

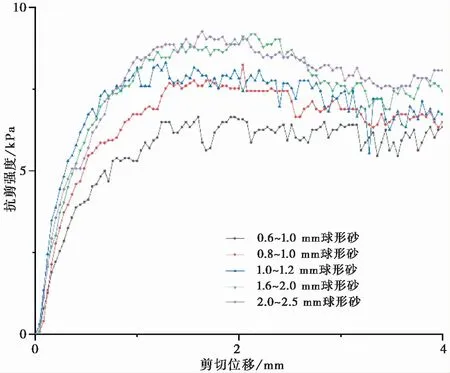
图 2 100ikPa荷载下球形砂剪切特性曲线Fig. 2 Shear characteristic curve of spherical sand under 100ikPa load

从图 1、图 2可以看到，球形石英砂要比实验室标准砂要更快到达峰值强度。其主要原因是颗粒形态为球形的石英砂只需要克服颗粒间的滑动摩擦力，在外部荷载作用下颗粒的旋转和重新排列可以快速完成；而颗粒表面形态不规则的标准砂，表面多棱角，颗粒与颗粒之间会出现相互咬合嵌锁的作用，在外部荷载作用下要完成颗粒的重新排布需要克服颗粒之间的咬合嵌锁作用，故较慢到达剪切峰值强度。试样在200ikPa、300ikPa以及400ikPa的荷载下剪切特性曲线趋势特征与100ikPa荷载下的基本一致。

1.3 抗剪强度和法向应力关系曲线

抗剪强度与法向应力的关系图像是反映颗粒材料性质的一个重要方法，根据Mohr-Coulomb准则，单一试样的剪切峰值强度与正应力成正比，其比例是内摩擦角的正切值。采用最小二乘法(谈云志等，2005)，将试验得到的各试样的抗剪强度与荷载强度拟合，结果如图 3、图 4所示：标准砂拟合直线不过原点，球形石英砂拟合函数基本都为过原点的直线。

直剪试验中，内摩擦角θ=arctank，其中，k为剪切特性曲线的斜率，如表 3、表 4所示，球形石英砂与实验室标准砂的内摩擦系数都随着粒径的变大而变大，并且在相同粒径的条件下，颗粒形态不规则的标准砂的内摩擦系数明显大于球形石英砂的内摩擦系数。

Liu et al.(2017)提出的离散元宏微观系数计算公式：

式中:Fs0为剪应力；μp为颗粒微观的内摩擦系数；Cu为单轴抗压强度;d为颗粒粒径。

该公式指出，粒径越大，剪应力越大，剪应力由初始抗剪强度以及摩擦角决定，砂土初始抗剪强度可以忽略不计，故粒径越大，内摩擦角越大，即内摩擦系数越大，该公式的结论与本次试验得到的结论相同。

图 3 标准砂剪应力与法向应力拟合曲线Fig. 3 Curve of shear stress and normal stress of standard sand

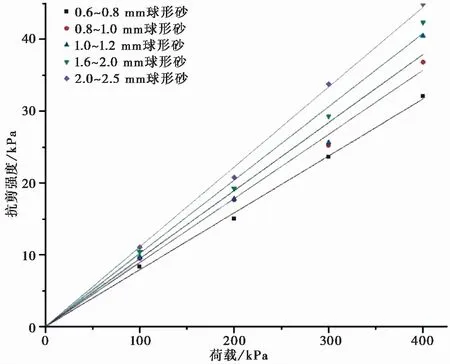
图 4 球形砂剪应力与法向应力拟合曲线Fig. 4 Curve of shear stress and normal stress of spherical sand

表 3 球形石英砂各粒组摩擦角Table3 Friction angle of spherical quartz sand of each group

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8内摩擦系数0.11940.11620.10930.10610.0965摩擦角/(°)6.86.66.26.15.5

表 4 实验室标准砂各粒组摩擦角Table 4 Friction angle of each group of laboratory standard sand

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8内摩擦系数0.19530.18710.18030.16790.1606摩擦角/(°)11.110.610.19.59.1

散体堆积体内部颗粒接触法向量、法向接触力和切向接触力的各向异性强度指标与自然休止角有着明显的正相关性，颗粒形态愈不规则、粒径愈小，颗粒间强度指标与自然休止角愈小(戴北冰等，2019)。结合各试样的自然休止角，可知表面形态不规则的石英砂内部颗粒间作用力明显大于球形石英砂；同时，在拟合各试样剪应力与法向应力拟合曲线发现，标准砂试样的拟合曲线基本上都不过原点，存在着一定的黏聚力，表明颗粒形态不规则的标准砂颗粒之间存在着相互嵌锁作用，从宏观上表现出试样有着一定的黏聚力。

砂土是无黏性的散体材料，影响其抗剪强度的因素主要是颗粒间的滑动摩擦力与咬合摩擦力两部分。当试样为球形石英砂时，其表面颗粒形态为规则的圆球状，颗粒间的摩擦强度较小，其抗剪强度主要体现在其滑动摩擦力；而当试样为实验室标准砂时，其表面颗粒形态不规则且粗糙，颗粒与颗粒之间有着较强的咬合嵌锁作用，滑动摩擦力与咬合摩擦力共同影响着抗剪强度。所以在相同剪切条件下，球形石英砂在外部荷载作用下能更快地完成颗粒的重新排列，且抗剪强度较低，而实验室标准砂则需要克服颗粒间的咬合嵌锁，峰值强度较高。

2 离散元法与MatDEM软件

2.1 离散元基本原理和赫兹模型

离散元法通过堆积和胶结一系列具有特定力学性质的颗粒来构建岩土体模型，并在此基础之上通过时间步的迭代算法来进行数值模拟。通常情况下采用最基本的线弹性模型进行数值模拟，该模型假定颗粒与颗粒直接依靠着弹簧相互接触并产生力的作用。但当颗粒表面光滑无粘连，接触面与总表面积相比极小，接触力垂直于接触面，且仅有弹性形变发生时，单元之间的法向接触力可采用赫兹模型计算。由于球形石英砂为无黏性颗粒。为此，在本文中采用赫兹模型作为石英砂颗粒的基本力学模型(孙其诚等，2009)。

如图 5所示，半径分别为R1、R2的两个单元发生弹性接触，法向重叠量A满足：

A=R1+R2-|r1-r2|≥0

式中：r1、r2分别为两单元的位置矢量。接触面为圆形，其半径a满足：

在离散元法中单元泊松比μ为0，且单元弹性模量E与法向刚度Kn之间存在如下关系：

故法向力Fn为：

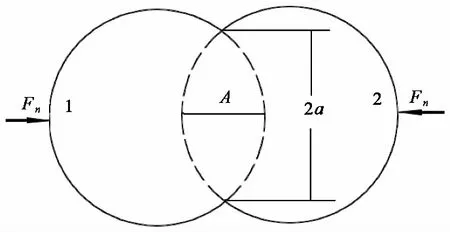
图 5 赫兹接触模型Fig. 5 Hertz contact model

2.2 弹性clump的原理

在进行数值模拟时，对于不规则非球形的石英砂颗粒，可以将多个离散单元相互重叠构成团簇。团簇(clump)是由离散元的基本单元相互交叠而成的不规则颗粒形态的颗粒。故可以在生成模型颗粒时随机构成不规则颗粒，从而实现颗粒形态不规则的实验室标准砂的建模。

如图 6所示：在团簇模型中，单元相互重叠量为l0，单元直径为d，设定颗粒之间的平衡位移为d-l0，两个单元中心之间的距离为s，则相对位移Xn为：

Xn=s-(d-l0)

当两颗粒相对位移Xn为0时，两颗粒处于平衡状态，当Xn增加时，颗粒间产生拉力；当Xn减小时，颗粒间相互挤压，产生斥力，为使得模型在计算过程中体积守恒，clump单元不可被破坏。该模型其本质是将颗粒间的平衡距离减少并在计算位移时减去其初始重叠量(索文斌等，2017)，通过这种方法可以完成复杂模型的建模，建立由多个颗粒单元构成的形态不规则的团簇模型。

图 6 团簇clump示意图Fig. 6 Schematic diagram of the clump

MatDEM所采用的弹性clump单元模型，与传统的刚性clump模型不同，能较好的模拟颗粒形态复杂的单元的变形与破坏。

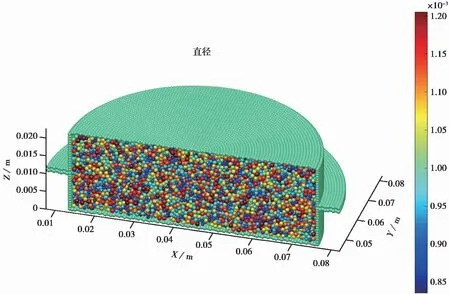
图 7 直剪试验模拟几何模型Fig. 7 Geometric model of direct shear test simulation

2.3 iMatDEM数值建模

矩阵离散元MatDEM(刘春等，2014)是南京大学自主研发的一种岩土体高性能离散元软件，该软件基于矩阵计算以及三维接触模型，创新性的采用了能量守恒原理，极大地提高了运算速度和计算单元数，并提供二次开发平台供使用者完成复杂的数值模拟(朱晨光等，2019)。本文基于MatDEM二次开发功能研发了直剪试验三维离散元模拟器，具体过程如下：

(1)建立几何模型。数值模型由直剪盒和试样组成，其按照真实试验中的试样1︰1还原配比。图 7为粒径0.8～1.0imm球形石英砂的直剪试验模型，该粒径砂样颗粒数为172396。直剪盒由上、下剪切盒构成，其中上直剪盒由上环和上压力板组成，上压力板可移动并能施加荷载。在构建数值模拟砂样时，先设置其平均粒径为0.9imm，调整粒径的分散系数使得砂粒粒径随机分布在0.8～1.0imm，然后使颗粒在重力作用下自然沉积以模拟砂雨法制样，最后将试样放入剪切盒中。

(2)赋予材料性质并加压。MatDEM采用自带的材料训练功能赋予单元颗粒性质从而模拟现实对象。根据Liu et al. (2017)给出的紧密堆积离散元模型单元力学参数与模型整体力学性质之间的解析解，可以将试样的宏观力学参数转化为微观单元力学参数，但随机堆积模型可能将各力学性质降低10%～40%。为此MatDEM开发了材料训练功能：宏观材料性质代入转换公式获得其初始微观参数再乘以一个比值；通过自动的单轴压缩、抗拉强度、抗压强度测试，获得块体的弹性模量和强度；利用实测值和设定值的比率重新调整rate，直至各力学参数收敛于设定值，由此得到的才是最符合实际的微观单元参数。

由于采用的为赫兹模型，材料训练后获得的微观单元参数如表 5所示。

表 5 离散元颗粒微观参数Table5 Microscopic parameters of discrete element particles

微观参数法向刚度Kn/kN·m-1粒间内摩擦系数μp阻尼值2052900.007 13

将材料参数赋予颗粒单元之后施加上覆荷载，通过迭代计算，使试样逐渐被压实，并在荷载作用下达到稳定状态。

(3)剪切过程设置。通过移动下剪切盒进行直剪试验，每移动2×10-4mm则进行一次标准平衡迭代计算，当应力充分消散之后再继续进行下一步加载。下剪切盒移动4imm后停止试验，模拟结果符合预期，颗粒数目最多的一组模拟运行完毕需约10ih。

3 分析与讨论

3.1 试验、模拟结果对比

为验证直剪试验数值模拟的正确性，以粒径为0.8～1.0imm的实验室标准砂与球形石英砂的剪切特性曲线为例(图 8、图 9)，数值模拟的剪切特性曲线变化趋势及抗剪强度与试验结果基本吻合。

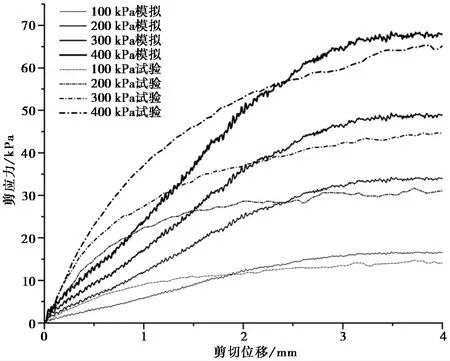
图 8 标准砂试验、模拟对比Fig. 8 Standard sand test and simulation comparison

图 9 球形石英砂试验、模拟对比Fig. 9 Spherical quartz sand test and simulation comparison

但仍存在一定差异，主要原因为：(1)模拟采用的赫兹模型，假定每个离散元单元的泊松比都为0，即当单元受压时只会沿着受力方向产生弹性形变，不产生侧向变形；但真实试验中的颗粒受压时会产生一定的侧向变形，导致了模拟结果存在误差; (2)直剪试验结束后发现有少量石英砂被破坏，而模拟中的球形石英砂与标准砂均为不可破坏的颗粒单元，故模拟与真实试验存在一定的误差。该差异在其他几组的球形石英砂以及实验室标准砂对比中也显著存在。

数值模拟结果如表 6，表 7所示。在颗粒形态相同的情况下粒径越大，试样的内摩擦角就越大，并且，颗粒形态不规则的标准砂的内摩擦角明显大于球形石英砂。这与试验得到的结果相同，进一步验证了离散元数值模拟的可行性。

3.2 位移场分析

位移场的不规律分布意味着颗粒之间重新排列，故可以从位移场的分布来探究球形石英砂与实验室标准砂在直剪过程中剪切带的形成。

表 6 模拟标准砂各粒组摩擦角Table6 Friction angle of simulate standard sand

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8内摩擦系数0.2150.1960.2000.1830.173摩擦角/(°)12.111.111.310.49.8误差/%8.34.511.08.77.4

表 7 模拟球形砂各粒组摩擦角Table7 Friction angle of simulate spherical sand

粒径/mm2.0～2.51.4～2.01.0～1.20.8～1.00.6～0.8内摩擦系数0.1130.1090.1040.0990.094摩擦角/(°)6.46.25.95.75.4误差/%5.75.64.17.02.2

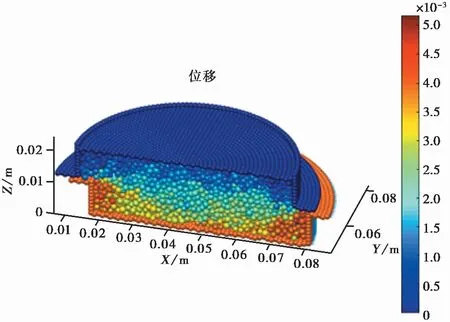
图 10 100ikPa荷载下球形石英砂位移场Fig. 10 Displacement field of spherical quartz sand under 100ikPa load

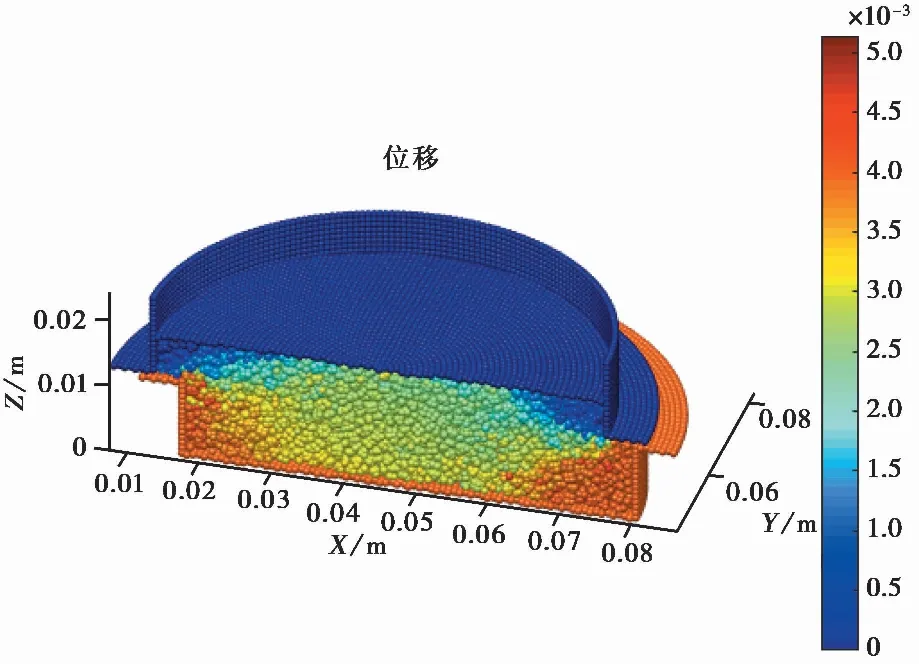
图 11 100ikPa荷载下标准砂位移场Fig. 11 Displacement field of standard sand under 100ikPa load

图 10,图 11为剪切试验模拟结束后球形石英砂颗粒与标准砂颗粒的位移情况。X方向为直剪盒剪切方向，Z方向垂直于上压力板。如图所示，上下直剪盒内的石英砂位移情况形成了非常良好的对称性，中部颗粒的位移距离明显大于周围颗粒的位移距离，故可以认为该处形成剪切带(Frost et al.，2012)，剪切带的形成与模拟预期相符，很好地验证了试验的正确性。可以看到，标准砂的剪切盒中部颗粒位移多为3imm左右，球形石英砂的剪切盒中部颗粒位移多为2imm左右，表明标准砂在直剪盒内的中部颗粒受到下方直剪盒的强制位移的影响比球形石英砂要大，验证了不规则的标准砂颗粒直剪的嵌锁作用这个机制。

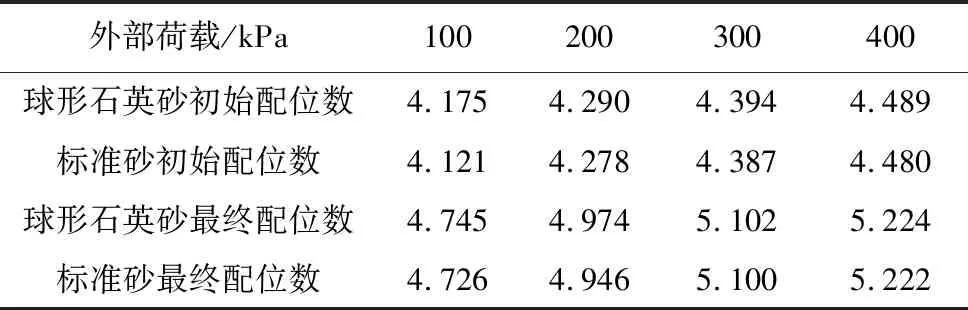
表 8 1.0～1.2 mm粒组石英砂配位数Table8 Coordination number of 1.0～1.2 mm grain group quartz sand

外部荷载/kPa100200300400球形石英砂初始配位数4.1754.2904.3944.489标准砂初始配位数4.1214.2784.3874.480球形石英砂最终配位数4.7454.9745.1025.224标准砂最终配位数4.7264.9465.1005.222

3.3 配位数分析

平均配位数(Ac)是指所有单元接触总数与单元总数的比值，代表着土颗粒的密实程度，其数学表达式为：

式中：Nc为所有单元接触总数；Np为单元总数。

颗粒物质通过颗粒间的接触力来抵抗外部剪切作用，而颗粒间的接触力则与配位数有关，一般来说，试样的配位数越高，试样颗粒堆积越紧密，颗粒间的作用越强(周伟等，2012)，从而导致抗剪强度的提高。所以，在剪切试验中，配位数的变化与剪应力的变化存在着一定的正相关性。

表 8为粒径1.0～1.2imm的球形石英砂与实验室标准砂的初始以及直剪完成之后的配位数。模拟数据表明，颗粒配位数随着上压力板荷载的增加而增加，宏观上表现出外部荷载的增加提高了试样的密实程度；粒径相等的实验室标准砂与球形石英砂的初始和最终配位数基本一致，但是在剪切过程中的配位数变化趋势与各自的模拟剪切特性曲线相似(图 12)，球形石英砂配位数变化曲线较快达到峰值配位数并趋于稳定，而石英砂配位数则较晚达到配位数峰值，该曲线与模拟得到的剪切特性曲线有着良好的对应性，两者拐点所处的剪切位移基本相同。

图 12 100ikPa荷载下1.0～1.2imm粒组试样配位数变化曲线Fig. 12 Coordination curve of 1.0～1.2imm particle group sample under 100ikPa load

在外部剪切作用下试样内颗粒进行重新堆积，球形石英砂能更快地到达稳定配位数，这表明了球形石英砂能够在外部剪切作用下更快地重新排列堆积以到达稳定状态。这主要是因为球形石英砂试样颗粒间摩擦强度较小，其抗剪强度主要体现在滑动摩擦力，在外部荷载作用下能较快完成颗粒的重新排列，从而达到峰值强度。而标准砂的颗粒粗糙不规则，颗粒间多咬合嵌套，故在外部荷载作用下较晚完成颗粒的重新排列到达峰值强度。

4 结 论

通过球形石英砂与实验室标准砂展开的直剪试验与相应的离散元数值模拟，结合剪切特性曲线、位移场以及配位数变化对不同颗粒形态的石英砂抗剪强度进行了分析，得到以下结论：

(1)基于MatDEM二次开发的三维直剪试验模拟器能够有效地进行砂土直剪试验的离散元数值模拟，计算效率高，计算单元数可达上百万，同时能够记录模拟过程中的所有颗粒的受力、位移等单元参数。

(2)试验结果与数值模拟结果相符：自然休止角与抗剪强度有着正相关性，标准砂存在着一定的黏聚力；砂土颗粒粒径越大，抗剪强度越大；相同粒径情况下颗粒形态规则的球形石英砂抗剪强度明显小于颗粒形态不规则的实验室标准砂；球形石英砂较实验室标准砂能更快地到达峰值强度随后趋于稳定。

(3)直剪试验中剪切盒内中部位移较四周颗粒更大，形成了明显的剪切带。标准砂剪切带内颗粒的位移较大，验证了标准砂颗粒嵌锁的机制。

(4)配位数的变化与剪应力有着正相关性，在相同粒径以及剪切条件下，不同颗粒形态的石英砂初始和最终配位数基本一致，但规则形态的球形石英砂能较快达到峰值配位数并随后稳定，而颗粒形态不规则的实验室标准砂则较晚达到峰值强度。