水声干扰器干扰效果参数级建模与分析

庞 博

(海军装备部驻上海地区军事代表局驻上海地区第七军事代表室，上海201108)

0 引 言

水声干扰器作为一种对抗器材，对声呐具有干扰压制作用。当我方舰艇被敌方声呐探测并跟踪后，我方舰艇可释放干扰器，并在干扰器的掩护下迅速远离敌方声呐。本艇机动的原则是在本舰发射干扰器后的压制扇面内，敌方声呐不能对我方舰艇继续探测并实施有效攻击[1-4]。

从水声对抗的作战效能角度出发，计算干扰器对敌方声呐的压制扇面，可以在对抗实施过程中更好地掩护本艇，压制扇面的范围也反映了声干扰器的干扰效果。另一方面，干扰器的作用能够使敌方声呐的作用距离降低甚至致盲。通常评价干扰器的干扰效果以压制扇面和探测距离衰减率为主要指标[5]。

对干扰器干扰效果的评估，理想的方法是将其放在接近实战的环境下进行多次检验。但是，这种方法人力物力的消耗大、费用昂贵；另外，海上环境的条件变化较大，保证一致条件下的多次试验可能性不大[6]。借助声呐方程，通过接近实际参数的参数级建模，分析计算探测距离衰减率和压制扇面，是一种快速有效的分析评估干扰器干扰效果的方法，可为作战对抗策略提供一定的指导意义。

1 声呐工作背景模型

由经典声呐方程[7]可知，在没有干扰器的情况下，声呐工作时的环境噪声为各向同性背景噪声噪声级LN(dB)，其波束域的背景噪声级为LN-DI(DI为声呐的接收指向性指数)。

假设声干扰器相对声呐的方位为θ0，到达声呐接收机处的干扰级为LJ(dB)，声呐在只有干扰器存在时的方位谱图为P(φ)(φ∈Θ，Θ为声呐的观察视区)，则干扰器在观察方位θ(θ∈Θ)处的波束域大小为。因此，干扰器存在时声呐在观察方位θ处的波束域工作背景声压级LBI(θ)为[8]

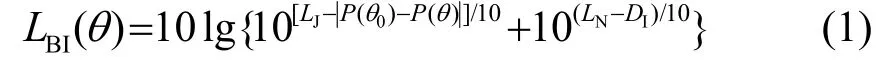
进一步地将P(φ)归一化，使最大值P(θ0)=0，则有P(θ)≤0，式(1)可简化为

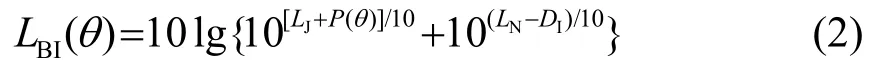
2 干扰器对声呐的干扰分析

分析干扰器对声呐的干扰效果，主要是分析、计算声呐的作用距离衰减率和干扰器对声呐的压制扇面。作用距离衰减率是指声呐由于干扰器的存在，其作用距离衰减的百分比。干扰器对声呐而言是有指向性的而不是各向同性的，因此作用距离衰减率是观察方位的函数。压制扇面是指干扰器对本舰的掩护范围，在该扇面内敌方声呐探测不到本舰。

2.1 对被动工作方式声呐的干扰分析

经典被动声呐方程为

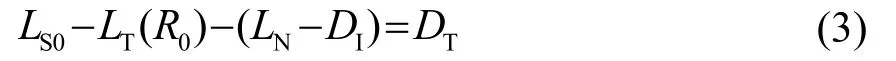
式中：R0是声呐的作用距离；LS0是辐射噪声源的声源级；LT(R0)是单程传播损失；LN是背景噪声级，DI是接收指向性指数，DT是接收检测域。各参数均以dB为单位。

(1) 作用距离衰减率

干扰器工作后，声呐的工作背景由LN-DI变为LB2(θ)。记声呐的作用距离由R0衰减为R(θ)，即满足：

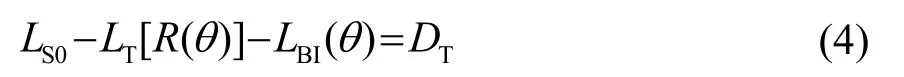
由式(3)和式(4)可知，声呐的单程传播损失减小了LBI(θ)-(LN-DI)，计算被动工作方式下声呐的作用距离衰减率为[R0-R(θ)]/R0×100%。

(2) 压制扇面

干扰器工作后，当干扰器成功掩护距离为r、辐射噪声级为LS的目标(我方舰艇)时，声呐方程应满足：

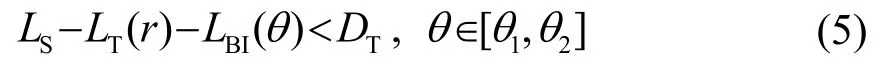
满足式(5)中的方位范围即为压制扇面范围[θ1,θ2]，压制扇面大小为θ2-θ1。

由式(3)和式(5)可得：

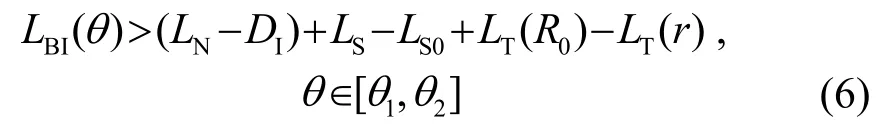
当LS-LS0+LT(R0)-LT(r)≤0时，在LJ+P(θ)＞0的情况下，式(6)对任意的θ∈Θ均成立。当SL-SL0+TL(R0)-TL(r)＞0时，将式(2)代入式(6)，整理可得：

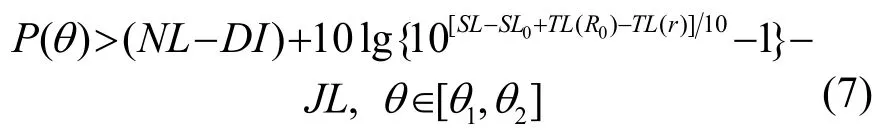
根据式(7)结合方位谱图P(φ)(φ∈Θ)，可给出干扰器对被动工作方式声呐的压制扇面范围[θ1,θ2]和压制扇面大小θ2-θ1。

(3) 建模参数

根据上述参数及建模及分析过程，总结分析干扰器对被动工作方式声呐的干扰效果需要的参数包括：接收阵阵型(阵列形式、阵元个数和阵元间距等)、工作频段、作用距离及论证参数(目标辐射源级、工作背景、工作频率、指向性指数等)、传播损失模型、干扰器对抗的典型态势、干扰器宽带干扰噪声强度和频率以及我方舰艇目标辐射噪声级。

2.2 对主动工作方式声呐的干扰分析

经典主动声呐方程为

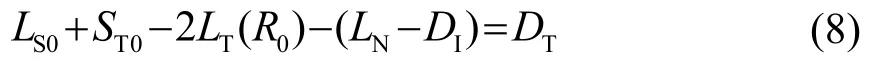
式中：R0是声呐的作用距离；LS0是发射声源级；ST0是目标强度；LT(R0)是单程传播损失；LN是背景噪声级；DI是接收指向性指数；DT是接收检测域。各参数均以dB为单位。

(1) 作用距离衰减率

干扰器工作后，由2.1节的分析可知，声呐的工作背景由LN-DI变为LBI(θ)。记声呐的作用距离由R0衰减为R(θ)，即满足：

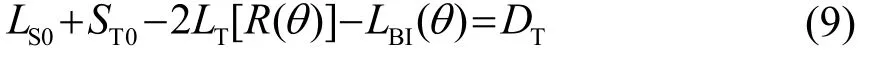
由式(8)和式(9)可知，声呐的双程传播损失减小了LBI(θ)-(LN-DI)，计算主动工作方式下声呐的作用距离衰减率为[R0-R(θ)]/R0×100%。

(2) 压制扇面

干扰器工作后，当干扰器成功掩护距离为r、目标强度为ST的目标(我方舰艇)时，声呐方程应满足：

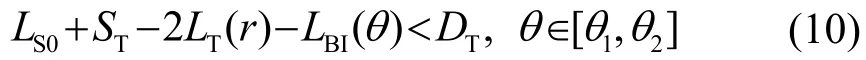
满足式(10)中的方位范围即为压制扇面范围[θ1,θ2]，压制扇面大小为θ2-θ1。

由式(9)和式(10)可得：

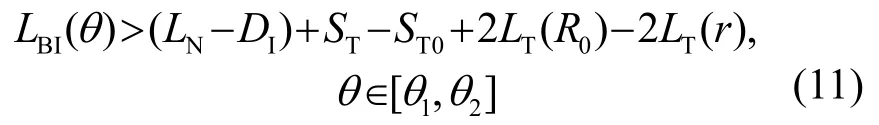
当ST-ST0+2LT(R0)-2LT(r)≤0时，在LJ+P(θ)＞0的情况下，式(11)对任意的θ∈Θ均成立。当ST-ST0+2LT(R0)-2LT(r)＞0时，将式(2)代入式(11)，整理可得：

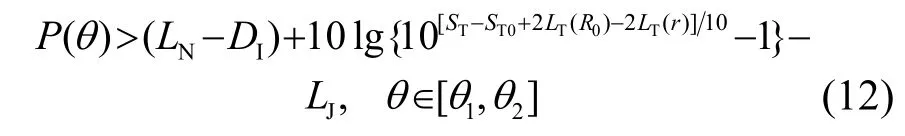
根据式(12)结合方位谱图P(φ)(φ∈Θ)，可给出干扰器对主动工作方式声呐的压制扇面范围[θ1,θ2]和压制扇面大小θ2-θ1。

(3) 建模参数

根据上述参数级建模及分析过程，可知干扰器对主动工作方式的干扰效果需要的参数包括：接收阵阵型(阵列形式、阵元个数和阵元间距等)、工作频段、作用距离及论证参数(发射源级、目标强度、工作背景、工作频率、指向性指数等)、传播损失模型、干扰器对抗的典型态势、干扰器瞄准干扰噪声强度和频率以及我方舰艇目标强度。

3 仿真分析

我方水下潜艇携带干扰器，敌方水面舰艇装备主被动声呐，潜艇被敌方声呐探测跟踪后适时释放干扰器，并在干扰器的掩护下迅速远离敌方舰艇，使其不能对我艇实施有效攻击。干扰器对主被动声呐的干扰效果仿真分析如下：

设某主被动声呐为均匀线列阵阵型，阵元个数为48，阵元间距为0.375 m，各向同性工作背景谱级为在频率1 kHz处为64 dB。被动方式工作频段为1～2 kHz，作用距离R0=22 km，主动方式工作频率为1.5 kHz单频，作用距离R0=31 km。设某一干扰器在均匀线阵的正横方位，在频率1～2 kHz内的干扰谱级为135 dB，瞄准频率干扰谱级为140 dB。假定干扰器和我方舰艇位于同一位置处，我方舰艇辐射噪声级与声呐论证辐射噪声级一致、我方舰艇目标强度与声呐论证目标强度一致。传播损失模型如图1所示。

(1) 干扰器距离声呐r=20、15、10 km时对声呐被动工作方式时的干扰效果。

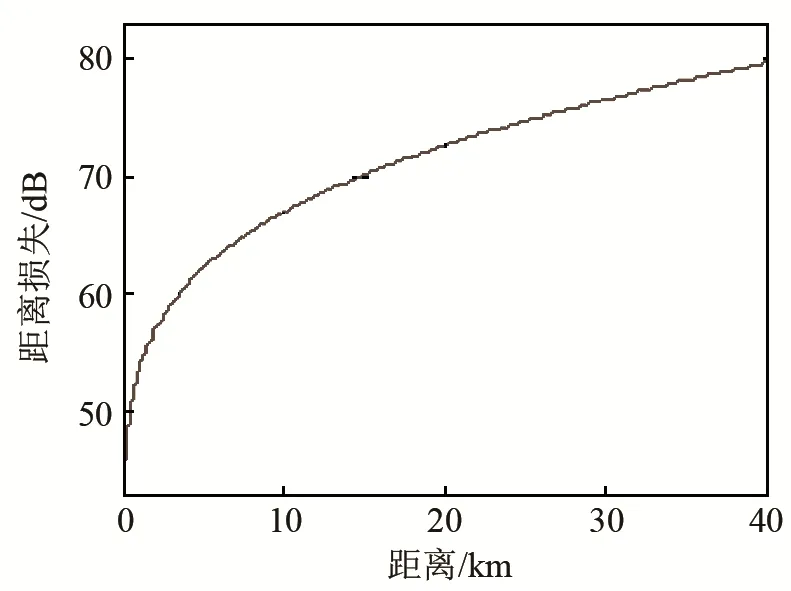
图1 传播损失模型Fig.1 The transmission loss model

根据声呐参数仿真干扰器存在时的方位谱图为P(φ)，计算指向性指数DI=15.6，工作频段1～2 kHz内背景噪声级LN=165 dB，到达声呐接收机处理频段内的干扰级LJ=165-LT(r)，由2.1节干扰分析可知干扰器存在时的声呐的单程传播损失LT[R(θ)]=LT(R0)-[LBI(θ)-(LN-DI)]，由传播损失模型可反推出R(θ)，计算作用距离衰减率为[R0-R(θ)]/R0×100%，结果如图2(a)所示；根据式(7)结合方位谱图P(φ)仿真分析压制扇面结果如图2(b)所示。统计在干扰方位处声呐被动工作方式作用距离衰减率分别为85.9%、90.9%、95.1%，干扰器对声呐被动工作方式的压制扇面分别为：15°、8.8°、6.2°。

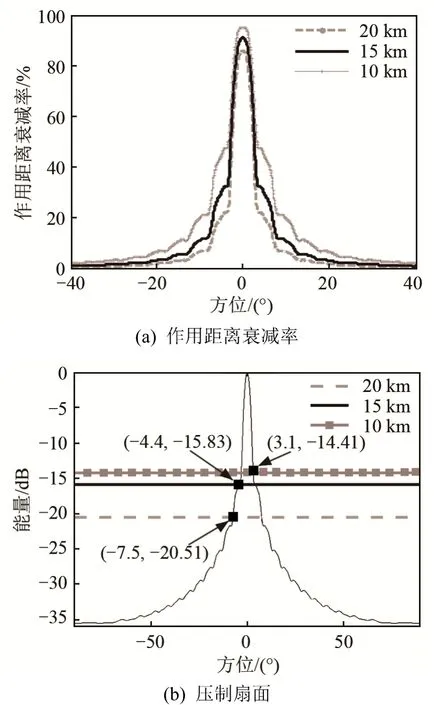
图2 干扰器对被动工作方式的干扰仿真Fig.2 The simulation of passive sonar under the interference of noise-jammer

(2) 干扰器距离声呐r=30、20、10 km时对声呐主动工作方式时的干扰效果。

根据声呐参数仿真干扰器存在时的方位谱图为P(φ)，计算指向性指数DI=15.6，工作频率处背景噪声谱级LN=140 dB，到达声呐接收机处的干扰谱级LJ=140dB-LT(r)，由2.2节干扰分析可知，干扰器存在时的声呐的双程传播损失2LT[R(θ)]=2LT(R0)-[LBI(θ)-(LN-DI)]，由传播损失模型可反推出R(θ)，计算作用距离衰减率为[R0-R(θ)]/R0×100%，如图3(a)所示；根据式(12)结合方位谱图P(φ)仿真分析压制扇面结果如图3(b)所示。经统计可得，干扰方位处声呐主动工作方式时的作用距离衰减率分别为65.0%、73.1%、82.3%，干扰器对声呐主动工作方式的压制扇面分别为42.8°、10.2°、4.4°。

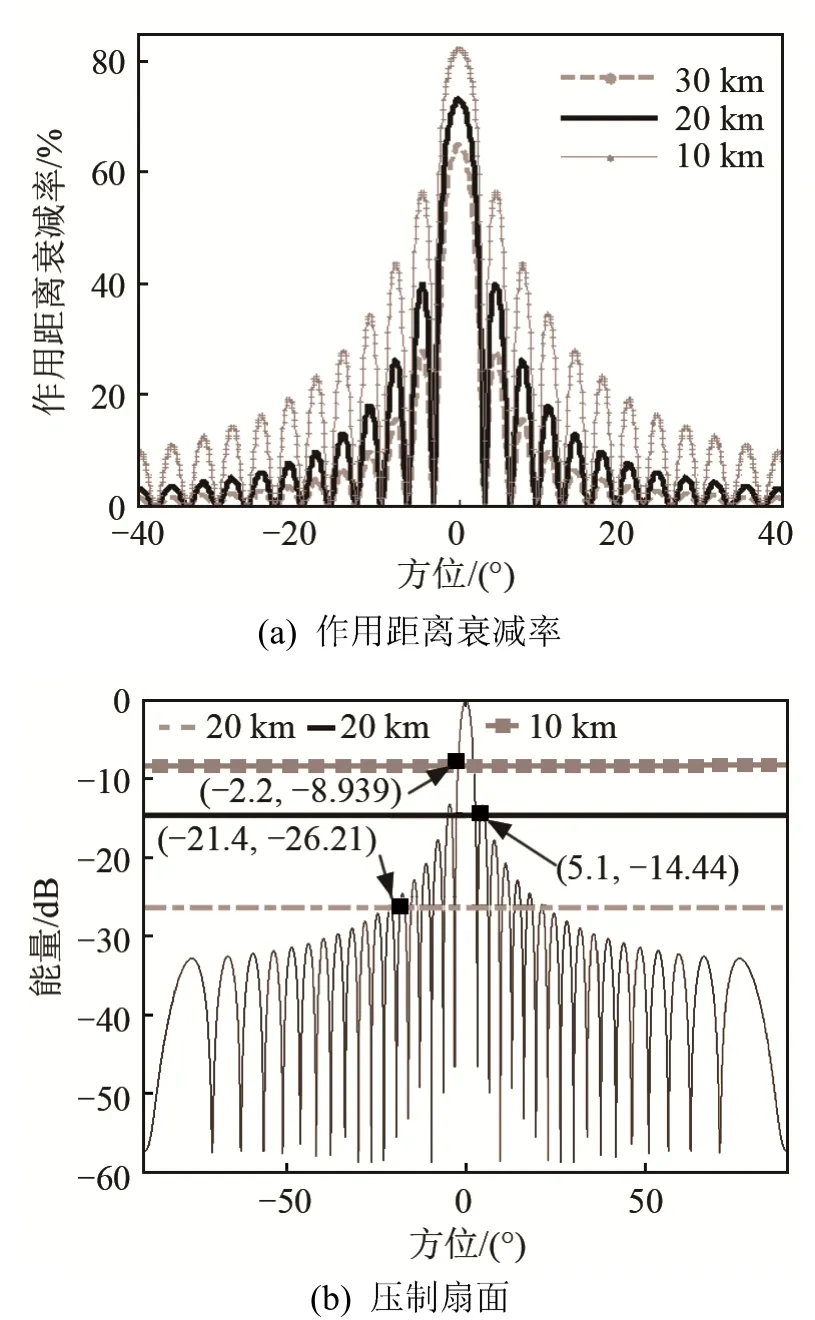
图3 干扰器对主动工作方式的干扰仿真Fig.3 The simulation of active sonar under the interference of noise-jammer

4 结 论

本文在干扰器存在时声呐工作背景模型的基础上，针对声呐的主、被动工作方式分别建立了干扰器干扰效果参数级模型，并分析给出了探测距离衰减率和压制扇面的计算。最后通过仿真实例给出了干扰器对主、被动声呐的干扰效果分析。本文提出了的参数级模型分析方法是一种快速有效的衡量干扰器干扰效果的方法，可为作战时对抗策略提供一定的指导意义。