一种基于MSR的中等斜视多子阵合成孔径声呐距离多普勒算法

吕金华，唐劲松，吴浩然

(1.武汉船舶职业技术学院电气与电子工程学院，湖北武汉430050；2.海军工程大学电子工程学院，湖北武汉430033)

0 引 言

虽然合成孔径声呐(Synthetic Aperture Sonar,SAS)技术起源于合成孔径雷达(Synthetic Aperture Radar, SAR)技术，但是水中声速的低速性导致SAS表现出两个特点：(1) SAS在收发期间的横向走动量不可忽略，从而使得在SAR中常用的“停走停”假设[1-2]不适用于SAS，必须使用更复杂的“非停走停”假设[3-4]。(2) 为了提高速度和测绘速率，实用SAS系统都使用单发射多接收技术，简称多子阵SAS。SAS的这两个特点将造成中等斜视多子阵成像算法相比小斜视或正侧视多子阵SAS成像算法有两点不同：

(1) 需要考虑“非停走停”假设的孔径依赖性。多子阵SAS“非停走停”的工作模式，导致其精确距离史非常复杂，很难直接用于成像算法，需要进行近似处理。目前，针对该问题，最常用的方法是忽略“非停走停”的孔径依赖性，用波束中心线上的时延代替波束内所有目标在一个脉冲内的横向走动量，进而计算出每个子阵的近似距离史[5-6]。但是，该方法仅仅能够在小斜视情况中使用，当斜视增大时，忽略“非停走停”的孔径依赖性将导致较大的相位误差，从而影响成像效果。

(2) 需要考虑阵元依赖性。多子阵SAS成像算法最常用的方法是忽略回波信号的阵元依赖性，通过时域重排的方式将多子阵SAS信号重构成单阵信号后，再使用已有的常规逐线成像算法，如距离多普勒算法 (Range Doppler Algorithm, RDA)[7]、线性调频变标算法(Chirp Scaling Algorithm, CSA)[8-10]、omega-KA[11]等。但是，在中等斜视时，回波信号的阵元依赖性将增大，如果将其忽略，可能导致成像结果出现散焦。

为此，本文提出了一种基于MSR的中等斜视多子阵RDA。该算法在波束中心处用四阶方位时间的泰勒级数近似精确距离史，得到近似距离史，再用MSR[12]求解近似距离史对应的窄带回波信号的二维谱解析解。由于精确距离史包含了“非停走停”的影响，而泰勒级数展开考虑到了四阶方向时间，因此本文提出的算法没有忽略“非停走停”假设的孔径依赖性，解决了传统算法忽略了“非停走停”假设孔径依赖的问题。

为了解决阵元依赖的问题，先对每个子阵信号进行方位谱扩展，增加单个子阵方位向信号处理的点数；再对每个子阵信号使用基于MSR的RDA进行成像处理，得到每个子阵欠采样的成像结果；通过将每个子阵的成像结果进行叠加的方式，消除欠采样的影响，得到最终的成像结果。最后，通过仿真实验证明了本文算法的有效性和正确性。

1 斜视多子阵SAS模型

1.1 精确距离史

如图1所示，有一个直角坐标系Oxyz，其中x轴与声呐的前进方向平行，y轴在水平面内与x轴垂直，z轴的正方向垂直向下。假设t是慢变时间，v是声呐的速度，r是发射阵与目标在波束中心穿越时刻的斜距，θsq是发射阵在波束中心穿越时刻的斜视角，θsqi是子阵i在波束中心穿越时刻的斜视角，θba是声基阵的偏航角，θbe是声基阵的下视角，di表示第i个接收阵与发射阵之间的基线长度，点目标P的坐标是(rsinθsq,rcosθsq,-rcosθba)，RT(t;r)是发射阵与目标的瞬时斜距，RRi(t;r)是子阵i与目标的瞬时斜距。斜视SAS的几何模型如图1所示，图中表示收发共用阵，表示接收子阵，表示第i子阵在收发期间的延时时间。

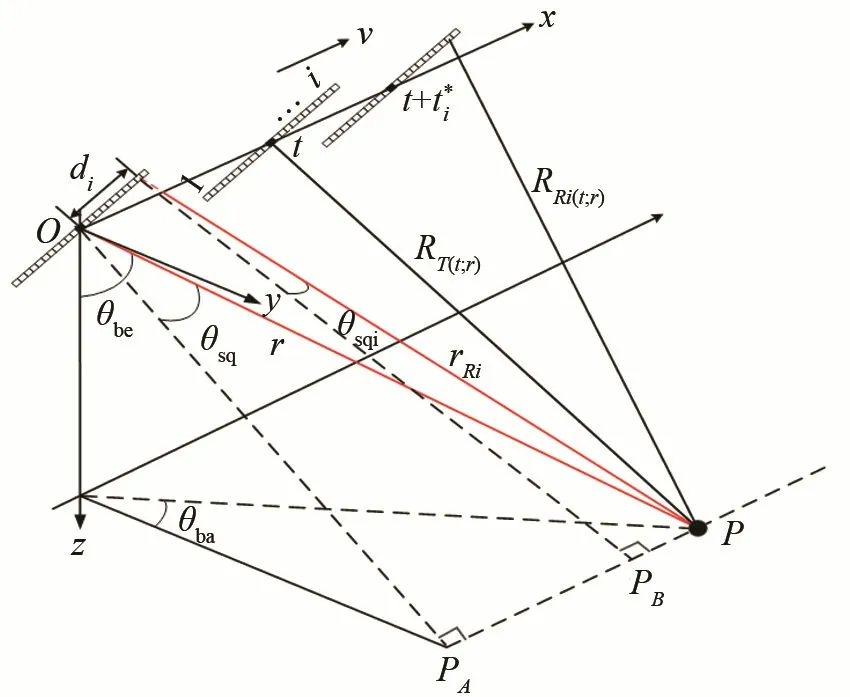
图1 斜视SAS几何模型.Fig.1 The geometry model of squint SAS

根据图1的几何关系，得到P的精确距离史为

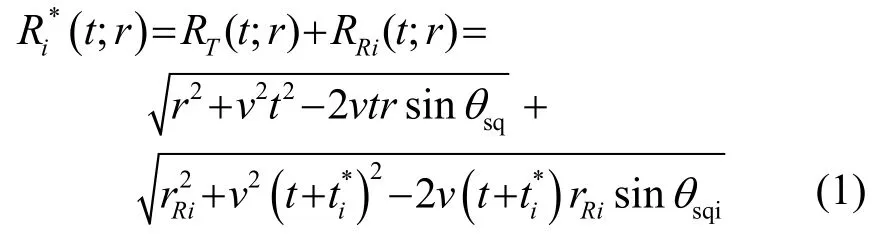
根据式(1)和式(2)，解得精确距离史为

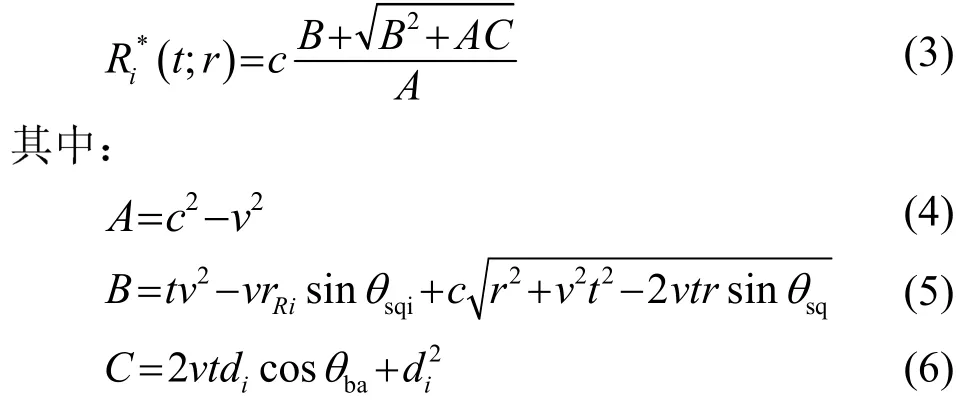
在波束中心处用四阶泰勒级数对精确距离史展开，得到近似距离史为

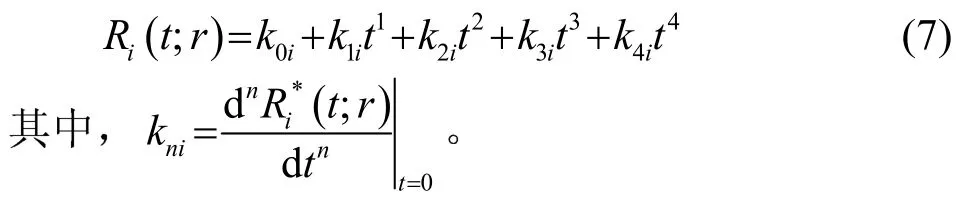
1.2 点目标回波信号模型

假设τ是快变时间，p(⋅)是发射信号包络，ωa(⋅)是发射阵与单个接收阵元的合成波束指向性函数，k是调频斜率，c是声速，f0是载频，那么第i个接收子阵的回波信号解调至基带后，其表达式为

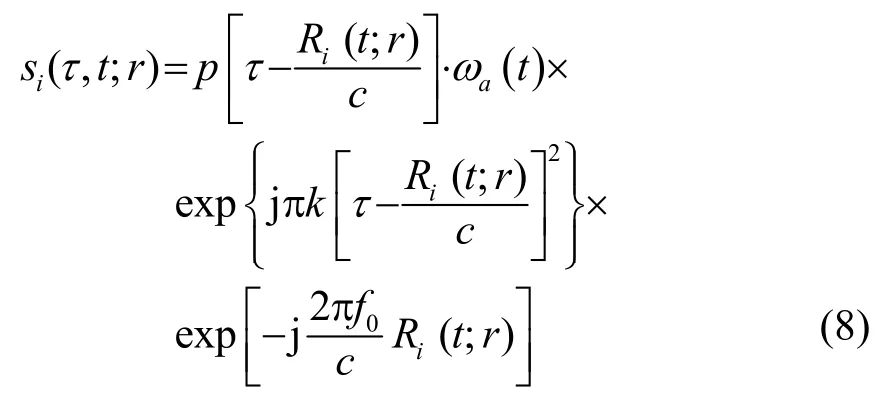
2 算法推导

2.1 点目标二维谱解析解

为了得到式(8)所示信号的二维谱解析解，借用MSR[13]，可直接给出单个子阵点目标二维谱的解析解为

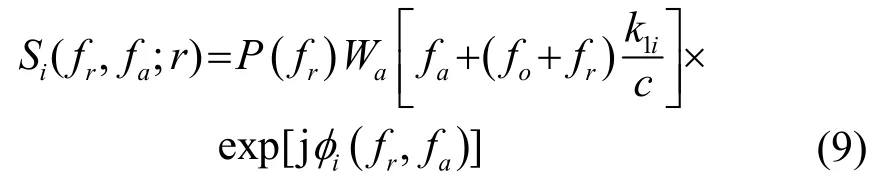
其中：P(⋅)发射脉冲信号谱的包络；fr表示距离频率；Wa(⋅)表示方位频谱的包络；fa表示多普勒频率；φi(fr,fa)表示SSi(fr,fa;r)的相位。将φi(fr,fa)对fr进行幂级数展开，保留至四阶项，得到：

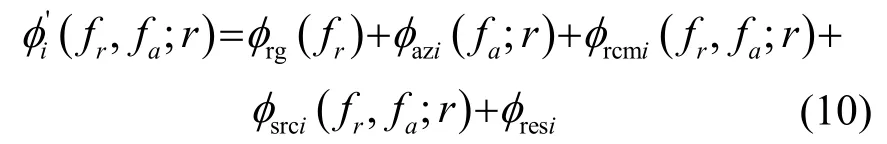
其中：φrg(fr)表示脉冲压缩项；φazi(fa;r)表示方位调制项；φrcmi(fr,fa;r)表示线性相位项；φsrci(fr,fa;r)表示距离和方位耦合项，是二次距离压缩(Secondary Range Compression, SRC)的来源缩项；φresi表示剩余相位项。其表达式分别为

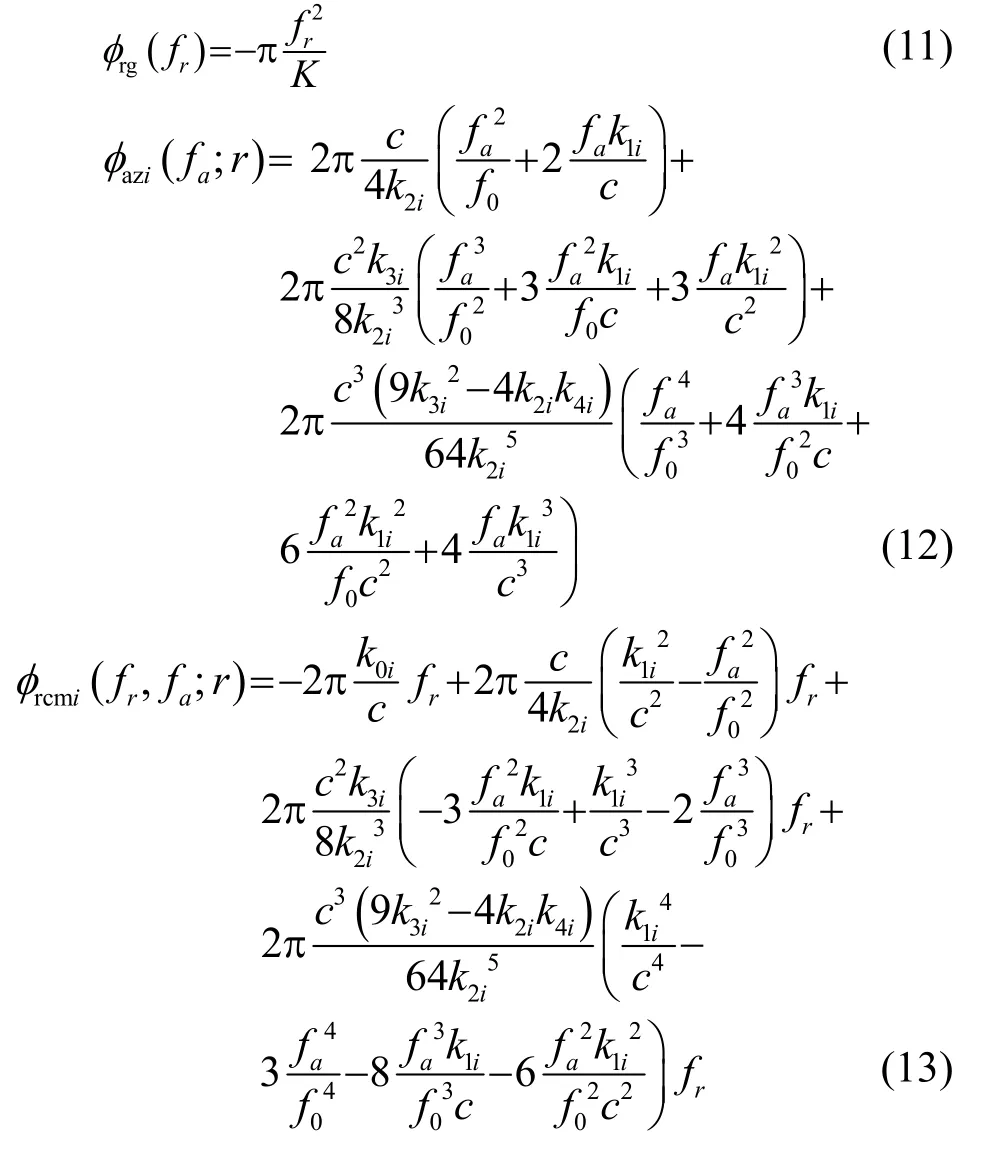
2.2 算法实现过程

结合式(9)中的二维谱解析解和经典RDA原理，中等斜视多子阵RDA的实现过程，如图2所示，具体实现步骤如下：

(1) 进行多普勒中心频率搬移。在斜视的情况下，信号的能量在方位频域可能发生“卷绕”[12]，多普勒中心频率fdc表达式为

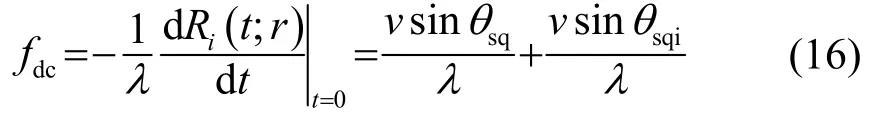
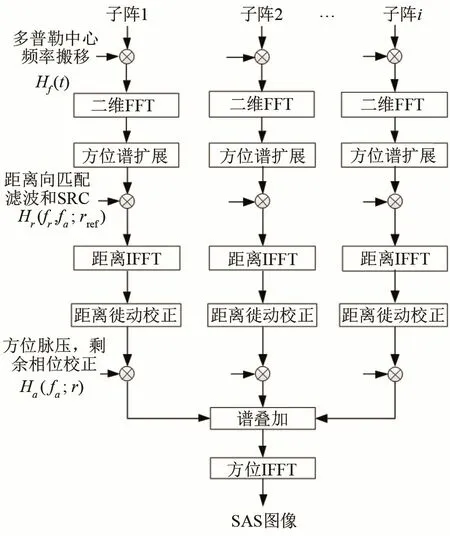
图2 斜视SAS距离多普勒算法流程Fig.2 Flow chart of RDA for squint SAS

其中：λ是波长，由于r远远大于di，因此θsqi可以近似为θsq，进而。为了解决方位频域“卷绕”的问题，在方位时域通过线性相位相乘的方式，将方位谱的中心由0多普勒频率搬移至fdc多普勒中心频率，从而解决方位频域能量“卷绕”的问题。其中相位相乘的因子可表示为

在进行多普勒中心频率搬移后，多普勒频率的变化范围为

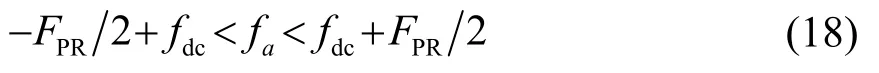
其中，FPR表示脉冲重复频率。

(2) 进行方位向快速傅里叶变换(Fast Fourier Transform, FFT)和距离向FFT。执行该步骤后，每个子阵信号的解析表达如式(9)所示，其中多普勒频率范围如式(18)所示。

(3) 进行方位谱扩展。每个接收阵接收到的数据是方位时域信号的降采样数据。为了满足对单个子阵信号处理长度的要求，用图3所示的方法将方位谱的长度增加N倍，即将方位谱信号复制N份，再进行排列。在图3中，M为一个合成孔径长度内的脉冲数，N为接收阵的个数。

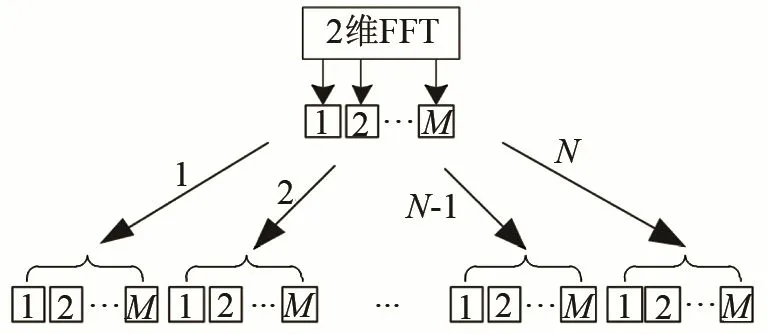
图3 方位谱扩展Fig.3 Azimuth spectrum expansion

(4) 进行距离向匹配滤波和SRC。根据式(11)可以得到距离向匹配滤波的相位相乘因子。由于SRC项对距离的依赖较弱，其相位φsrci(fr,fa;r)可以用参考距离rref处的相位代替[12]。因此，通过一个相位相乘可同时完成距离向匹配滤波和SRC，该相位相乘的因子为

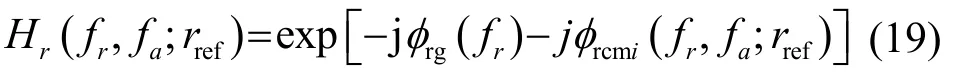
得到二维频域信号为

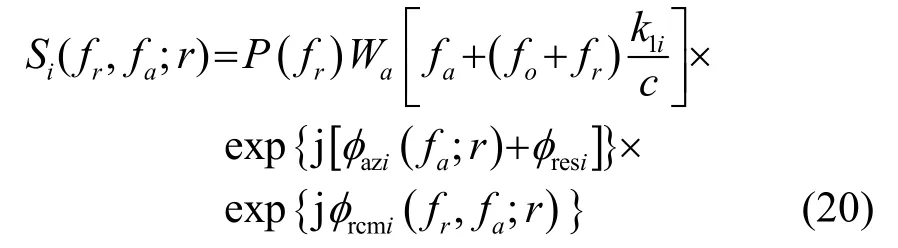
(5) 通过距离向快速傅里叶逆变化(Inverse Fast Fourier Transform, IFFT)，得到距离多普勒域信号

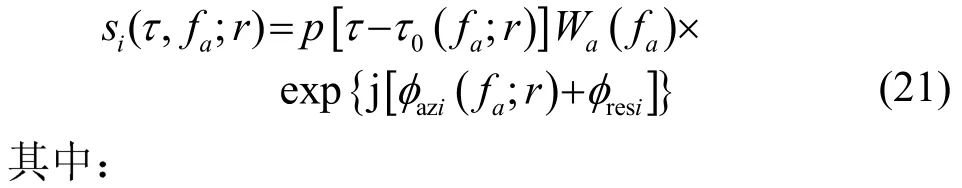
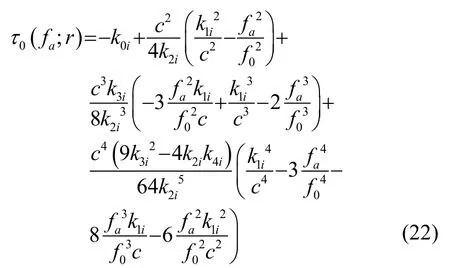
(6) 通过插值的方式进行距离徙动校正(Range Cell Migration Correction, RCMC)，消除距离方位耦合。由式(21)可知，需要校正的距离徙动量为

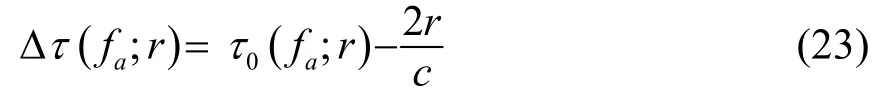
得到RCMC后的距离多普勒域信号为

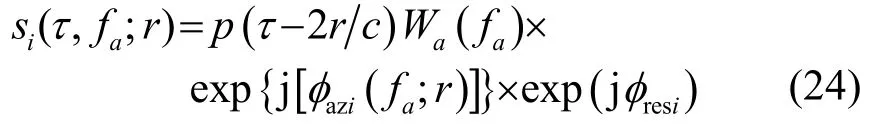
(7) 进行方位向匹配滤波和剩余相位校正。方位向匹配滤波器是式(24)中第一个指数项的复共轭，由相位相乘实现。剩余相位φresi独立于距离频率和方位频率，因此对目标的聚焦没有影响，但是会导致目标强度随距离变化，可以通过相位相乘的方式进行补偿。因此，通过一个相位相乘可同时完成方位向匹配滤波和剩余相位校正，该相位相乘的因子为

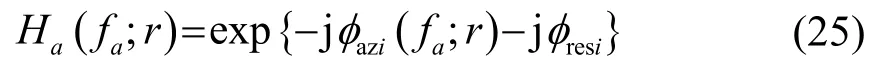
(8) 将每个子阵的信号进行相干叠加，消除单个子阵欠采样带来的混叠现象。

(9) 进行方位逆傅里叶变换，得到二维时域信号，即成像结果。

3 仿真实验

为验证本文算法的有效性，进行了仿真实验。

3.1 仿真参数

假设每个子阵接收信号的距离史由式(3)给出；场景为理想平地，5个理想点目标的沿x轴方向的方位向和距离向都间隔3 m；信号载频为150 kHz、信号带宽为20 kHz、信号脉宽20 ms、脉冲重复时间0.40 s、接收阵宽度为0.04 m、发射阵宽度为0.08 m、接收阵数量为25、声呐速度为1.25 m·s-1、斜视为2°、6°和10°。

3.2 仿真结果

用本文和文献[14]提出的基于置相位中心天线(Displace Phase Centre Antenna, DPCA）的RDA分别对场景的回波信号进行成像处理，得到的成像结果如图4所示。

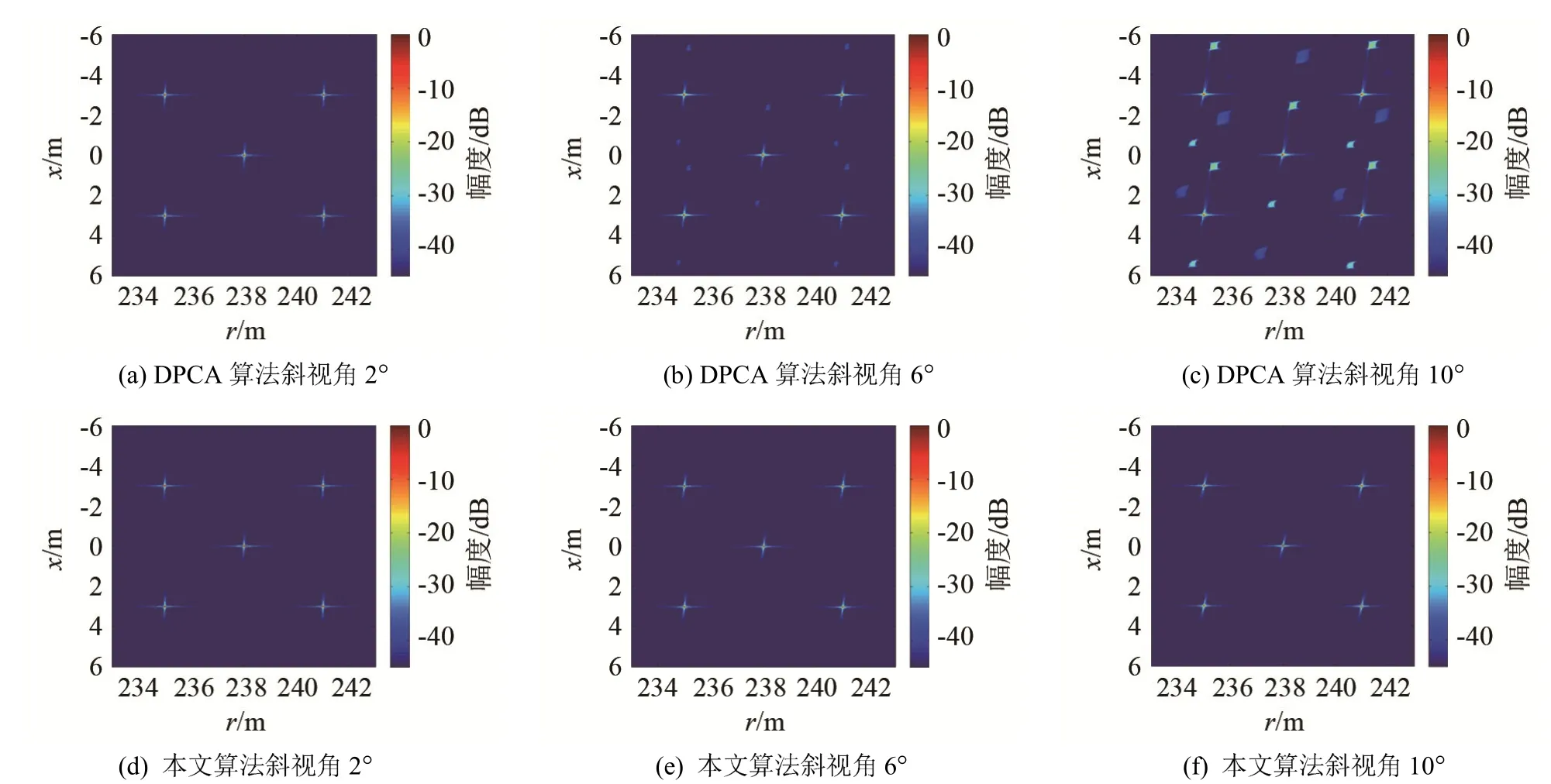
图4 基于DPCA的距离-多普勒算法与本文算法的仿真成像结果Fig.4 Simulation imaging results of DPCA based RDA and the algorithm in this paper

从图4中的结果可见，斜视角较小时，DPCA方法能够获得很好的成像结果，但是随着斜视角的增大，DPCA的成像结果越来越差，虚假目标的能量越来高。而本文方法的成像结果基本上不受斜视角的影响，在每种斜视角下都取得了很好的成像结果。为了能够更加清楚地比较两种方法的成像效果，取图4中的中心点目标的方位向和距离剖面，并对其方位和距离向的分辨率、主副瓣比(Peak Sidelobe Ratio, PSLR)和积分旁瓣比(Integrated Sidelobe Ratio, ISLR)进行测量，结果如表1所示。在不同斜视角下，两种方法点目标的方位剖面结果如图5所示。

当斜视角为2°时，从图5和表1的结果可知，两种方法的成像结果基本一致。当斜视角增大至6°和10°时，在图5中DPCA方法虚假目标的幅度明显高于本文的方法，同时随着斜视角的增大而增大，而本文方法的虚假目标幅度依然与2°斜视角的成像结果一致。从表1还可以看出，DPCA方法的方位向分辨率、距离向PSLR、方位向PSLR和距离向ISLR随着斜视角的增大而出现明显变差，而本文方法的成像结果随斜视角的变化很小。

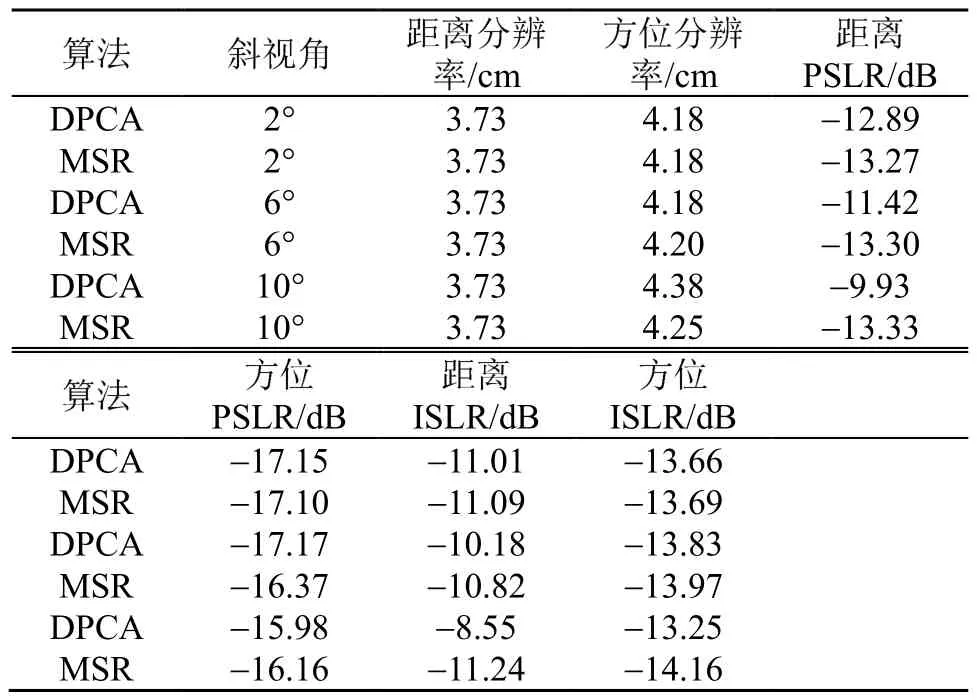
表1 两种算法的图像参数测量结果Table 1 Image parameter measurement results of the two algorithms

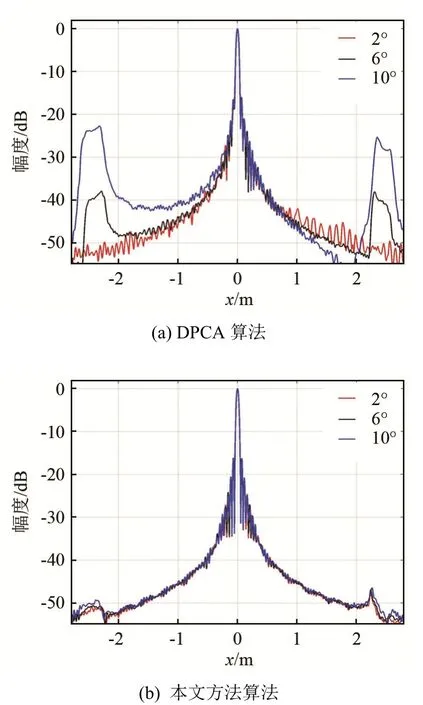
图5 不同斜视角的方位响应剖面Fig.5 The azimuth response profiles at different squint angles

4 结 论

本文提出了一种基于MSR的中等斜视的多子阵RDA，解决了中等斜视时“非停走停”假设的孔径依赖性和阵元依赖性不能被忽略的问题。

通过与现有斜视多子阵RDA进行仿真对比试验，得出以下结论：

斜视角为2°时，基于DPCA的算法和本文提出的多子阵RDA算法的成像质量一致，当斜视角增加到6°和10°时，本文算法的成像效果明显好于DPCA算法。

在中等斜视时，本文算法相比DPCA算法有更好的成像结果，但是由于本文算法需要对每个子阵单独成像，因此存在运算效率偏低的问题。