基于压电测力仪的模拟加载标定方法研究
2020-07-07王新蕾任宗金
张 军,王新蕾,任宗金
大连理工大学 机械工程学院,辽宁 大连 116024)
0 引言
在高端装备制造和航空航天矢量力测量领域,测试装置被广泛应用于矢量力的精确测量[1]。对测力仪进行合理的标定是对力值的精确测量的前提,这对直接影响矢量力测试装置测试性能的标定精度提出了要求。
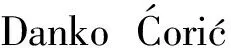
压电石英具有高刚度、高固有频率和优良的静态特性等优点,适用于大力值比矢量力测量[6]。因此,本文以正方形四点布置的压电测力仪为研究对象,针对大力值比测力仪标定中侧向合力波动问题,提出了一种旋转模拟加载的标定方法。
1 模拟加载法结构
基于文献[7],本文设计了模拟加载标定装置对测力仪进行大力值比模拟加载。模拟加载装置可以产生偏离主向z轴2°的大力值比矢量力,实现推力矢量的模拟加载,原理如图1所示。模拟加载装置可以通过8个均匀分布的螺纹孔绕z轴旋转,实现在同一圆周上8个工位的大力值比矢量力加载。
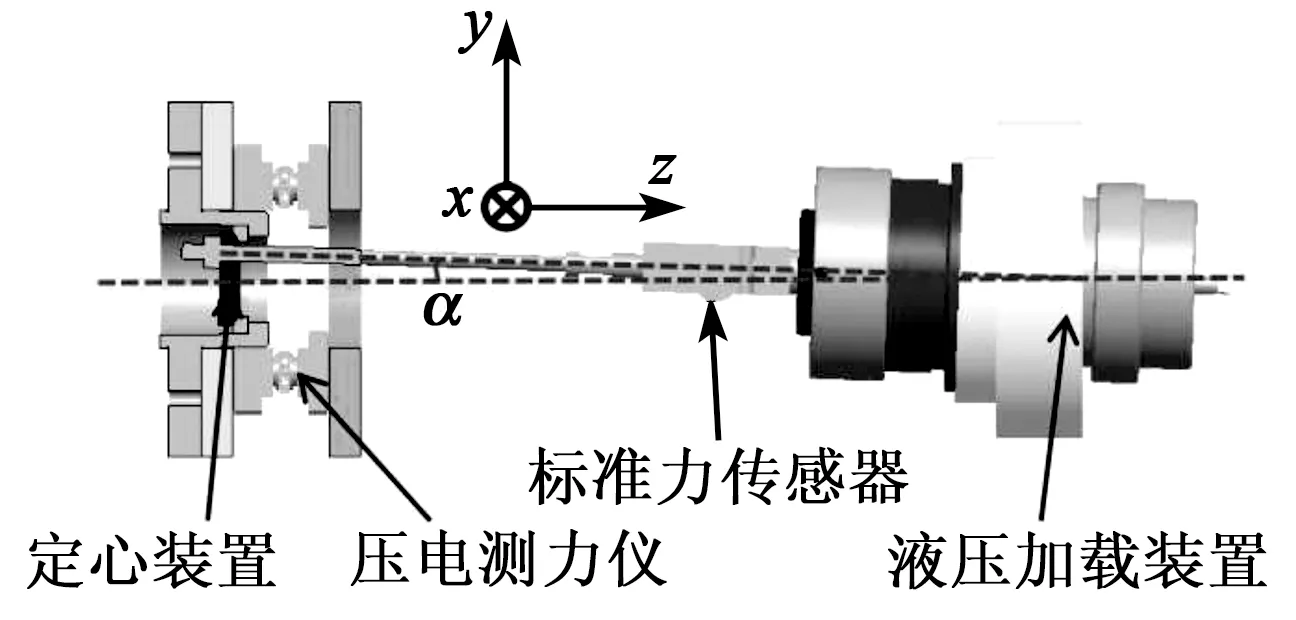
图1 模拟加载标定结构示意图
本装置中所使用的四点布置式压电测力仪已经过三向正交标定,其x、y、z向非线性误差、重复性误差均低于0.50%,向间干扰均低于2%。
2 模拟加载误差模型
该模拟加载标定系统主要由加载装置和作为测量装置压电测力仪组成。在模拟加载的过程中,加载装置和测量装置协同作用,因此,在模拟加载测量的过程中不仅包含测试系统本身的测量固有误差,还包括模拟加载过程中加载误差。
设Fxe1、Fye1为x、y向力的测量固有误差,Fze2、Fye2为x、y向力的加载标定误差,故在模拟加载的标定实验中,测试系统x、y向输出力值总误差Fxe、Fye分别为
Fxe=Fxe1+Fxe2
(1)
Fye=Fye1+Fye2
(2)
设Fxye1为侧向合力的测量固有误差,Fxye2为侧向合力加载标定误差,测试系统侧向输出合力值总误差Fxye为
Fxye=Fxye1+Fxye2
(3)
大力值比矢量力侧向合力的测量直接影响力值角度的测量精度。为了得到侧向合力中测量系统固有误差,必须分离加载过程中的标定误差。
模拟加载实验过程中,加载点相对于测力仪绝对位置不变,加载装置机械结构的加工、装配误差均可简化为加载装置轴线与测力仪轴线间的相对位置误差。
加载装置与测力仪定心装置间的相对位置模型如图2所示。图中,P为加载装置的作用点,OA为测力仪轴线;O′A′为加载装置轴线,α、α′分别为理想加载角度与实际加载角度;β为加载方位角,是加载点与测力仪y轴正向所成的角度,在八工位旋转加载时呈45°阶梯增长;λ为加载装置轴线与x轴正向所成的角度。
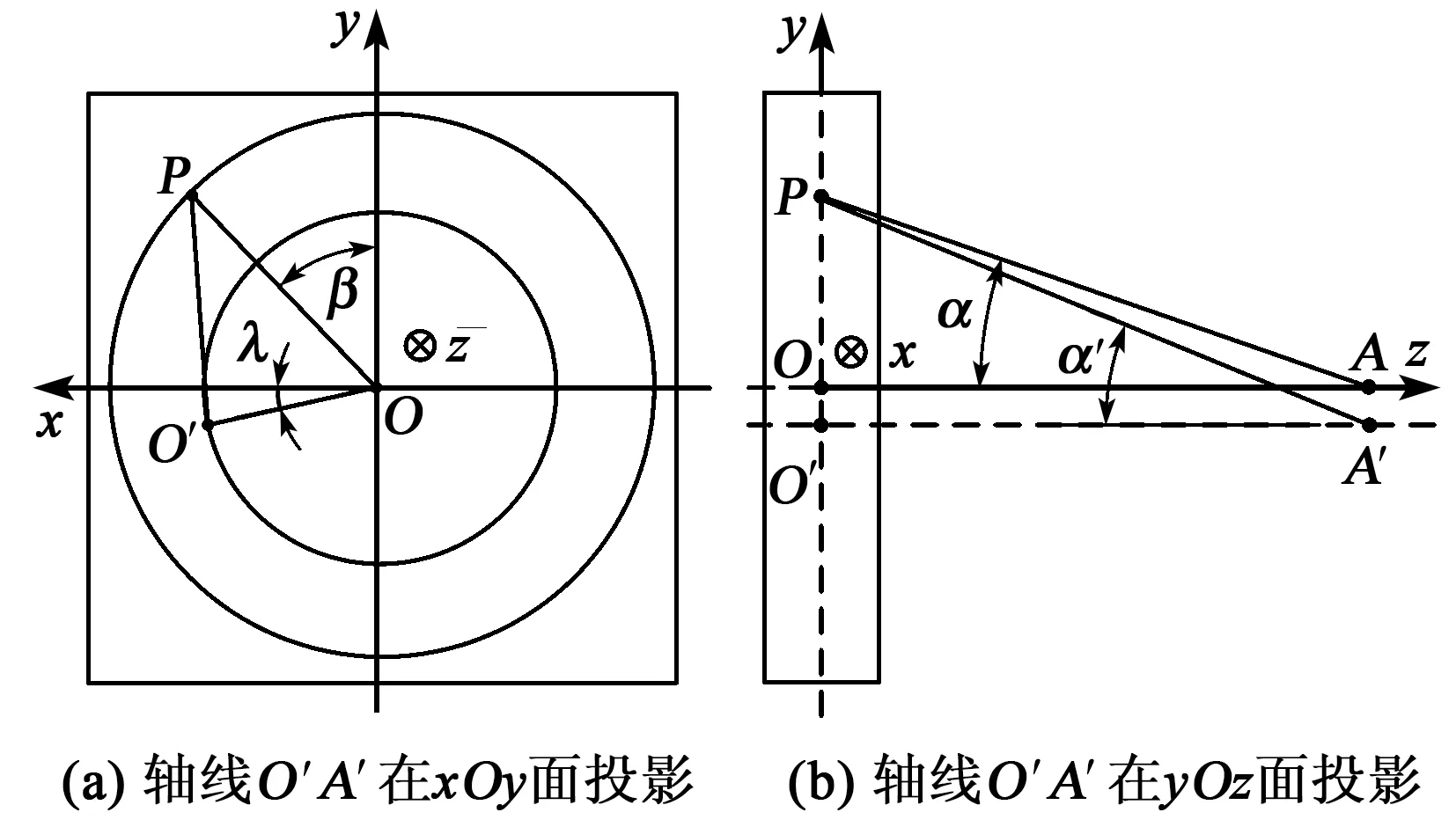
图2 模拟加载轴线偏移模型理论分析图
由图2可知,加载装置轴线O′A′与测力仪轴线OA的同轴度误差,导致加载装置产生的加载力的实际作用方向与理想加载方向产生偏差,从而使得加载力值在侧向方向上的分力产生较大变化。
基于力的分解原理,理想状态下施加在测力仪上的侧向合力值Fxy为
(4)
存在轴线偏移时,侧向合力的实际值Fxy为
(5)
由式(5)可知,在加载力值不变的情况下,测力仪侧向输出合力F′xy与PA′和β相关。在大量程比测力仪标定过程中,OA与O′A′间差距较小,因此,F′xy输出值主要受β的影响,且随β的变化呈周期性变化。取PA′=460 mm、OP=17.2 mm、OO′=2 mm、λ=30°,F分别取1 500 N、3 000 N、4 500 N、6 000 N、7 500 N,Fxy的理论波动曲线如图3所示。

图3 侧向合力随β变化波动图
由图3可见,加载装置轴线偏移引起侧向合力Fxy随推力偏移方位角β的变化,理论上其波动趋势符合确定的函数规律,其周期为360°,且随着加载力值的增加,其波动幅度也在增加。
3 旋转模拟加载法标定实验
基于以上理论误差分析模型,提出旋转模拟加载标定法。实验时,将模拟加载装置、定心装置、标准力传感器、连杆整体同步旋转,杜绝各部分间发生相对运动,保证加载装置轴线与测力仪轴线的相对位置不发生变动,使得加载误差中的系统误差随标定工位的旋转规律性展现。为了验证旋转模拟加载法的可靠性,通过两种标定实验方法对测力仪进行模拟加载,一种为旋转模拟加载标定法;一种为非旋转模拟加载标定法,在标定过程中,不限定模拟加载装置、定心装置、标准力传感器、连杆间的相对位置。采用图4所示的标定系统,按照两种方法通过模拟加载标定装置对测力仪的8个工位施加0~7 500 N的阶梯加载,记录测力仪输出,如表1~6所示。
图4 模拟加载标定系统图
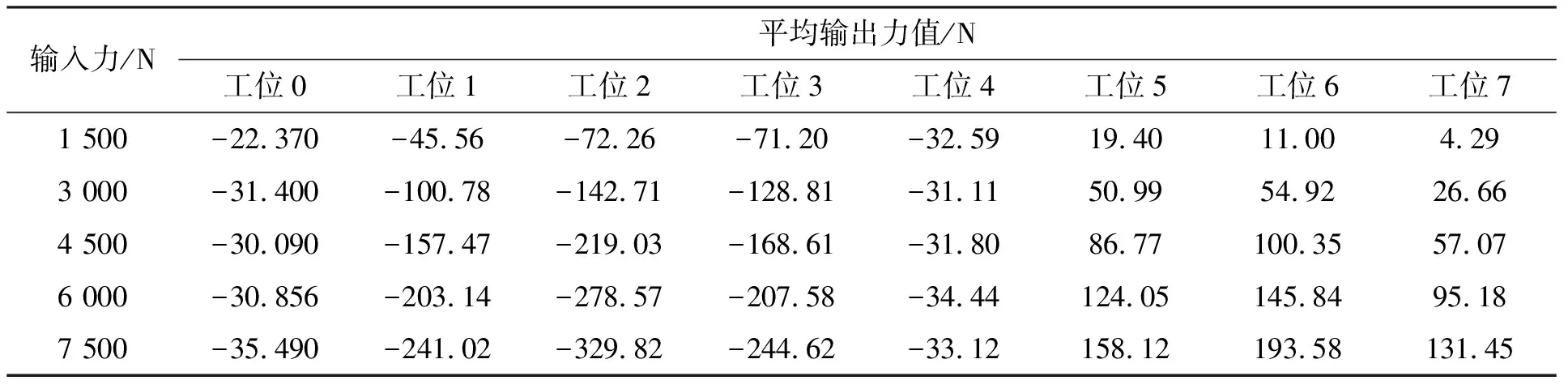
表1 非旋转标定法x向标定数据值
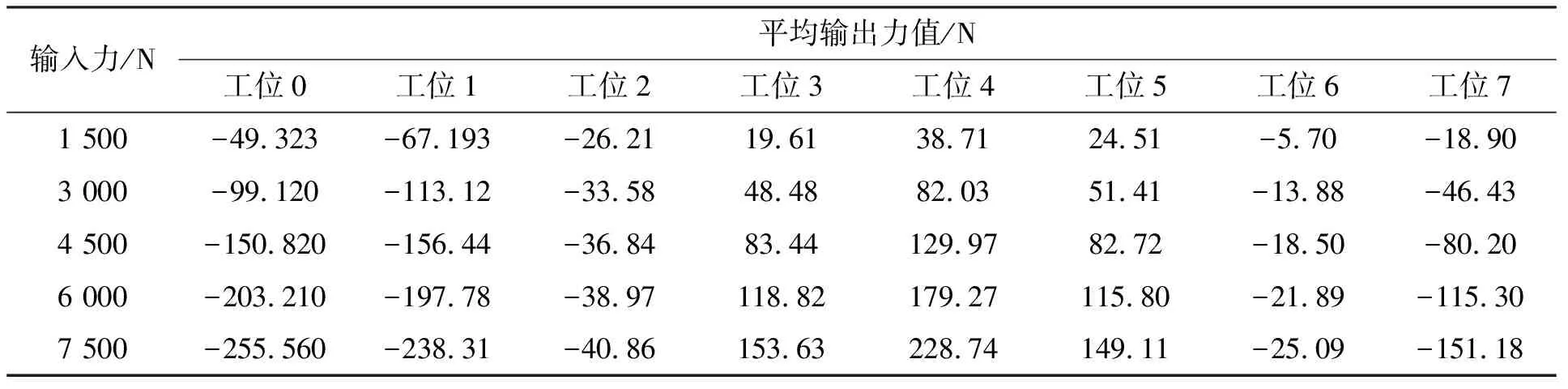
表2 非旋转标定法y向标定数据值

表3 非旋转标定法z向标定数据值

表4 旋转标定法x向标定数据值

表5 旋转标定法y向标定数据值
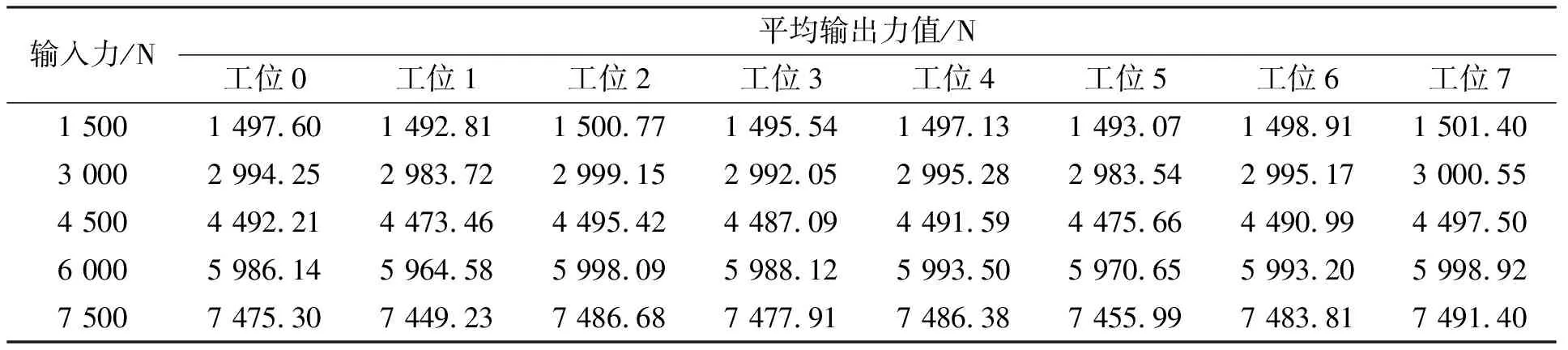
表6 旋转标定法z向标定数据值
由表1~6可知,在两种方法的旋转模拟加载的实验中,测力仪三向合力输出的最大误差均低于0.50%,符合测力仪的性能要求。图5、6分别为两种模拟加载法的侧向合力输出的波动曲线。
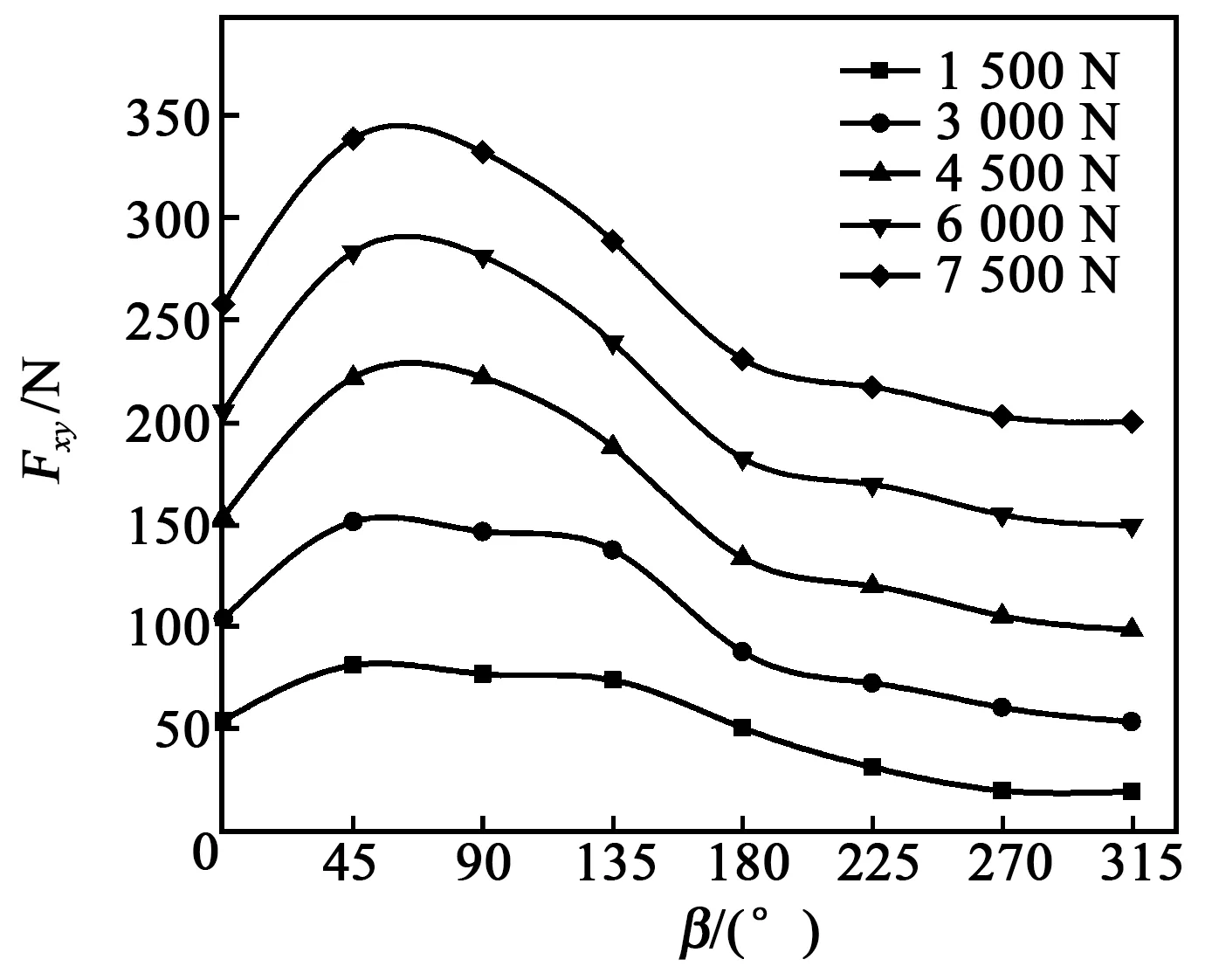
图5 非旋转模拟加载标定法侧向合力值输出曲线
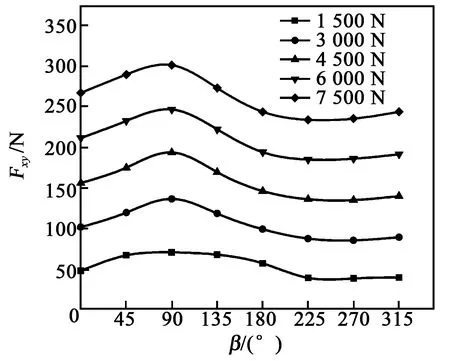
图6 旋转模拟加载标定法侧向合力值输出曲线
由图5、6可见,采用旋转模拟加载标定法时,测力仪侧向合力输出值的波动幅度远低于采用传统模拟加载标定法时的波动幅度;旋转模拟加载标定法侧向合力输出曲线的形状、波动幅度均与理论波动曲线十分相似,验证了所提误差理论模型与旋转模拟加载标定法的合理性。
图7为不同力值下两种标定方法侧向合力输出误差对比图。

图7 不同力值下两种标定方法侧向合力误差对比图
由图7可见,随着加载力值的增大,两种标定方法的误差均在降低,但旋转模拟加载标定法侧向合力输出误差始终低于非旋转模拟加载标定法,在7 500 N情况下误差最大降低了18.7%F.S.。
综上对比两种标定方法的侧向合力输出曲线及侧向合力输出误差,证明了旋转模拟加载标定法的合理性。
4 结束语
本文以大力值比载荷标定装置的加载误差为研究对象,针对同一力值模拟加载工况下,其侧向输出误差较大且变化不规律的问题,分析了标定误差和测量误差的影响因素。基于测试系统力加载模型,考虑模拟加载装置轴线与测力仪轴线位置偏差,探求轴线偏差对侧向合力干扰机理,得到了因力源传输路径的几何偏移和偏转产生的接触力是误差过大的主要原因。建立了同轴度误差对于加载装置所产生侧向合力影响的数学模型,得到了偏斜加载的侧向合力输出的理论几何变化曲线。针对力值曲线的特点,基于误差规律表现的思想,提出旋转加载标定法。对测试系统应用两种模拟加载标定法进行实验,发现旋转加载标定法的侧向合力输出曲线波动与理论曲线更接近,且其输出规律性表现明显。旋转加载标定法侧向合力输出误差相对于非旋转模拟加载标定法最大降低了18.7%F.S.,表明了所提旋转模拟加载标定方法的有效性和合理性,为提高测力仪的标定精度提供了一种新思路。
