基于压电陶瓷神经网络模型的模型抑振研究

姚 壮，周孟德，温正权，唐琳琳，王琴琴，刘 巍

大连理工大学 机械工程学院，辽宁 大连 116024)

0 引言

风洞试验对于飞行器的研制开发与性能检测有着重要影响，其有助于降低飞行器研制的风险和成本[1]。在风洞模型支撑方式中，尾撑方式以结构简单、对流场干扰小等优点最常用，但由模型、测力天平、尾撑支杆、弯刀组成的系统构成了典型的悬臂结构，致使系统刚度低、阻尼小，易与宽频气动载荷产生耦合，从而引起风洞试验中模型产生低频、大幅值振动[2]，这将导致测力天平数据测量不准确，风洞试验无法顺利进行。因此，针对风洞支杆模型进行振动抑制，对于风洞试验的顺利进行与数据的精确性有重大意义，是风洞试验领域的重要课题。

抑振器需在小尺寸下具备高输出性能及高频响应特性，多采用压电陶瓷作动器。控制方面，主动式抑振以效果好、响应快、适应性好和不受模型限制等优点[3]而被广泛用于风洞模型振动抑制。国际上NASA的RIVERS M B等针对共同研究模型 (CRM)设计了以12个压电陶瓷作动器为驱动装置的抑振器，将其安装于尾撑式风洞模型系统的天平与支杆之间，抑振效果较好[4]；国内也对该方向进行了相关研究，设计了基于比例、积分、微分(PID)、神经网络[5]、模型分析与系统辨识[6]等控制算法，这些控制算法分别对于各工况、变攻角风洞模型有一定的振动抑制效果。

压电陶瓷材料同时具有非线性、蠕变及迟滞等特性[7]。其中，迟滞特性对抑振效果影响最显著，会使压电陶瓷作动器的期望输出抑振力与激励电压间关系变为非线性，抑振力输出产生滞后，削弱抑振效果[8]。目前减小压电陶瓷材料迟滞非线性的影响方法很多。Preisach模型[9]能构建复杂的迟滞回线，但需要大量的数学运算；PI模型和改进PI模型[10]原理简单，但模型复杂，难以实现实时运算；运用拟合法建立迟滞曲线的拟合模型也常用，如多项式拟合模型[11]、神经网络模型[12-13]等，该方法简化了迟滞模型，且精度较高，适应性较强。

为了减小压电陶瓷作动器迟滞效应的影响，本文提出了一套基于压电陶瓷作动器神经网络模型的振动抑制方法。首先分析了风洞模型系统振动特性，通过模型质心加速度推算出压电陶瓷作动器期望输出抑振力；建立了压电陶瓷作动器期望输出抑振力-激励电压的神经网络模型，运用试验采集的输出抑振力-激励电压数据对网络进行训练，根据该模型设计了一种实时抑振力解算控制方法；最后通过地面试验验证了该控制方法的有效性。

1 风洞模型系统的动力学模型与抑振原理

1.1 系统动力学模型

风洞模型多采用尾部支杆支撑方式，风洞模型-测力天平-尾撑支杆在结构上组成了经典悬臂梁结构，如图1所示。

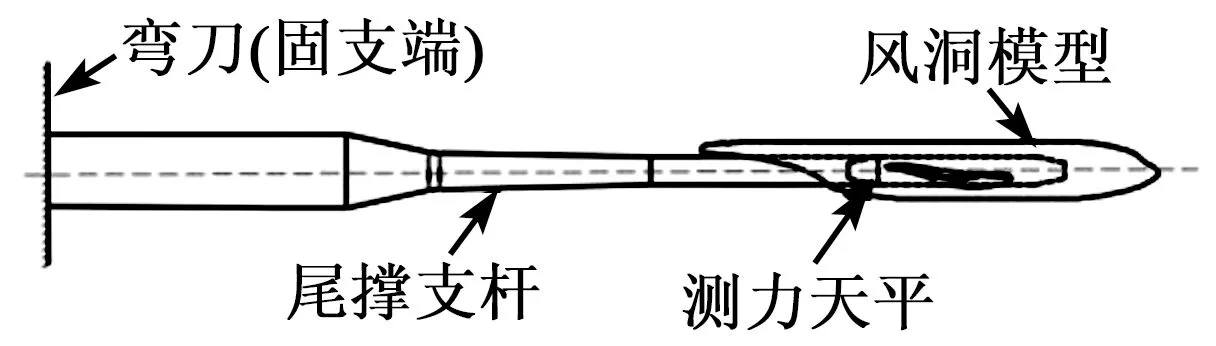
图1 风洞支杆模型系统简化图

模型与天平之间通过螺栓连接，天平与尾撑支杆之间通过销孔定位，锥面连接。尾撑支杆同样通过锥面连接与弯刀相连，弯刀可以上下移动来调节飞机模型在风洞中的位置，改变模型相对于风洞气流的攻角。在风洞实验中弯刀位置相对不变，可将弯刀视为悬臂梁的固支端。因此可将风洞模型系统看成质量-阻尼-弹簧系统，在风洞动态气流中易产生耦合发生振动。其振动方程可写为

(1)

1.2 振动抑制原理

在风洞模型变攻角测试试验中，不同位姿下风洞模型所受气动载荷不断变化，激励具有强随机性。为抑制该振动，在尾撑支杆的尾部直线部分加工安装槽，用于内嵌式安装压电陶瓷作动器；同时提出一套主动振动抑制系统方案。该系统的反馈信号采用风洞模型质心的加速度信号，通过控制器运算处理得出压电陶瓷作动器的激励电压信号，经放大后输出给压电陶瓷作动器，构成闭环控制系统，如图2所示，其中，A-A为压电陶瓷作动器处剖面图。

图2 主动振动抑制系统方案简图

根据风洞模型系统等效质量质心的惯性力产生的力矩，压电陶瓷作动器输出与其方向相反、大小相等的力矩，实现对风洞模型系统振动的控制。力矩等式有

Fp·lp=F·h

(2)

(3)

式中：Fp为系统等效质量质心的惯性力；lp为风洞模型质心到压电陶瓷作动器端面的距离；F为压电陶瓷作动器输出力；h为压电陶瓷作动器中心到截面轴线的距离。

由式(2)、(3)可推导压电陶瓷作动器的输出力为

(4)

2 压电陶瓷作动器神经网络建模

压电陶瓷材料属于典型的非线性材料，其输出特性存在非线性区域。其中，压电陶瓷非线性特性中最主要的是迟滞非线性，表现为在激励电压的上升和下降阶段输出呈滞回环形式。迟滞非线性使由压电方程推算的期望输出抑振力-激励电压关系不再准确，存在一定的误差，且迟滞非线性使常用的经典控制理论和现代控制理论都难以对其实施有效的控制[8]。

人工神经网络是一种模仿生物神经网络结构和功能的数学模型或计算模型，通过内部神经元节点的相互连接，达到处理信息的目的，且具有一定的适应性。其中BP神经网络能够学习和储存大量输入-输出模式映射关系，并且无需知道映射关系的数学方程，能够很好地拟合非线性模型。

压电陶瓷作动器的神经网络建模流程如图3所示。

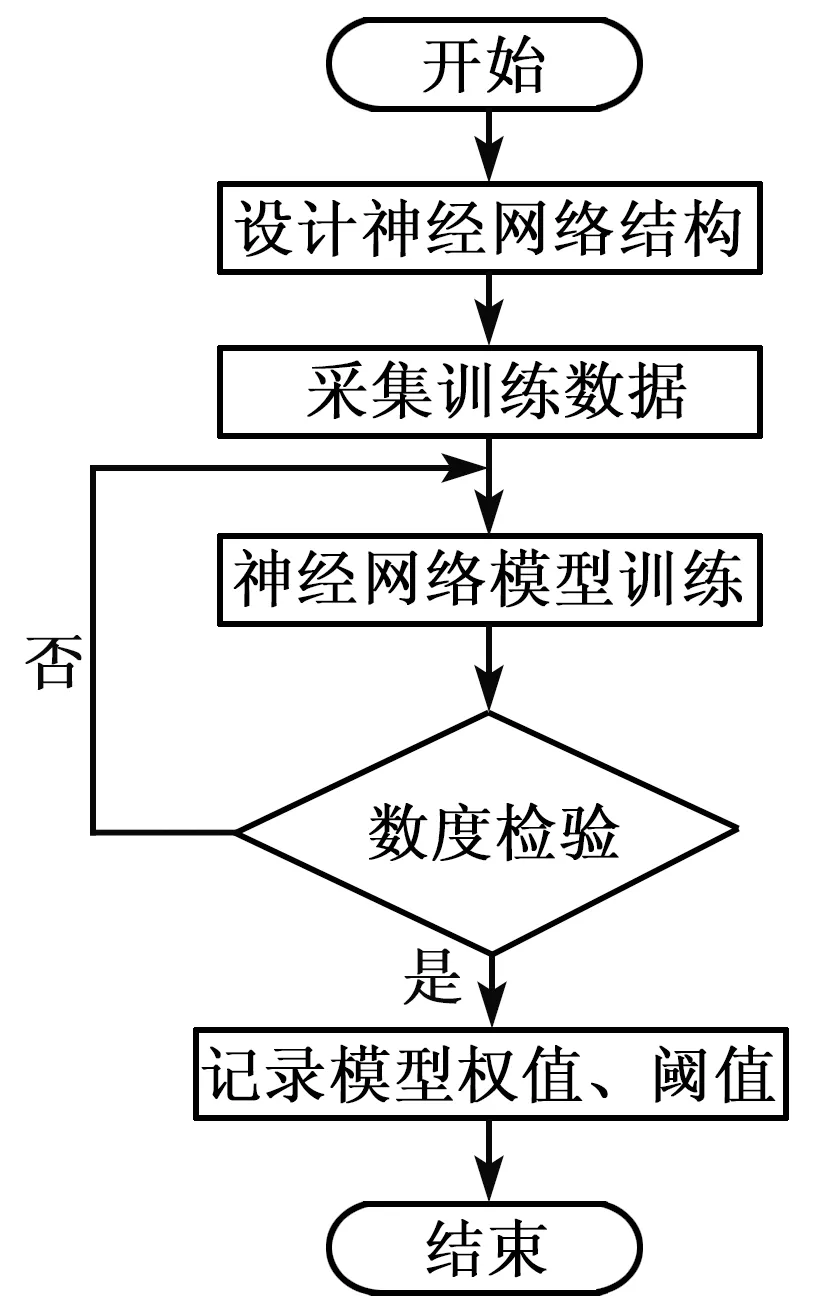
图3 神经网络模型建立流程图

2.1 压电陶瓷神经网络模型结构设计

一般来说，具有一个非线性隐含层加上一个线性输出层的网络可以很好地逼近任一非线性模型[13]。由于压电陶瓷迟滞特性也表现为抑振力输出，不仅与当前输入激励电压相关，还与历史输入激励电压有关，因此，该神经网络模型选用3层结构网络，输入层设置2个节点，分别为压电陶瓷作动器输出力Fn与上一次采样时的压电陶瓷作动器输出力Fn-1；输出层有1个节点，为压电陶瓷作动器激励电压Un，如图4所示。

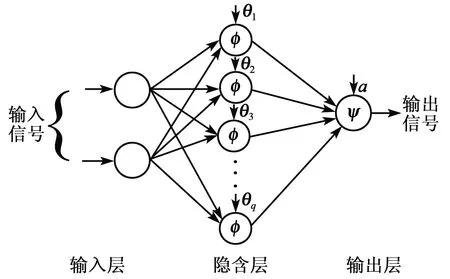
图4 典型3层BP神经网络结构图

2.2 实验系统、数据采集与模型训练

实验系统如图5所示，压电陶瓷作动器选用德国Physik Instrumente公司生产的未封装PICA Stack Piezo Actuators高压大力输出压电陶瓷作动器。数据采集及控制系统选用美国NI公司的控制器主机以及多种功能模块，其中PXI桥-输入-模块具有25 kS/s采样率。PXI-模拟-输出-模块是一款具有集成信号调理功能的通道间隔离模拟输出模块，该输出模块可以提供准确、同步的动态电压和电流输出。由于PXI-模拟-输出-模块的输出电压为0～10 V，无法直接驱动压电陶瓷作动器，因此，驱动环节需要对控制信号进行放大，故选用德国PI公司生产的功率放大器对控制信号进行放大。力传感器为高精度测力元件，具有0.1%的低误差率，可以通过虚拟仪器LabVIEW软件实现力学量单位的转换。

图5 实验系统图

调节压电陶瓷作动器预紧力，施加逐渐衰减的激励电压，根据单自由度系统受到单位冲量时的响应公式，激励电压可表示为

U=e-ξ·2πf·t·sin(2πf·t)

(5)

式中：ξ=1为风洞模型系统的阻尼比；f为激励电压的频率，为了在每个周期内有尽可能多的采样点，需要降低激励频率，取f=1 Hz。

编写LabVIEW程序实时读取并存储激励电压值与在此激励下压电陶瓷作动器输出力的值。采集的激励电压数据与压电陶瓷作动器输出力数据如图6所示。其中采样频率500 Hz，共1 000个数据点，组成4个依次减小的迟滞回环。

图6 激励电压与压电陶瓷作动器输出力关系图

将采集的数据按照神经网络结构的输入、输出组成训练数据。为了加快数据收敛与防止数据饱和，在训练前需要对数据进行标准化，将数据化为[0,1]，公式如下：

(6)

式中：Fn为样本值；Fmax、Fmin为训练样本的最大值和最小值；F′n为归一化后的训练值。

之后设置神经网络参数，包括最大训练次数、目标精度、学习速率等。最大训练次数和目标精度决定训练算法的终止条件，当训练算法的训练次数达到最大训练次数或训练精度小于目标精度时，训练终止。

2.3 压电陶瓷神经网络模型建立

神经网络结构中隐含层神经元数的范围可由下式[12]确定：

(7)

式中：n为输入层神经元个数；m为输出层神经元个数；c为1～10的整数。

对不同隐含层神经元个数的模型分别训练，由式(7)可计算得隐含层神经元个数为3～12，分别记录神经网络的均方误差如表1所示。选择神经网络隐含层神经元个数为5，其拟合图像如图7所示。

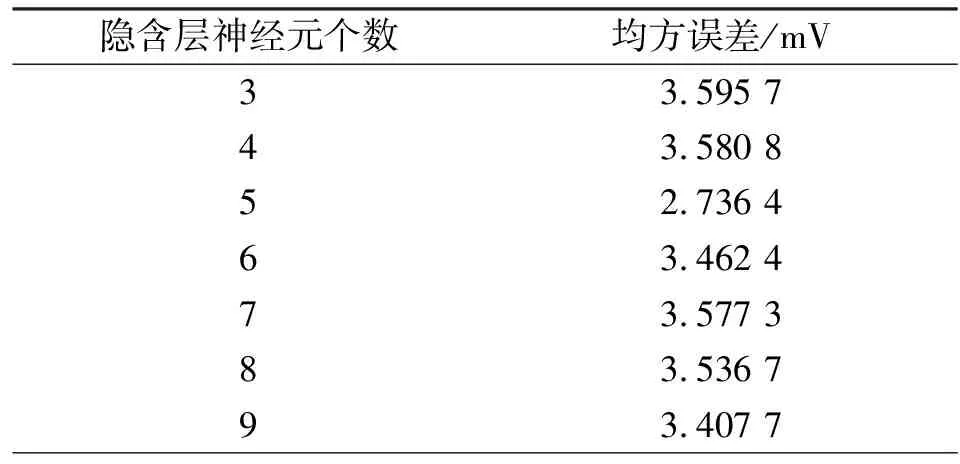
表1 隐含层神经元个数对精度的影响

续表

隐含层神经元个数均方误差/mV103.118 9113.452 1123.137 1

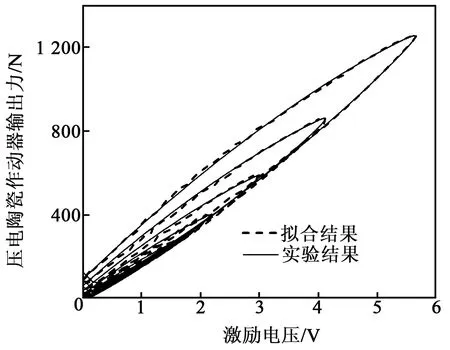
图7 神经网络预测输出与期望输出比较

最终建立了双输入、单输出，隐含层有5个神经元的压电陶瓷BP神经网络模型，各个权值和阈值如表2所示，其中，ωi1为隐含层到输入层神经元Fn的权值，ωi2为隐含层到输入层神经元Fn-1的权值。

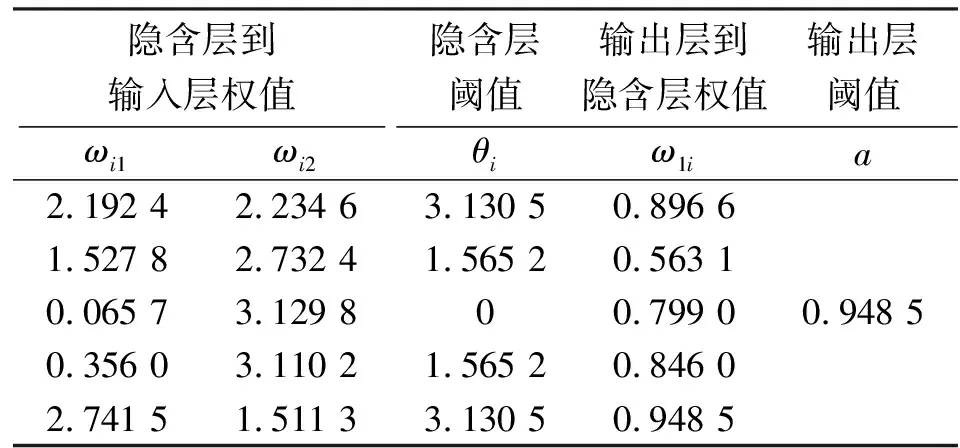
表2 压电陶瓷神经网络模型参数

3 基于压电陶瓷作动器神经网络模型的抑振算法

3.1 控制算法

在飞机模型的风洞试验中，飞机模型所受载荷受风速、攻角等因素影响变化很大，而且受到风洞环境影响，气动载荷存在不确定性，故而需要设计主动抑振的控制算法对压电陶瓷作动器进行实时控制。控制算法示意图如图8所示。

图8 控制算法示意图

3.2 基于压电方程的线性控制器

压电陶瓷作动器由压电材料构成，假设其为线性材料，第一类压电方程为

(8)

式中：S为压电陶瓷作动器应变；A为其横截面积；U为加载电压；ap为陶瓷介质层的厚度；S33为弹性柔度常数；d33为压电应变常数。

由式(8)可以推导出风洞模型系统中压电陶瓷作动器的加载电压为

(9)

3.3 基于压电陶瓷作动器神经网络模型的非线性控制器

由于压电陶瓷材料具有迟滞等非线性特性，使用线性控制算法控制存在很大误差，难以应用于此控制系统，故引入压电陶瓷作动器神经网络模型来减小此误差。

根据神经网络模型结构确定输入的信息为Fn、Fn-1，由式(4)可得：

(10)

输入信息经神经网络模型运算后，隐含层神经元的输出为

yi=φ(ωi1·Fn+ωi2·Fn-1+θi)

(11)

输出层神经元输出，即控制器的输出激励电压为

(12)

4 风洞模型系统地面试验

4.1 试验平台

本文采用的风洞模型系统如图9所示，后部安装了4个内嵌式压电陶瓷作动器，且呈正交分布，作为抑振器。其中，利用加速度传感器对模型质心俯仰方向的加速度进行测量作为控制信号。本文对风洞模型系统进行锤击试验验证抑振算法的有效性与鲁棒性。

图9 风洞模型系统地面试验图

4.2 锤击试验结果与分析

对风洞模型系统进行锤击试验，锤击位置在风洞模型质心，分别对比了控制器关闭、压电方程线性控制器和压电陶瓷神经网络模型控制器(简称ANN模型控制器)3种情况下风洞模型质心的加速度响应，如图10、11所示。

图10 未抑振、压电方程线性控制和压电陶瓷神经网络模型控制下锤击响应对比

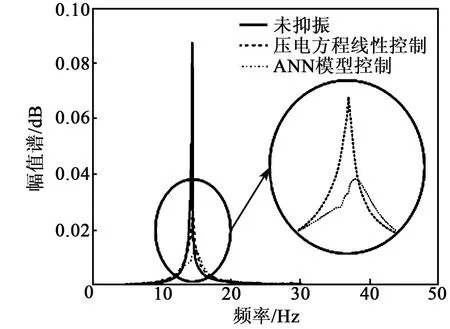
图11 未抑振、压电方程线性控制和压电陶瓷神经网络模型控制下频谱响应对比

由图10、11可知，未抑振、压电方程线性控制和压电陶瓷神经网络模型控制下，振幅衰减到最大值10%的时间分别为4.40 s、1.12 s和0.51 s ；半功率法计算阻尼比分别为0.005 2、0.017 1和0.044 2。压电陶瓷神经网络模型控制增大了风洞模型系统的阻尼比，加快振动衰减，与未抑振、压电方程线性控制相比，其衰减时间减小了88.41%与54.46%，阻尼比增大了7.50倍与1.58倍。

5 结束语

本文针对风洞模型系统在脉动气流下的振动问题，分析了风洞模型系统振动特性，建立了内嵌式压电陶瓷作动器的主动振动控制系统，通过模型质心加速度推算出压电陶瓷作动器期望输出抑振力。为了消除压电陶瓷材料迟滞特性的影响，建立了压电陶瓷作动器期望输出抑振力-激励电压的神经网络模型，并根据该模型设计了一种实时解算加速度为激励电压的控制方法，实现了对风洞模型系统俯仰方向振动的抑制。该控制方法减小了因压电陶瓷材料迟滞特性引起的输出信号偏移，相比于压电方程线性控制，其具有良好的实时性和鲁棒性。该方法能够优化压电陶瓷作动器输出性能，对于下一步风洞试验研究有较大参考价值。