竹材梯度结构对弯曲力学性能的影响

马弘帅

(河北经贸大学 石家庄 050061)

竹材是一种典型的天然梯度材料，其维管束分布密度由内向外连续增大，竹壁密度呈现显著的梯度分布，组织向外愈加致密化[1-4]。梯度结构赋予了竹材优良的抗弯性能，在纤维体积分数一定的条件下，梯度材料比均质材料的抗弯模量高30%[5]；竹材弯曲曲率是山毛榉的2倍、云杉的3.5倍[6]。由此可见，竹材梯度结构对力学性能影响显著。美国德雷塞尔大学[5]提出一种梯度形状因子(gradient shape factor)分析模型，描述了梯度结构对圆竹抗弯性能的影响规律，认为在工程领域未充分利用竹材的优良梯度特性，竹材除了在工程领域作为传统结构材应用之外，还可以用于新型的梯度材料领域。

然而，竹纤维的不规则分布导致竹材宏观力学的离散性，同株、同节、等尺寸的竹材在弯曲条件下的极限载荷仍有较大的离散性，且和纤维体积分数无显著线性关系；并且当锯切为竹条后，呈现不对称的弯曲行为，这种力学特征和其自身梯度结构密切相关。在组织层面，竹材维管束呈现显著的梯度特征[7]，其大小和密度与纵向部位、径向部位均有密切关系。研究人员提炼出一系列的结构影响因子——维管束组织比量、维管束面积、维管束个数、维管束长短轴之比等，对这些因子进行了分布描述和数理统计，发现维管束密度沿径向从内到外呈增大趋势。这些研究积累了大量实验数据，很好解读了竹材结构。但是，前人研究由于实验条件受限，未对竹材维管束进行量化表征。因此，本文基于梯度结构理论的组成分布函数，结合具有竹材属性的梯度结构因子，获得竹材特有的梯度指数，并对竹材非对称的弯曲力学行为进行测试分析，以期揭示竹材结构与弯曲力学性能之间的关系。

1 材料与方法

1.1 试验材料

试验以采自福建省的4年生毛竹(Phyllostachysedulis)为材料。竹材竹壁厚度约10～12 mm。选取离地约1.5 m处的整竹节，参照国家标准GB/T1929-2009《木材物理力学试材锯解及试样截取方法》加工弯曲模量试样，试样尺寸为6 mm × 20 mm × 140 mm。参照国家标准GB/T15780-1995《竹材物理力学性质试验方法》进行测试和计算，加工和测试示意图见图1。

1.2 梯度结构表征

制备40组样品，将每组竹材端面用细砂纸抛光，以便快速获得精细图像。然后采用EPSON PERFECTION V850 PRO高精度扫描仪对竹材试样的横截面A、B两端分别进行扫描，图像分辨率可以达到9 600 dpi。

注：(a)竹青侧受压；(b)竹黄侧受压。图1 竹材试材锯解及弯曲力学测试示意图

将上述图片导入到YOLOv3 模型软件中，进行二值化处理，获得二值化图片(图2)。与传统二值化图片不同之处在于，每个维管束是根据坐标信息进行抓取、重聚、还原的，排除了环境干扰，比传统二值化图片更清晰准确。采用移动平滑积分法对二值化图片进行计算，获得纤维鞘面积(图2中黑色部分)及组织比量等。然后对图像进行分层处理，从竹青到竹黄分为16层。由于软件识别技术的原因，图像两端的数据会有误差，所以分析时去掉两端数据，取14层数据进行分析，获取每层纤维鞘的面积。

1.3 力学性能测试

试样加工完成后，置于气干环境中平衡，平衡2周后进行力学性能测试。弯曲力学性能测试仪器为Instron 5582万能力学试验机，测试指标有静曲强度、弹性模量等。弹性模量的取值区间为20%～40%Pmax。在40组样品中，20组采取竹青侧加载方式，另外20组采取竹黄侧加载方式。

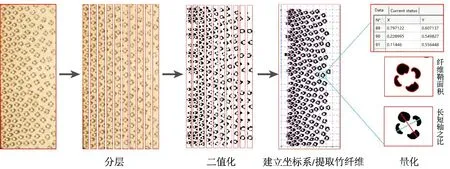
注：(a)竹青侧受压；(b)竹黄侧受压。图2 软件处理图像示意图

2 结果与分析

2.1 基本密度

在对竹材的梯度结构和力学性能进行测试前，首先测试了试验用竹材的密度。结果显示，竹材的平均密度为0.713 3 g/cm3，标准差为0.05，方差为0.003。表明这组竹材具有较均一的物理性能。

2.2 竹材维管束比量的梯度变异

表征梯度结构要确定材料组分随着坐标的变化情况[8]。目前在功能梯度材料领域较有代表性的描述组成分布的函数有Wakashima函数[9](图3)，其原理是设某种梯度材料由组元A和组元B构成，其成分沿x方向呈一维连续变化，则组元A的体积分数是x的一元函数：

(1)

式(1)中：h表示梯度材料的厚度，n为梯度率，也称梯度指数。

图3 梯度结构Wakashima模型(a)与维管束沿竹材厚度方向的数值模型(b)。

竹材可以看作由竹纤维和薄壁组织共同组成的梯度材料，维管束比量沿竹材厚度方向同样呈一维连续变化，可以用Wakashima函数进行模拟。设竹青与竹黄间中心点为零点，f(x)是竹材物理性质参数的函数，沿竹材的厚度方向变化。向竹青方向为正，向竹黄方向为负。采用YOLOv3 模型软件对各层维管束面积及比量进行统计，然后代入公式(1)中进行拟合。图4是毛竹维管束沿径向梯度分布的曲线，维管束组织比量从竹黄到竹青呈上升趋势，但是曲线斜率越来越小，属于下凹型曲线。拟合后的结果显示，毛竹材的维管束梯度分布指数n=2.28。

图4 竹材维管束组织比量分布

黄盛霞[10]在研究从竹青到竹黄的纤维组织比量时，认为组织比量沿径向呈线性变化。周爱萍等[7]在研究毛竹维管束分布时，发现维管束密度沿毛竹径向的规律变化分为3个阶段，呈先增加，然后平缓，最后增加的趋势，认为维管束密度在距竹黄约0.8～1.2 cm处的增长速度最快，距竹青越近，维管束越密集。陈冠军[11]研究了11种竹材纤维组织比量，发现不同竹种的纤维径向梯度分布模式不同，大体分为上凸型、近S型、下凹型；其中毛竹属于近S型。这些研究结果的区别与竹材年龄、取材位置、取样形状等均有关系。

2.3 维管束形状变化

从竹青到竹黄，竹材维管束形状也存在一定的梯度变异性。竹青侧的维管束形态较小，分布较密集；竹黄侧的维管束形状较大，分布也较稀疏。为了更清晰的表达维管束形状的变化，以长径比(图5)为指标进行描述。从竹青到竹黄分成4层，每层取15个完整的维管束图片，计算其长径比。如图6所示，从竹青到竹黄，维管束长径比呈现明显下降的趋势，靠近竹青侧的维管束长径比较大，靠近竹黄侧的维管束长径比较小，形状更趋近于圆形。

图5 维管束长径比定量测试

图6 从竹青到竹黄的维管束长径比变化趋势

2.4 竹材非对称弯曲行为

图7是竹黄侧加载和竹青侧加载2种不同方式下的应力应变图。从图中可以看出，在竹青侧加载模式下，曲线迅速上升，弹性段持续一段时间后，进入塑性阶段，到达顶点后线段呈垂直下降趋势，说明材料为典型的脆性断裂；在竹黄侧加载模式下，弹性段相对较短，很快进入塑性阶段，且持续了很长时间，到达顶点后，曲线出现波纹状，缓慢下降一段时间后才出现平滑垂直下降的趋势，说明材料为典型的延性断裂。

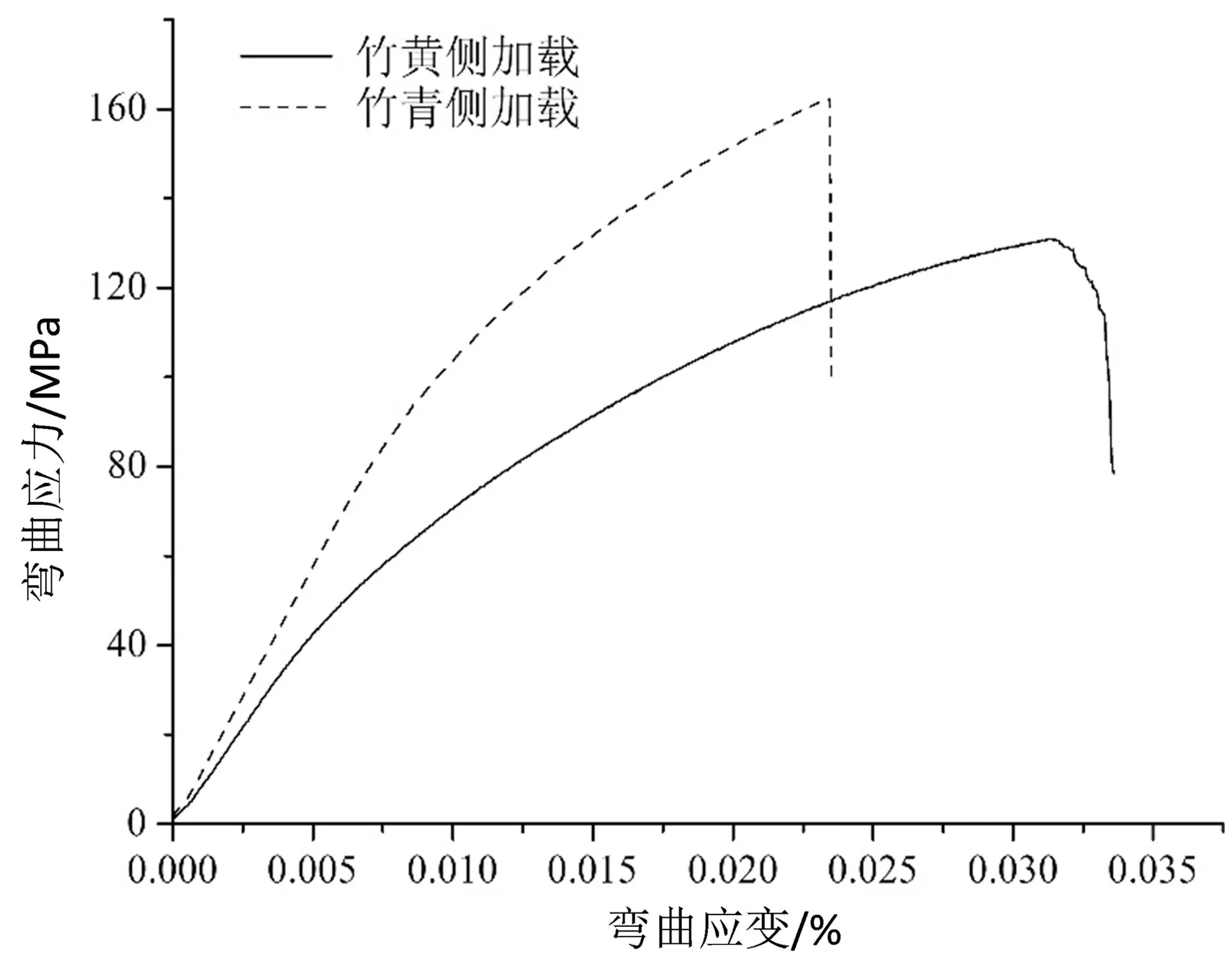
图7 不同加载方式下弯曲应力应变情况

对比2种加载模式下的弹性模量，当竹黄侧加载时为8.062 9 GPa，当竹青侧加载时为9.088 5 GPa。竹青侧加载时的弹性模量大于竹黄侧加载时的弹性模量，这与Obataya[6]、Habibi[12]等人的结论一致，这与竹材的梯度结构关系密切。竹材是由纤维和薄壁组织组成的天然梯度材料，这种梯度分布也引起了竹材厚度方向上的梯度力学行为模式。如图1(a)所示，在竹青侧加载方式下，受压侧纤维较多，受拉侧薄壁组织较多，当受力加载时，纤维较多的一侧承受压应力，薄壁组织较多的一侧承受拉应力，此时竹材的弯曲模量表现较大，弯曲应变较小；在竹黄侧加载方式下，如图1(b)所示，受压侧纤维较少，受拉侧纤维较多，当受力加载时，薄壁组织较多的一侧承受压应力，纤维较多的一侧承受拉应力，此时竹材的弯曲模量表现较低，弯曲应变较大。因此，加载方式对竹材的弯曲力学影响显著，在竹青侧受压、竹黄侧受拉的情况下，竹材的弯曲模量最大；在竹黄侧受压、竹青侧受拉的情况下，竹材的弯曲韧性最好。

3 结论

1) 拟合了毛竹维管束沿径向梯度分布的曲线，发现该曲线属于下凹型曲线，毛竹材的维管束梯度分布指数n=2.28。

2) 用长径比描述了维管束形状的变化。从竹青到竹黄，维管束长径比呈现明显下降的趋势，靠近竹青侧的维管束长径比较大，靠近竹黄侧的维管束长径比较小，形状更趋近于圆形。

3) 对比了竹黄侧加载和竹青侧加载2种模式下的竹材弯曲力学性能，发现加载方式对竹材的弯曲力学影响显著，在竹青侧受压、竹黄侧受拉的情况下，竹材的弯曲韧性最好；在竹青侧受拉、竹黄侧受压的情况下，竹材的弯曲模量最大。