基于状态空间模型的飞行器装配误差敏感度研究

孙崇飞 李 欣 朱一鸣 尚建忠 罗自荣 何立军

(1.国防科技大学智能科学学院，长沙410073;2.山东理工大学机械工程学院，淄博255049;3.国防科技大学脉冲功率激光技术国家重点实验室，合肥230037;4.曼彻斯特大学机械、航天与土木工程学院，曼彻斯特M17JR;5.陆军勤务学院训练基地，武汉430035)

0 引言

飞行器是人类探索未知领域和利用自然资源的重要工具［1-2］。角偏误差是飞行器多舱段精密装配的核心指标，对控制舱体内传感器电气轴线安装精度和确保飞行器正常工作具有重要意义［3-6］。在飞行器制造过程中，不同误差源对最终装配的影响程度不同，其对应精度控制的实现难易程度也不同。通过分析每个误差源的敏感度、重点削减敏感度较大的误差源，有助于降低飞行器制造成本、提高飞行器性能特性。

飞行器装配精度主要受装夹误差和制造误差等影响，装配精度分析的重点是对误差进行建模和分析。根据配合特征和夹具对装配的影响，把装配问题分成Ⅰ型装配和Ⅱ型装配两大类。Ⅰ型装配中零件位置仅由配合特征决定，不包括夹具定位误差和工位内部相互作用。文献［7 -11］研究了Ⅰ型装配问题。MANTRIPRAGADA 等［12］用运动学关节概念定义运动约束，以运动学原理和变换为主要方法分析零件间的误差累积。Ⅱ型装配中零件位置受装配特征和夹具的共同影响。Ⅱ型装配在汽车与飞机制造工业中比较常见，其典型研究见文献［13 -18］。

误差敏感度表示不同装配误差对装配最终效果的影响程度，是评价装配精度重要指标。目前，装配误差敏感度的相关研究取得了一定进展。LIU等［19］将误差描述扩展到三维空间，构建了三维误差传递过程状态空间模型，主要将定位元件误差作为误差源。QURESHI 等［20］在公差分析过程中将误差描述为一个间隙量，便于过度约束的公差分析。ANSELMETTI［3］提出基于“雅可比-矢量对”模型，实现了雅可比矩阵和矢量对方法的综合。HUANG等［21］提出了基于3-2-1 定位夹具的多工位装配工艺误差传递模型，形成面向三维空间的误差装配模型。LAPERRIÈRE 等［22］将三维空间几何变化用6 个标量方程表示，以此实现公差分析，但未考虑装配基准在误差传递中的作用。

本文提出一种包含关键产品特性(Key product characteristic，KPC)和关键控制特性(Key control characteristic，KCC)的装配误差敏感度量化分析方法。该方法基于状态空间模型对飞行器的多舱段装配过程进行量化追踪，以控制和补偿其装配精度。

1 装配误差敏感度表示

飞行器的性能特性主要取决于实现其产品功能的关键设计特征。在装配领域，KPC 相当于关键设计特征，KPC 可以通过提高夹具定位精度和几何尺寸误差进行控制。而夹具定位精度和夹具几何尺寸误差主要包含于KCC。KPC 和KCC 在误差传播模型中以点的形式存在，可记为KPCs 和KCCs。在刚体多工位装配过程中，KCCs 误差对KPCs 几何精度的影响依赖于各工位上夹具几何尺寸和工位间夹具的改变。

用γ(i)来表示KPC 误差与KCC 误差的比值，对应装配状态空间模型的系统矩阵由工位之间定位的变化、单独工位上定位夹具的几何因素和KPCs的选择决定。如果把工位标号i 视为动态系统的时间，则状态空间系统模型可描述为一个线性时变的随机过程。因此，可以把动态系统灵敏度分析的方法应用到多工位装配过程中。装配过程中的灵敏度分析可理解为系统对特定误差输入的响应，灵敏度指标即类似于传统控制理论中的系统增益。

图1 为N 个工位装配过程，KPC 误差可表示为

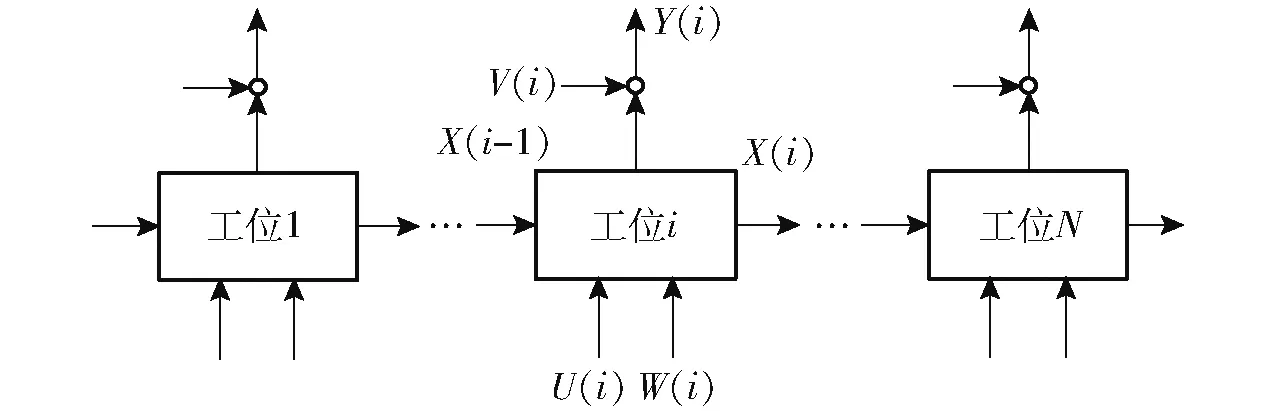
图1 N 个工位的装配过程Fig.1 Assembly process of N positions

误差向量σ2out，其组成元素为ΣY的对角元素。KCC误差的输入可用夹具、工位和系统3 个不同角度来考虑，相应3 个级别的灵敏度指标为:

(1)特征级别灵敏度指标Sip为

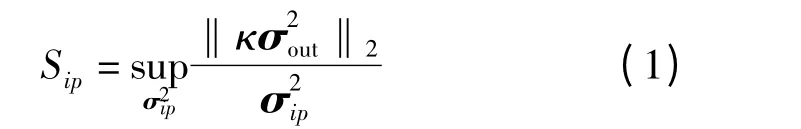
式中 κ——加权系数，决定KPC 误差的重要性

‖·‖2——欧几里得范数

σ——误差

i——工位序号

p——定位点序号

Sip指出了第i 个工位上的第p 个定位特征对KPC 误差的贡献，相当于一个单输入多输出(Singleinput multi-output，SIMO)系统的增益。它决定了对KPC 误差贡献最大的关键定位特征。

(2)工位级别灵敏度指标Si为

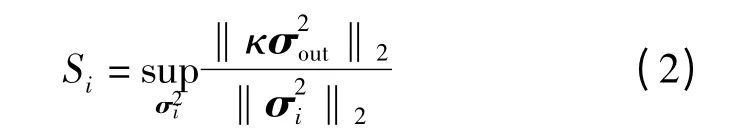
其中，Si指出了在第i 个工位上夹具的所有定位特征是如何共同影响KPC 误差的，相当于一个多输入多输出(Multi-input multi-output，MIMO)系统的增益。它决定了对KPC 误差贡献最大的关键工位。

(3)系统级别的灵敏度指标So为

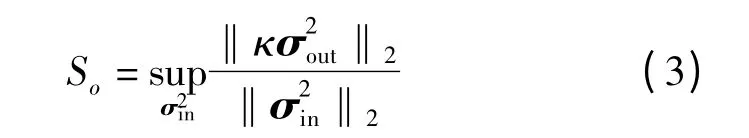
上述Sip、Si和So是KPC 误差与KCC 误差的比值，相当于单位KCC 误差输入的KPC 误差。3 个单位KCC 误差有区别:对于单独的定位特征，单位KCC 误差是=1;对于单独工位，单位KCC 误差是夹具所有定位特征共同的影响，即‖σ2i‖2=1;对于整个系统，单位KCC 误差是所有工位联合的影响，即‖‖2=1。一个小于1 的敏感度系数意味着KPC 误差等级可以比KCC 误差等级更低。相反，一个大于1 的敏感度系数说明了系统放大了输入误差。大多数的多工位系统的敏感度系数都会大于1，然而期望得到敏感度系数较小的误差系统。因此，需要比较并分析这些敏感度系数，找出敏感工位或敏感夹具来优先满足其要求，进而减小最终误差。

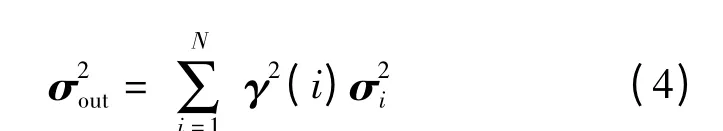
其中γ2(i)中的元素是矩阵γ(i)对应元素的平方，即

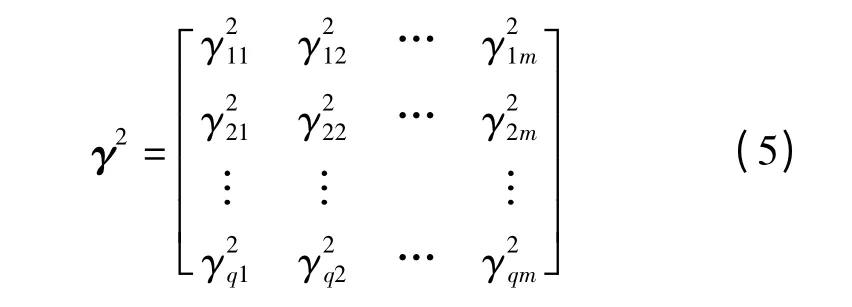
根据Sip的定义，假设每次在整个过程中只有一个误差源，则在所有KCC 输入中只有向量σ2i是非零的，它只包含一个非零元素σ2ip。因此，第i 个工位上的第p 个定位点的敏感度指标Sip可以表示为

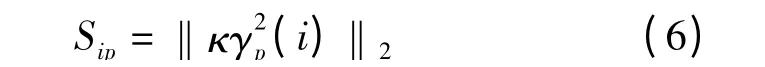
根据Si的定义，假设每次只有一个工位有误差输入，但是在每个工位中，会同时有多个定位特征对做出贡献，在所有KCC 输入中只有向量σ2i是非零的。因此，Si可以表示为

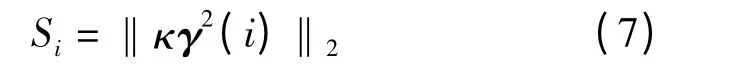
系统级别的敏感度考虑了所有KCC 误差输入的可能组合，包括工位内部和工位之间。因此，它代表了整个过程系统对于KCC 输入的敏感度。So可以表示为

当然，也可认为夹具敏感度系数是特殊的工位敏感度系数及系统敏感度系数，即考虑在相应的工位内和过程中找出最大的夹具敏感度系数分别作为工位敏感度系数和过程敏感度系数。夹具敏感度系数则代表过程对单一误差输入的响应，而实际的工位敏感度系数Si和系统敏感度系数So表示多个误差输入同时作用系统的响应。这两种方法在定义上有所不同，需根据实际情况而定。

2 基于飞行器模型的敏感度理论计算

以一个三舱段飞行器的装配过程为例，对其误差敏感度进行计算和验证。装配过程分为3 个工位，其装配示意图及装配顺序如图2 所示。

与更多的涉农高校、科研院所建立本地化推广机构，与农科院系统协同合作，促进先进农业技术、成果在常州地区的转化和推广；加快江苏省农村科技服务超市建设，每年新增1～2家超市分店，3～5家便利店，让科技服务的触角延伸到乡镇各个角落；加强5家省现代农业科技园建设和管理，提升现代农业科技园创新创业和服务能力，积极为园区招引优质企业。

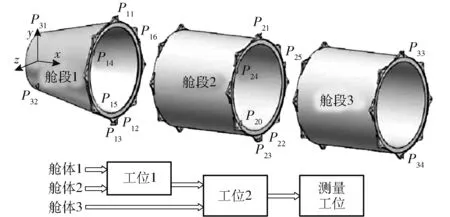
图2 三舱段飞行器的装配实例Fig.2 Application example of three-section aircraft assembly

定义装配过程中的KCC 点P1～P6。其中，零件定位点坐标分别为(240，135，0)、(240，-135，0)、(240，-90.7，-100)、(540，135，0)、(540，135，0)和(540，125.4，50)，测量点M1～M4坐标分别为(0，95，0)、(0，- 95，0)、(840，135，0)和(840，-135，0)，单位均为mm。

夹具的可能定位顺序如表1 所示。为简化分析，取所有KPCs 的加权系数均为1。

装配过程中，有2 个装配工位和1 个测量工位，即N=3。测量工位应排除夹具的影响，因此其夹具的输入误差远小于其他工位，认为是零。而其他两个工位上夹具的输入误差U(1)、U(2)不能忽略。定义测量值为舱体1 与舱体3 的X 轴向角偏误差，以第2 种装配顺序为例，装配过程的状态空间模型表达式为

表1 三舱段飞行器的装配顺序Tab.1 Aircraft assembly sequence

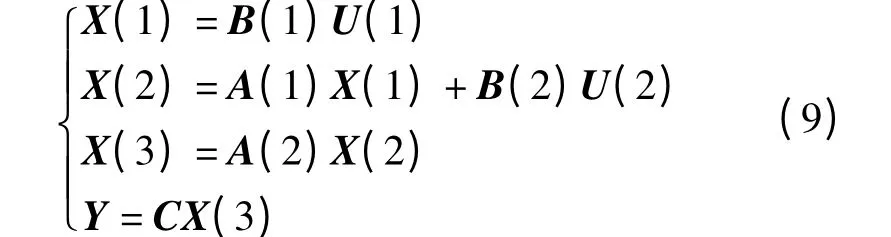
其中A、B、C 和U 可以由零件定位点和测量点已知坐标值计算得到，进而可得

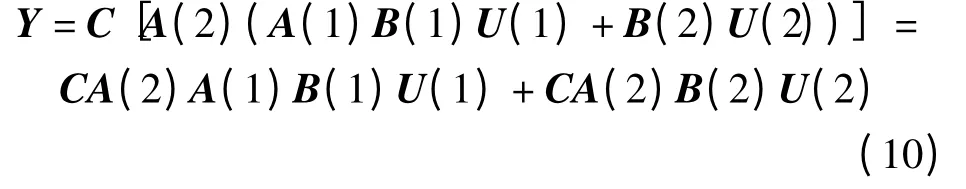
因此，γ(1)= CA(2)A(1)B(1)，γ(2)=CA(2)B(2)。

各工位误差对装配总误差贡献率计算式为

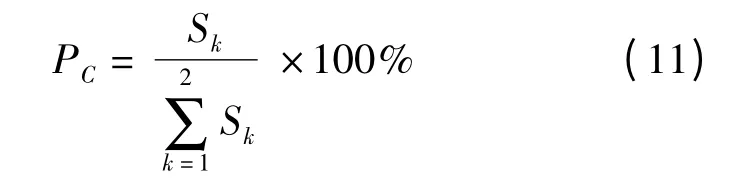
由式(7)、(11)求得该装配顺序下的工位级敏感度指标及其贡献率，如表2 所示。

表2 工位级敏感度指标及其贡献率Tab.2 Position-level sensitivity index and its corresponding contribution rate

由式(6)可求得特征级敏感度指标。每一个工位上都有2 个独立的配合特征。工位1 上舱体1 后端面和舱体2 前端面的特征级敏感度指标均为15.97%，工位2 上舱体2 后端面和舱体3 前端面的特征级敏感度指标均为34.03%。

3 基于蒙特卡洛方法的装配误差敏感度分析

当前基于数值仿真的刚性体装配误差分析已开始用于3DCS 等商业软件，其在前向设计仿真和容差分析等方面具有明显优势。蒙特卡罗(Monte Carlo)方法又称为随机模拟(Random simulation)方法，以概率统计论为理论基础，通过随机变量抽样对数学问题或工程技术问题进行分析。其计算方法及程序结构相对简单，适应性强，可直接模拟求解，能替代设计过程中的部分真实试验。本文采用蒙特卡罗方法对多舱段飞行器装配误差敏感度进行分析和验证。

建立蒙特卡洛仿真所需的飞行器模型，如图2所示。该模型的装配采用基于虚拟夹具的3-2-1 定位法定位，每个配合面上定义包括两定位销孔在内的6 个定位点，如图3 所示。

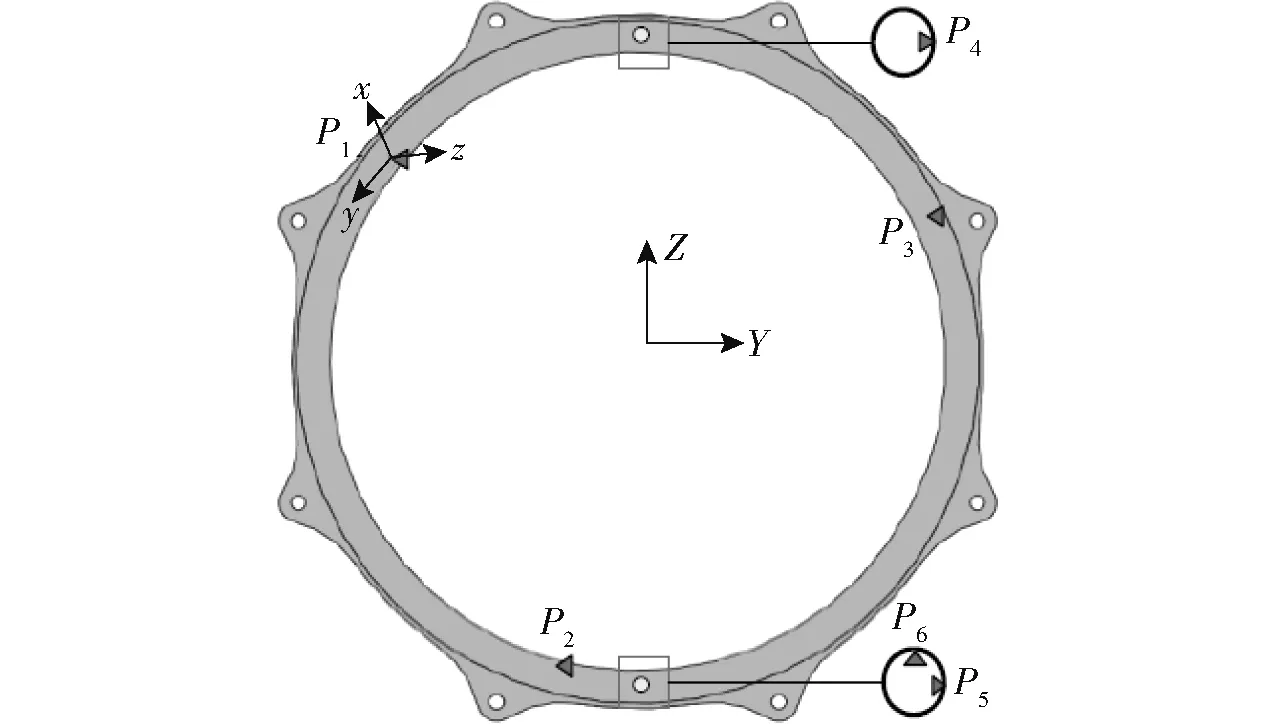
图3 舱体一面两孔的定位方式Fig.3 Positioning method of two-hole-one-side of section

设定模型的形位公差、各连接安装面的平面度误差和垂直度误差均为0.01 mm，平面度误差和垂直度误差都是线性公差。平面度公差如图4 所示。把连接面看作多个离散点的组合，连接安装面的形位公差等价为离散点在某个方向上相对于名义位置的偏移量。

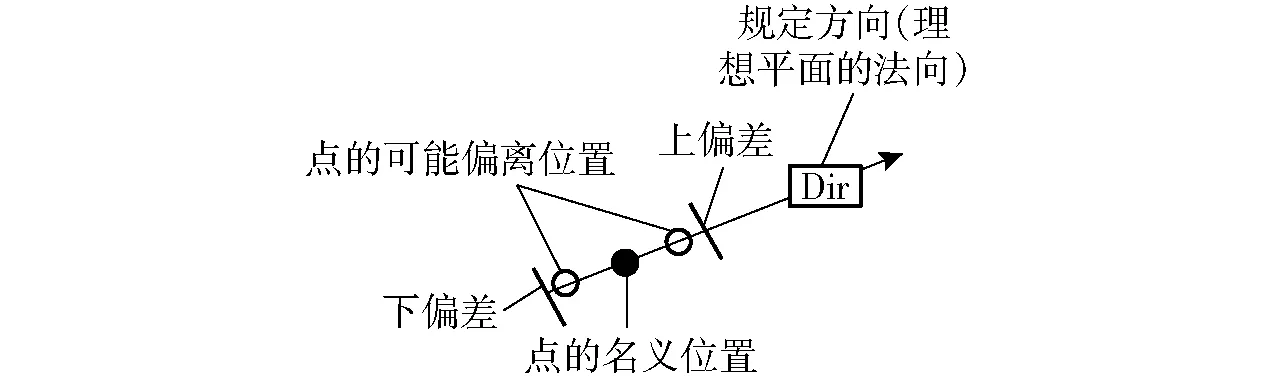
图4 平面度公差Fig.4 Flatness tolerance

选取每个连接安装面上两个定位销孔和螺栓连接孔之一为装配特征，选取其中心点为描述连接安装面形位公差的离散点。设定每个点沿连接安装面法向量方向的偏移量服从正态分布N(0，0.01)。

位置度公差如图5 所示。设定各连接安装面上两定位销孔的位置度公差为0.01 mm，位置度公差为圆域公差。偏离范围为一个以点的名义位置为圆心、公差为半径的圆域。

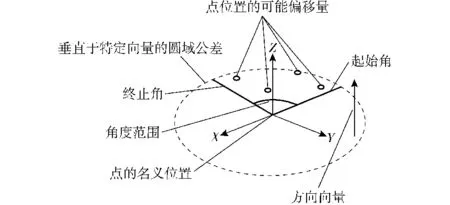
图5 位置度公差Fig.5 Position tolerance

设定两定位销孔的位置偏移量服从正态分布N(0，0.01)。定义图2 中舱体1 与舱体2 的X 轴向与Y 轴向角偏误差为测量值，进行2 000 次仿真，结果如图6 所示。考虑到装配顺序会对装配结果造成影响，在仿真中定义装配顺序为首先装配舱体1 和舱体2，再将其作为子装配体与舱体3 装配。

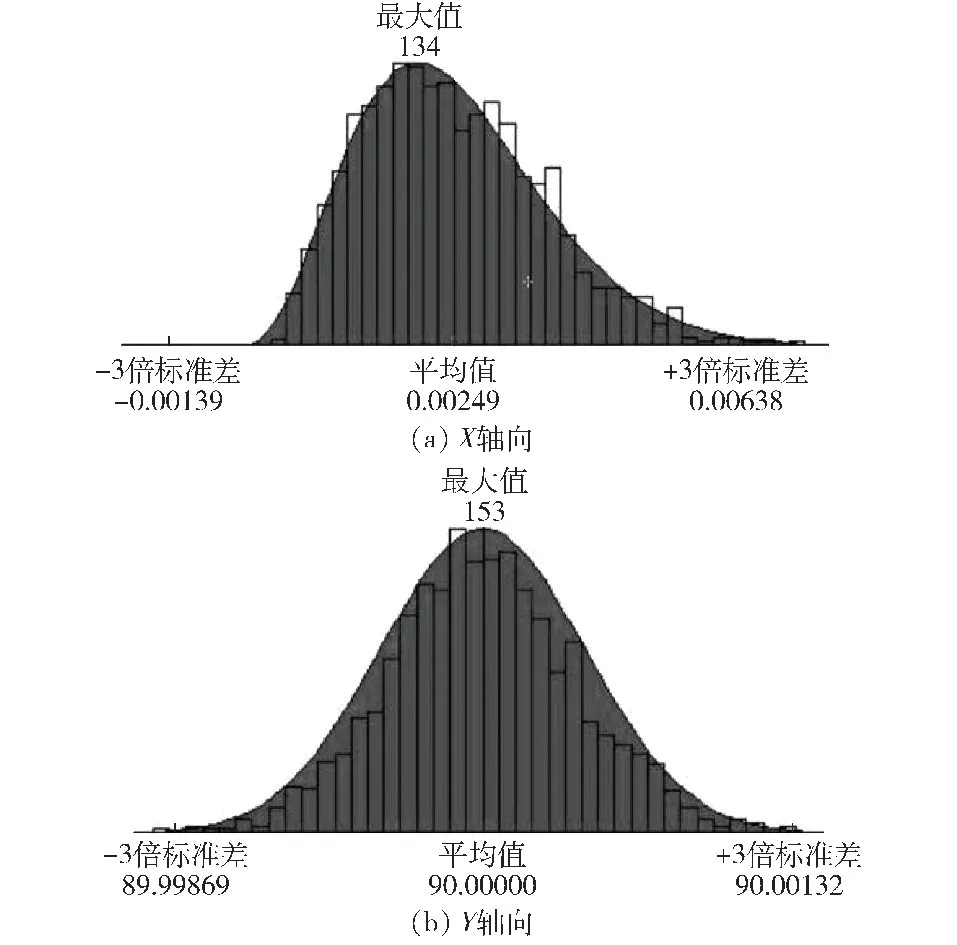
图6 舱体1 与舱体3 的角偏误差仿真值分布Fig.6 Angular deviation error distribution of section 1 and section 3

以舱体1 与舱体3 的X 轴向角偏误差为测量值时，舱体2 前端面对其影响最小，特征级敏感度指标为16.09%;其次为舱体1 后端面对结果的影响，敏感度指标为17.03%;舱体2 后端面的平面度与垂直度对结果的影响可达33.16%;对装配结果影响最大的是舱体3 前端面的平面度与垂直度，其特征级敏感度指标略大于舱体2 后端面，为33.72%。

对理论分析和蒙特卡洛仿真的计算结果对比可得，理论分析得出的4 个配合特征面敏感度指标与蒙特卡洛仿真得出的4 个配合特征面敏感度指标的误差最大为6.05%。对理论表达式与蒙特卡洛仿真计算得到的特征级敏感度进行对比验证，验证了理论方法计算飞行器多舱段装配误差敏感度的正确性。此外，当以舱体1 与舱体3 的Y 轴方向的角偏误差为测量值时，舱体3 前端面和舱体2 后端面两个定位销孔的位置度对其影响最大，影响率为37.48%;其次是舱体1 后端面和舱体2 前端面两个定位销孔位置度的影响，其值为12.52%;分析还得出，所有连接安装面的平面度与垂直度误差对舱体1 与舱体3 的Y 轴方向的角偏误差影响为0。

4 结束语

提出了一种包含关键产品特性和关键控制特性基于状态空间模型的装配误差敏感度量化分析理论方法，对飞行器多舱段精密装配过程中的误差敏感度分为特征级、工位级和系统级，并进行了阐述和定义。通过联立误差状态空间模型和输出方程，求出状态转换矩阵，得到了误差敏感度的理论表达式。通过蒙特卡洛仿真的方法对上述敏感度的理论表达式进行了对比验证。研究表明，将动态系统灵敏度分析方法应用到多工位装配过程可行，基于状态空间模型的飞行器装配误差敏感度分析方法合理。