画图解题思路清

◎相 辉

在解决一些数学问题时，有些题目的数量关系会比较隐蔽或复杂，不易分析，这时如果能够借助画图，就可以把条件和问题直观地表示出来。这样不仅便于发现和分析数量之间的关系，还可清晰地探寻出解题思路。

一、平面图（关于图形与几何中的面积问题，可以画出平面图进行分析）

例1：丰收农牧渔场原来有一个长80米的长方形鱼池，后来因扩建公路，鱼池的长减少了5米，这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米？

分析与解：要求现在的面积，正常思路就是要知道现在长方形鱼池的长和宽分别是多少，因为它的宽是未知的，长又在变化，关系比较隐蔽。我们可以通过画图形的方法，把变化情况直观地表示出来。

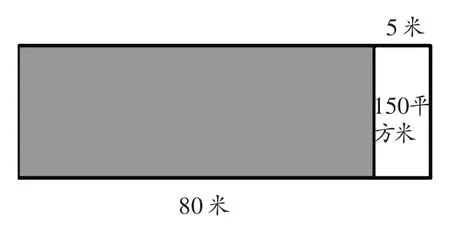
由上图可以直观地看出阴影部分的面积是现在长方形鱼池的面积，空白部分的面积就是减少的150平方米，宽是5米，长就是150÷5=30（米），也就是现在长方形的宽是30米；而长则是80-5=75（米），那么现在长方形鱼池的面积就是75×30=2250（平方米）。

二、线段图

例2：小明和小红共有260枚邮票，小明比小红多了20枚，问他们两人各有多少枚邮票？

分析与解：知道两人邮票数量的和与差，乍一看，无法解答，但只要画出线段图，就能很容易厘清思路，探寻出不同的方法。

从上图可以看出，给小红补上20枚，两人的数量就一样多，（260+20）是小明的2倍，小明的数量是（260+20）÷2=140（枚），小红的数量就是140-20=120（枚）；也可以把小明的邮票去掉20枚，使小明和小红一样多，（260-20）就是小红的2倍，因此小红的数量是（260-20）÷2=120（枚），小明就是260-120=140（枚）；如果小明给小红多出的一半20÷2=10（枚），则两人就一样多，但总数不变，先用260÷2=130（枚），小明的数量就是130+10=140（枚），小红就有130-10=120（枚）。

三、表格图

例3：小刚家栽了3行杨树、8行柏树和4行松树。杨树每行7棵，柏树每行6棵，松树每行5棵。杨树和松树一共多少棵？

分析与解：题目中的信息较多，如果能列表选择需要的条件进行整理，就能清楚明了地分析出数量关系，从而确定解答方法。

杨树3行每行7棵松树4行每行5棵

从表中可以看出，从条件想起，先分别算出杨树3×7=21（棵）和松树4×5=20（棵），最后求出杨树和松树一共21+20=41（棵）。