基于粗糙集与模糊理论的公路隧道塌方风险评价*

姜安民， 董彦辰， 张晓波， 熊奇伟， 李旋

(1.湖南城建职业技术学院, 湖南 湘潭 411100;2.中南林业科技大学 土木工程学院, 湖南 长沙 410004;3.湖南大学 土木工程学院, 湖南 长沙 410082)

公路隧道施工过程中塌方事故较为常见，是较严重的工程地质灾害之一。近年来，随着隧道工程建设的增多，塌方事故愈发频繁。隧道塌方严重影响工程的正常进度，威胁施工人员的生命安全并带来巨大经济损失。苏永华等通过隧道塌方事故统计，找出了地质因素、设计施工质量等六大塌方风险因素，引入重心理论计算客观权重，基于该权重给出了公路隧道塌方评估方法；关晓吉建立塌方风险等级评价因子体系，运用可拓联系云模型对隧道塌方风险等级进行了评价；杨卓等建立塌方风险评价指标体系，基于熵权物元可拓理论构建隧道塌方风险分级评估模型，并运用该模型进行了实例研究；秦胜伍等选取围岩级别、地下水状况等7个因素建立隧道塌方风险评价指标体系，基于最大熵原理和属性区间识别理论建立了山岭隧道塌方风险评价模型；孙彦峰选取岩石单轴饱和抗压强度等12个具有代表性的影响因素作为隧道塌方风险评价指标，建立基于理想点法的隧道塌方风险等级评价模型，并利用2个典型隧道样本对该模型进行了验证。该文借鉴前人研究成果，基于粗糙集与模糊理论对公路隧道塌方风险进行评价。

1 公路隧道塌方风险评价指标体系

导致公路隧道塌方的风险因素较多，从不同角度对风险因素进行划分会有所差异。如：陈建宏等将隧道塌方风险因素划分为静态孕险因子与动态致险因子两类，其中静态孕险因子包含围岩等级、隧道埋深等5项指标，动态致险因子包含大气降水、开挖跨度等4项指标；陈诚将隧道塌方风险因素划分为工程地质、水文气象、设计施工三类，其中工程地质包含岩石单轴饱和抗压强度、岩体完整性指数等5项指标，水文气象包含地下水渗水量、含水层透水性2项指标，设计施工包含隧道跨度、隧道埋深等3项指标。对隧道潜在风险因素进行梳理、归类，听取专家意见，结合评价对象的工程背景，重点参考文献[1]，建立表1所示公路隧道塌方风险评价指标体系，该评价指标体系包含3个一级评价指标、8个二级评价指标。

2 粗糙集理论及权重确定方法

2.1 粗糙集理论

粗糙集理论是研究知识与数据的数学理论和方法，主要用于不精确、不确定与不完整信息的分析处理，它主要是应用数据集自身的数据进行决策推理，问题所需处理的数据集合之外的信息不需提供，具有较强的客观性。

定义一个信息系统S，S可表达成一个有序四元组信息系统S=(U,A,V,f)，简记为S=(U,A)。其中：U为论域，是全体样本集合；A为属性集合，A=C∪D(C∩D=φ)；C为条件属性集合，反映对象特征；D为决策属性集合，反映对象类别；V为属性值集合，V=∪a∈AVa；f为信息函数，U×A→V，即对于∀x∈U，a∈U，有f(x,a)∈Va。

表1 公路隧道塌方风险评价指标体系

2.2 基于粗糙集理论的权重计算

在保持分类能力不变的情况下，删除冗余的条件属性，形成一个简化的决策表，此即为粗糙集属性简约的主要思想。条件属性的重要度高低决定决策属性所受影响程度的大小，二者呈正相关。冗余条件属性对决策属性的取值不产生影响，即属性重要度为零。权重确定步骤如下：

(1) 确定决策表。决策表S=(U,A),A=C∪D。

(2) 计算条件属性的重要度。计算D的C正域POSC(D),D对C的依赖度见式(1)。逐个去除条件属性{Ci}，按式(2)计算D的C-{Ci}正域和POSC-{Ci}(D)依赖度rC-{Ci}(D)。条件属性Ci的重要度ki按式(3)计算。

(1)

式中：|s|为集合s的元素个数。

(i=1,2,3,…,n)

(2)

ki=rC(D)-rC-{Ci}(D)

(3)

(4)

3 基于粗糙集与模糊理论的公路隧道塌方风险评价模型

3.1 模糊理论

自然界中存在很多模糊的概念或现象，而各学科都要求定量化、数字化，促使人们寻找一种研究处理模糊概念或现象的数学方法，模糊数学及相关理论应运而生。导致公路隧道塌方的风险因素较多，具有一定的模糊性与不确定性，故引入模糊理论构建公路隧道塌方风险评价模型。

3.2 公路隧道塌方风险评价

3.2.1 建立评价模型

通过文献研究和专家调查，基于粗糙集与模糊理论，构建图1所示公路隧道塌方风险评价模型。

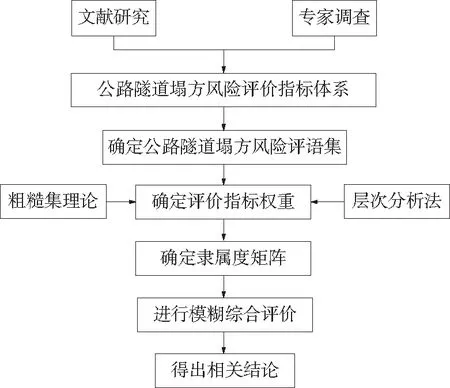
图1 公路隧道塌方风险评价模型

3.2.2 评价步骤

(1) 确定评价指标体系，即评价因素集合U={U1,U2,U3,…，Un}，其中U1={U11,U12,…，U1n}。如表1所示，公路隧道塌方风险评价指标体系包括3个一级评价指标、8个二级评价指标。

(2) 确定风险评价等级，即因素评语集合V={v1,v2,v3,…，vn}。将公路隧道塌方风险划分为5个等级(见表2)。

表2 公路隧道塌方风险等级划分

(5)

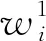
(4) 确定隶属度矩阵。采用定量法确定隶属度矩阵，该方法采用线性分析法，主要通过构造隶属度函数计算指标隶属度。构造图2所示梯形隶属度函数，其中a、b、c、d表示每个指标的阈值范围，x1～x8表示每个指标临近阈值的线性取值。公路隧道塌方风险分为v1、v2、v3、v4、v55个等级，各级隶属度函数分别见式(6)～(10)。根据隶属度函数计算各评价指标对风险等级的隶属度rij，形成隶属度矩阵[见式(11)]。

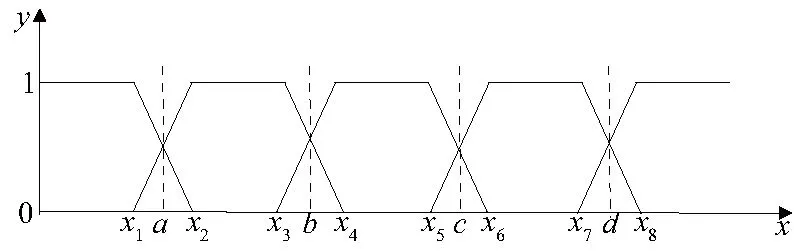
图2 梯形隶属度函数

(6)

(7)

(8)

(9)

(10)

(11)

(5) 进行模糊综合评价。按式(12)计算综合评价结果，根据最大隶属度原则确定公路隧道塌方风险所处等级，并给出合理建议。

B=W∘R=(b1,b2,b3,…,bn)

(12)

4 工程算例

4.1 工程概况

A市拟建某分离式公路隧道，左线起迄桩号ZK28+126—ZK29+145，长1 019m，最大埋深约145 m；右线起迄桩号K28+134—K29+142，长1 008m，最大埋深约150 m。隧道进口采用端墙式，出口采用削竹式。净宽10.45 m，净高5 m。围岩级别为Ⅴ级，节理裂隙发育，地下水较丰富，施工技术水平及管理水平较高。

4.2 隧道塌方风险评价

评价指标体系见表1，风险评价等级划分见表2。

(1) 确定评级指标权重。按式(5)计算，得各级评价指标权重Wi如下：

W=(0.220 1,0.679 9,0.100 0)

W1=(0.454 5,0.545 5)

W2=(0.397 1,0.308 8,0.191 2,0.102 9)

W3=(0.5000 0,0.500 0)

(2) 确定隶属度矩阵。邀请10位对该工程较熟悉的专家，根据风险量大小，对各项指标进行初始评分，分值取0～10。对所有评分加权平均确定综合评分，评分结果见表3。将梯形隶属度函数中x1,x2,x3,…,x8分别赋值1,2,3,…8，将表3中各指标评分结果代入式(6)～(10)，得评价指标的隶属度矩阵如下：

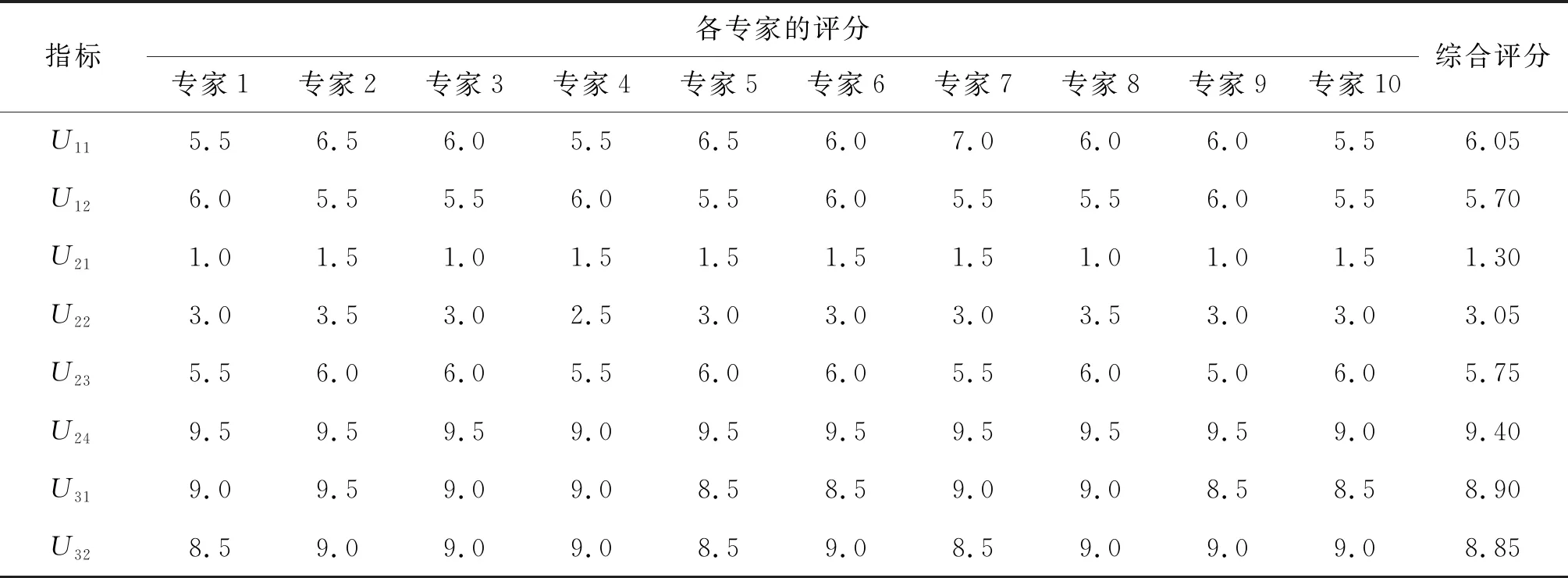
表3 风险评价指标综合评分

(3) 进行模糊综合评价。1) 一级模糊综合评价。按式(12)计算，得一级模糊综合评价结果分别见式(13)～(15)。 根据最大隶属度原则，勘察设计风险所处等级为v4级，风险较低；地质条件风险所处等级为v2级，风险较高；施工风险所处等级为v5级，风险低。2) 二级模糊综合评价。按式(12)计算，得二级模糊综合评价结果见式(16)。根据最大隶属度原则，公路隧道塌方总体风险所处等级为v4级，风险较低。

B1=W1∘R1=(0.454 5,0.545 5)∘

(0.000 0,0.000 0,0.163 7,0.836 3,0.000 0)

(13)

B2=W2∘R2=(0.397 1,0.308 8,0.191 2,0.102 9)∘

(0.278 0,0412 5,0.063 2,0.143 4,0.102 9)

(14)

B3=W3∘R3=(0.500 0,0.500 0)∘

(0.000 0,0.000 0,0.000 0,0.000 0,1.000 0)

(15)

B=W∘R=(0.220 1,0.679 9,0.100 0)∘

(0.189 0,0.280 5,0.079 0,0.281 6,0.170 0)

(16)

5 结论与建议

通过查阅相关文献资料，并听取专家意见，结合评价工程的实际情况建立公路隧道塌方风险评价指标体系，该评价指标体系包含勘察设计风险、地质条件风险等3个一级评价指标，地质勘察风险、开挖跨度风险等8个二级评价指标。基于粗糙集理论确定评价指标客观权重，同时运用层次分析法对客观权重进行修正，充分考虑决策者的阅历、经验，使权重分配更合理。运用该评价模型对某拟建公路隧道塌方风险进行评价，得出一级指标勘察设计风险、地质条件风险、施工风险所处风险等级分别为v4、v2、v5级，即风险较低、风险较高、风险低，隧道塌方总体风险为v4级，风险较低。虽然总体风险处于较低状态，但一级指标中地质条件风险较高。该工程围岩级别为Ⅴ级，节理裂隙发育，地下水较丰富，建议提前采取相应措施加以应对。