波形钢腹板预弯组合梁承载性能影响因素分析*

2020-07-06徐文豪贺君陈卓异李传习李向

公路与汽运 2020年3期

徐文豪，贺君，陈卓异，李传习，李向

(长沙理工大学桥梁工程安全控制教育部重点实验室，湖南长沙 410114)

预弯组合梁为砼顶、底板与预弯钢梁构成的钢混组合结构，具有结构刚度大、建筑高度低、自重轻、施工速度快及外形美观等优点。该结构先将钢梁预压，压平后浇筑底板砼，再利用钢梁反弹为底板砼施加预压应力，无需布设预应力筋。国内外学者如Maeda Yukio、Asakawa Kazuo、Doobyong Bae、黄侨、邢力、郭赵元、李喆等对传统预弯静力与疲劳性能、动力性能、设计理论等进行了较全面的试验研究，这些研究主要针对传统预弯工字钢梁，其腹板为平钢腹板，横向刚度小，在钢梁预压阶段易发生腹板屈曲，故需在腹板上焊接额外的加劲肋。此外，由于平钢腹板限制了砼的收缩和徐变作用，引起下翼缘砼应力重分布，将导致较大的预应力损失。

与平钢腹板相比，波形钢腹板可提供较强的面外刚度且无需设置加劲肋。同时波形钢腹板的手风琴效应能减少砼收缩徐变产生的应力重分布，因而能很好地将预压应力施加于下翼缘砼。波形钢腹板预弯组合梁充分利用波形钢腹板轴向刚度小及预弯梁反弹后砼底板形成预压应力的特点，具有建筑高度低、无需预应力筋、预应力损失小等优点。陈卓异等对波形钢腹板预弯梁组合结构的制作工艺与承载性能进行研究，验证了其优异的受力性能。但目前对预弯组合梁力学性能参数的分析较少。该文通过波形钢腹板预弯梁模型试验与有限元分析，研究预弯波形腹板钢梁高度、翼缘板宽度、腹板厚度及腹板波高等参数对结构承载性能的影响，探究预弯组合梁预压阶段钢梁稳定性与极限状态承载性能，为波形钢腹板预弯组合梁设计提供参考。

1 模型试验

试验梁全长6 500 mm，其细部尺寸构造见图1。预弯钢梁上下翼缘板和波形钢腹板均选用Q345钢，上下翼缘板外侧布置直径13 mm、间距150 mm的焊钉。其中：率先浇筑的底板砼为一期砼，选用C50砼，同时布置5根φ12 mm受拉钢筋；待钢梁回弹完成后浇筑的顶板砼为二期砼，选用C40砼，并布置4根φ12 mm受压钢筋。箍筋直径8 mm，间距100 mm。采用50 t液压千斤顶对试验梁进行两点对称加载(见图2)，两加载点分别距跨中900 mm。

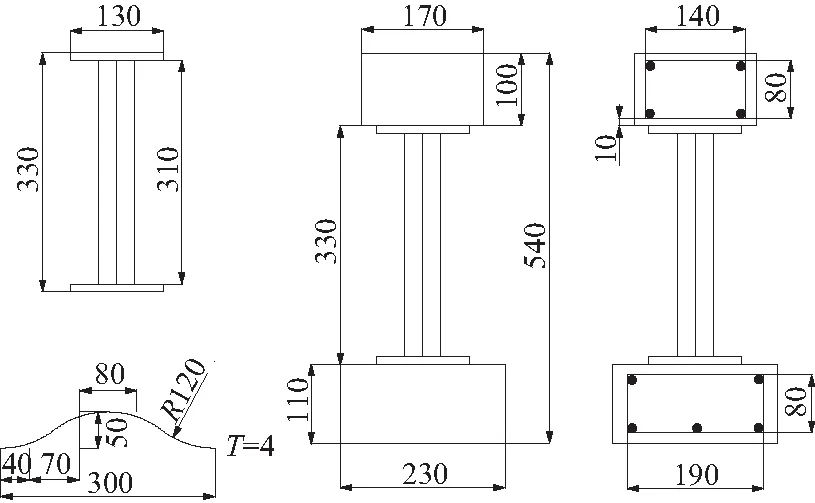
图1 波形钢腹板预弯梁的构造(单位：mm)

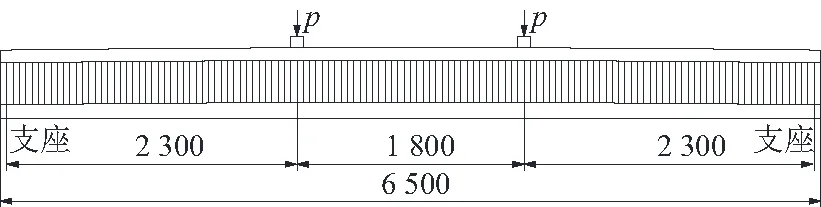
图2 波形钢腹板预弯梁试验加载示意图(单位：mm)

2 有限元建模

2.1 模型建立

利用通用有限元软件ABAQUS(V2018)模拟试验梁预压、反弹及加载过程，有限元模型见图3。波形钢腹板预弯钢梁采用减缩积分壳单元、砼顶底板采用三维八节点非协调实体单元、钢筋采用两结点线性三维桁架单元模拟，有限元模型总体单元划分规则、均匀。钢筋与砼之间的作用采用ABAQUS的内置区域约束(embedded region constraints)，上下翼缘钢板与顶底板砼通过绑定约束(tie constraints)模拟焊钉连接件作用，同时通过约束钢梁上翼缘板两侧面的横向自由度模拟试验中的侧向支撑。试验梁两端简支，并在加载位置处施加竖向位移荷载。整个钢梁预压、浇筑砼顶底板及最终加载过程通过相互作用(interaction)模块里的模型改变(model change)即单元生死的原理实现。

图3 波形钢腹板预弯梁有限元模型

2.2 材料本构

有限元模型中钢板与钢筋均采用强化的双折线模型，折线第一上升段斜率为钢材本身弹性模量，第二上升段为强化段，斜率大致取为第一段的1%。砼采用塑性损伤模型，其单轴拉伸与单轴压缩本构关系见图4。

在砼单轴拉伸或压缩时，应力应变关系在σt0、σc0之前为线弹性，超过极限应力后应力应变曲线进入软化段，此时材料应力应变关系可表示为：

(1)

采用GB 50010-2002《混凝土结构设计规范》提供的弹性模量与泊松比，根据规范中附录C2提供的砼单轴应力应变关系曲线进行计算，获得σc、εc及σt、εt。损伤因子采用张劲公式计算：

dk=(1-β)εinE0/[σk+(1-β)εinE0] (k=t,c)

(2)

式中：β为塑性应变与非弹性应变的比例系数，受压时取0.35～0.7，受拉时取0.5～0.95；εin为砼拉压情况下的非弹性应变。

根据以往研究，建议β受压时取0.6，受拉时取0.9。最后通过式(3)得到ABAQUS所需开裂应变

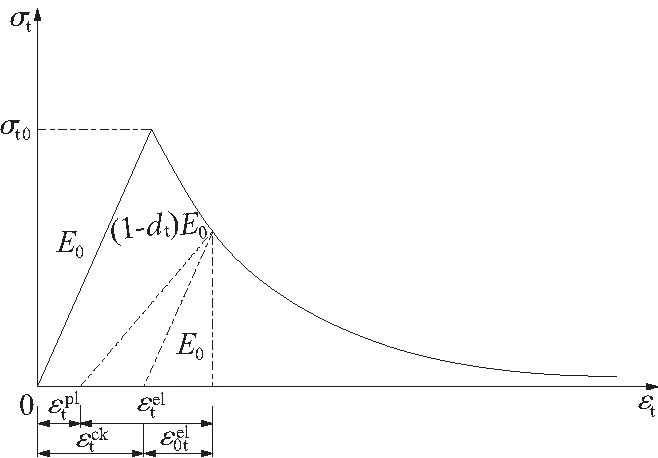
(a) 单轴拉伸

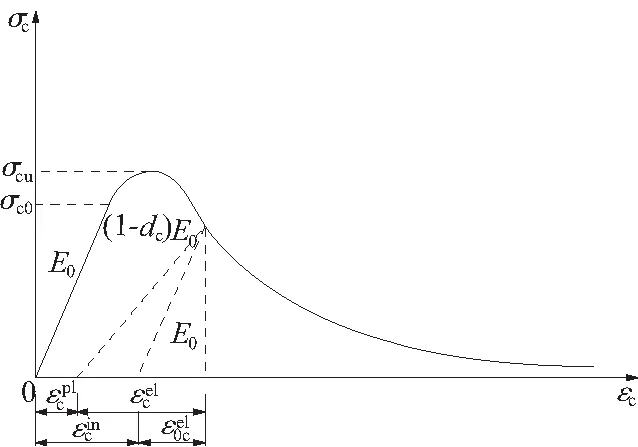
(b) 单轴压缩

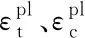
图4 单轴拉伸与单轴压缩本构关系

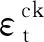
(3)

3 试验与有限元结果分析

3.1 钢梁反弹后砼底板预压应力

波形钢腹板钢梁在预弯荷载96 kN作用下浇筑一期砼，钢梁反弹时对砼底板施加预压力，跨中和四分点处的预压应力对比见图5。跨中砼下缘最大压应力实测值与模拟值分别为12.9，12.03 MPa，最大误差为7%，有限元模型能较好地模拟预压阶段的结构响应，且波形钢腹板预弯钢梁反弹能有效地将预压应力施加于砼底板上。

3.2 加载阶段荷载-挠度关系

试验梁荷载-挠度曲线对比见图6。曲线大致分为线弹性、弹塑性及塑性3个阶段，实测曲线与模拟曲线的趋势基本一致。实测极限承载力为127.3 kN，模拟值为128.4 kN，误差仅0.86%。有限元模型可精确地模拟加载全过程试验梁的强度与刚度。

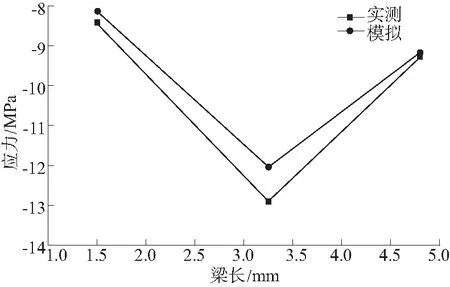
图5 一期砼下缘预压应力对比

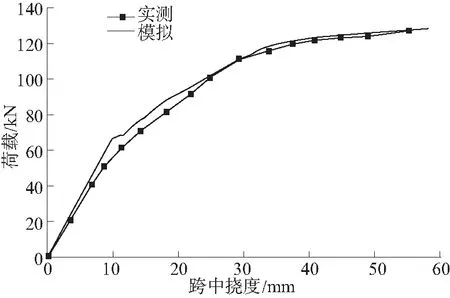
图6 预弯梁荷载-挠度对比

3.3 破坏模式

试验梁最终破坏模式为顶板砼两加载点之间及附近局部压溃，同时出现纵向裂纹(见图7)，在破坏过程中，试验梁显示出良好的延性。有限元模拟的破坏模式见图8，顶板砼加载点附近及中间局部出现受压损伤因子超过0.3，砼已压碎，有限元模拟能有效预测试验梁的破坏形式及位置。

图7 顶板砼局部压溃及纵向裂纹

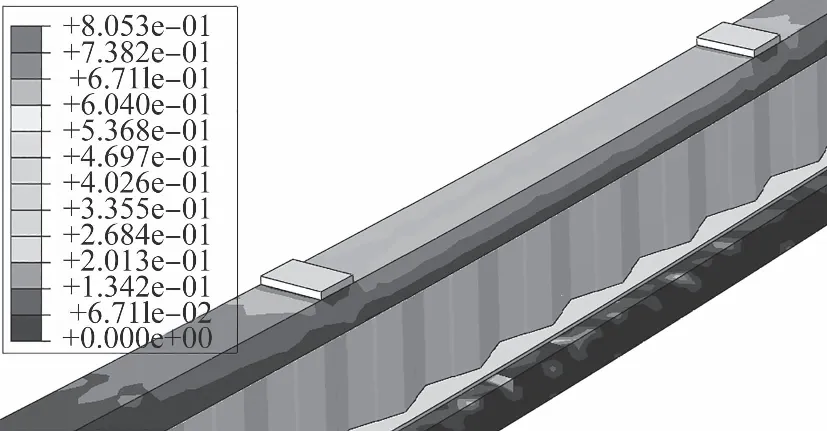
图8 有限元模拟顶板局部受压损伤破坏

4 承载性能影响因素分析

4.1 钢梁梁高的影响

原模型中预弯钢梁高330 mm。为更好地进行对比研究，将预弯钢梁高变化为270、300、360、390 mm，通过有限元模型计算得到预弯钢梁反弹后砼底板应力和组合梁的极限承载力(见图9)。

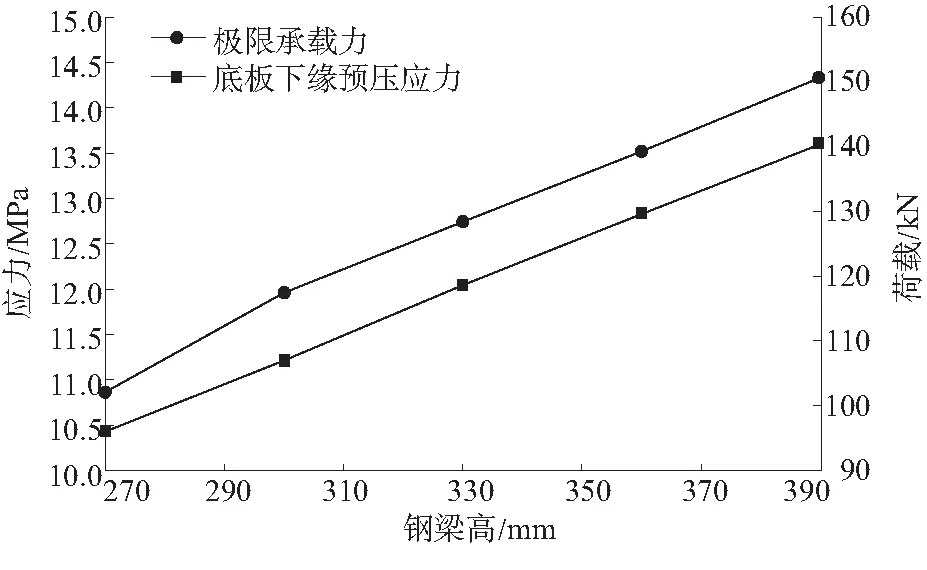
图9 不同钢梁高对应的预压应力和极限承载力

由图9可知：钢梁高为270、300、360、390 mm时，跨中底板砼下缘预压应力最大值分别为10.42、11.22、12.83、13.6 MPa，预弯组合梁极限承载力分别为102、117.4、139.2、150.7 kN，相比梁高330 mm的预弯梁，预压应力分别变化-13.3%、-6.7%、6.6%、13%，极限承载力分别变化-20.5%、-8.5%、8.4%、17.3%。表明砼底板预压应力和预弯组合梁极限承载力受梁高影响显著，且随着梁高的增大线性增加。

4.2 翼缘板宽度的影响

原模型中预弯钢梁的翼缘板宽度为130 mm。为更好地进行对比研究，将预弯钢梁翼缘板宽变化为90、110、150、170 mm,通过有限元模型计算得到预弯钢梁反弹后砼底板应力和组合梁的极限承载力(见图10)。

由图10可知：钢梁翼缘板宽度为90、110、150、170 mm时，跨中底板下缘砼预压应力最大值分别为10.32、11.15、12.81、14.22 MPa，预弯组合梁极限承载力分别为99.8、117.7、137.5、152.1 kN，相比翼缘板宽度130 mm，预压应力分别变化-14.2%、-7.8%、6.4%、18.2%，极限承载力分别变化-22.2%、-8.3%、7%、18.4%。由于钢梁中的波形钢腹板主要承担剪切力，对抗弯贡献小，钢梁上下翼缘板为主要抗弯构件，预弯梁预压应力和极限承载力受翼缘板宽度影响大，且随着翼缘板宽度的增大几乎线性增加。

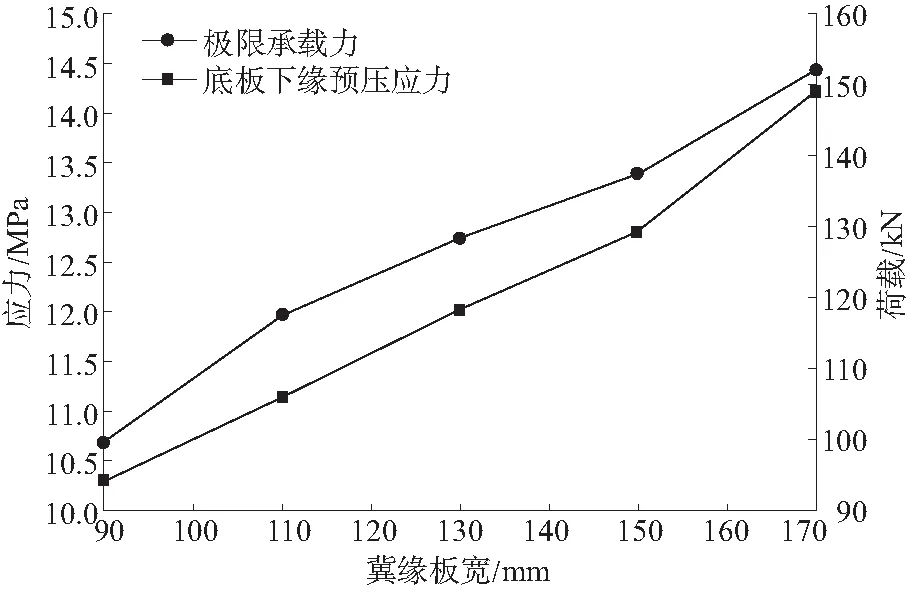
图10 不同钢梁翼缘板宽对应的预压应力和极限承载力

4.3 腹板厚度的影响

原模型中预弯钢梁腹板厚度为4 mm。为更好地进行对比研究，将预弯钢梁腹板厚变化为2、3、5、6 mm,通过有限元模型计算得到预弯钢梁反弹后砼底板应力和组合梁的极限承载力(见图11)。

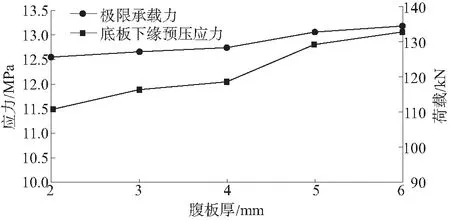
图11 不同钢梁腹板厚度对应的预压应力和极限承载力

由图11可知：腹板厚度为2、3、5、6 mm时,跨中底板下缘砼预压力最大值分别为11.47、11.87、12.79、13.05 MPa，预弯组合梁极限承载力分别为125.6、127.1、132.7、134.4 kN，相比腹板厚4 mm，预压应力分别变化-4.6%、-1.3%、6.3%、8.4%，极限承载力分别变化-1%、-3.3%、2.1%、4.6%，预压应力与极限承载力均随腹板厚度增大而缓慢增加。但与钢梁高和翼缘板宽带来的变化相比，腹板厚度变化的影响较小。

4.4 波形腹板波高的影响

原模型中预弯钢梁腹板波高为50 mm，平钢板与斜钢板之间的圆角半径为120 mm。为保证圆角半径一致，分析时仅变化波高这一参数，分别取30、35、40、45、51 mm，通过有限元模型计算得到预弯钢梁反弹后砼底板应力和组合梁的极限承载力(见图12)。

由图12可知：波形腹板波高为30、35、40、45、51 mm时，跨中底板下缘砼预压力最大值分别为12.1、12.02、12.08、12.06和12.01 MPa，预弯组合梁极限承载力分别为120.4、120.5、121.4、123.5、129.4 kN，相比波高50 mm，预压应力分别变化0.5%、-0.08%、0.4%、0.2%、-0.16%，极限承载力分别变化-6.2%、-6.1%、-5.4%、-3.8%、0.7%，预压应力基本保持不变，极限承载力随波高增大缓慢增加。但与钢梁梁高和翼缘板宽带来的变化相比，腹板波高的影响也较小。

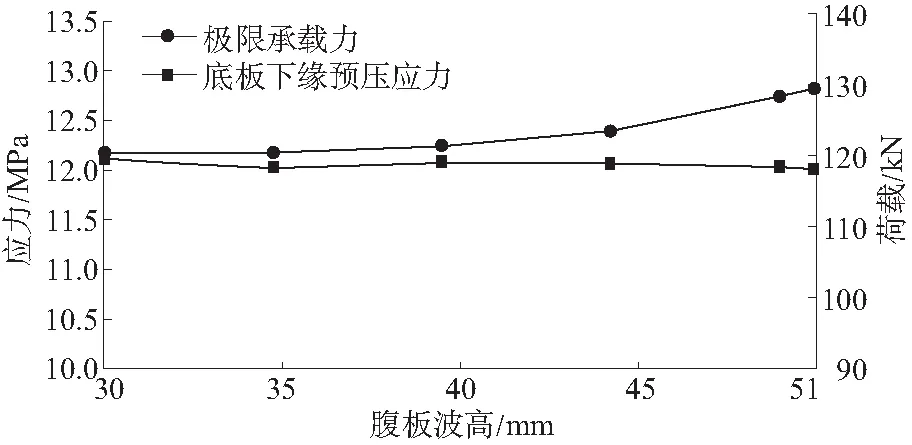
图12 不同钢梁腹板波高对应的预压应力和极限承载力

5 稳定性影响因素分析

由于预弯波形腹板钢梁长细比较小，且预弯阶段承受预压荷载，若无足够的侧向支撑，易发生整体侧倾失稳。为研究预压阶段波形腹板钢梁的稳定性，以试验波形腹板钢梁为基本模型，通过改变结构参数，对波形腹板钢梁预压工况进行线性屈曲分析，获得屈曲(失稳)荷载(见图13)。

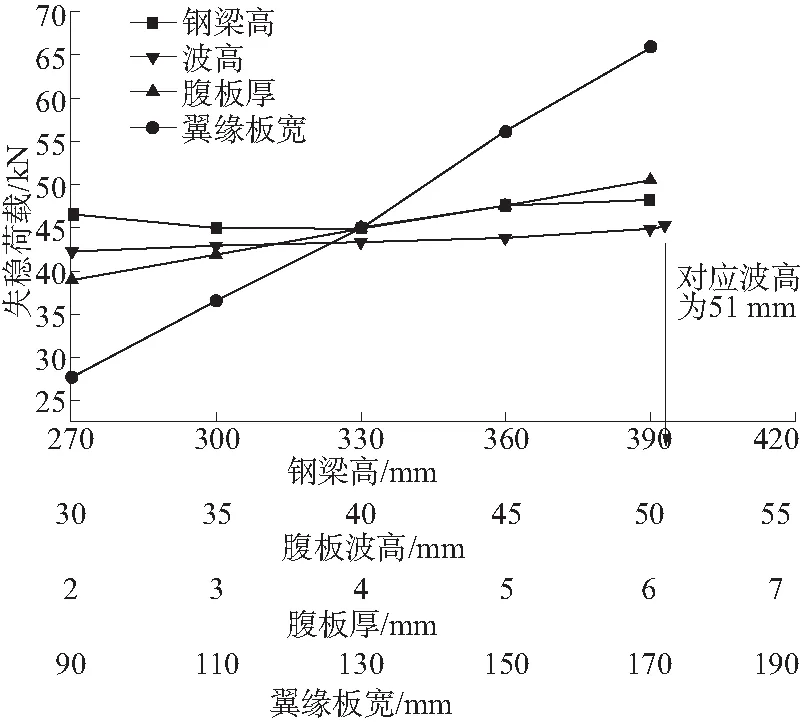
图13 各影响因素下预弯钢梁的失稳荷载

由图13可知：1) 在预弯力作用下，钢梁发生相同转角时，梁高越大，上翼缘离开梁纵轴线的水平位移越大，更易发生侧倾失稳。但梁高的增大也在一定程度上增大了抗弯模量。综合两方面影响，预弯钢梁预压失稳荷载变化规律表现为先小幅减小后小幅增大。2) 预弯钢梁预压阶段失稳荷载受翼缘板宽度影响显著，失稳荷载随翼缘板宽度增大基本呈线性增长。3) 腹板厚度与腹板波高的增加都会引起预弯钢梁预压失稳荷载小幅增加，但与翼缘板宽度的影响相比变化幅度很小。综合分析，预弯钢梁失稳荷载受翼缘板宽度影响最显著。此外，参数分析中所有钢梁的失稳荷载均小于试验预弯荷载96 kN，预压过程中需做好足够的预防失稳措施，保证预压阶段钢梁不发生屈曲失稳。