UGM(1，1)模型在特殊路基沉降中的应用

刘跃

(湖南省高速公路集团有限公司 湘西分公司， 湖南 长沙 410003)

某高速公路K4+860—K9+960段地貌以丘陵为主，路线穿越山岭、田野和山谷，地形起伏较大。所处位置地质构造简单，岩层均为单斜构造，孔隙水量较小，主要赋存在小部分卵石和块石中。为提高施工的经济性，填筑材料选自附近山体边坡，主要由红砂岩碎石土构成，其占比超过70%。红砂岩在环境因素影响下将产生强度降低现象，导致红砂岩碎石土路基的施工质量较难控制，路基在荷载作用下会出现大规模不均匀沉降。因此，该路段路基施工中采用强夯法进行加固处理。该文通过拉格朗日插值函数将原始非等时距时间序列转化为等时距时间序列，建立UGM(1，1)模型预测路基沉降，研究红砂岩碎石土强夯路基的沉降特性及改善情况。

1 GM(1,1)模型简介

灰色GM模型具有随机性、模糊性、不确定性，可揭示内部结构的连续变化，在路基沉降中应用十分普遍。典型灰色模型GM(1,1)的建模过程如下：

从测量的累积沉降数据中提取一系列相等时间间距的数据作为原始数据序列：

S(0)=[S(0)(1),S(0)(2),…,S(0)(n)]

累加原始数据序列一次，得到一个新的时间序列：

S(1)=[S(1)(1),S(1)(2),…,S(1)(n)]

令Z(1)=[z(1)(2),z(1)(3),…,z(1)(n)]，则GM(1,1)模型的基本方程为：

S(0)(k)+az(1)(k)=b

其白化方程为：

系数a、b采用最小二乘法计算。时间响应函数为：

从而得到：

使S(1)(0)=S(0)(1)，有：

则：

2 非等时距GM(1，1)模型

受施工环境、天气变化及人为因素的影响，红砂岩碎石土路基沉降数据序列的时间间隔并非等距，导致GM(1，1)模型的运用存在一定局限性。为准确掌握红砂岩路基的沉降规律，建立基于GM(1，1)模型的UGM(1，1)预测模型，其建立过程类似于等时距序列模型。

2.1 非等时距序列转换成等时距序列

非等时距沉降增量时间序列为：

S1(1)={S1(0)(ti)|i∈R+，i=1，2，…，n}

各时段的时间间隔为：

Δti=ti+1-ti；Δtj=tj+1-tj

式中：Δti-Δtj≠0；i≠j，i，j∈{1，2，…，n-1}，表示各时段的时间间隔不相等。

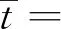
t=n时：

t=2，3，…，n-1时，使用拉格朗日插值函数对线形进行分段内插处理，得：

等时距沉降增量时间序列为：

这样，非等时距序列转换成了等时距序列。再根据等时距序列求得时间响应函数：

2.2 模型的精度检验

常用模型精度检验方法有残差检验法、关联度检验法和后验差检验法。采用后验差检验法对UGM(1，1)模型的预估值进行验证。该方法采用后差分比C和小误差概率P描述模型精度[见式(1)]，精度等级评定标准见表1。

(1)

表1 模型精度等级评定标准

根据表1及式(1)，外推性好的预估，C值越小，P值越大，所得沉降数据的离散程度越大，且残差与残差均值的差值符合要求的点越多，模型预估值的精度越好。

3 实例分析

为测试UGM(1，1)模型在路基沉降预测中的可靠性，以该工程K4+920断面中线位置沉降点的沉降观测数据为原始对比值。K4+920断面位于池塘上方，路基结构受到淤泥层的影响。在建造路基之前，先清理表面污泥、填充并压实。路基施工高度12.6 m，填筑材料为红砂岩。为控制路基施工质量，红砂岩粒径控制在34 mm。该断面于2017年2月埋设沉降板，强夯加固于2017年9月结束，沉降观测周期为17个月。

3.1 现场实测沉降

由于红砂岩碎石土路基是一种典型的渗透性较大的路基，在水的作用下易发生崩解，导致颗粒间的孔隙水加速流失，并且路基在强夯作用下沉降突变现象明显。为消除沉降突变因素对模型精度的影响，在确定基础数据之前适当剔除沉降突变数据。图1为K4+920断面沉降板的累计沉降。

图1 K4+920断面累计沉降-时间曲线

由图1可知：K4+920断面作为强夯路基截面，其累计沉降-时间曲线整体上较曲折，突变现象明显，最高突变量达50 mm。在原始数据的选择上应尽量避免沉降突变的时间段。

3.2 精度检验分析

3.2.1 模型建立

选择K4+920截面强夯后中央沉降板186～367 d的沉降观测数据作为基础建模数据，剔除沉降突变数据后建立UGM(1，1)预估模型。建模过程如下：1) 计算沉降过程平均时间间隔，得t=11.53 d；2) 根据拉格朗日插值定理确定等时间间距的沉降量；3) 根据灰色理论GM(1，1)模型的最小二乘法计算模型参数，得a=0.085 8，b=29.737 8；4) 将a、b参数值和实际沉降观测记录中的时间序列代入时间响应函数，得到该观测点的UGM(1，1)预估模型[见式(2)]。

S(t)=-125.994 4e-0.007 4(t-186)+346.594 4

(2)

3.2.2 模型精度检验

通过后验差检验法对式(2)的精度进行检验，得C=0.239 5，P=1，该UGM(1，1)预估模型精度好，不必通过残差模型进行校正。

3.2.3 模型拟合值和实测值对比

将观测点的模型拟合值和实测沉降值进行比较，结果见表2、图2、图3。

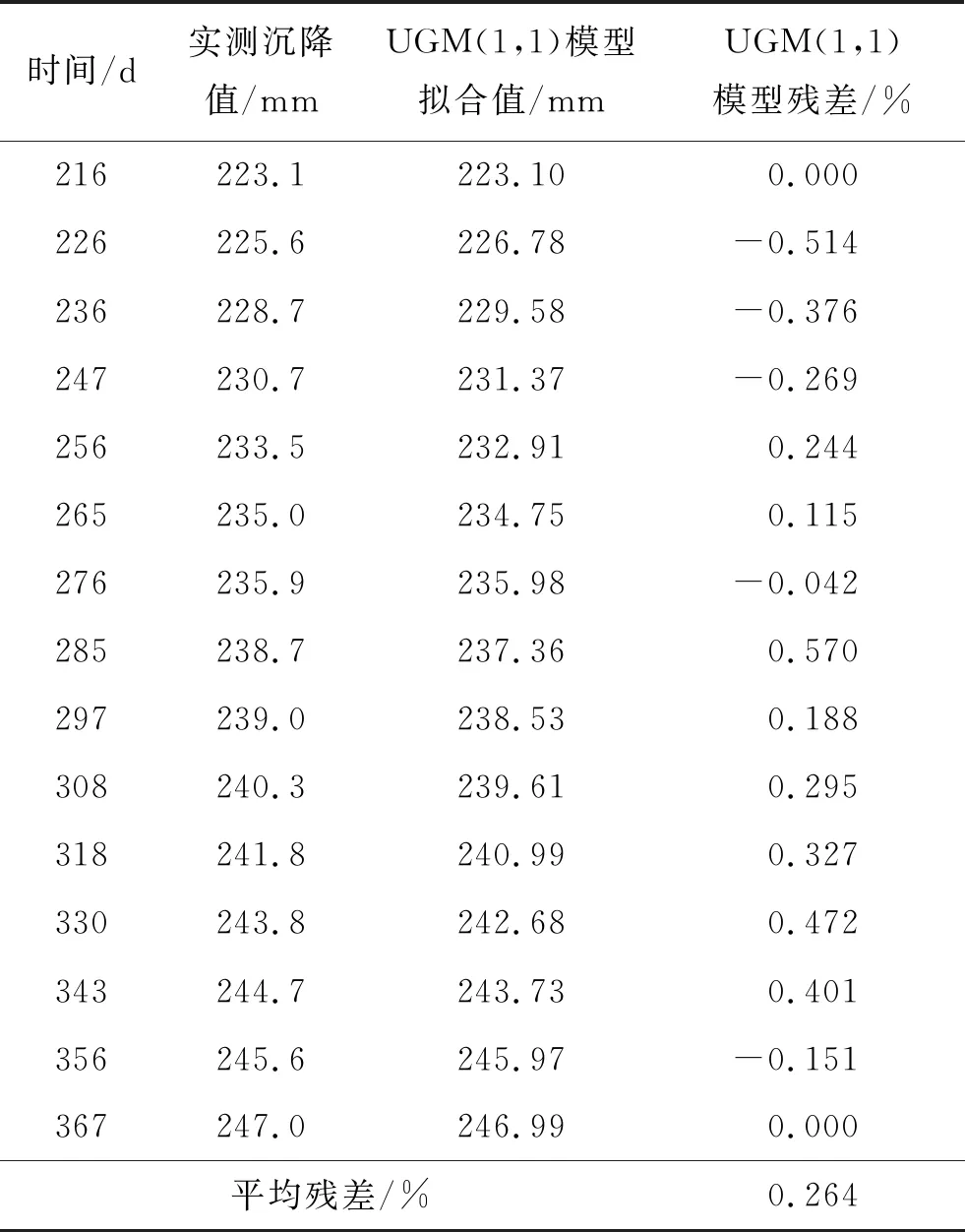
表2 UGM(1，1)模型拟合值和实测沉降值对比

图2 UGM(1，1)模型沉降拟合曲线与实测沉降曲线对比

由表2、图2、图3可知：UGM(1，1)模型拟合值和实际沉降值的平均残差为0.264%，最高残差为226 d的-0.514%，最低残差为367 d的零，模型拟合值很贴近实际沉降值。

图3 UGM(1，1)模型拟合误差

3.2.4 模型预估值和实测值对比

利用UGM(1，1)模型分别预测391和424 d的沉降，并与实测沉降进行对比，结果见表3。

表3 UGM(1，1)模型预估值与实测沉降值对比

由表4可知：UGM(1，1)模型对391 d的预估值与实际累计沉降值的误差为-0.088%,424 d预估值的误差为0.079%，该模型对红砂岩碎石土强夯路基沉降的预测精度较高。

4 结语

建立非等时距UGM(1，1)模型对某高速公路K4+860—K9+960路段红砂岩碎石土强夯路基沉降进行预测，得出如下结论：1) UGM(1，1)模型的拟合曲线和实际沉降曲线拟合程度较高，可利用该模型预测红砂岩碎石土强夯路基的沉降；2) UGM(1，1)模型预测值和实际沉降值的误差很小，对红砂岩碎石土强夯路基沉降的预测精度较高，适用于强夯路基沉降预测且具有较高的可靠性。但该模型对其他类型路基沉降的应用情况还需进一步研究。