路面结构数值计算尺度效应分析*

谢波， 张健

(长沙理工大学 交通运输工程学院， 湖南 长沙 410114)

合理、准确地分析沥青砼路面结构的力学响应规律，往往需借助设置合理有效的力学模型。通常采用有限元法计算分析行车荷载作用下沥青路面响应规律，采用的是有限结构模型，与沥青路面的假设即半空间无限体存在误差。因此，存在模型尺度合理选择问题。若尺度过小，会导致数值分析结果失真；若尺度过大，会增加计算分析的工作量，影响计算分析速度。

任俊达等建立基于实测参数的典型半刚性基层沥青路面三维粘弹有限元仿真模型，该模型在长度、宽度和深度方向的尺度分别为8、4、5 m，分析路面结构在不同加载位置下的力学响应和路面结构内部的力学响应规律。张丽娟等根据旧路及拟定加铺层结构形式确定模型尺度，其中每块板的尺度为5 m×3.75 m×0.26 m，C20水泥砼底基层的尺度为10.008 m×3.75 m×0.2 m，地基扩大尺度取12.008 m×4.75 m×9 m，通过预埋温度传感器实测路面温度场,根据传热学原理建立了旧水泥路面加铺沥青层结构的非线性瞬态3D温度场计算模型。任瑞波等建立纵向、横向及竖向尺度分别为14、6.3、3.14 m的有限元模型，分析移动荷载作用下饱和沥青路面的动力响应。陆辉等建立尺度为x=2.2 m、y=2.0 m、z=5.0m的模型，进行轮载作用下沥青路面三维非线性有限元分析。董轶等利用尺度为x=3.75 m、y=6.0 m、z=3.5 m的模型，利用三维非线性有限元分析了沥青路面车辙问题。Niki D.Beskou等开展移动车辆下3-D柔性路面动态弹性与非弹性分析，有限元模型在垂直、横向、纵向的尺度分别为29.45、15.00、30.00 m。Reaz Imaninasab等考虑半轮载荷下长度为1.3 m、宽度为1.5 m、深度为3.02 m的路面块，采用有限元方法分析了橡胶多孔沥青的车辙性能。不同学者在分析沥青路面时所采用的三维结构尺度五花八门，精确确定结构尺度势在必行。该文采用轴对称模型对路面进行分析，利用沥青路面多层弹性层状体系理论研究沥青路面结构有限元模型，计算确定特定沥青路面结构在不同误差下的精确尺度，为工程实践问题分析提供参考与帮助。

1 土基弯沉效应数值分析

面层、基层、垫层和路基材料为线弹性材料，应力应变关系符合广义虎克定律；平面方向每个层面无限大，且最远处的应力和位移分量为零；垂直方向有一定厚度，在无限远处和无限深处应力、位移都为零；行车荷载作用下路面表面产生的荷载是对称的。

根据JTG D50-2017《公路沥青路面设计规范》，路面结构设计采用双圆垂直均布荷载作用下的多层弹性层状体系理论进行计算，路面设计采用双轮组单轴载100 kN作为标准轴载，以BZZ-100表示。考虑到荷载与路面结构的对称性，采用轴对称结构对路面进行分析，并将单轮传压面当量圆直径取为20 cm。计算荷载(JZZ-100)与JTG D50-2017中标准轴载(BZZ-100)的对应关系见表1。

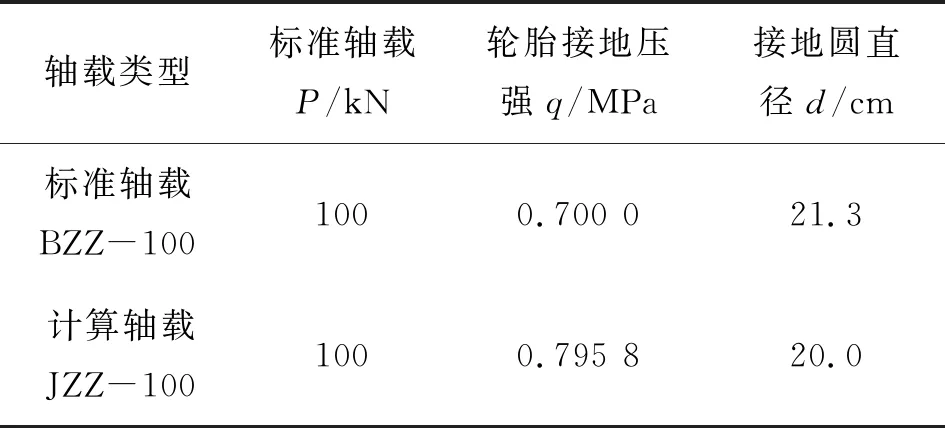
表1 轴载计算参数

提出表1所示换算关系，一是考虑到数值实施上的便利性，二是基于设计计算的合理性。此外，这种转换也是符合实际情况的，如载重货车中广泛使用的11.00-20轮胎，其胎冠宽度的实测值更接近20 cm，而BZZ-100将单轮传压面当量圆直径d取为21.3 cm，可能是为了取得一个包含较少有效数字的轮胎接地压强(0.7 MPa)而做的简单处理。这里先考虑荷载直接作用在土基上，根据JTG D50-2017，土基弹性模量取80 MPa，泊松比为0.4，采用八节点四边形单元，结构尺度从1 m逐渐变化到20 m，采用轴对称结构(见图1)。

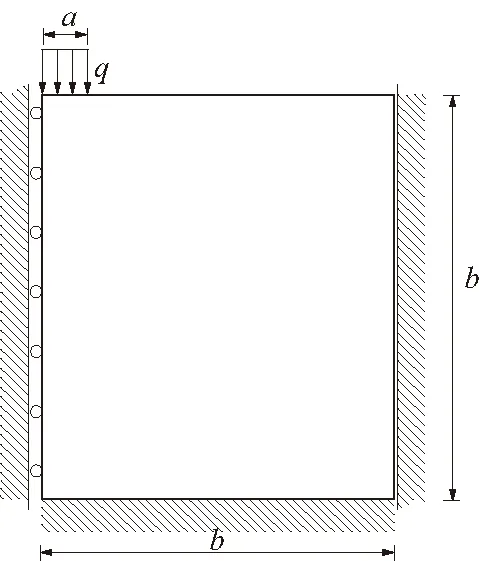
图1 荷载作用土基轴对称模型

半无限体圆形边界平面上，半径为a的圆内受到均匀压力q[见图2(a)]。如图2(b)所示，计算点M在圆内时，根据文献[1]，其竖向位移w见式(1)；点M在圆周上时，c=a，其竖向位移见式(2)；点M在圆心时，c=0，其竖向位移见式(3)。

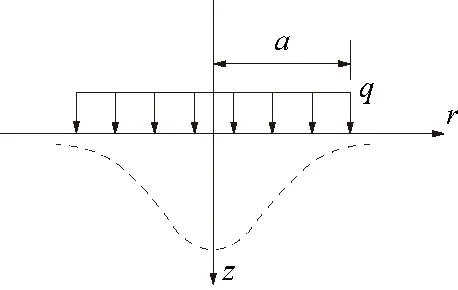
(a) 半无限体圆形界面受均匀压力

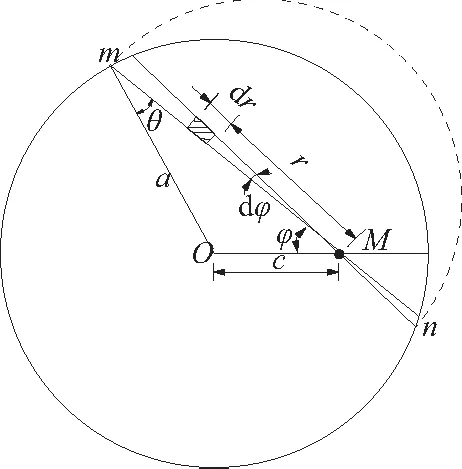
(b) 圆内点位移的积分

(1)

(2)

(3)

式中：ν为泊松比，取为0.4；q为计算荷载，其值为0.795 8 MPa；E为弹性模量，取为80 MPa；a取单轮传压面当量圆的一半，为0.1 m。

对比可见，圆心处位移最大，且位移随圆半径a增大而呈比列增大。根据式(3)计算的理论值为1.671 2×10-3m。网格大小分别取0.05、0.1、0.2 m，土基尺度a取为1～20 m，计算与理论值的误差，结果见图3。由图3可知：网格宽度分别为0.05和0.1 m时，误差曲线基本重合；而网格宽度为0.2 m时，与前二者误差较大，曲线发散。因此，有限元计算时设置网格宽度为0.05 m。

为确定最大误差为1%时土基结构尺度，采用拉格朗日插值法，得式(4)，每个拉格朗日基本多项式见式(5)。运用拉格朗日插值法得1.671 2×10-3×99%=l0(x)f(7)+l1(x)f(9)+l2(x)f(11)，x=8.7 m。结构尺度取土基尺度为8.7 m，有限元计算弯沉值与理论弯沉值的误差为1%，要保证数值计算与理论值误差在1%以内，结构尺度至少要大于8.7 m。

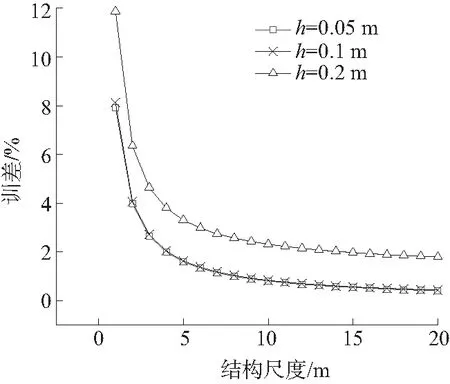
图3 不同结构尺度下的误差分析

(4)

(5)

同样取网格宽度为0.05 m，采用拉格朗日插值法，得式(6)，每个拉格朗日基本多项式见式(7)。运用拉格朗日插值法得1.671 2×10-3×95%=l0(x)f(1)+l1(x)f(2)+l2(x)f(3)，x=1.8 m。土基尺度为1.8 m，有限元计算弯沉值与理论弯沉值的误差为5%，要想数值计算与理论值的误差在5%以内，结构尺度至少要大于1.8 m。变化土基模量，结论一致，说明与假设的土基模量没有关系。

(6)

(7)

2 多层路面数值分析

选取一条典型路段，路面结构及材料参数见表2，为典型的半刚性沥青路面结构。

沥青面层采用20 ℃、10 Hz条件下的动态压缩模量，无机结合料稳定层采用经调整系数修正后的弹性模量。该文是研究多层沥青路面的精确尺度，虽然JTG D50-2017《公路沥青路面设计规范》取消了弯沉值这一传统指标，但考虑到弯沉是反映路面结构在荷载作用下整体结构承载能力大小的指标，与路面结构的各种病害形式和使用功能评价有一定关系，一味地追求弯沉指标或忽视弯沉指标对于路面结构设计都是不完善的，保留弯沉值这一传统控制指标。以JTG D50-2017为依据，从弯沉值、基层层底拉应力、底基层层底拉应力与反映沥青混合料永久变形量的竖向压应力4个指标进行分析。由于多层沥青路面的弯沉理论值公式极其复杂，采用路面结构尺度为50 m×50 m的计算值作为弯沉理论值，通过结构层的尺度变化与50 m×50 m作比较[见式(8)]，得出误差分别为1%与5%的结构尺度。同时考虑到设计中通常通过调整基层厚度来设计路面结构，主要分析基层厚度与基层模量变化对结构尺度的影响。用基层层底拉应力、底基层层底拉应力和竖向压应力作为控制指标采取的方法与以弯沉值为控制指标的方法一样。图4为高速公路、一级公路常见沥青路面结构，图5为各控制指标的误差分析结果。

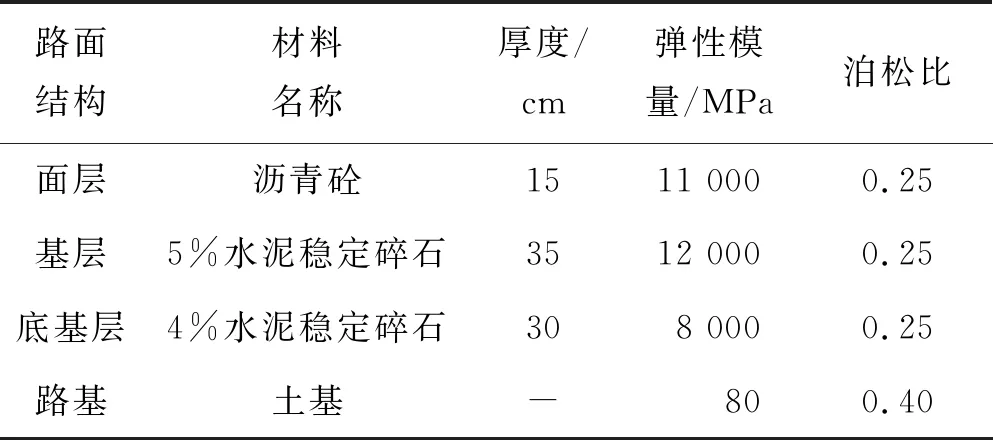
表2 典型路段的结构参数

(8)

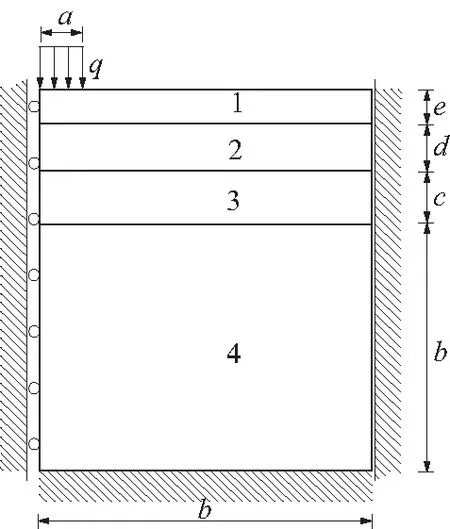
图4 多层轴对称模型

图5(a)表明随土基尺度的逐渐增大，弯沉值比较误差逐渐减小，与结构尺度为50 m×50 m的比较误差较大，当结构尺度达到15 m×15 m时比较误差超过10%；基层厚度越大，弯沉值比较误差越大。图5(b)表明以基层层底拉应力为控制指标时，土基尺度与基层层底拉应力成反比；基层厚度越大，结构尺度相同的情况下与理论值的相对误差越大。图5(c)表明以底基层层底拉应力为控制指标时，土基尺度与底基层层底拉应力成反比；底基层厚度越大，结构尺度相同的情况下与理论值的相对误差越大。与以基层层底拉应力指标相比，所得结论更趋于保守，即所取结构尺度更大。图5(d)表明以竖向压应力为控制指标时，土基尺度的变化与标准值的比较误差非常小，土基尺度为15 m×15 m时相对误差在0.4%以内，结构尺度的变化对其竖向力的影响很小。

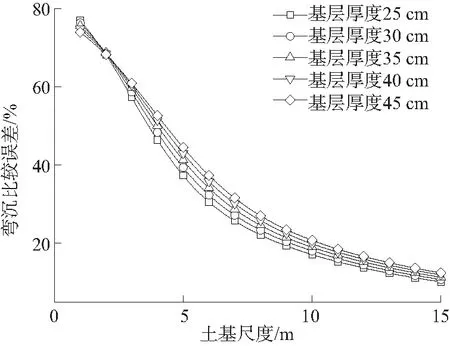
(a) 弯沉

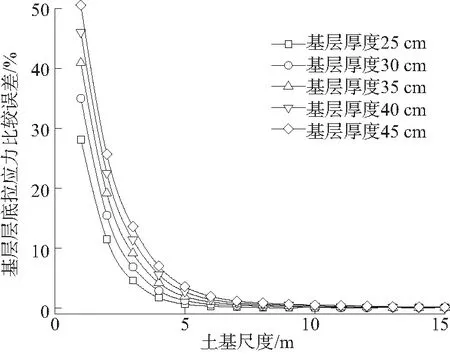
(b) 基层层底拉应力

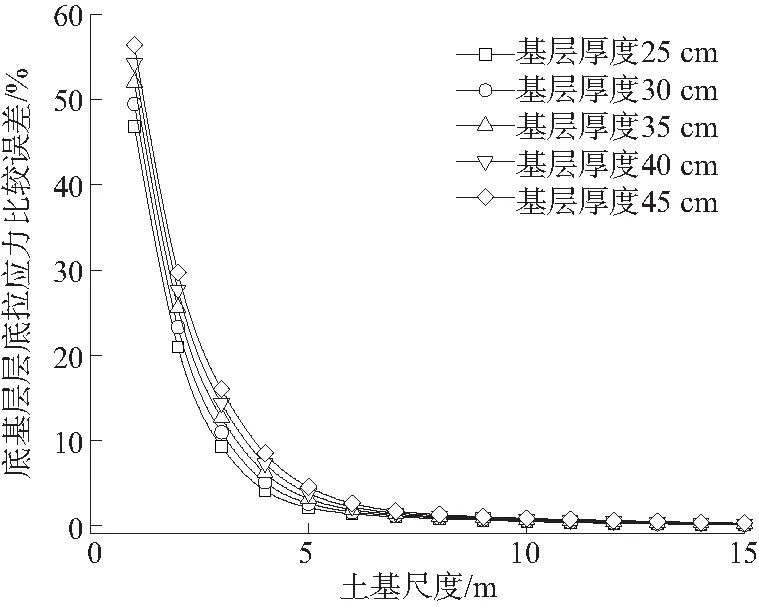
(c) 底基层层底拉应力

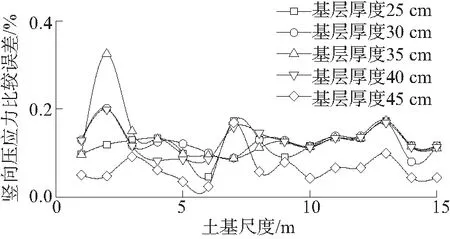
(d) 竖向压应力

由图5可知：当基层弹性模量一定时，基层厚度由25 cm变化为45 cm时，所取土基厚度与其相对误差成反比。基层厚度越大，与结构尺度为50 m×50 m的相对误差越大。以弯沉值为控制指标时，与标准尺寸相对误差确定的结构半空间尺度较大；以基层层底拉应力为控制指标时，f(3)=9.14%,f(4)=4.19%,f(5)=1.92%,f(6)=1.00%，根据土基尺度变化与50 m×50 m的相关关系及拉格朗日插值法，得出相对误差为1%的结构半空间尺度为6 m、相对误差为5%的结构半空间尺度为3.8 m；以底基层层底拉应力为控制指标时，f(4)=6.16%,f(5)=3.13%,f(6)=1.85%,f(7)=1.30%,f(8)=1.03%，得相对误差为1%的结构半空间尺度为8 m、相对误差为5%的结构半空间尺度为4.3 m。基层厚度越大，所取结构尺度应适当增大。王旭东认为对于半刚性基层和底基层，底基层的拉应力、拉应变略高于基层是符合一般规律的。马士宾等认为以弯沉为控制指标时，路面结构满足设计要求的概率最低；以层底弯拉应力和路基顶压应变为控制指标时，满足设计要求的概率较高。综上，考虑以底基层层底拉应力为控制指标，其相对误差为1%的结构尺度为8 m,相对误差为5%的结构尺度为4.3 m。

基层弹性模量与结构尺度的关系见表3。由表3可知：基层厚度为35 cm固定不变，基层模量的变化不会影响结构尺度与标准值比较误差的关系，比较误差几乎一致。使用基层层底拉应力、底基层层底拉应力和竖向应力为控制指标时，结论一致。结构尺度为8 m×8 m时的应力与位移见图6。

3 结论

(1) 由于模型及荷载的对称性，在轮载作用下的数值模拟计算结果呈对称分布。由于应力在传递时不断扩散，沿深度方向的应力值呈减小趋势。

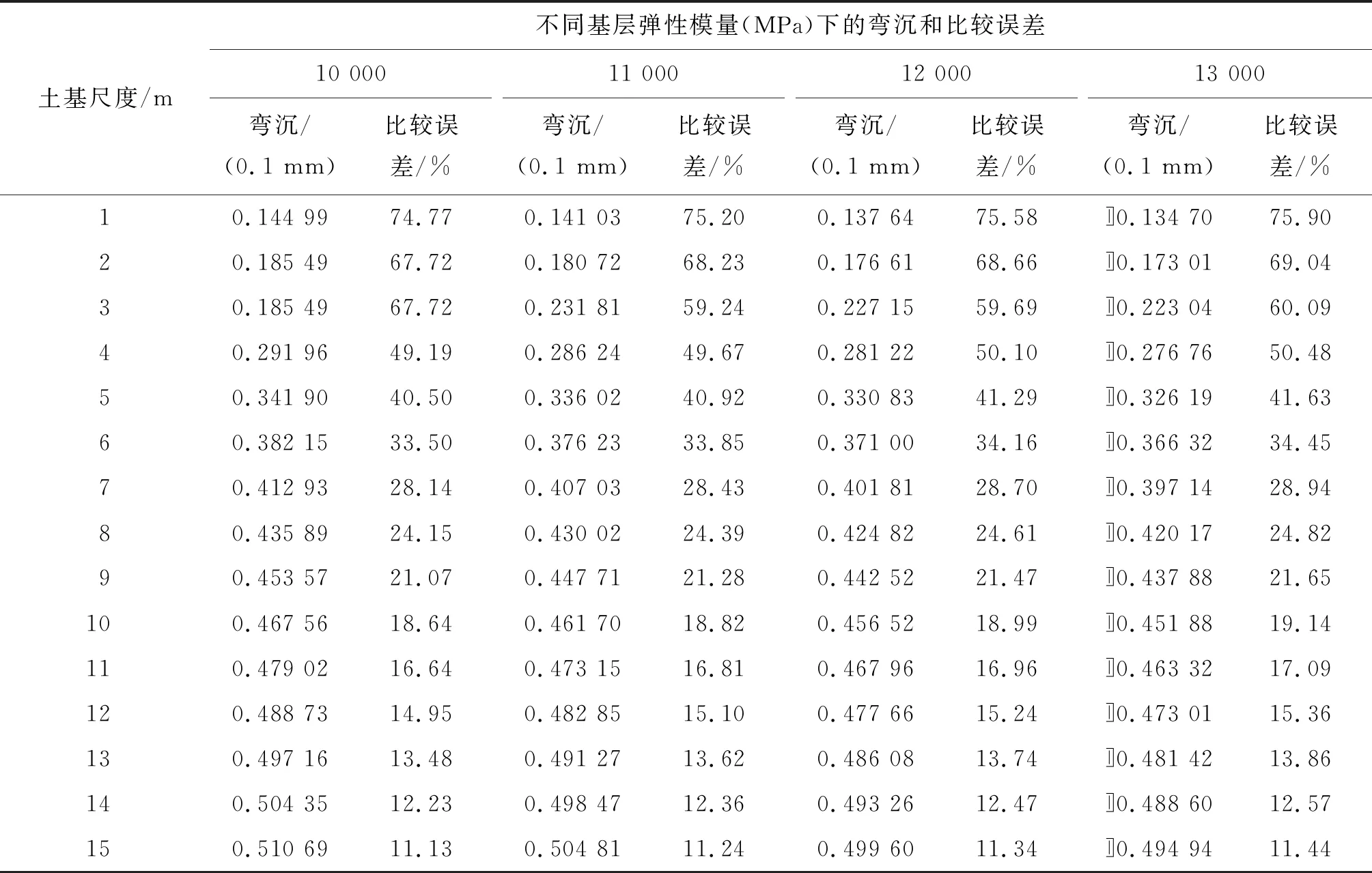
表3 基层弹性模量与结构尺度的关系

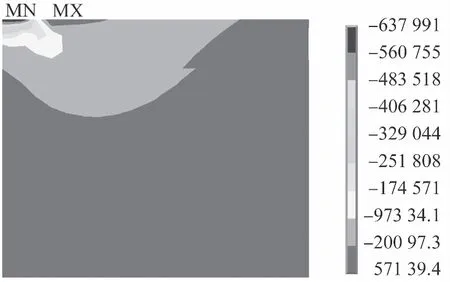
x方向

y方向

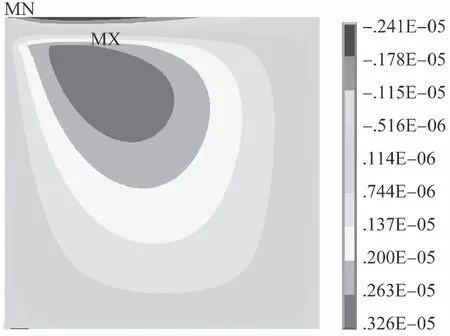
x方向

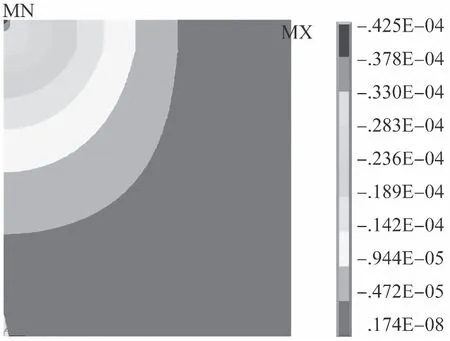
y方向

(2) 分析沥青路面结构精确尺度，根据有限元软件计算分析以弯沉值为控制指标的土基尺度时，最大误差为1%的土基尺度为8.7 m，最大误差为5%的土基尺度为1.8 m。

(3) 对于常见半刚性基层沥青路面结构，以弯沉值为控制指标时，与标准尺度相对误差确定的结构半空间尺度较大；以基层层底拉应力为控制指标时，相对误差为1%的结构半空间尺度为6 m，相对误差为5%的结构半空间尺度为3.8 m；以底基层层底拉应力为控制指标时，相对误差为1%的结构半空间尺度为8 m，相对误差为5%的结构半空间尺度为4.3 m。基层厚度越大，所取结构尺度比上述结论适当增大。以竖向压应力为控制指标确定的结构尺度与标准尺度相对误差很小。以底基层层底拉应力为控制指标更安全和精确。